基于Delaunay算法的子弹散布均匀性检验方法研究
2023-05-12宫会元宋艾平
宫会元,宋艾平
(63850部队,吉林 白城 137001)
0 引言
子弹药散布均匀性是子母弹重要的性能,是子母弹鉴定、验收等试验中必须考核验证的指标。现有子弹药地面散布均匀性评价方法主要有两种:一种是对散布区域分区并对各分区内落点数量分布应用统计方法进行检验;另一种是将落点按坐标方向分解,并按一维坐标分别检验均匀性。这些算法存在以下缺点:1)分组区间的划分方法主观性强,其合理性对检验结果有很大影响,降低了评价结果的可信度;2)只适用于样本数量足够大的情况;3)对不规则边界区域适应性差;4)忽略了分组区间内部均匀性等,制约了实际的应用。针对上述问题,文中引入Delaunay三角形剖分法,对子弹药落点散布均匀性进行研究,以解决现有方法的诸多缺点。
1 Delaunay三角剖分
三角剖分(triangulation)是计算几何领域中最主要的内容,是数值分析(有限元等)、信息可视化、计算机图形学等领域一项极为重要的预处理技术。Delaunay三角剖分由俄国数学家B.Delaunay于1934年提出,它是Voronoi 图的集合对偶图,具有严格的数学定义和完备的理论基础。Delaunay三角网因其具有优良的几何特性,如空外圆性质、最小角最大的性质等,是公认的最优三角网[1-2], 应用领域极为广泛,如:GIS、计算机仿真、地质学、计算机图形学及虚拟现实等。
1.1 Voronoi 图
定义1[1]:令d(x,Pi)表示x到Pi的欧式距离,则点Pi的邻域Vi定义为:
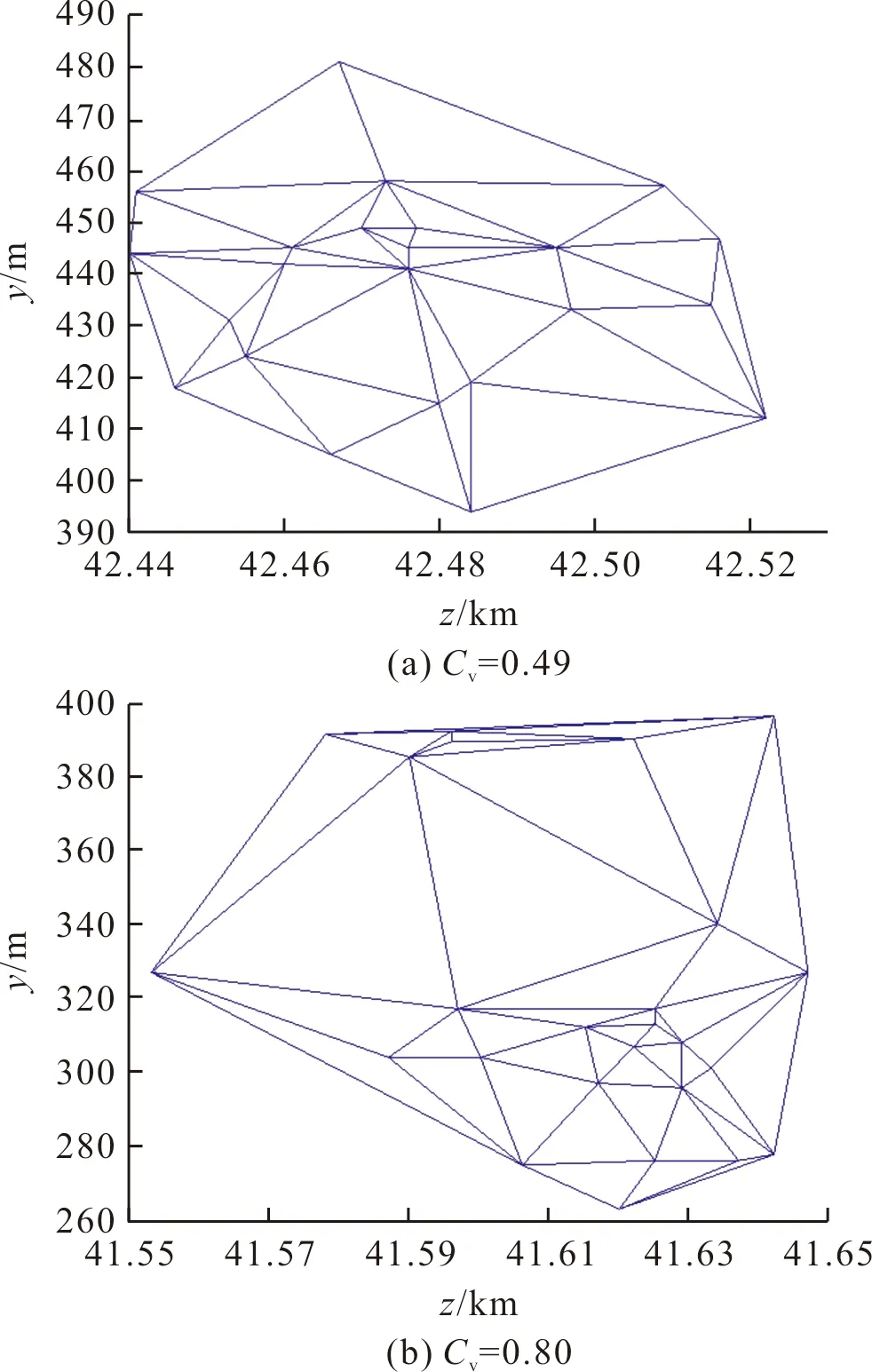
Vi={x∈Rn|d(x,Pi) (1) 式中:Rn为n维欧氏空间;i=1,2,…,n;j=1,2,…,n。 对于二维空间,Voronoi图如图1所示,图中阴影区域内的任意点到P2的距离近于到其他点Pi(i≠2)的距离,V1,V2,V3,V4,V5,V6确定的六边形称为P2的邻域,其边界对应于点P2的Voronoi多边形,它是由Pi与相邻点连线的垂直平分线围成的。二维Voronoi图是平面点集所有点的邻域多边形的并集。Voronoi多边形的数学期望为6[3] 图1 Voronoi图Fig.1 Voronoi ketch chart 定义2[1]:U为Ed空间的有限点集,点集U的Delaunay三角化定义为满足以下条件的单纯形单元复形D(U)[4]: 1)复形D(U)的0-单纯形组成的集合(即D(U)的所有顶点的集合)是U的子集。 2)复形的底空间是点集U的凸包C(U)。 3)任意一个d-单纯形ΔT∈D(U),|T|=k+1,满足:任意q∈U-T,q在ΔT的外接球外。 Delaunay三角剖分与Voronoi图为对偶图,Voronoi边(限有限长线段)的中垂线就是Delaunay边。如图2所示,虚线为Voronoi图,实线为Delaunay三角部分。 图2 Voronoi 图和Delaunay 三角剖分Fig.2 Voronoi ketch chart and Delaunay triangulation 单发子母弹的子弹药落点集合为P,其对应的二维区域为子弹药的落点散布区域。对散布区域进行Voronoi划分后,确定集合P中所有落点间的邻近关系,如图1中P2的邻近点为P1,P3,P4,P5,P6,P7。继续对点集P进行Delaunay三角剖分,剖分后的所有Delaunay边长构成的集合X,即为所有落点与其邻近点的距离的集合,其散布可以表征点集P在散布区域内分布的均匀性。 根据Delaunay三角剖分性质,一个点集的Delaunay三角剖分唯一确定,可以避免原有检验方法中对区域划分的主观性对结果带来的影响,提高了检验结果的可信性。且每个相邻点的距离均计入统计,能实现对全区域内的分布均匀性进行检验,杜绝了检验盲区。同时,该方法对样本数量无要求、对不规则边界区域适应性好。 以变异系数作为衡量各观测值离散程度的统计量,具有无量纲特性,不受计量单位和均值大小的影响,因此对于衡量不同弹药种类的相邻子弹间距离散布情况具有普适性。 若相邻子弹间距为x={x1,x2,…,xn},变异系数[2]Cv的表达式为: (2) 其中: (3) (4) 根据以上分析,建立均匀性检验步骤如图3所示。 图3 均匀性检验步骤Fig.3 Uniformity inspection steps 目前主流的Delaunay三角形剖分算法[5-9]有贪心算法、渐进插入算法、Tsung-pao Fang和Les.pieg算法,其中贪心算法的时间复杂度较高、渐进插入算法复杂度适中但对有约束情况适应性较差,Tsung-pao Fang和Les.pieg算法复杂度最低,但算法容易出现退化。因为子母弹外围区域处理方法采用凸多边形法,外围约束符合Delaunay剖分特点,因此选用计算复杂度较小的渐进插入算法。则均匀性检验算法步骤为: 1)输入m枚子弹坐标点集P,P={Pk|k=1,…,m};2)定义一个包含点集P的超三角形,把它作为初始Delaunay三角;3)将点集内一个未处理点Pk插入已有的Delaunay三角网内;4)在三角网中找出包含Pk的三角形,把Pk与这个三角形的3个顶点相连,生成3个新的三角形;5)应用Lawson提出的局部优化算法,向外更新该步之前生成的所有三角形;6)重复步骤3)~5),直到所有的点都被插入;7)删掉包含超三角顶点的所有三角形,完成三角形剖分;8)逐条计算Delaunay边长;9)计算变异系数及其散布;10)给定置信水平,判定子弹散布是否均匀。 若集合L内Delaunay边长均相等,即L1=L2=…=Lk,意味着此点集P的元素在分布区域内服从绝对的均匀分布,此时每3个相邻的落点均构成正三角形,此时变异系数Cv=0。 构造一组分布较为极端的数据,分布范围为100 m×80 m,子弹落点数量nm=90。所有数据分成3部分,每30个落点集中在一起,范围小于1 m×1 m,经计算,此时Cv=1.745。 由此可知,实际Cv值的变化范围为0~1.745。 设子弹落点散布半径为r,构造1 000组符合二维均匀分布的数据,分别取r,nm的组合为[40,28],[200,28],[200,200],[40,500], 基本覆盖常见子母弹数据范围,采用2.2方法对数据进行检验,得到各种条件下下对应的变异系数Cv值,结果如图5所示。经大量仿真结果显示,其均值对r,n不敏感,标准差随子弹数量增加有减小趋势。一般均匀分布条件下变异系数Cv均值约为0.567。 变异系数服从正态分布,即Cv~N(0.567,S2),且变异系数越小均匀性越好,若Cv≤Cv0,其中Cv0为阈值,则分布均匀。为进行均匀性检验作假设: 原假设:Cv>Cv0,备择假设:Cv≤Cv0 以坐标观测值为例,进行试验验证,典型计算Delaunay剖分结果如图4所示,给定显著性水平α=0.1,计算得Cv0=0.494,可判定当Cv=0.49时分布较均匀,当Cv=0.80时分布不均匀。 图4 子母弹典型Delaunay三角形剖分图Fig.4 Typical Delaunay triangulation of a certain type of submunition 由Delaunay三角形剖分图可见,变异系数随散布均匀性而单调变化,其值偏小时子弹散布相对均匀,偏大时存在局部聚集、散布区域内存在盲区的情况,根据变异系数能够直观判定均匀性。 基于Delaunay算法的子弹均匀性检验算法能够满足均匀性检验的唯一性、全局性、普适性要求,对子弹数量不敏感,避免了原有方法的不足,具有良好的可操作性。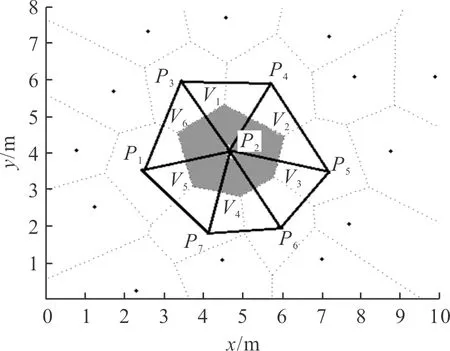
1.2 Delaunay 三角剖分
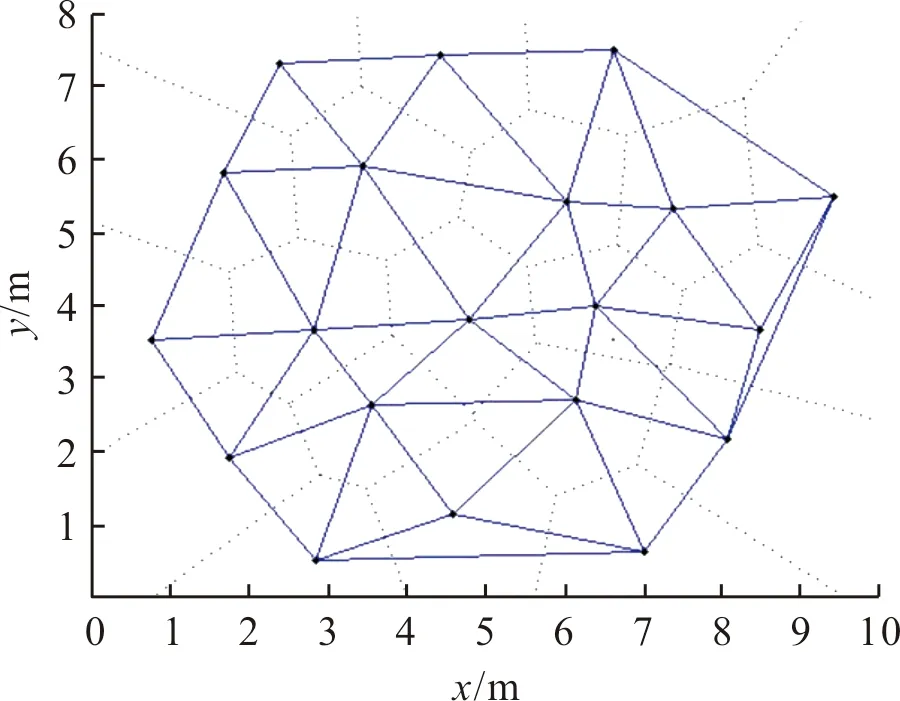
2 均匀性检验方法
2.1 检验模型

2.2 均匀性检验的算法实现
3 变异系数的仿真分析和阈值确定
3.1 变异系数理论分析
3.2 仿真分析
3.3 均匀性检验阈值
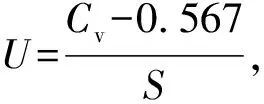
4 试验应用
5 结论
