基于速率匹配的FSO与RF间链路的动态切换算法

李春若，苑俊英

(1 江西财经职业学院信息中心，江西 南昌 331700；2 广州南方学院电气与计算机工程学院，广东 广州 510970)

0 引言

卫星通信能够为地面固定、移动用户提供宽带接入和无缝连接[1-2],已经在战场、5G通信以及海上航行等领域广泛使用。尽管卫星通信覆盖范围广,但是当卫星与地面用户间有建筑物或障碍物时,就可能存在覆盖盲区,这就降低了通信质量,延长了通信时延[3]。

作为一种新型空中通信载体,高空平台(high-altitude platform, HAP)兼具机动性和广域覆盖特点。通常HAP有基于气球、无人机(unmanned aerial vehicle, UAV)等形式,并能够根据目标区域特点选择合适的平台形式[4]。实质上,HAP通信是指在平流层中,以无人机或者气球等驻空平台作为无线中继或空中基站,为地面用户提供覆盖的通信系统。在基于HAP协助的卫星通信中,通过部署多个HAP扩大覆盖区域[5]。

此外,因机动性好,UAV作为低空基站[6-7]提高了对地面用户的覆盖性能。基于UAV的空中基站已在工业领域、智慧农业等领域内广泛使用。

文中考虑卫星、平台和无人机的S-HAP-UAV的两跳星地融合网络,其中HAP作为卫星与UAV间的转发节点。这就形成两条链路:卫星至HAP(S-H)和HAP至UAV(H-U)。由于HAP位于平流层,S-H链路易受大气湍流、云层影响。因此,S-H链路采用自由空间光通信(free space optical, FSO)[7]链路。

在H-U链路中,FSO链路可能也受天气因素影响,如云层、雪、大气湍流,这些因素降低了链路的可靠性。此外,一个HAP能为多个UAV提供服务。然而,由于UAV移动以及波束失调,光链路容易中断。为此,选用RF链路作为备用链路。即针对H-U链路,优先考虑FSO链路。若光信道条件不能维持高速率,则选用RF链路。

为此,针对基于HAP转发的两跳星地融合网络,提出基于速率匹配的FSO/RF链路的动态切换算法(rate adaptation-based free space optical and RF dynamic switching,RADS)。RADS算法依据信道状态信息,动态决策在HAP至UAV间是采用FSO,还是RF链路,进而提升数据的传输速率。仿真结果表明,提出的RADS算法可有效提升平均速率,降低链路的中断概率。

1 系统模型

1.1 网络模型

考虑基于HAP转发的两跳星地融合网络,如图1所示。

图1 网络模型Fig.1 Network model

卫星为源节点,HAP为转发节点,UAV为目标节点,其中Hs,Hh和Hu分别表示卫星、HAP和UAV的高度。源节点采用正交调幅(quadrature amplitude modulation, QAM)调制[8],输出的电信号为[8]:

sn(t)=AnIg(t)cos(2πfrt)-AnQg(t)sin(2πfrt)

(1)

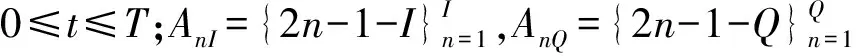
利用电信号sn(t)调制光束的强度,形成已调光信号[7]:

s(t)=Pt[1+msn(t)]

(2)

式中:Pt为卫星的传输功率;m为调制系数。

1.2 HAP端的输出信号

HAP端利用光学孔径收集光信号,然后将光信号传输至光交换机。HAP依据信道状态信息(channel state information, CSI)[9]决定采用FSO链路或RF链路。若选择RF链路,就需将光信号转换成电信号,再传输至UAV。若是RF链路,HAP端输出的电信号为[9]:

rr(t)=GRF[ηhSRPtmsn(t)+ηnb1+nre_hap]

(3)

式中:η为光-电转换效率;hSR为S-H链路中光束传播损耗;nb1为背景端噪声;nre_hap为接收端噪声;GRF为电子放大器增益;GR为光放大器增益。

若是FSO链路,HAP端输出的光信号为[9]:

rf(t)=GF[hSRs(t)+nb1]

(4)

1.3 UAV端接收的信号

通过RF链路,UAV端接收的信号为:

yr(t)=hRFGRFηhSRPtmsn(t)+hRFGRFηnb1+
hRFGRFηnre_hap+nre

(5)

通过FSO链路,UAV端接收的信号为:

yf(t)=hFSOGFhSRPtmsn(t)+hFSOGFηnb1+ηnb2+nrec

(6)

式中:hRF和hFSO分别为RF链路和FSO链路的信道增益系数;nre和nrec分别为RF链路和FSO链路的接收端噪声。

1.4 UAV端信号的信噪比

从源节点(卫星)至目的节点(UAV)有两条路径。这两条路径的第一跳链路相同,即基于FSO的卫星至HAP链路;第二跳链路不同,即HAP至UAV。为了简化表述,用FSO-FSO表示第一跳链路;用FSO-RF表示第二跳链路。

(7)

(8)

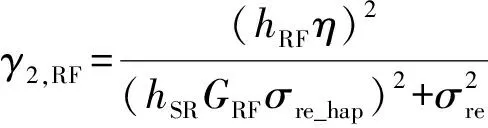
2 RADS算法

2.1 RADS算法概述

RADS算法旨在满足预定服务质量基础上,最大化无线信道的速率。为了实现RF/FSO链路的动态切换,UAV端安装了信道检测器,如图2所示。通过信道检测器估计FSO链路和RF链路的信道状态信息CSI。CSI反映了关于数据传输率和链路的信息。

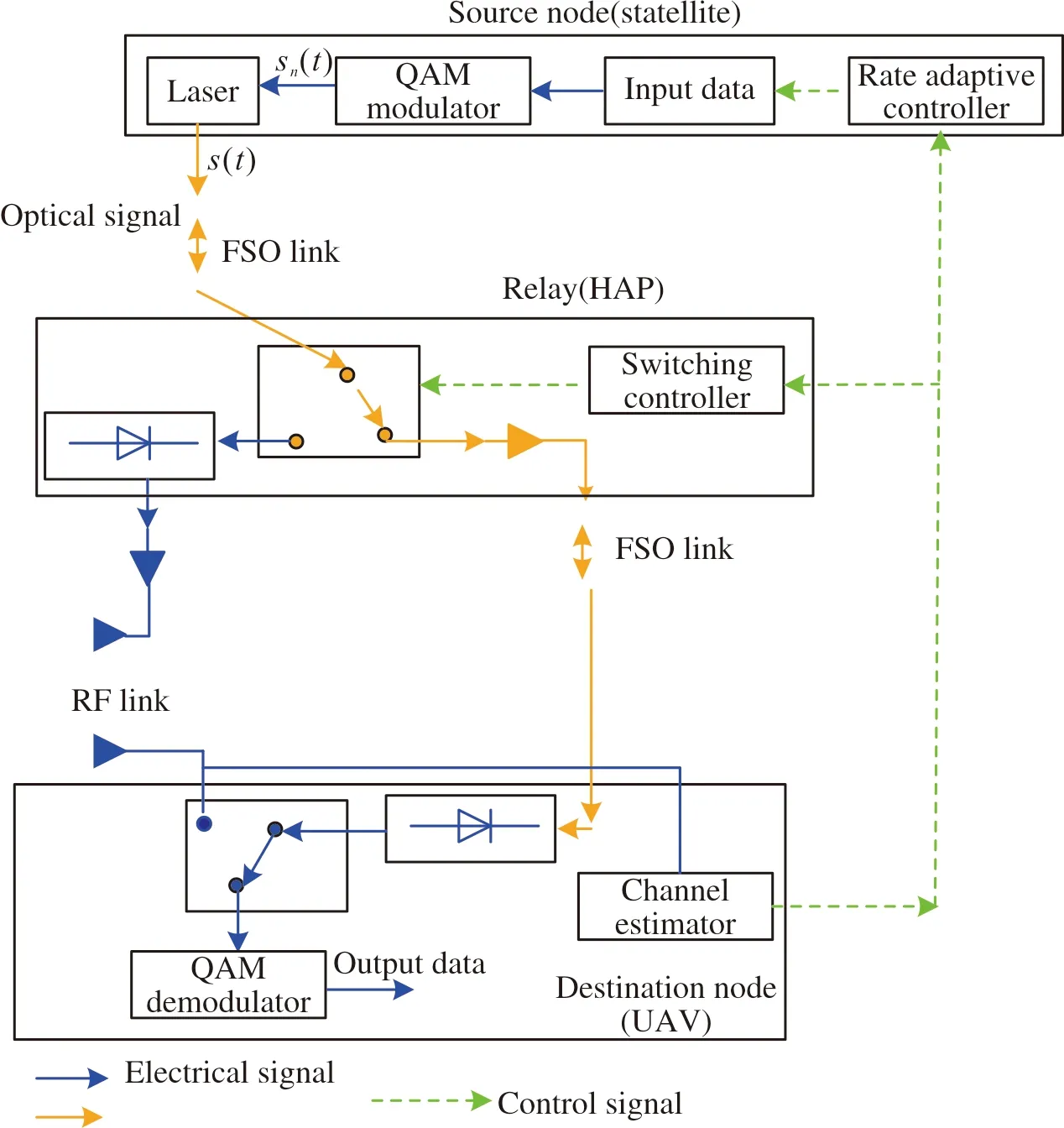
图2 RADS算法框架Fig.2 Framework of RADS algorithm

由于FSO链路的传输速率高于RF链路传输速率,RADS算法在第二跳链路中优先采用FSO链路。只有当FSO链路不能满足速率要求时,才选用RF链路。

2.2 基于M-QAM调制的FSO链路的动态速率

FSO链路采用子载波的M进制的QAM(M-QAM)。FSO链路具有m个可能的传输模式,其固定速率为Rf。为了能以动态速率传输数据,将接收信号的SNR划分为(m+1)个不重叠的间隔:

(9)

(10)

式中:E0表示允许的最低误码率。

(11)

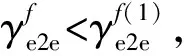
2.3 基于N-QAM调制的RF链路的动态速率

RF链路采用子载波的N进制的QAM(N-QAM)。RF链路具有n个可能的传输模式,其固定速率为Rr。为了能以动态速率传输数据,将接收信号的SNR划分为(n+1)个不重叠的间隔:

(12)

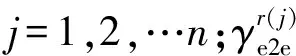
(13)

(14)

3 性能仿真

3.1 仿真环境

利用MATLAB软件建立仿真平台,分析RADS算法的性能。选择3类策略作为基准算法,对比分析RADS算法的性能:1)自适应速率的两跳FSO-FSO算法(ADFF); 2) 自适应速率的两跳FSO-RF算法(ADFR); 3)传统的固定速率的FSO-FSO/RF算法(FFFR)。表1给出RADS算法、ADFF算法、ADFR算法和FFFR算法的区别。

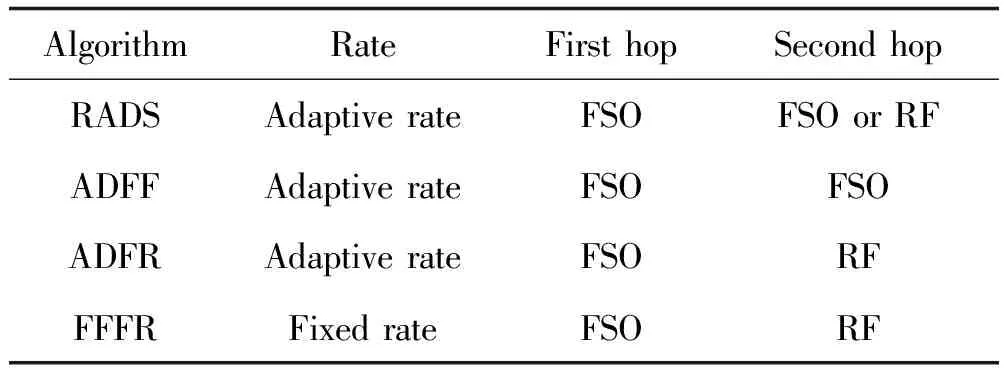
表1 基准算法的不同Table 1 Difference of baseline algorithms

此外,在仿真过程中,自适应速率算法的FSO链路采用M-QAM调制,其中M∈[2,4,8,16,32,64,128];RF链路采用N-QAM调制,其中N∈[2,4,8,16,32]。而固定速率算法(FFFR算法)中FSO链路和RF链路均采用32-QAM。仿真参数如表2所示。

表2 仿真参数Table 2 Simulation parameter

3.2 两跳链路的中断性能

分析卫星传输功率和云层中云水量(cloud liquid water content, CLWC)对两跳链路的中断性能的影响。如图3所示,其中c表示云层中云水量。此外,图中的FFFR-1/2表示文献[12]采用的算法。该算法采用ADFF策略,但为BPSK调制,且编码率为1/2。

图3 中断性能Fig.3 Outage probability

从图3可知,CLWC对中断概率性能有重要影响。CLWC的增加,极大降低了ADFR算法的中断概率,即使FFFR-1/2算法采用了编码策略,其中断概率仍较大。而ADFR算法的中断概率几乎不受CLWC影响,原因在于:云层对FSO链路影响更大。此外,在c=6 mg/m3,卫星传输功率较大(20 dBm)时,FFFR算法的中断性能优于ADFR。

其次,无论CLWC处于何种情况,相比于ADFR和FFFR算法,RADS算法的中断概率均较低,这归功于:RADS算法充分发挥了FSO和RF链路的优势。

3.3 平均数据传输速率

分析RADS算法与FFFR算法的平均数据传输速率,即比较自适应速率与固定速率两种方式对数据传输的平均速率的影响。图4给出RADS算法和FFFR算法的平均数据传输速率,其中卫星传输功率为15 dBm,CLWC变化范围c为2～10 mg/m3。

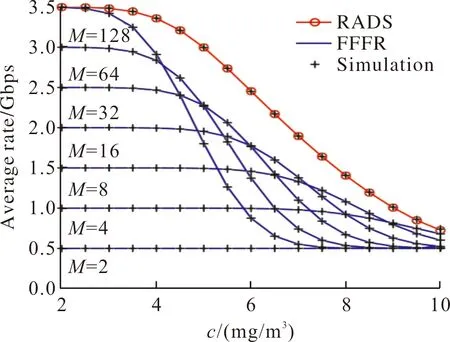
图4 平均传输速率Fig.4 Average transmit rate

从图4可知,相比于FFFR算法,RADS算法能够获取高的平均传输速率。原因在于:1)在云层影响较低(CLWC较小)时,高阶调制系统能够获取高的速率;2)在云层影响较高(CLWC较大)时,高阶调制系统容易受CLWC影响。因此,采用固定速率的FFFR算法并不适应于变化的信道,而自适应选择速率是更好的选择。例如,当c=6 mg/m3时,RADS算法能够获取2.45 Gbps的平均速率,而FFFR算法只能获取1.77 Gbps的平均速率。

3.4 频谱利用率

分析RADS算法和FFFR算法的频谱利用率,如图5所示,其中c=6 mg/m3。从图可知,RADS算法的频谱利用率优于FFFR算法。例如,当卫星传输功率为20 dBm时,RADS算法的频谱利用率达到6.8 bit/symbol,而FFFR算法在128-QAM,64-QAM,32-QAM,16-QAM,8-QAM,4-QAM和2-QAM调制下可获取的频谱利用率分别为6.2 bit/symbol,5.8 bit/symbol,4.9 bit/symbol,4 bit/symbol,3 bit/symbol,2 bit/symbol,1 bit/symbol。

图5 频谱利用率Fig.5 Spectrum efficiency

3.5 平均误码率

分析RADS算法和FFFR算法的平均误码率。如图6所示,其中卫星传输功率为20 dBm,c=6 mg/m3,θHAP为发散角。

图6 平均误码率与平均传输速率Fig.6 Average bit error rate and average transmit rate

从图6可知,相比于FFFR算法,RADS算法降低了误码率,这符合预期。原因在于:设计RADS算法的目的就是在满足最低误码率情况下最大化速率。此外,由图6可知,合理选择θHAP可降低误码率。

4 总结

为提高从HAP至UAV的下行链路的速率,提出基于速率匹配的FSO/RF链路的动态切换算法RADS。RADS算法优先使用FSO链路。当从FSO链路接收的SNR低于阈值,就切换至RF链路,并依据信号的SNR值,动态调整传输模式,进而提高系统速率。仿真结果表明,相比于固定速率算法,提出的RADS算法降低了系统的中断概率,并提高了速率。

从链路切换角度提升系统性能,但未涉及传输功率的优化问题。而传输功率对提升网络能效有重要影响。研究如何优化传输功率,进而提升网络能效,这将是后期的研究工作。