建立体积表象 发展空间观念
2023-05-12孙齐圣
孙齐圣


《长方体和正方体的体积》是人教版数学五年级下册第三单元的教学内容。本课时是在学生掌握长方体、正方体特征的基础上教学的,目的是让学生通过动手操作、自主探索,提炼出长方体、正方体的体积计算公式,并通过应用公式,进一步深化对体积公式的理解,从而建立体积观念、发展空间想象力。
一、在拼摆活动中感悟公式原理
体积计算公式的推导基于对体积概念的理解。在之前的学习中,学生对体积和体积单位已经有所认知,能够通过数体积单位的个数来求长方体的体积。基于此,笔者通过猜测、拼摆、比较、归纳等活动,引导学生感悟长方体体积计算公式的原理。
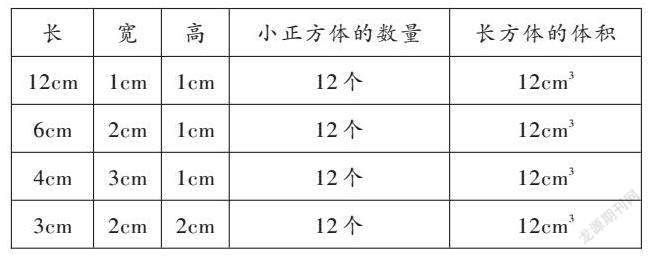
上课伊始,笔者先提出问题:怎样知道一个长方体或一个正方体的体积?长方体、正方体的体积与什么有关?学生根据自己的知识、经验猜想:把长方体切成若干大小相同的小正方体,再数小正方体的个数,就能知道长方体的体积;先测量长方体的长、宽、高,再算出体积;长方体的体积可能与长方体的长、宽、高有关;等等。接着,笔者组织学生在组内用12个体积为1cm3的小正方体摆出不同的长方体,并将每次摆好的长方体的相关数据填入教材第29页的表格中。学生自主拼摆后,笔者用课件呈现下表。
笔者引导学生观察表格并设疑:“这些长方体有什么共同点和不同点?”一名学生回答:“这些长方体的长、宽、高不同,即长方体的形状不同,但它们所需的小正方体的数量也就是长方体的体积是相同的。”笔者继续设疑:“根据拼摆过程想一想,长方体长、宽、高的数值除了表示长方体的长、宽、高的长度,还表示什么?”另一名学生回答:“还可以表示摆成长方体的每行小正方体的个数、摆的行数和层数。”
然后,笔者引导学生分享、交流摆成的不同长方体的各项数据。第一小组代表回答:“我发现每行摆的个数、摆的行数、摆的层数分别与摆成的长方体的长、宽、高的数值相同。”第二小组代表回答:“我发现摆成的长方体所包含体积单位的数量就是长方体的体积。”第三小组代表补充道:“摆成的长方体所含体积单位的数量就是每行摆的个数(长)、摆的行数(宽)、摆的层数(高)的乘积。”笔者顺势用课件呈现“长方体的体积=长×宽×高”。最后,笔者引导:“如果用字母V表示长方体的体积,用a、b、h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以怎样表示?”学生回答:“可以写成V=abh。”
通过拼摆,学生找出了长方体所含体积单位的数量与它的长、宽、高之间的关系,感悟到长方体体积计算公式的原理。
二、在推理过程中理解公式本质
正方体可以看成是长、宽、高都相等的长方体,即正方体是特殊的长方体。为了让学生弄清长方体和正方体的关系,笔者立足学生已有的认知经验,引导学生经历计算、分析、推理、归纳的过程,帮助学生理解正方体体积的本质。
教学时,笔者先呈现例1的第①小题:“一个长方体长7cm、宽3cm、高4cm。求这个长方体的体积。”学生根据长方体体积计算公式列式计算:V=abh=7×3×4=84cm3。笔者设疑:“如果把长方体的长缩短3cm、宽增加1cm,此时的长、宽、高各是多少?长方体变成了什么图形?”一名学生回答:“此时长方体的长、宽、高都是4cm,长方体变成了一个正方体。”笔者追问:“怎样计算这个正方体的体积呢?”他接着回答:“根据V=abh可知,正方体体积用‘(7-3)×(3+1)×4计算,即4×4×4=64cm3。”“我们刚才利用长方体体积的计算公式求出了正方体的体积,谁能说说正方体的体积怎样计算?”笔者继续设疑。另一名学生回答:“可以按照长方体体积的计算公式‘V=abh来计算。因为正方体是长、宽、高相等的特殊长方体,所以长方体体积的计算公式也适用于正方体。”笔者顺势总结:“正方体的‘长、宽、高,我们统称为‘棱长,如果用字母V表示正方体的体积,用a表示它的棱长,那么正方体的体积计算公式用字母怎样表示?”学生立即答出:“正方体体积V=a×a×a=a3。”
经历了推理过程,学生不仅理解了正方体体积的计算方法,而且完善了认识结构。
三、在直观观察中深化体积公式
在学生整体建构长方体、正方体体积的认知结构的基础上,笔者借助直观图示,利用从实际操作到简化操作再到想象操作的过程,引导学生自主发现规律,深化对长方体、正方体体积计算公式的理解,更好地建立空间观念。
教学时,笔者先呈现下图,引导学生通过对比观察发现:无论两个图形怎么摆放,总有一个面是朝下的。笔者顺势总结:这个面被称为底面,长方体或正方体底面的面积叫作底面积。
接着,笔者设疑:“长方体和正方体的底面积该怎样计算呢?”一名学生观察后回答:“长方体的底面积=长×宽,正方体的底面积=棱长×棱长。”笔者在相应的体积公式上做了如下标记:
然后,笔者总结:“长方体体积公式中的‘长×宽就是它的底面积,则其体积公式可写成‘底面积×高;正方体体积公式中的‘棱长×棱长就是它的底面积,而另一条棱长也可以看作是正方体的高。”“这样看,长方体和正方体的体积可以怎样计算?”笔者设疑。学生回答出“长方体(或正方体)的体积=底面积×高”后,笔者引导学生用字母表示长方体(或正方体)的体积公式,即“V=Sh”。
为了引导学生突破定式,理解底面积的本质,笔者呈现下图,让学生观察:“图中涂色面的面积能看作长方体的底面積吗?为什么?”
一名学生回答:“能。如果把长方体‘立起来,涂色的面就朝下了,所以涂色的面可以看作长方体的底面积。”笔者追问:“此时长方体可以看成是底面积、高各是多少的长方体?”他继续说:“可以看成底面积是‘10×4=40、高是6的长方体。”笔者继续设疑:“还可以看成怎样的长方体?”另一名学生回答:“还可以看成底面积是‘6×4=24、高是10的长方体,也可以看成底面积是‘10×6=60、高是4的长方体。”笔者总结:长方体(或正方体)的体积可以用某一个面的面积与垂直于这个面的棱的长度相乘的方法来计算。
学生经历了观察、比较、归纳的过程,进一步理解了长方体和正方体的体积公式之间的内在联系,为今后学习其他柱体的体积计算公式做了铺垫。
(作者单位:应城市四里棚中心学校)
责任编辑 张敏
