基于改进ORB的无人机影像拼接算法
2023-05-11何显辉
张 平,孙 林,何显辉
(山东科技大学 测绘与空间信息学院,山东 青岛 266590)
0 引言
近年来,无人机航拍摄影技术越来越成熟,在遥感监测[1]、电力巡检[2]、灾害勘察[3]、军事侦察[4]等领域均有广泛应用。无人机航拍影像具有像幅小、影像数量多的特点,而单幅影像中所包含的信息有限,通常需要对无人机航拍影像进行拼接以构建高分辨率的全景影像,因此研究快速准确拼接高质量无人机影像的算法具有十分重要的现实意义[5-6]。
图像拼接流程主要分为预处理、图像配准和图像融合3 个部分,其中图像预处理是对图像进行去噪等;图像配准为计算变换矩阵,对图像进行变换;图像融合是利用融合算法消除图像拼接痕迹。图像配准是图像拼接的前提条件,图像拼接的质量取决于配准精度。基于特征的图像配准算法是当前主流,通过提取局部鲁棒特征进行配准具有抗干扰性强、稳定性高等特点。例如,Lowe[7]提出SIFT(Scale-invariant Feature Transform)算法,在图像配准方面展现出优异性能,但由于特征维数高,导致配准时间长;针对SIFT 算法存在的问题,Bay 等[8]提出SURF(Speeded Up Robust Features)算法,降低了特征描述符维数,兼顾配准速度与精度,但仍然不能满足实时性要求;Rublee 等[9]提出ORB(Oriented FAST and Rotated BRIEF)算法,该算法的图像配准速度远超SIFT 和SURF 算法,满足实时性要求,但配准精度有所下降;王艳等[10]针对SIFT 算法配准耗时长的问题,利用遗传算法对SIFT 算法配准过程进行优化,极大降低了配准时间;陈伟等[11]采用FAST(Features from Accelerated Segment Test)算法进行特征点检测,并利用自适应最近邻比值提高配准精度,然后通过随机采样一致性(Random Sample Consensus,RANSAC)算法计算单应性矩阵,有效提升了匹配效率;刘天赐等[12]采用渐进采样一致性(Progressive Sample Consensus,PROSAC)算法对ORB 算法进行匹配优化,有效降低了匹配时间与均方根误差,提高了拼接图像质量。
在以上研究基础上,本文提出一种基于改进ORB 的无人机遥感影像拼接算法。该算法在特征检测阶段构建尺度金字塔,利用ORB 算法提取特征点以构建特征点尺度不变性;然后利用BEBLID(Boosted Efficient Binary Local Image Descriptor)描述符[13]代替ORB 算法中的BRIEF(Binary Robust Independent Elementary Features)描述符[14]对特征点进行描述,利用最邻近距离比值(Nearest Neighbour Distance Ratio,NNDR)匹配策略和最优化几何约束对误匹配点进行剔除,获取高质量特征点集,进而计算得到更加精确的变换矩阵;最后使用改进的渐入渐出算法进行图像融合,降低图像重叠区域重影的影响,以获取高质量拼接图像。
1 特征检测
1.1 多尺度FAST特征检测
ORB 算法在特征点检测阶段利用FAST 算法提取图像特征点。如图1 所示,FAST 算法对待检测像素点圆形候选区域中的16 个像素点进行比较,如果候选区域中存在一组连续n 个像素,且像素亮度值均高于或低于待检测像素亮度值与设定阈值之和,则定义该像素点为特征点[15]。为提升FAST 算法的检测效率,设定截止条件检测图1 中像素p 邻域上1、5、9、13 四个位置上的像素,若其中3 个像素满足检测条件,则继续检测;反之,则当前检测点不是特征点。
FAST 算法具有检测速度快、精度高的特点,但其仅在单一尺度检测,特征点不具有尺度不变性。本文通过构建图像金字塔,在不同尺度图像上利用FAST 算法进行特征检测,实现了特征尺度不变性。

Fig.1 FAST pixel sampling location图1 FAST像素点采样位置
1.2 BEBLID特征描述
在利用多尺度FAST 算法检测特征点时,为了对特征点进行局部表述,必须对特征点局部鲁棒结构进行描述,本文采用BEBLID 描述符对特征点进行描述。BEBLID 描述符是一种高效的二进制描述符,通过选取最具有分辨力的采样对特征组合构建描述符,具有计算复杂度低、配准速度快、精度高的特点[16]。
如图2 所示,BEBLID 描述符是在特征点邻域内选取n对不同尺寸比例S 的正方形区域作为采样对,计算采样对平均灰度值之间的差异,并与设定阈值T 比较,将小于T 的采样对设为1,大于T 的采样对设为-1,然后利用BoostedSSC 算法对特征进行区分,选取前K 个特征进行组合,将大于阈值的特征输出为0,小于阈值的采样对输出1 以构建二进制描述符。
Fig.2 Distribution of position and spatial weight of feature sampling pair图2 特征采样对位置及空间权重分布
2 特征匹配及优化
采用BEBLID 二进制描述符对局部特征进行描述,利用汉明距离进行配准。直接对特征点进行暴力匹配会产生大量误匹配,因此本文首先采用NNDR 匹配策略对特征点进行粗配准,然后通过最优化几何约束对匹配点对进行优化。
2.1 NNDR算法
NNDR 算法保留了待配准图像中与参考图像特征描述点距离最近和次近的特征点,通过计算最近距离与次近距离的比值对特征点进行约束[17]。计算公式为:
式中,Dnn和Dnr分别为最近和次近邻特征点的汉明距离;TD为设定阈值,一般为0.8。
2.2 最优化几何约束
根据粗匹配中特征点对的最邻近比值升序排列,在前n 对匹配特征点中随机选取3 对特征点进行投票,选取具有最佳适应度的3 对特征点对建立局部坐标系,利用构建的局部坐标系对特征点进行向量坐标表示,计算向量坐标在局部坐标系中的坐标相似度,将相似度低于阈值的匹配点对予以剔除。
选取前n对特征点构成集合R={(Mi,Ni)|i=1,···,n},其中Mi和Ni为一对匹配特征点。从集合R中随机选择3 个特征点,通过式(2)计算特征点在局部坐标系中的相似度。
式中,Sim(Mj,Nj)表示R中其余特征点在当前局部坐标系中的相似度;{(Dji,Dji′)|i=1,2,3}为匹配点对Mj和Nj到3个匹配特征点的欧式距离。
从集合R 中随机选择3 个点构建局部坐标系,其余特征点对这个局部坐标系进行投票,选择得分最高的3 个点构建的坐标系作为最优坐标系[18]。Score表示当前3 个特征点构建的局部坐标系的投票得分,表示为:
局部坐标系构建示意图如图3所示。
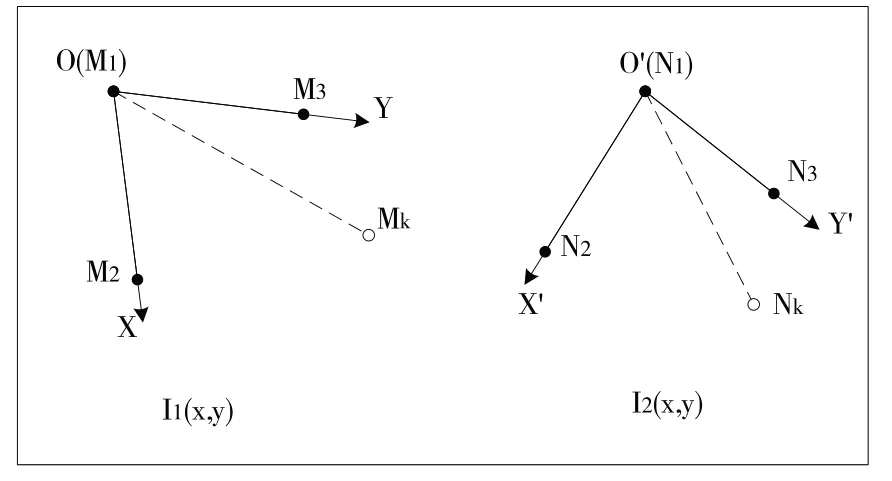
Fig.3 Schematic diagram of local coordinate calculation of linear primitives图3 局部坐标系构建示意图
在最优坐标系中以向量形式表示特征点,通过式(4)计算向量坐标的坐标相似度:
式中,PM和PN为局部坐标系特征点的坐标。比较坐标相似度S与设定阈值,若S小于阈值,则剔除该对特征点。
2.3 变换矩阵求解
对初始特征点进行粗匹配和最优化几何约束后得到配准图像高质量匹配特征点对,计算匹配点对之间的变换关系,利用RANSAC 算法对特征点对进行单应性矩阵估计获取最优变换矩阵,通过最优变换矩阵对图像进行变换。
3 图像融合
3.1 渐入渐出加权融合
在图像拼接过程中,由于无人机拍摄角度以及外界环境变化造成重叠区域的灰度差异,在对重叠区域进行图像融合时会出现模糊重影以及拼接缝隙等情况[19-20]。为消除图像拼接痕迹,通常采用渐入渐出加权融合算法[21]对图像进行融合。算法表达式为:
3.2 算法流程
本文算法流程如图4 所示,具体为:①对输入的配准图像进行多尺度FAST 特征点检测,并利用BEBLID 描述符对特征点进行特征描述;②采用NNDR 算法进行粗匹配;③基于特征点投票构建最优化几何约束对特征点进一步优化;④利用RANSAC 算法计算变换矩阵,获取高精度变换矩阵;⑤利用改进的渐入渐出加权融合算法实现图像拼接。
4 实验方法与结果分析
实验平台环境配置为Intel Core i7-10750H 处理器,16G 内存,使用C++编程语言对算法进行实现。选取如图5 所示的两组无人机图像进行拼接,比较SURF+NNDR+RASANC+渐入渐出算法(以下简称SURF)、ORB+NNDR+RASANC+渐入渐出算法(以下简称ORB)与本文算法在图像配准精度、拼接实时性以及拼接图像质量3 个方面的表现,对算法性能进行评估。

Fig.4 Algorithm flow图4 算法流程

Fig.5 Experimental image图5 实验图像
4.1 图像配准精度比较
在配准精度比较实验中,由于无人机航拍影像之间缺乏正确变换矩阵数据,无法对配准精度进行有效验证,因此选取经典Mikolajczyk 匹配数据集中具有旋转视角变换的Bark 图像、旋转变换的Boat 图像和光照变化的Leuven图像3 个图像序列进行实验,通过匹配正确度、正确特征点对的均方根误差两个指标评估算法配准性能。
表1 为3 种算法配准精度的比较结果,序列中的Image1 为基准图像,Image2-6 用于与其配准。可以看出,在对具有旋转视角变换的Bark 图像序列配准中,SURF 算法配准精度最佳,ORB 算法配准精度低于SURF 算法与本文算法,本文算法虽然在Image6 配准时失败,但配准成功的Image2-5 的配准精度均高于其他两种算法;在Boat 图像序列配准实验中,3 种算法均取得了较好的配准效果,其中ORB 算法的配准精度高于SURF 算法,但低于本文算法,本文算法配准精度比ORB 算法提高了0.77%,比SURF 算法提高了8.09%;在具有光照变化的Leuven 序列图像配准实验中,本文算法取得了取得100%的最佳配准精度,配准效果优异,比SURF 算法提高了0.82%、比ORB 算法提高了3.43%。通过分析3 个实验,本文算法在小尺度的旋转视角变换实验中配准精度较高,但在旋转视角变换尺度较大时会出现配准失败的情况;在光照变化和旋转变换实验中均取得了最佳配准精度,说明本文算法具有良好的光照不变性和旋转不变性。综上所述,本文算法对不同特性的影像均具有较好的配准效果。

Table 1 Comparison of registration accuracy of different algorithms 表1 不同算法配准精度比较 (%)
表2 为配准实验中3 种算法正确匹配点的均方根误差。在Bark 和Boat 图像序列中,本文算法的均方根误差均为最小;在Leuven 图像中,本文算法均方根误差虽略大于SURF 算法,但小于1,且低于ORB 算法。
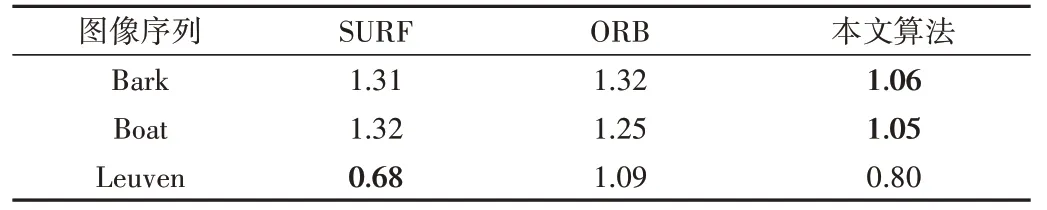
Table 2 Comparison of root mean square errors of different algorithms表2 不同算法均方根误差比较
4.2 图像拼接实时性比较
表3 为3 种算法对两组实验图像的拼接时间比较。本文算法和ORB 算法均采用二进制描述符和汉明距离配准,配准时间复杂度低,拼接时间远低于SURF 算法;且本文算法拼接时间略低于ORB 算法,图像拼接速度最快。
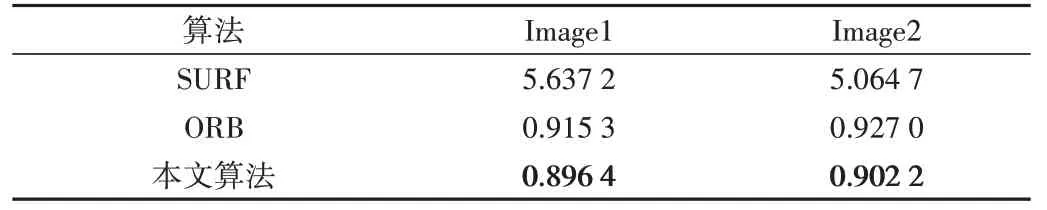
Table 3 Comparison of image mosaic speed表3 图像拼接速度比较 (s)
4.3 拼接图像质量比较
图像信息熵反映了图像信息的丰富程度,图像信息熵越大表示图像信息越丰富、质量越高[22]。采用图像信息熵指标对拼接图像质量进行评价,计算公式为:
式中,i为像素亮度值,pi为亮度值为i的像素数量与图像总像素个数之比。
由表4 可知,在两组影像实验中,ORB 算法的拼接图像信息熵最低,本文算法的拼接图像信息熵最高,可达6.807 9,说明其拼接图像质量高,对于后续图像的分析与使用价值更高。
图6 为本文算法分别对Image1 和Image2 的左右图像拼接融合后的结果图。可以看出,拼接后的图像没有重影、错位等问题,且通过拼接融合消除了图像的拼接痕迹,所得拼接图像真实自然、质量较高。

Table 4 Comparative analysis of mosaic image information entropy表4 拼接图像信息熵比较
5 结语
为提高无人机遥感影像拼接质量,本文提出一种基于改进ORB 的图像拼接算法。该算法首先采用多尺度FAST算法检测特征点,然后利用NNDR 算法和最优化几何约束获取高质量特征点,并计算变换矩阵,最后通过改进渐入渐出加权融合算法对图像进行拼接。所提算法性能相较传统图像拼接算法有所提升,在快速拼接图像的同时保证了图像质量。虽然所提算法能够实现图像快速准确拼接,但获取的特征点数量少于SURF 算法,不利于变换矩阵估计。在今后的研究工作中,将对如何获取更多数量的正确特征点进行深入研究,对变换矩阵进行更精确的估计,以实现高质量的图像拼接。
