Kernel-Shapelets：基于卷积网络的特征子序列学习方法

2023-05-11冯冠玺石小川

软件导刊 2023年4期

冯冠玺，马超，石小川，张典

（1.武汉大学国家网络安全学院；2.空天信息安全与可信计算教育部重点实验室，湖北武汉 430072）

0 引言

如今随着互联网、电子传感器等渗透到社会的各个领域，全球每天都会诞生海量的时序数据。股市中的股价走势、医学领域的心电图在一段时间内的变化，以及行走时手机传感器在x 轴、y 轴方向上的加速度变化都可看作时序数据，因此时序数据挖掘吸引了很多研究者关注。时序数据分类作为其基础任务，近年来一直是研究的重点。目前，研究者们已提出上百种时间序列分类方法［1］。这些方法可分为3 类：①基于全局距离的分类方法；②基于特征的分类方法；③基于深度学习的分类方法。

基于全局距离的分类方法较为简单。早期研究者直接将最近邻方法（One Nearest Neighbor，1NN）和欧氏距离（Euclidean Distance）方法应用到时序分类中，但无法处理因时间序列发生扭曲变形而无法匹配的问题，因此分类表现较差。为了解决这一问题，研究者尝试使用1NN 和动态时间规整（Dynamic Time Warping，DTW）距离方法［2］对时序数据进行分类。该方法虽在分类表现上优于欧氏距离，但时间耗费更多。后续有学者陆续提出各种基于DTW 的分类方法的变种［3-4］，但基于全局距离的分类方法始终无法避免同一个问题：仅考虑全局特征会导致时间序列的局部特征被噪声数据所淹没。

为了解决这一问题，文献［5］提出特征子序列（Shapelets）概念，至此基于特征的分类方法成为新的研究热点。特征子序列可看作是一类时间序列中最具有辨识性的子段，由于该方法聚焦于寻找局部特征，因此在全局相似但局部差异较大的数据集中具有更好的表现。此外，特征子序列方法因能给出原时间序列中的关键部位，所以具有较强的可解释性。在文献［5］的基础上，文献［6］筛选出最佳的k 条特征子序列，并基于这些特征子序列将时间序列转换为仅含有k 个属性的个体，在进一步扩大了分类器选择范围的同时，降低了时序数据维度。此后的特征子序列相关研究主要致力于提高搜寻筛选特征子序列的速度和准确度两个方向上。

随着深度学习技术在机器视觉、自然语言处理等领域得到广泛应用［7-9］，研究者们开始尝试将深度学习技术应用于时间序列分类领域。文献［10］将多层感知机（Multi Layer Perception，MLP）、全卷积神经网络（Fully Convolutional Networks，FCN）、残差网络（Residual Networks，ResNet）等网络模型应用到时序分类任务中，其中有些模型取得了与传统37 个分类器集成的COTE［11］方法相当的表现。然而，相较于具有较强可解释性的传统模型，深度学习模型被视为黑盒模型，研究者们很难从中找出模型的判断依据。

综上，基于特征子序列的方法虽具有较强的可解释性，但受限于传统机器学习的学习能力，无法生成准确的特征子序列以提高分类表现。得益于强大的学习、拟合能力，深度学习在时序分类的表现上优于其他方法，但端到端的黑盒模型并不具有解释性。

为了改善上述问题，本文首次提出将卷积神经网络（Convolutional Neural Network，CNN）中的卷积核（Kernel）作为特征子序列的概念，并据此改造CNN 网络，使CNN 网络能够定位原时间序列的关键子段，从而增强了CNN 模型的可解释性。

本文的主要贡献如下：

（1）首次提出将CNN 网络中的卷积核作为特征子序列的思想，拓宽了特征子序列的概念。

（2）改造CNN 网络结构，提出基于CNN 网络模型提取特征子序列的方法。

（3）结合特征子序列思想提出一种针对时序领域的可解释性算法。

（4）通过在 UCR 公开数据集上进行实验，本文将Kernel-Shapelets 方法与现有基于全局距离的方法、基于特征的方法和基于深度学习的方法在分类表现、可解释性等多个方面进行了比较。

1 概念与定义

1.1 时间序列

任何以时间先后顺序排列的实数序列都可视为时间序列：

给定一条长度为m 的时间序列T，T中长度为l的子段被称为时序子序列：

训练集中所有时间序列的子序列组成了特征子序列的候选集。

1.2 距离度量

两条时间序列之间的差异大小一般用“距离”概念来表示。在以往的研究中，研究者通常采用欧式距离作为距离度量公式。设两条时间序列T和T′长度为m，其欧式距离计算公式为：

1.3 特征子序列

文献［5］首次提出特征子序列（Shapelets）概念，并将特征子序列定义为时间序列中最能代表其类别特征的子序列。为了从数据集中筛选出最佳特征子序列，采用信息增益（Information Gain）作为特征子序列的评价标准，信息增益越大，越能代表该类时间序列。

1.4 基于特征子序列的数据表征

广义上的基于特征子序列的数据表征（Shapelets Transformation）指通过某种映射将时间序列转换到新的维度空间。例如，文献［6］、［12］将k 条特征子序列与时间序列之间的欧式距离作为时序数据的k 维特征，其转换过程如图1所示。

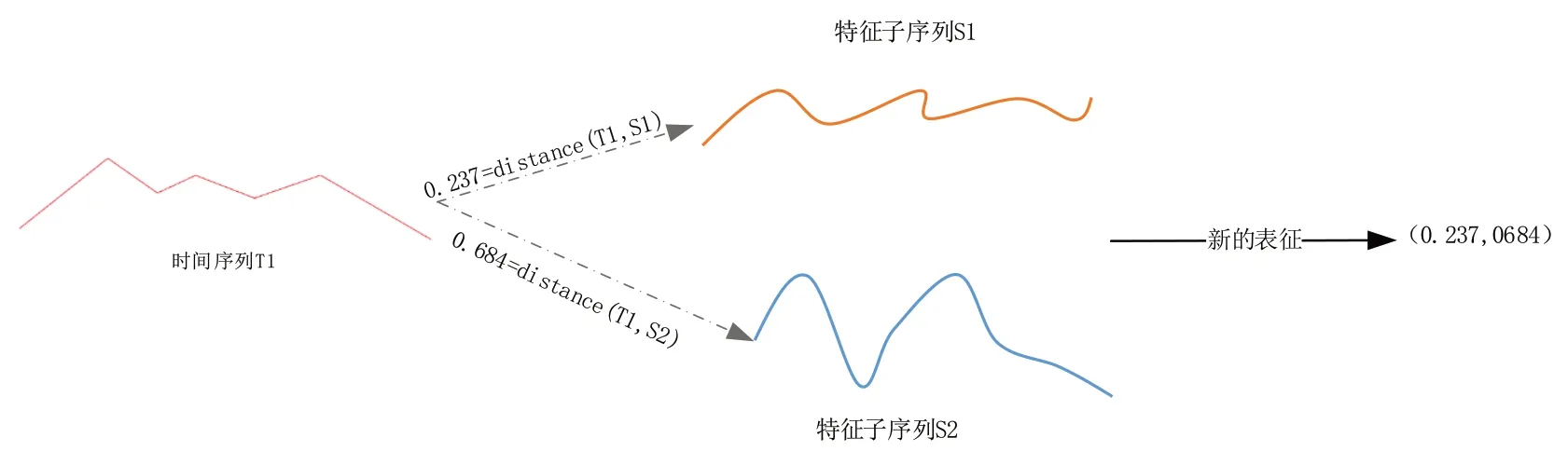
Fig.1 Distance-based shapelets transformation method图1 基于距离的特征子序列表征方法

2 相关工作

2.1 基于全局距离的分类方法

早期时序数据分类往往基于全局距离方法。研究者最早使用欧氏距离作为距离度量标准，该方法易于理解且计算简单，但点对点的距离计算方式在面对同种类别但相位不同的两条时间序列时，度量结果会存在很大误差。为了解决这一问题，研究者将动态规划引入到距离计算方法中，提出了DTW 算法［2］。通过动态规划，DTW 能够将时间序列拉伸或收缩，从而尽可能减小相位偏移造成的误差。但动态规划算法的引入也导致DTW 算法的时间复杂度增长为O(n2)，其中n为时间序列长度，而欧氏距离的时间复杂度仅为O(n)。由于时间序列维度可以达到几百甚至上千维，因此DTW 带来了巨大的时间耗费。后续学者提出一系列DTW 算法加速的研究，但基于全局距离的分类方法始终无法解决时序数据局部特征被高维度和噪声所淹没的问题。

如图2 所示，两类树叶整体形状相似，但在叶柄部位，一类树叶呈直角，另一类树叶呈钝角。通过顺时针扫描，并计算树叶轮廓与中心点之间的距离，可将树叶轮廓延展为时间序列并进行分类。然而，当两类树叶整体轮廓相同而仅有少量局部不同时，基于全局距离的方法无法正确地进行分类。

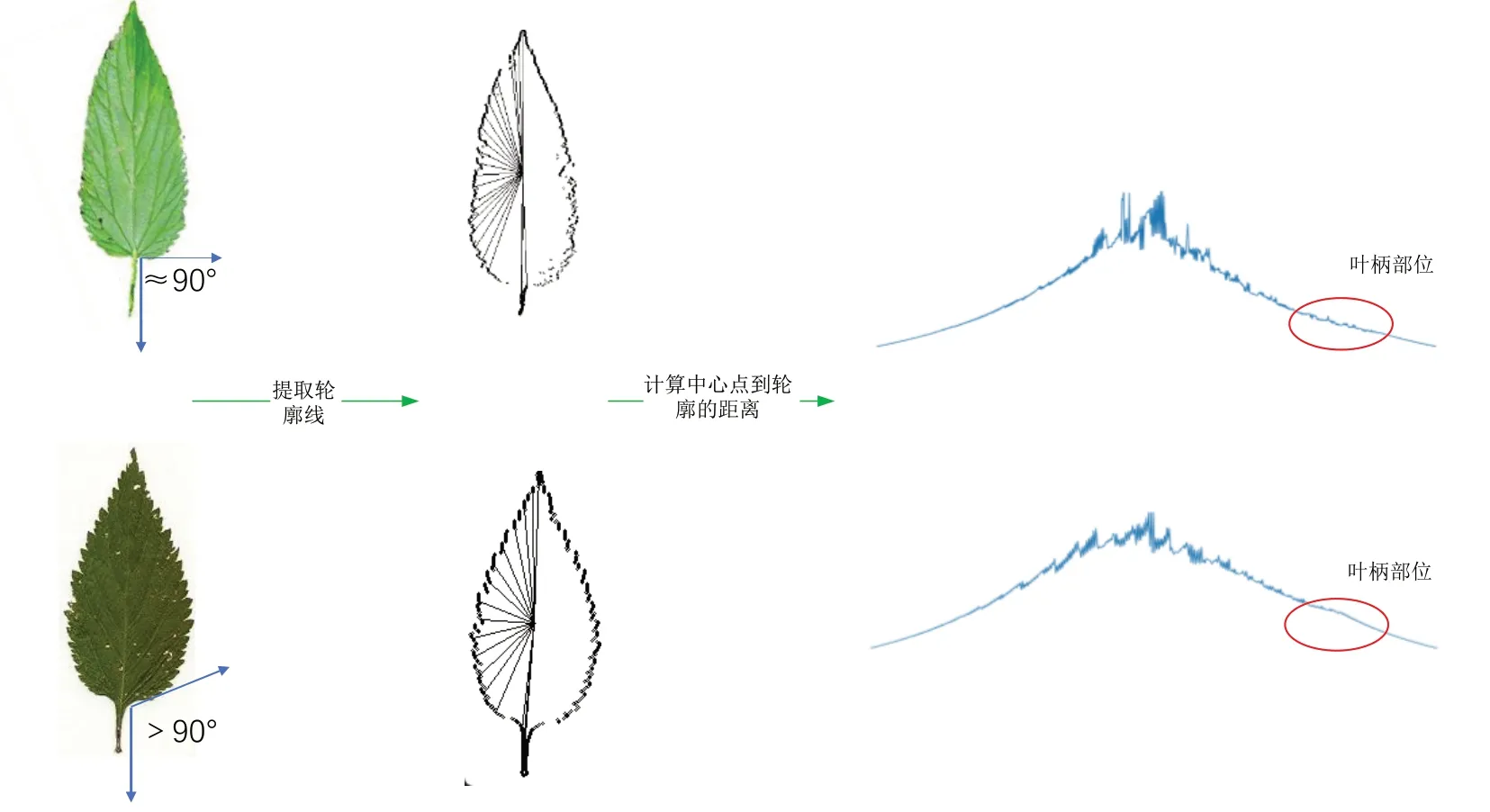
Fig.2 Overall outline of the two types of leave图2 两类树叶整体轮廓延展示意图

2.2 基于特征子序列的分类方法

为了能够提取出局部特征，2009 年Ye 等［5］首次提出特征子序列概念。与以往关注全局距离的分类方法不同，基于特征子序列的方法将关注点放在了局部特征。研究者将决策树分类器与特征子序列筛选相结合，以信息增益为标准，在找出最佳特征子序列的同时，对时序数据进行分类。但其仍遗留两个缺陷：一是分类器与特征子序列的提取过程紧耦合，无法使用除决策树外的其他分类器；二是通过遍历特征子序列候选集来搜索最佳特征子序列所花费的时间过长。为此，2014年Hills 等［6］将特征子序列与分类器解耦合，通过找出top-k 条特征子序列，计算时间序列与k 条特征子序列之间的距离，并将该k 个距离数值作为时间序列的k 维属性值，通过这种方式表征后的数据集可使用各种分类器。同年，Grabocka 等［13］提出“Learning Time Series Shapelets（LTS）”概念，即特征子序列不再是从数据集中抽取得到的，而是通过学习得到的。研究者首先随机初始化k 条特征子序列，分别计算k 条特征子序列与时间序列的距离作为逻辑回归的k 个属性值，并通过交叉熵损失函数调整k 条特征子序列对应的权重及形状。该方法将特征子序列选择范围从训练集扩大到整个实数空间，但由于其整体模型采用逻辑回归分类器，学习能力与分类表现并不理想。

2020 年，Dempster 等［14］提出随机卷积核表征法（Random Convolutional Kernel Transform，ROCKET）方法，该方法将卷积核看作特征子序列，通过生成海量（默认为5 000个）、随机大小、随机权重的卷积核，将时序数据重新表征，并对表征后的数据使用线性分类器进行分类。由于无需学习、更新卷积核权重，ROCKET 方法的训练速度远超其他特征子序列方法。2021 年，研究者又提出Mini-ROCKET 方法［15］进一步加快了训练速度，但海量的卷积核导致权重过于分散，无法分辨出原时间序列中对分类有重要影响的部位。

2.3 基于深度学习的分类方法

随着深度学习在机器视觉、自然语言处理领域的迅猛发展，有研究者开始将深度学习技术应用于时序数据挖掘中［16-17］。在时序数据分类领域，Cui 等［18］提出多尺度卷积神经网络MCNN，该方法首先将原始时间序列分别进行平滑、下采样处理，并将处理后的时间序列与原序列拼接在一起，投放到只有一层卷积层的网络模型中。虽然该方法能够将单维时间序列扩展到多维，但需要进行大量的预处理，且实验证明该方法的分类表现较差［10］。Fawaz 等［10］将MLP、ResNet、FCN、MCNN、t-LeNet［19］、MCDCNN［20］、Time-CNN［21］、TWIESN［22］等 9 种方法在公开数据集上进行了实验对比，结果表明，基于卷积网络框架的ResNet 与FCN 明显优于其他算法。相较于传统模型，深度学习模型虽然具有更好的分类表现，但这些模型往往是端到端的黑盒模型，失去了可解释性。深度学习可解释性相关研究大多集中在计算机视觉领域，或者仅将已有的可解释模型迁移到时序领域，很少有针对时序数据设计可解释性模型的研究。

本文提出的方法Kernel-Shapelets 综合了CNN 网络的学习能力和传统特征子序列的可解释性，相比传统机器学习模型，CNN 网络强大的学习能力能生成更加精确的特征子序列，此外Kernel-Shapelets 首次提出利用特征子序列增强CNN 网络模型的可解释性。

3 Kernel-Shapelets卷积网络模型

3.1 卷积核与特征子序列

本文认为特征子序列与卷积核之间具有很多相似性：①特征子序列在整条时间序列之上按照一定步长滑动并计算距离，而卷积核在输入数据上也是按照一定步长进行滑动；②计算出一系列距离之后，以往的研究采用最小距离作为特征值，这与最小池化层的作用相同。本文通过公式推导可以得出：基于距离的表征方式可被视为基于卷积表征方式的特殊形式。

在文献［5］、［6］、［12］、［13］中，研究者将时间序列与子序列之间的距离作为表征后的特征值，仍设时间序列为T，长度为m，特征子序列为S，长度为l，距离表征数学表达式如公式（5）所示：

基于以上推导，本文重新对特征子序列作出定义：任何一段实数序列，只要满足如下要求便可视作特征子序列：①给定一条时间序列，该实数序列段能给出某种度量标准下的差异大小；②能通过该实数序列找出给定时间序列中的关键部分。

文献［14］、［15］虽然同样采用卷积核作为特征子序列，但其卷积核是随机生成的，且在整个训练过程中并没有通过学习更新卷积核内部权重，也无法通过卷积核定位原时间序列的关键部位。本文将利用CNN 网络学习生成更精确的特征子序列，并基于学习生成的特征子序列给出原时间序列的关键部位。

3.2 全局平均池化与全局最大池化

3.1节以数学形式证明了使用全局最大池化操作与传统Shapelets 方法采用最小距离作为特征在本质上保持一致。此外，相比于全局平均池化（Global Average Pooling Layer，GAP），全局最大池化操作能够保留更多位置信息。不同的池化操作对比如图3所示。

全局平均池化得出的特征值为平均特征，即该特征值为输入中每个位置数值的加权平均，该方式使得池化输出丢失了精确的位置信息。而全局最大池化的输出Outputpooling可通过argmax(Outputpooling)的方式迅速反向定位池化输出所对应输入中的位置，即全局最大池化的输出保留了位置信息，从而能够定位原时间序列中的关键位置。

由于全局最大池化操作与传统Shapelets 方法采用最小距离作为特征值的做法在本质上保持一致，且全局最大池化输出充分保留了位置信息，因此本文后续取消了全局平均池化层，而改用全局最大池化层。

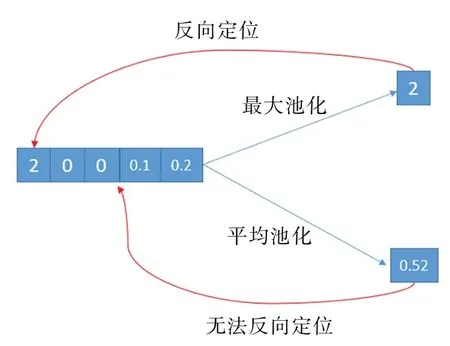
Fig.3 Comparison of different pooling operations图3 不同池化操作对比

3.3 网络模型结构

本文基于CNN 网络模型进行特征子序列的生成。与文献［10］中的CNN 网络框架不同，为了能够定位出原时间序列的关键部位，本文取消了全局平均池化层，改用全局最大池化层。整体模型如图4所示。

Fig.4 Overall network framework structure图4 整体网络框架结构

前三层的卷积层对原始时间序列进行去噪和特征提取。在3 层卷积操作后，通过全局最大池化层提取第三层卷积核各个通道与原时间序列之间的“距离”，之后通过线性全连接层进行分类。

3.4 特征子序列生成与原时间序列关键位置定位

卷积核越重要，越有可能成为特征子序列。在网络模型压缩过程中，一种较为简洁的思路是：基于全连接层的权重绝对值大小对卷积核进行剪枝，绝对值越小越容易被丢弃。本文延用这种思想，将权重绝对值大小作为卷积核重要性的数值标准，以此筛选出top-k 个卷积核作为特征子序列。

在找出top-k 个卷积核作为特征子序列后，基于算法1找出关键部位：

算法1基于重要卷积核定位原时间序列的关键部分

算法1 详细描述了基于重要卷积核定位原时间序列关键部分的过程。该过程主要分为两部分，第一部分是将原时间序列输入到训练好的模型中，通过前向传播获取最后一层卷积层中对应卷积核的输出。通过对输出进行遍历，找到输出中最大值所在位置。通过填充，卷积操作前后的维度与原输入维度保持不变，因此卷积核输出的最大值所在位置即为原时间序列中关键部分的起始时间点。图5 展示了基于Kernel-Shapelets 方法定位出GunPoint 数据集的关键位置（彩图扫OSID 码可见）。

Fig.5 Locate key positions of GunPoint dataset based on Kernel-Shapelet method图5 基于Kernel-Shapelet方法定位出GunPoint数据集关键位置

4 实验结果与分析

4.1 实验设置

为了验证Kernel-Shapelets 模型所生成特征子序列的有效性，本文利用Kernel-Shapelets 方法生成的特征子序列对数据集进行重新表征，并使用随机森林（Random Forest）作为分类器与其余基于特征子序列的方法以及深度学习模型在分类表现上进行比较。

本文的实验环境基于Win10 系统，显卡是NVIDIA Ge-Force RTX 2080Ti，代码基于Python 3.9 实现，Pytorch 库的版本为1.10.0。综合参考文献［10］中的实验设置，同时为了能够更公平地与其他模型进行横向对比，本文设置epochs 为2 000，学习率为0.001，每个数据集进行5 次实验，取分类表现最接近平均准确率的模型作为最终的实验模型。在基于特征子序列表征的过程中，筛选出100 条特征子序列，并将任一条时间序列转换为100维的特征向量。

4.2 数据集

UCR 时间序列仓库集（http：//www.cs.ucr.edu/～eamonn/time_series_data/）中目前一共有128 个数据集，但多数数据集规模较小，训练集中的时间序列条数在500 及以下的数据集有104 个。为了避免深度学习方法出现过拟合，本文选取仓库中所有训练集规模在1 500 条时序数据以上的数据集。数据集规模信息参见表1。

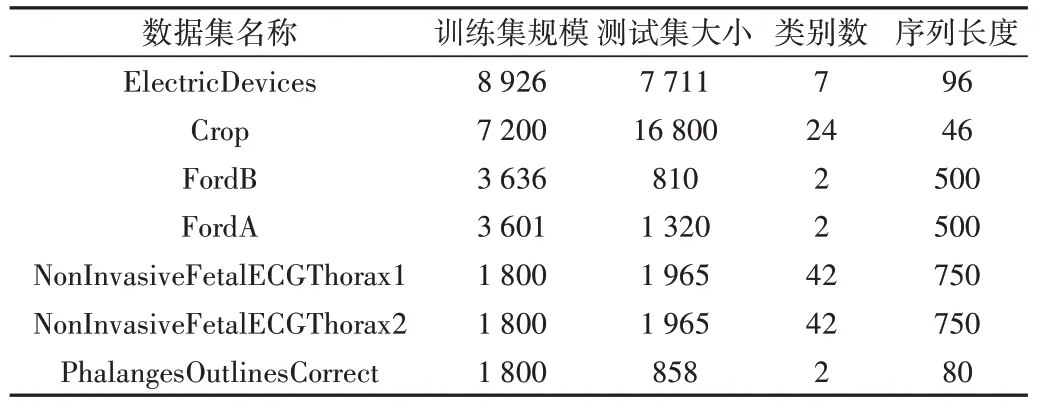
Table 1 Dataset size information表1 数据集规模信息

4.3 对比实验

目前，针对时间序列的分类方法基本可分为基于全局距离的方法、基于特征的方法以及基于深度学习的方法，本文也采用这3 类方法进行实验对比。在基于全局距离的方法中，选用分类表现较好的1NN+DTW 方法；在基于特征的方法中，选用Learning Shapelets 方法以及Fast Shapelets 方法，其中Learning Shapelets 属于学习生成式方法，而Fast Shapelets 为抽取式方法；在基于深度学习的方法中，选用FCN 方法与MCDCNN 方法。

4.4 实验结果分析

各模型分类准确率的实验结果如表2 所示。从表中可以看出，Kernel-Shapelets 的分类表现与FCN 十分接近，且优于其他分类器。

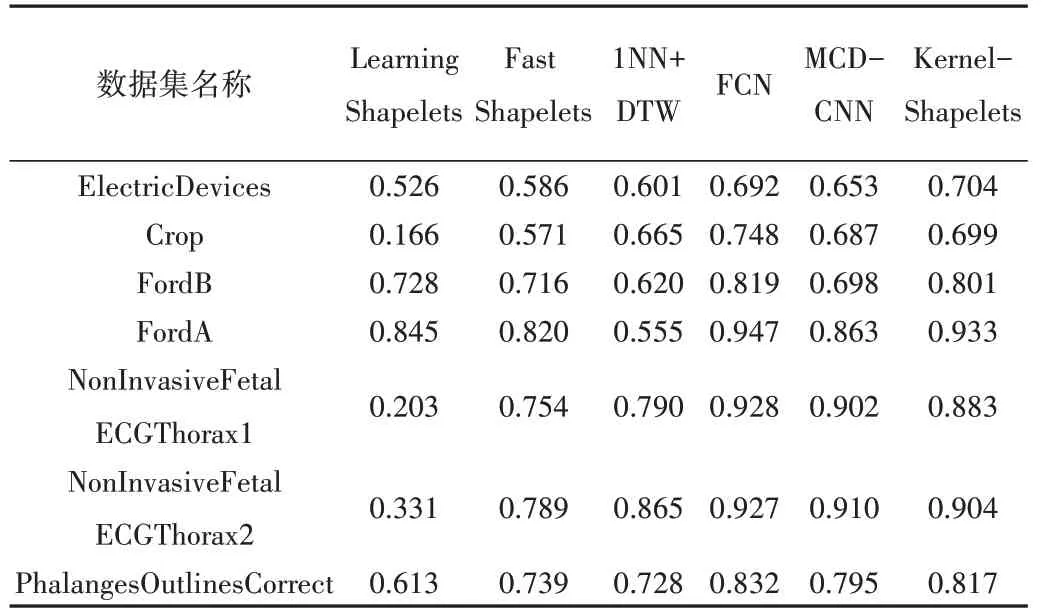
Table 2 Performance of each classifier表2 各模型分类准确率

从图6 的临界差分图（critical difference diagram）中也可以看出，本文提出的Kernel-Shapelets 优于其他Shapelets方法，仅次于FCN 模型，但本文方法提供了更强的可解释性，且对于长序列时序数据，经过特征子序列重新表征后的数据集规模更小。

Fig.6 critical difference diagram on classifiers图6 各分类器之间临界差分图

以FordB 为例，通过选取100 条特征子序列对数据集进行表征，表征后的数据集规模由3 636*500 变为3 636*100，而准确率仅由0.819 下降为0.801。表3 展示了表征前后的数据集规模大小变化与准确率下降情况。

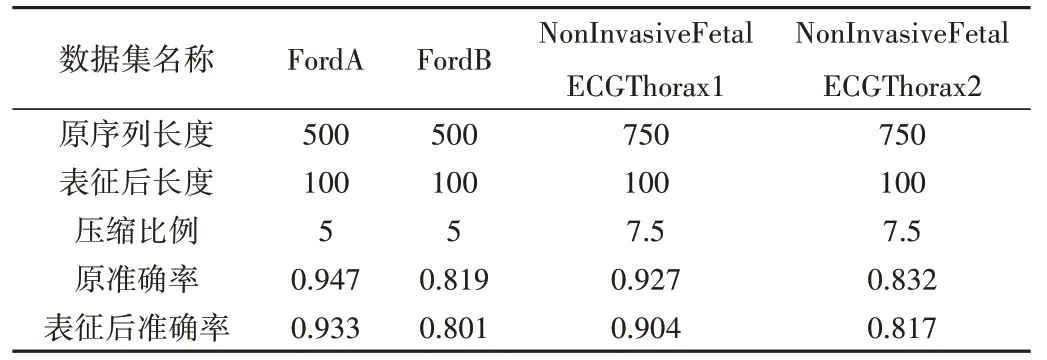
Table 3 Comparison of size and accuracy before and after representation of long series datasets表3 长序列数据集表征前后规模及准确率对比

在可解释性表现方面，以GunPoint 数据集为例对Kernel-Shapelets 的可解释性进行说明。本文分别通过Kernel-Shapelets 方法和Learning Shapelets 方法生成两条特征子序列，并基于这两条特征子序列将数据集中的每条时间序列转换为具有二维特征的个体。图7 展示了经过表征后，GunPoint数据集不同类别个体的分布情况。

从图7（a）中可以清楚地看出，经过Kernel-Shapelets表征后，不同类别个体之间的界限更加清晰，研究者可更加清晰地指出不同类别之间的差异。而在图7（b）中，基于Leaning Shapelets 表征后的数据集个体界限仍然不够分明，这也从一定程度上解释了Kernel-Shapelets 的分类表现优于Leaning Shapelets 的现象。

5 总结与展望

在时序数据分类领域，深度学习模型相较于其余分类模型具有更好的分类表现，但缺少了可解释性。综合借鉴深度学习的学习能力和特征子序列的可解释性，本文提出一种基于卷积网络生成特征子序列的方法Kernel-Shapelets，该方法基于全连接层权重筛选出top-k 个卷积核作为特征子序列，并将这些卷积核对应的全局最大池化层的输出作为特征值。通过采用UCR 时序仓库中训练集规模在1 500 以上的数据集进行实验，证明了Kernel-Shapelets 的分类表现优于其他特征子序列模型，能够在保证分类表现不下降或轻微下降的情况下提高模型的可解释性。