可变形天然裂缝动态宽度流固耦合计算模型

2023-05-10高佳佳陈一凡

西南石油大学学报(自然科学版) 2023年2期

彭浩，李黔，高佳佳，尹虎，陈一凡

1.中国石油集团川庆钻探工程有限公司川西钻探公司，四川成都610051 2.西南石油大学石油与天然气工程学院，四川成都610500

引言

天然裂缝动态宽度是指裂缝性地层发生漏失时，缝内流动净压力与天然裂缝壁面形变流-固耦合至稳定状态后沿着漏失侵入距离不同时刻的井下裂缝宽度分布，它既可为漏失体积和漏失速率的模拟预测提供初始条件，也可为堵漏材料的颗粒级配提供科学依据[1-4]。裂缝堵漏实验现已取得了很好的堵漏效果[5-8]，但在现场堵漏应用时远不及实验室的堵漏成功率[9]，原因为天然裂缝动态宽度未知，不能设计具有针对性的堵漏配方。目前，通过成像测井、声波测井和核磁共振只能识别天然裂缝的缝口宽度[10-11]，且在井漏时不宜进行测井作业。部分学者基于平板型天然裂缝的漏失动力学模型建立了天然裂缝平均宽度的预测模型：Sanfillippo 等[12]运用牛顿流体建立了平均宽度的计算模型；因牛顿流体描述钻井液流变性的局限性，Lietard 等[13]运用宾汉流体，通过无因次变化法，建立了理论漏失特征曲线图版，运用图版法结合井漏录井数据反演出了平均宽度；Verga 等[14]对此方法的可靠性进行了验证；为便于现场使用，彭浩等[15]通过自适应搜索法简化了求解过程，提高了模型求解精度与速度。但是，大多数井下天然裂缝在缝内净压力作用下会发生变形：可变形天然裂缝在缝内流动净压力压缩下呈线性变形规律[16-18]；在几兆帕缝内净压力下，对于变形较大的可变形天然裂缝其宽度增量可达几毫米[1，4，19-21]，故平板型漏失动力学建立的天然裂缝平均宽度预测模型不再适用。

为解决可变形天然裂缝的动态宽度计算问题，本文运用宾汉流体模型，结合天然裂缝的变形控制方程和钻井液漏失的物理特征，建立可变形天然裂缝动态宽度流-固耦合计算模型，模型将不需要测量地层的岩石力学参数及地应力，仅需现场测量的钻井液性能、漏失速率及漏失体积序列数据，就能反演出可变形天然裂缝的动态宽度。

1 裂缝性地层流-固耦合漏失动力学模型

对于可变形天然裂缝，钻井液因井底压差在裂缝中漏失产生壁面挤压力pN挤压裂缝壁面使之发生变形，同时，裂缝壁面因变形也会对缝内钻井液产生反作用压力ps，进而影响缝内流动净压力的分布，最终流-固耦合至稳定的缝内流动净压力p（r）（图1）。

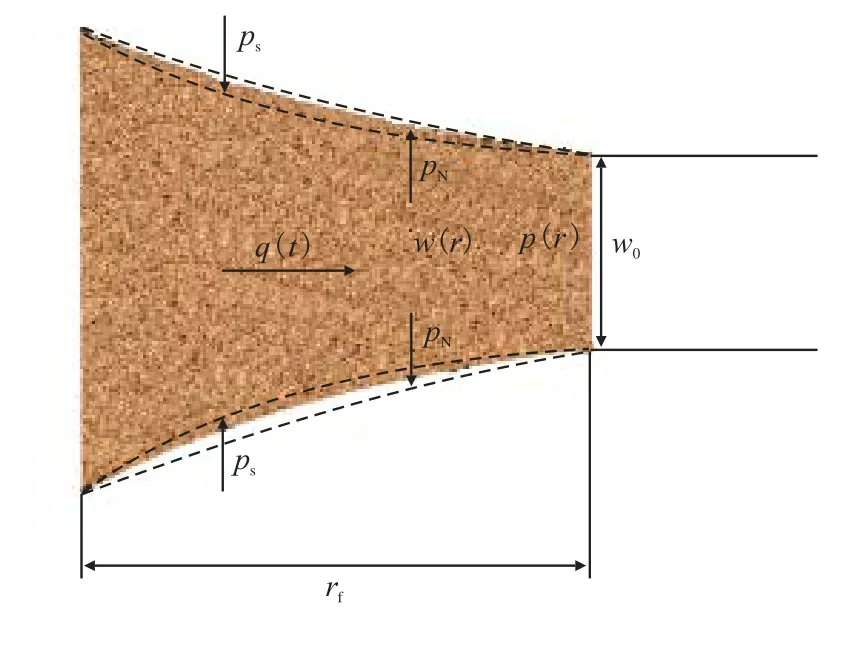
图1 裂缝性地层漏失流-固耦合示意图Fig.1 Hydro-mechanical coupling of leakage in fractured formations

1.1 漏失动力学模型建立及求解

基于宾汉流体模型，可建立钻井液在天然裂缝中漏失的压降微分方程[13]

钻井液流入天然裂缝内产生缝内流动净压力，作用于裂缝壁面，使其发生变形，根据线性变形规律，可得天然裂缝动态宽度为[16-18]

裂缝内沿着径向的流动净压力分布为[22]

分析式（3）可知，在缝口处r=rw，p(r)=∆p，为井底压差；在漏失前端处r=rf，p(r)=0，为原缝内压力。

将式（3）代入式（2）可知，天然裂缝动态宽度分布为

若以单位时间∆t进行推演，则每当时间增加∆t，漏失前端距离将由rf(n−1)增加至rfn（n≥2），漏失体积将增加∆VFn，如图2 阴影部分所示，∆VFn由漏失前端距离增加和天然裂缝形态改变两部分的体积增量之和构成，总的漏失体积可由单位时间∆t的漏失体积累加得到，即VF=∑∆VFn；同时，根据图2所示的几何关系可得到漏失体积的控制方程

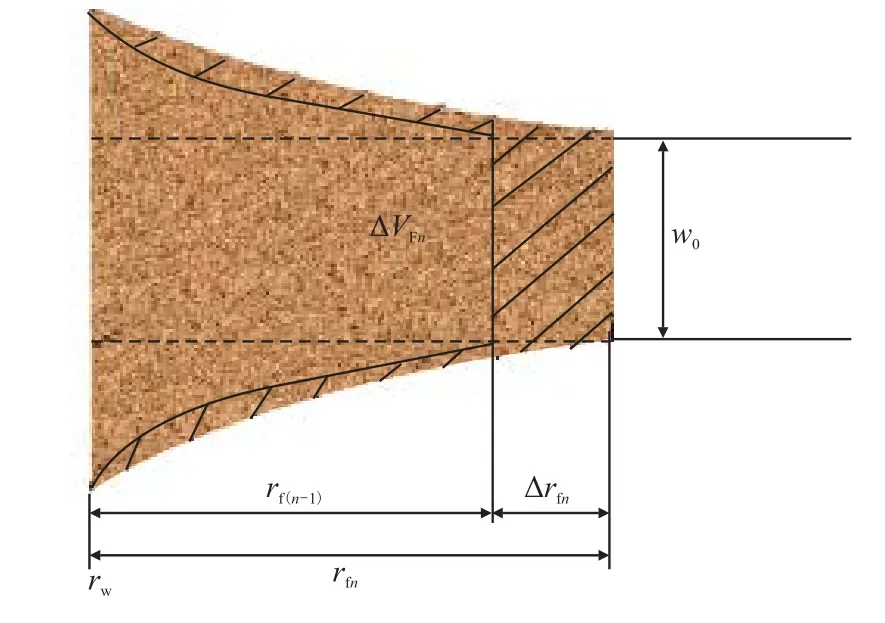
图2 天然裂缝变形漏失体积增量示意图Fig.2 Diagram of natural fracture deformation loss volume increment

在得知漏失体积的表达式后，可根据漏失速率和漏失前端侵入速度的物理意义，得到其表达式为

将式（4）和式（5）代入式（6），可得漏失速率的几何控制方程

其中，Q的表达式为

将式（4）、式（6）及式（7）代入式（1），并对压力做rw→rf积分，可得漏失前端侵入速度的控制方程

对于F1(r) 和F2(r) 分析可知，难以获得解析解，只能进行数值积分。对式（9）变形分析可得到任意时间（漏失前端距离为rf）不同位置r∈(rw,rf)处的缝内压降，用井底压差与之相减便可得到缝内任意时间不同位置的缝内流动净压力分布

由式（12）求得的缝内流动净压力记为pI(r)；由式（3）求得缝内净压力记为pII(r)；通过判定它们是否满足求解精度以确定C是否合理，整个求解过程分为初值确定和递推预测两大步，具体求解步骤如下

1）输入基本参数：∆p、τy、µp、w0及KFrac。

7）将计算所得的rf(tn)、C(tn) 代入式（7）、式（6）、式（12）及式（4），计算漏失速率q(tn)、漏失体积VF(tn)、tn时刻的缝内流动净压力p(tn)及天然裂缝宽度w(tn)。

其中，步骤2∼步骤4 为初值确定，步骤5∼步骤7 为递推预测。

1.2 漏失动力学模型求解方法验证及漏失模拟

法向刚度系数KFrac=50 000 GPa/m，由式（2）可知，当井底压差∆p=5 MPa 时，其裂缝宽度增量最大为0.1µm，天然裂缝几乎不变形。为验证本文模型，在该条件下运用本文模型，与Lietard 所提出的无因次求解方法进行计算对比[13]，同时，为分析天然裂缝变形对漏失特征的影响，取KFrac=30 GPa/m 进行漏失模拟，结果如表1 所示。

表1 基础参数值Tab.1 Basic parameter values

根据两种方法得到的关于漏失前端距离（图3）、漏失速率（图4）及漏失体积（图5）的计算结果对比图可知，本文的求解方法与Lietard 所提出的无因次求解方法计算结果一致。

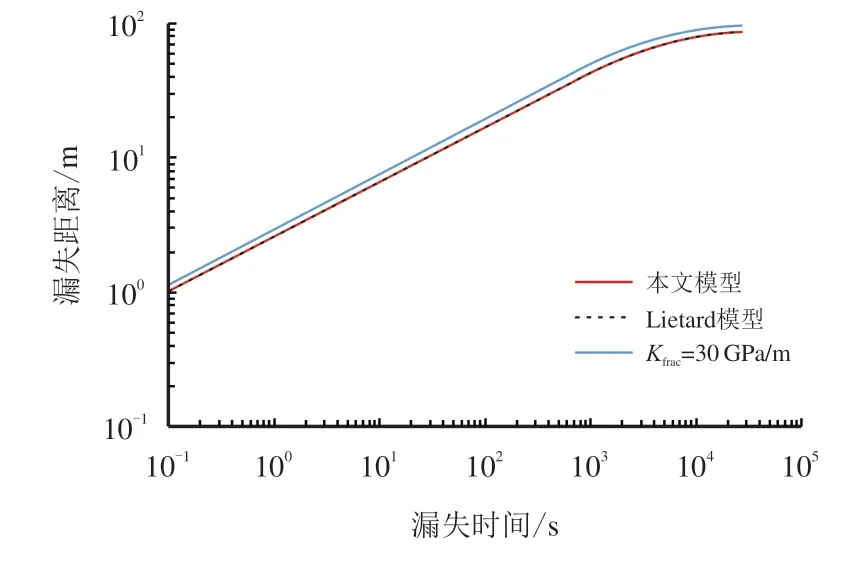
图3 漏失前端距离计算结果对比示意图Fig.3 Diagram of comparison of calculation results of leakage front distance

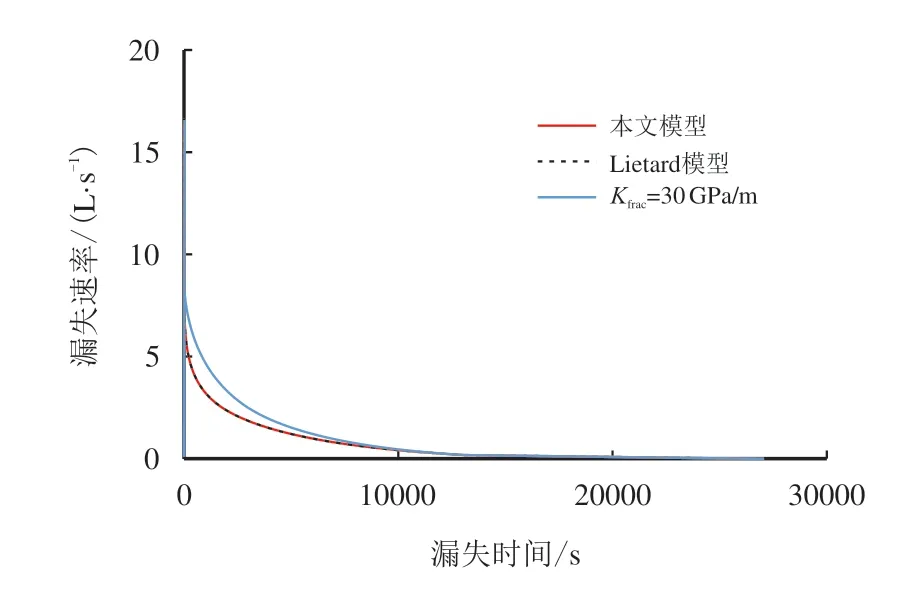
图4 漏失速率计算结果对比示意图Fig.4 Diagram of comparison of calculation results of leakage rate

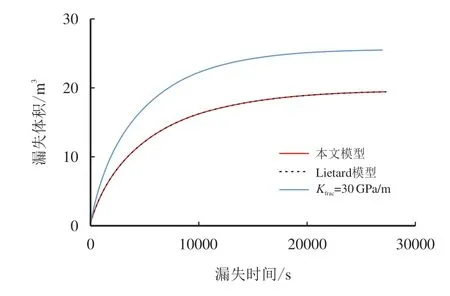
图5 漏失体积计算结果对比示意图Fig.5 Diagram of comparison of calculation results of leakage volume

由图3∼图5 的模拟结果可以看出，本文模型与Lietard 所提出模型的计算结果一致，验证了模型的可靠性。由图3∼图7 可知，天然裂缝变形对漏失特征的影响为：可变形天然裂缝，相较于平板型天然裂缝，其在发生漏失时横切面积更大，导致流动压耗更小，进而在相同的漏失时间内漏失半径、漏失速率及漏失体积更大；随着漏失前端距离增加，天然裂缝宽度呈动态变化，缝口宽度最大，漏失前端为天然裂缝的初始宽度，最终天然裂缝将呈梯形形态分布（此时钻井液因动切力而停止流动，缝内压力呈线性降低）；同一漏失深度的缝宽随着漏失前端距离增加而变宽，且在天然裂缝呈梯形形态分布时达到最大，此时天然裂缝形态系数为1。

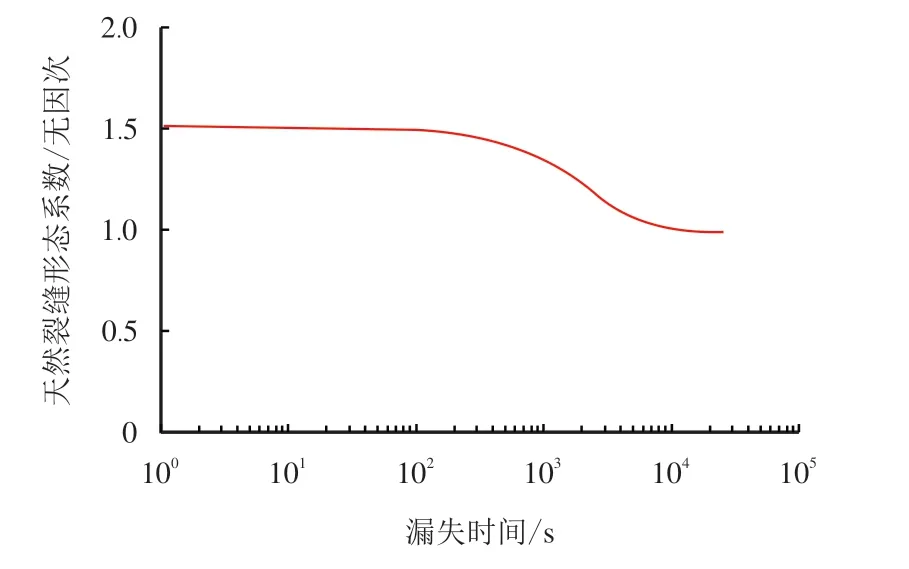
图6 KFrac 为30 GPa/m 的天然裂缝形态系数随时间分布图Fig.6 Distribution of the natural fracture shape coefficient with KFrac=30 GPa/m

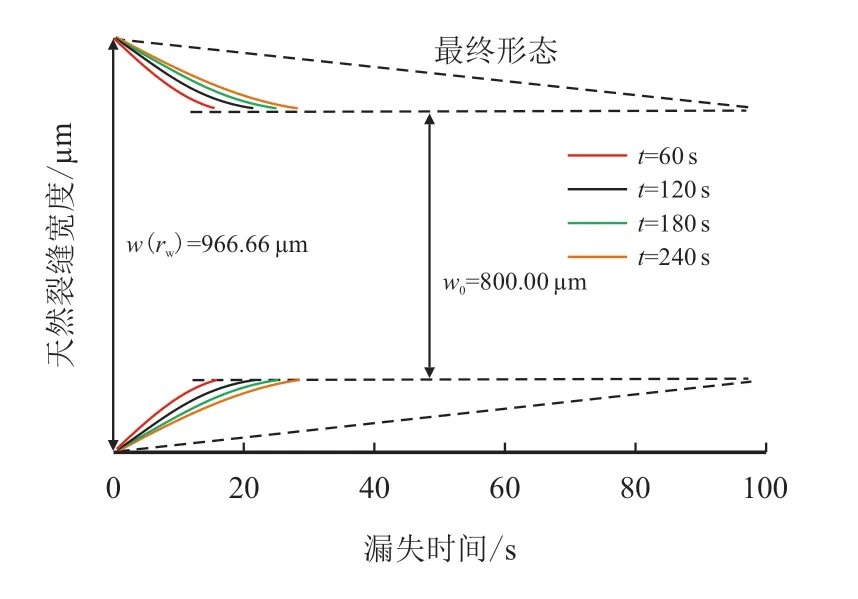
图7 KFrac 为30 GPa/m 的天然裂缝动态宽度示意图Fig.7 Diagram of the dynamic width of natural fracture with KFrac=30 GPa/m

2 天然裂缝动态宽度流-固耦合计算模型建立

根据式（2）天然裂缝动态宽度的定义可知，当裂缝壁面变形小时，其值等于天然裂缝平均宽度（也为天然裂缝的初始宽度）；当裂缝壁面变形较大时，其值为缝内流动净压力与裂缝壁面变形流-固耦合至稳定状态的裂缝形态。

2.1 平板型天然裂缝动态宽度模型

当钻井液在裂缝壁面变形小的天然裂缝中漏失时，其动态宽度等于天然裂缝平均宽度，可将其视为平板型模型（图8）。

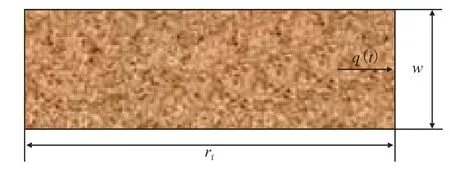
图8 平板型天然裂缝漏失示意图Fig.8 Diagram of the flat natural fracture leakage

根据几何关系可知漏失体积VF(t)的表达式为

Lietard 等[13]通过对式（13）和式（1）变形积分和无因次变化得到

为解决图版求解速度慢及图版盲区匹配易产生人为误差的问题，笔者提出了自适应搜索法求解[15]，通过研究可知，对任意一条理论漏失曲线均有一段线性相关系数达到0.999 的近似直线段（图9），实钻漏失曲线与其具有相同形态，故也存在近似直线段；通过自适应搜索法自动设置α 步长，求取不同α 对应理论漏失特征曲线直线段的斜率，然后，取实钻漏失曲线直线段数据，运用最小二乘法计算其斜率，比对两者斜率直至其相对误差在设定范围内；最后，确定对应斜率的理论漏失特征曲线，取其无因次有限侵入值α，反演出平板型天然裂缝漏失的平均宽度，具体计算步骤参考文献[15]。

2.2 可变形天然裂缝动态宽度模型

当可变形天然裂缝发生漏失时，其动态宽度为壁面岩石与缝内流动净压力流-固耦合至稳定状态的裂缝几何形态（图1）。分析实钻漏失曲线横纵坐标的表达式式（17）、式（18）可知，由于横纵坐标项里分别有lg w、−2 lg w，天然裂缝宽度w 不再是定值而是rf、t的函数[式（4）]，将导致实钻漏失曲线的近似直线段变成曲线（图10），此时不能通过简单的曲线匹配反演裂缝动态宽度。基于分段原理，在∆t时间内，取漏失时间ts、ts+∆t以及对应的漏失体积V(ts)和V(ts+∆t)，代入式（17）、式（18）可绘制ts、ts+∆t的实钻漏失曲线点：（记为点P1），（记为点P2）。如图10 所示，点P1 和点P2 可确定一条直线并求得其斜率，由自适应搜索法可知，当求得直线斜率便可求得其对应的天然裂缝平均宽度，并将所求得的天然裂缝平均宽度定义为天然裂缝等效平均宽度，记为wave。

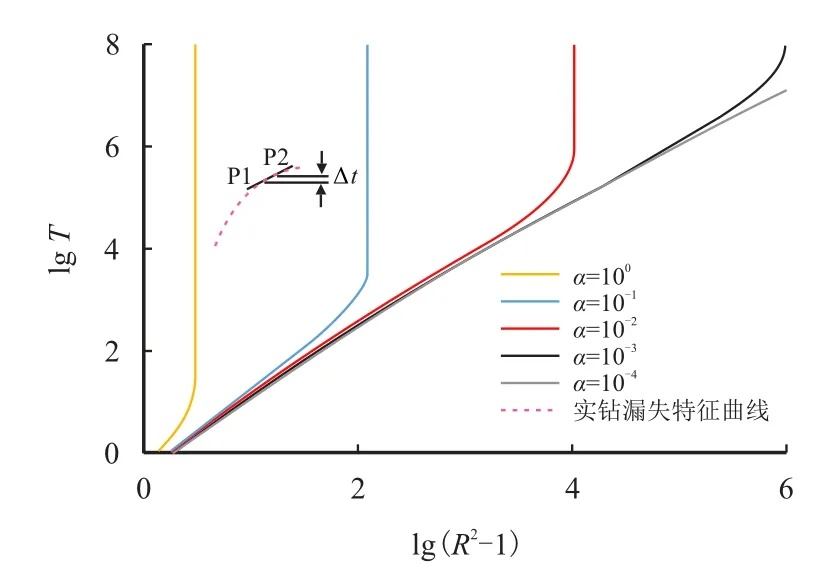
图10 运用自适应搜索法求wave 原理图Fig.10 The principle of using adaptive search method to find wave

如图11 所示，漏失前端距离每增加∆rfn将增加漏失体积∆Vaven，因天然裂缝动态宽度是连续变化且不存在突变所以满足体积等效原则，进而∆VFn=∆Vaven。根据累加原则，漏失前端为rfn的总漏失体积分别为，∑∆VFn、∑∆Vaven，因为∆VFn=∆Vaven，所以∑∆VFn=∑∆Vaven，即为VFn=Vaven。最终，根据几何关系可知天然裂缝等效平均宽度wave和天然裂缝宽度w(r)有着以下关系（图1，图11）

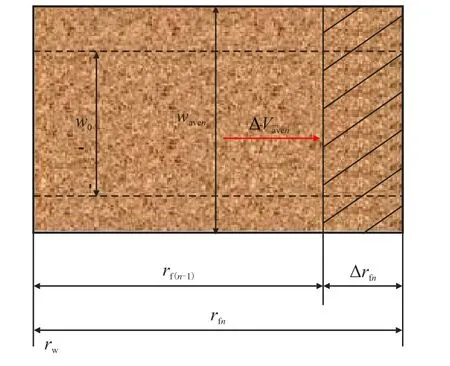
图11 天然裂缝等效平均宽度漏失增量示意图Fig.11 Diagram of loss increment of equivalent average width of natural fractures

裂缝性漏失发生后可读取漏失速率序列q(t1)，q(t2)，q(t3) …以及漏失体积序列VF(t1)，VF(t2)，VF(t3)…，结合钻井液流变性参数，运用自适应搜索法可求得天然裂缝等效平均宽度序列wave1，wave2，wave3…，将其代入式（19）求得不同时间的漏失前端序列rf1，rf2，rf3…及∆rfn。同时，将式（4）代入式（19）化简可得到天然裂缝初始宽度w0与天然裂缝等效平均宽度waven的关系为

由式（20）分析可知，在求得天然裂缝等效宽度waven、钻井液漏失前端rfn的条件下，若知道天然裂缝法向刚度系数KFrac及天然裂缝形态系数Cn[Cn=C(tn)]，便可得到天然裂缝的初始宽度w0。其中，KFrac为定值由天然裂缝壁面岩石类型以及围压环境决定其值，C为时间的函数，为求得w0可先给KFrac假设一个初值代入式（20），则w0仅为Cn的表达式（rfn是时间t的函数，w0为定值）。最后，将所求得的rfn序列、w0表达式代入式（7）可得漏失速率q(t)的表达式

其中

分析可知，在q(t)、KFrac、waven及rfn已知的情况下，式（21）为天然裂缝形态系数C的隐式表达式，可通过二分法进行求解得到C1，C2，C3…序列。其中，KFrac为假设值，结合所求得的Cn、rfn，代入式（20），可求得假设的KFrac值下天然裂缝初始宽度w0，将Cn，rfn，KFrac，w0代入式（9），可求得该假设KFrac值下的，根据天然裂缝形态的约束条件式（24）判定KFrac的合理性（同一漏失前端距离rfn在同一漏失速率q(t)|r=rfn为KFrac的多解函数，但每一KFrac值对应唯一的漏失前端侵入速度），若不满足约束条件，则修正KFrac的值直至满足约束条件式（24），得到合理的KFrac。最后，根据该KFrac值，可及时计算测量时间段的C、w0及w(r,t)。

对于非测量时间段（预测）的漏失速率q(r)、漏失体积VF(t)、不同时刻的天然裂缝动态宽度w(r)可根据1.1 节的求解方法进行预测，只是其初始条件改变为C(ts)、rf(ts)。

综上所述，天然裂缝动态宽度的求解过程分为测量时间段和预测时间段（图12），具体步骤如下。

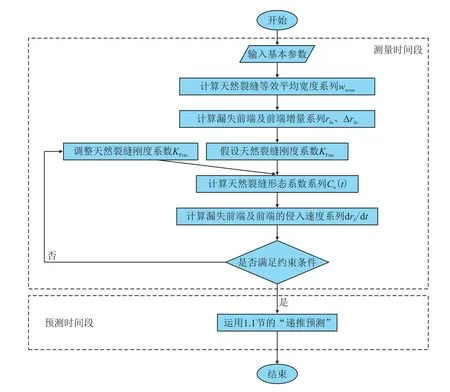
图12 天然裂缝动态宽度计算流程图Fig.12 Flow chart for calculating the dynamic width of natural fracture

1）读取漏失速率序列q(t1)，q(t2)，q(t3)…及漏失体积序列VF(t1)，VF(t2)，VF(t3)…，输入钻井液流变性τy、µp。

2）运用自适应搜索法可求得天然裂缝等效平均宽度序列wave1，wave2，wave3…，代入式（19）求得rf1、rf2、rf3…及∆rfn。

3）假设裂缝法向刚度系数KFrac，将求得的wave1，wave2，wave3…及rf1，rf2，rf3…代入式（21）运用二分法求得C1，C2，C3…。

4）求取假设KFrac条件下的w0、drfn/dt，判断是否满足约束条件式（24），若不满足修正KFrac，重复步骤3 直至满足式（24）。

5）运用求得的合理KFrac，计算测量时间段的C、天然裂缝初始宽度w0及天然裂缝动态宽度w(r)。

6）对于非测量时间段（预测）的漏失速率、累加漏失量及天然裂缝动态宽度运用1.1 章节的“递推预测”方法进行计算，其初始条件为：C(ts)、rf(ts)。

3 实例计算

川西XX 井垂深2 906 m 时，发生井漏，由地质资料及邻井资料可知，该处天然裂缝发育，其测量的漏失速率及漏失体积见图13。此时，井眼尺寸为ϕ311.2 mm，井底压差∆p为4.8 MPa，钻井液动切力τy为15 Pa，塑性黏度µp为38 mPa·s。

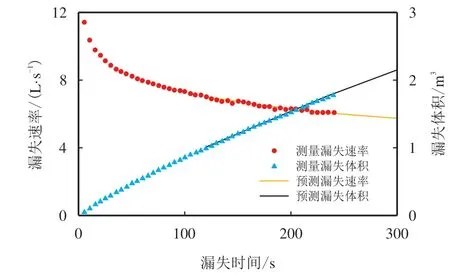
图13 测量和预测漏失速率及漏失体积Fig.13 Measured and predicting leakage rate and leakage volume

图13 为测量和预测的漏失速率和漏失体积数据，根据2.2 章节步骤1 先读取漏失速率及漏失体积数据，其中，预测漏失速率、漏失体积是在求得天然裂缝初始宽度和法向刚度系数后，以时间120 s 为初始条件计算所得到的；根据2.2 章节步骤2 自适应搜索法可求得天然裂缝等效平均宽度waven，进而求得rfn及∆rfn序列（图14）；运用2.2章节步骤3 及2.2 章节步骤4 可求得裂缝法向刚度系数KFrac=29.7 GPa/m，天然裂缝初始宽度w0为758.01 µm；根据2.2 章节步骤5 可求得测量时间段的天然裂缝形态系数（图15）和天然裂缝动态宽度（图16）。

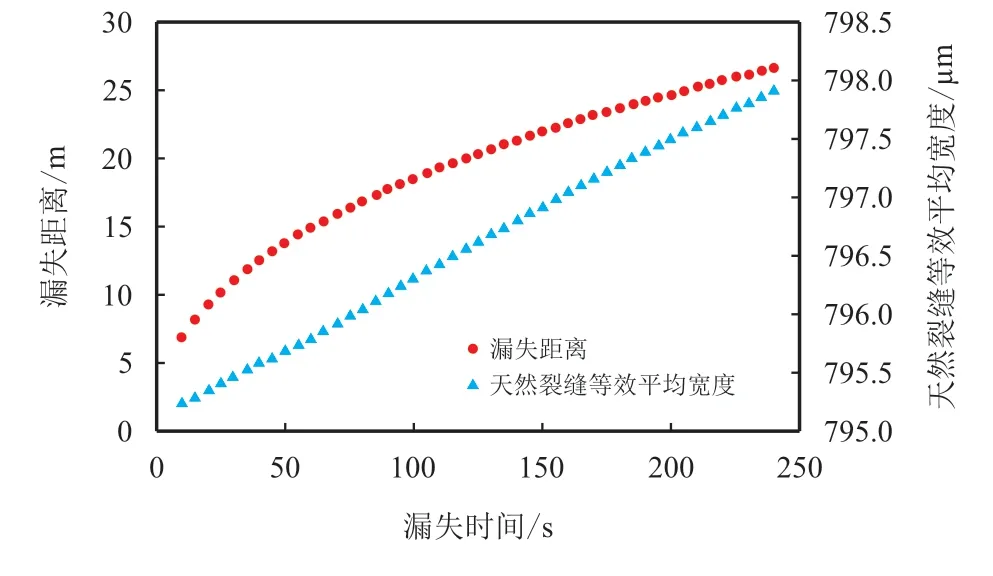
图14 不同时刻漏失前端距离及天然裂缝等效平均宽度图Fig.14 Diagram of the leakage front distance and the equivalent average width of natural fracture

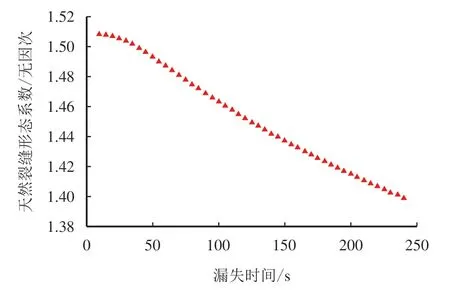
图15 天然裂缝形态系数C 随时间的分布图Fig.15 Distribution of the natural fracture shape coefficient C over time

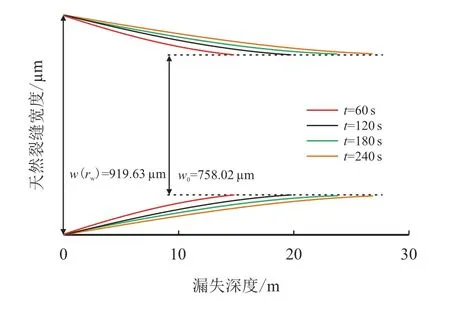
图16 不同时刻天然裂缝的动态宽度图Fig.16 Dynamic of the dynamic width of natural fracture at different moments

根据计算结果可知，裂缝法向刚度系数KFrac为29.7 GPa/m，天然裂缝初始宽度w0为758.01µm，缝口宽度为919.63µm；以时间120 s 为初始条件进行的漏失速率和漏失体积预测数据与测量数据吻合性高（图14），验证了本文模型的可靠性；在计算过程中仅需钻井液性能（密度和流变性）、测量的漏失速率及漏失体积序列就能计算天然裂缝动态宽度，便于现场应用。