改进时间弹性带的动态避障轨迹规划系统研究

谢春丽,刘斐灏

(东北林业大学 交通学院,黑龙江 哈尔滨 150040)

0 引 言

移动机器人的自主导航中,避障是最关键的功能之一[1]。避障的实时性与稳定性是当前移动机器人路径规划的典型挑战[2]。随着场景的复杂性增加,动态障碍物对于算法的实时性要求增加[3],为在动态环境下生成安全平滑的轨迹,需要轨迹规划算法能够在动态场景下对动态障碍物实时进行轨迹跟踪与运动状态预测[4]。

现有机器人动态避障方法存在对复杂动态环境处理能力不够,易陷入局部最小值[5],且实时性不满足实际应用的需要,且在混合场景下无法准确区分动态与静态障碍物类型[6]。因此动态避障轨迹规划系统需要对复杂环境有较优的处理能力,并能实时求解出可行轨迹[7]。

TEB算法[8]是基于弹性带(elastic bands, EB)[9]方法改进,EB算法使用两个分量来产生避撞路径,即排斥力与收缩力,障碍物施加排斥力在弹性带上形成安全距离,收缩力在避障条件满足的前提下让路径收缩。

TEB算法能够产生一条无碰撞的时间最优化运动路径,对环境中的障碍物进行实时的检测并作出在线规划。动态障碍物环境下,轨迹规划算法需要对环境信息有较优且快速的处理能力,并且能对动态障碍物进行轨迹跟踪与预测[10]。然而,TEB算法在动态场景下会将动态障碍物视为静态去处理,导致机器人在导航过程中与动态障碍物发生碰撞。

针对上述问题,笔者采用不同频率的均值滤波器区分动、静态障碍物,增加动态障碍物代价地图,对障碍物进行聚类处理[11],结合卡尔曼滤波[12]对障碍物的运动轨迹进行跟踪预测,通过预测障碍物轨迹,结合TEB算法规划合理的轨迹进行避障。

1 阿克曼机器人的运动学模型

采取阿克曼转向结构机器人进行仿真与真实实验,阿克曼转向结构机器人的运动学模型如图1。

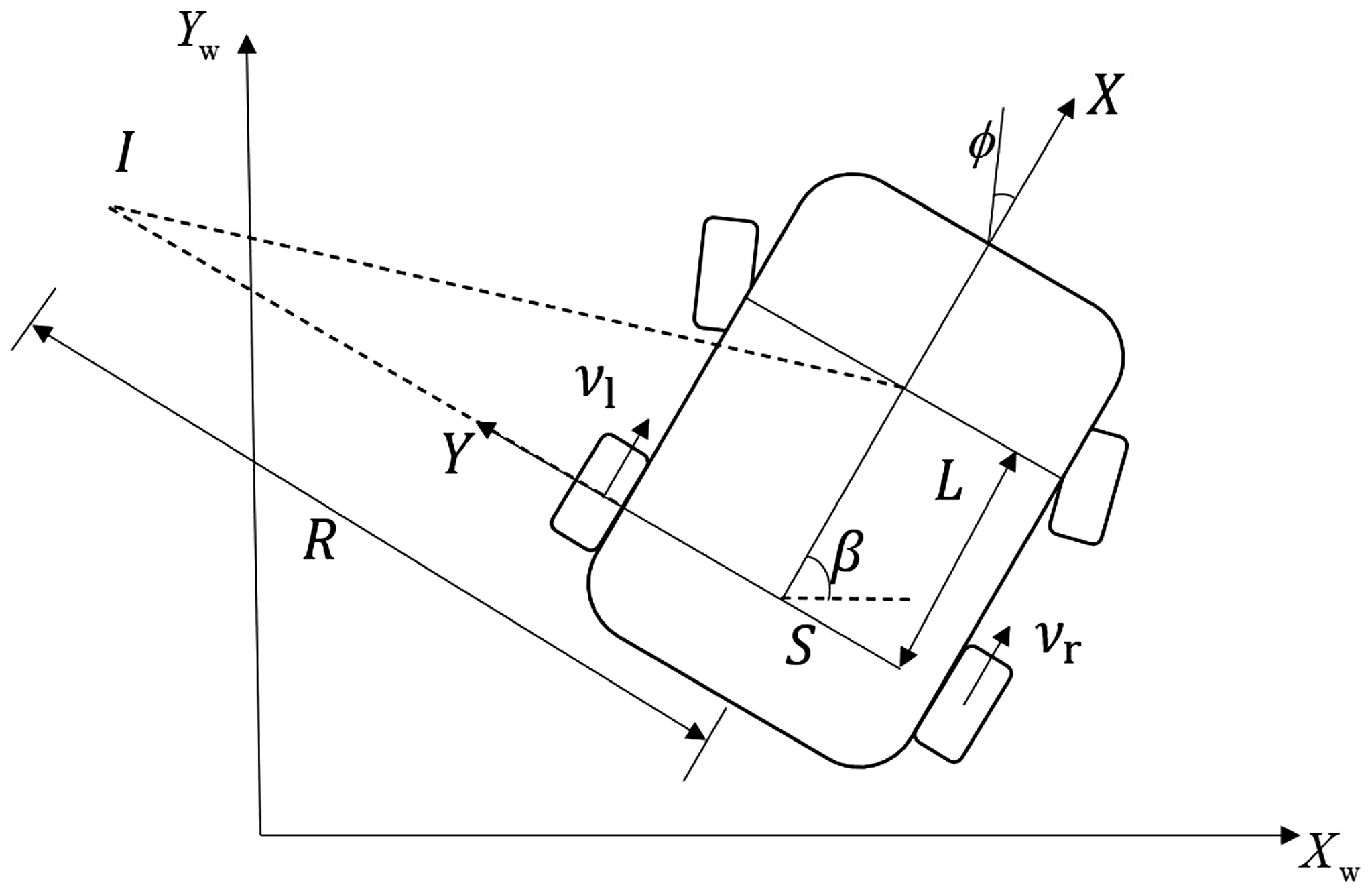
图1 阿克曼转向结构机器人运动学模型

图中(Xw,Yw)为世界坐标系下坐标轴,(X,Y)为机器人基坐标系,坐标原点为机器人后轴中心S点,其中车辆前进方向为X轴正方向,垂直车身向左为Y轴正方向。I点为阿克曼转向机器人瞬时旋转中心(instantaneous center of rotation,ICR) ,φ代表车辆前轮转向角,其中φ∈(-π/2, π/2),R为车辆最小转弯半径,β为车身与世界坐标系横轴夹角。

左、右后轮的平移速度分别为vl、vr,且满足机器人线速度v=(vl+vr)/2。L为轴距,其前轮转向角φ与转弯半径R、轴距L有关,需满足式(1):

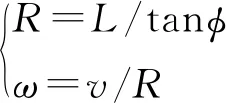
(1)

式中:ω为机器人角速度。

设在t时刻,机器人姿态由位置状态s(t)和运动状态u(t)=[v(t),φ(t)]T表示,则阿克曼机器人运动学状态方程表示为式(2):

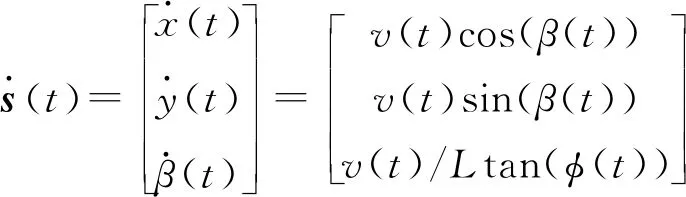
(2)

2 TEB算法原理与求解优化流程

2.1 TEB算法基本原理

TEB算法最初是为移动基础机器人导航规划开发的。通过在弹性带的基础上引入时间因素,增加机器人相邻位姿的时间间隔。因此,机器人的离散运动轨迹T可描述为N个有序的位姿与时间间隔的集合,表示为式(3):

T=[S1,ΔT1,…,Sk,ΔTk,…,ΔTN-1,SN]T

(3)

Sk=[Pk,βk]T,k∈[1,n],Pk={xk,yk}

式中:Sk表示机器人在世界坐标系下的位姿,其中Pk为机器人坐标。ΔTk为位姿Sk过渡到Sk+1的时间间隔。

由连续机器人位姿组成的轨迹示例如图2。

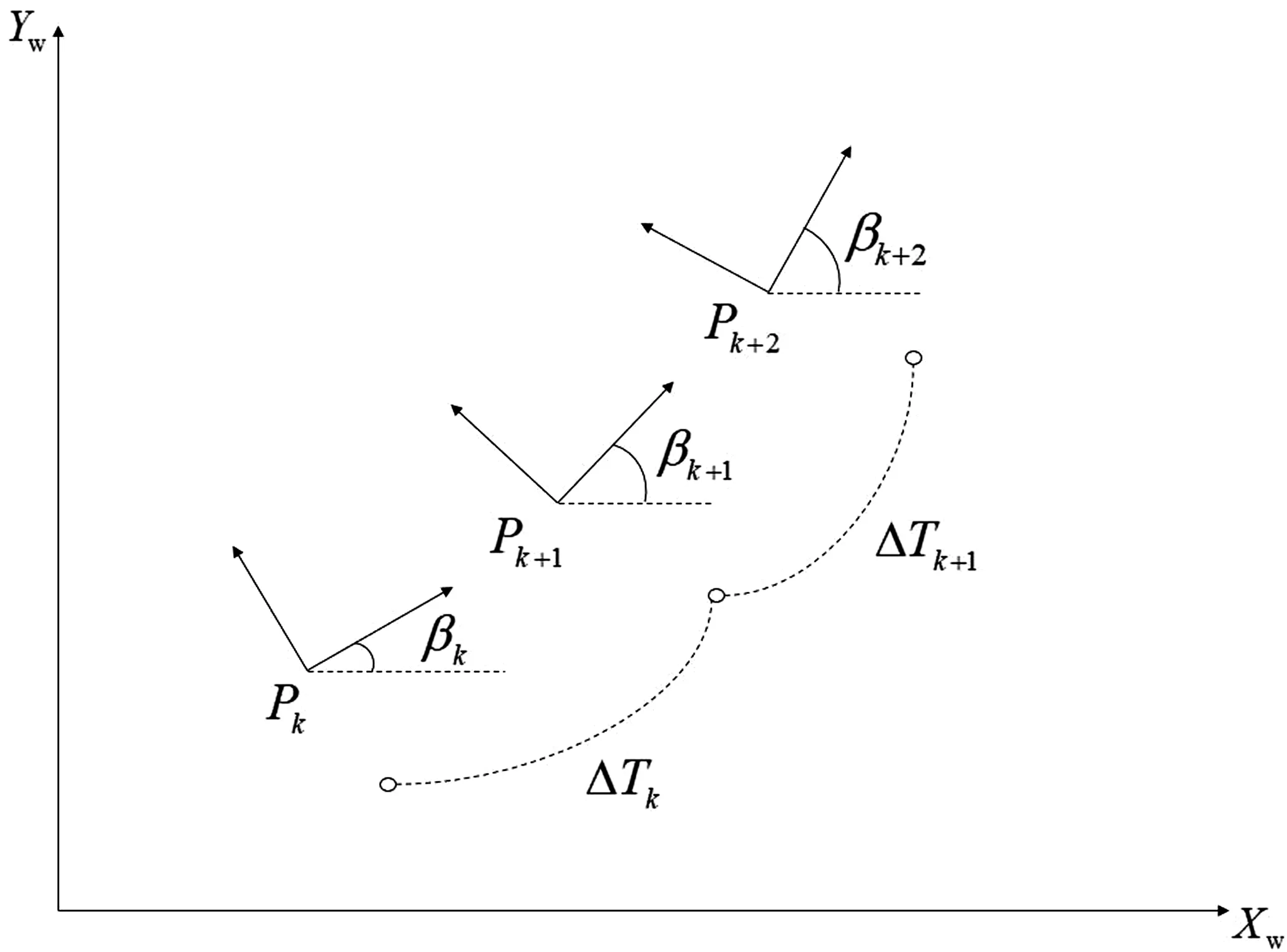
图2 轨迹连续位姿序列与时间间隔

2.2 TEB求解优化流程

在TEB中引入的时间因素将机器人控制系统与速度,加速度等动态约束进行拓展,能够为局部规划器提供一个持续优化的解决方案,在非完整约束移动机器人上得以适用[13],如图3。

通过在局部代价地图中对全局路径的子集进行采样,创建局部姿态序列,将全局路径转变为弹性带进行优化,其生成的路径不一定是最短路径,但能够满足时间最优。在障碍物环境较多情况下,为防止在路径规划过程陷入局部极小值,对具有不同拓扑结构的多条轨迹进行维护和优化,并提出两阶段优化算法解决轨迹局部最优问题[14],而后针对阿克曼转向结构机器人进行拓展[15]。

图3 TEB算法的优化流程

最优轨迹b*是通过最小化代价函数获得,这些函数包括运动规划中的部分冲突目标与约束。这些目标包括CPU资源消耗、路径长度、总运动时间或以上目标函数的加权组合。

通过对不符合移动机器人运动学约束的轨迹加以惩罚函数,将轨迹允许解限制在可行集内。TEB的优化问题被定义为一个加权非线性最小二乘代价函数,该代价函数考虑目标函数J和惩罚函数P的冲突集,表示为:

(4)

式中:b{s1,sN}表示轨迹中的起始位姿s1与目标位姿sN不受优化;σi为每个目标函数的加权因子;fJ为目标函数的综合,目标函数J中包括计算资源,轨迹,运动时间等因素;fP为惩罚函数综合,惩罚函数P包括障碍物约束、非完整运动学约束、速度与加速度约束等。

将TEB优化问题映射到一个超图上,构成解向量的机器人姿态sk和时间间隔ΔTk组成超图的顶点,超图的边由非线性规划的代价项组成。此外,将不受优化的机器人起始和目标位姿、静态障碍物等静态参数作为超图的固定顶点。得到的超图通过g2o框架进行有效求解,该图优化框架利用系统矩阵的稀疏结构,采用了鲁棒性和效率较高的Levenberg-Marquardt(LM)算法求解,计算出各个目标函数与惩罚函数的加权因子,通过最小化代价函数求解出最优轨迹。

3 基于卡尔曼滤波的障碍物运动估计

在ROS的运动规划框架中,代价地图为全局及局部规划器提供实时环境信息。代价地图用一个网格表示,其中每个单元格存在3种状态设定:即空闲(0)、占用(254)和未知(255),代价地图以特定的速度进行更新,但其只能表示静态障碍物的信息。

笔者提出了一个实时的动态障碍物避障策略,使用快速和慢速均值滤波器对二维激光雷达点云数据进行预处理,将动态障碍物从环境中分离出来,完成动态障碍物检测,建立动态障碍物的代价地图层对检测到的动态障碍物进行聚类处理,利用卡尔曼滤波方法,根据当前动态障碍物的运动状态进行轨迹跟踪与状态预测。

3.1 动态障碍物检测

对于代价地图的每一个单元格,使用一个快速运行均值滤波器与一个慢速运行均值滤波器,对机器人前方探测到的激光点云进行预处理。其中单个单元格的滤波器表示为:

Pf(t+1)=(1-αf)Pf(t)+αfC(t)

(5)

Ps(t+1)=(1-αs)Ps(t)+αsC(t)

(6)

式中:Pf(t)、Ps(t)分别为快速运行均值滤波器与慢速均值滤波器在t时刻的输出值;αf、αs为当前代价地图C(t)对均值滤波器的影响程度,且满足0≤αs<αf≤1。

通过两个不同运行速度的均值滤波器对激光点云数据进行高频噪声与低频噪声滤除,实现对动态障碍物占用单元格的识别。快速过滤器激活阈值为c1,快速和慢速滤波器之间的差异必须超过阈值c2,以消除低频噪声的准静态障碍,表示为式(7)、式(8):

Pf(t)>c1

(7)

Pf(t)-Ps(t)>c2

(8)

通过设定阈值操作,障碍物将在代价地图中生成一个二进制映射,即设置动态障碍物、静态障碍物及边界所在单元格标记为1,在代价地图采用不同的颜色表示障碍物类型及边界;自由区域标记为0,设置为空白单元格。

初始代价地图设置如图4,静态层为所建立的环境地图边界,障碍物层包括环境中已有的障碍物及激光雷达实时检测到的静态障碍物,膨胀层是在障碍物外层增加膨胀范围,使机器人在导航过程中能够与障碍物保持更加安全的防碰撞距离。

为优化后的代价地图如图5,通过对实时检测到的动态障碍物激光点云进行分割与聚类,生成动态障碍物层代价地图,并在初始代价地图对应的膨胀层中增加设置动态障碍物的膨胀范围。

图4 初始代价地图

图5 优化后代价地图

3.2 动态障碍物轨迹跟踪与预测

为实现动态避障,机器人感知系统需要对每个动态障碍物的运动参数进行估计与预测。随着动态障碍物运动,激光雷达将获取到的障碍物点云数据上传到可视化端,动态障碍物代价地图层也随之更新动态障碍物信息。将当前代价地图中所占用的单元格与历史代价地图上动态障碍物层单元格进行轨迹分析,构成数据关联问题。

在轨迹跟踪的过程中,新检测的障碍物状态如果能够与多个之前检测的障碍物状态关联,则将过去障碍物的平均状态作为新障碍物平均状态,利用卡尔曼滤波跟踪障碍物的目的就是为了获取障碍物的实时状态,其状态包括位置、速度、方向、障碍物的特征识别。随着采样时间的迭代,卡尔曼滤波器将对动态障碍物的轨迹进行更新预测并加以校正,跟踪过程中动态障碍物状态的所有参数也随着进行同步更新。

动态障碍物在t时刻的位置与运动状态Ot表示为式(9):

Ot=[xt,yt,vx,vy,kt]

(9)

式中:xt、yt为障碍物在t时刻的坐标位置;vx、vy为动态障碍物t时刻投影到x、y轴上的速度分量;kt为障碍物的运动方向。

由此,可得到卡尔曼滤波对于动态障碍物t+1时刻运动状态Ot+1的预测方程如式(10):

Ot+1=AOt+But

(10)

式中:A为状态转移矩阵;B为噪声增益矩阵;ut为过程噪声。

根据传感器获得动态障碍物t+1时刻运动状态测量值与滤波器对系统t+1时刻预测状态,可得到测量值与预测值之间存在的误差以及预测误差协方差矩阵如式(11)和式(12):

o=Z-HOt+1

(11)

Pt+1=APtAT+Q

(12)

式中:o为t+1时刻系统状态测量值与预测值之间存在的误差;Z为传感器传递的状态测量向量;H为观测矩阵,将预测的运动状态向量转换为测量向量相同数据类型;Q为过程噪声协方差矩阵。

得到卡尔曼增益矩阵方程如式(13):

Kt+1=Pt+1HT(R+HPt+1HT)-1

(13)

式中:R为测量噪声协方差矩阵,由于传感器测量只有位置信息,所以此处R为位置的方差。

根据卡尔曼滤波可对动态障碍物运动状态矩阵式(10)以及预测误差协方差矩阵式(12)分别进行更新,表示为式(14)和式(15):

Ot+1=(I-Kt+1H)Qt+1+Kt+1Z

(14)

Pt+1=(I-Kt+1H)Pt+1

(15)

4 实验分析

4.1 仿真实验设置

通过开源仿真平台GAZEBO设置仿真环境(包括静态场景以及动态障碍物),用于验证该算法在动态障碍物场景下避障的有效性。仿真对象为具备阿克曼转向结构的非完整运动学约束机器人,配置的传感器为单线2维激光雷达,IMU(惯性测量单元),里程计。仿真计算机配置:Intel Core i5-4210U,双核四线程,Ubuntu18.04/ROS Melodic。

仿真环境设置:动态障碍物运动设计包括与机器人运动方向垂直,与机器人运动方向同向的两种运动状态。通过仿真实验,分析改进后的算法在面对两种运动方向的动态障碍物时的避障路径,并对机器人避障仿真结果进行分析与讨论。动态仿真环境设置如图6,图中5个作匀速往复运动的动态障碍物中,①②④⑤沿着Xw轴运动,③沿着Yw轴运动。

图6 动态仿真环境设置

为了模拟复杂真实环境与机器人运动,以动态行人及真实轿车尺寸作为参考,其中行人的平均运动速度为3～5 m/s,复杂环境中车辆的前向速度不大于25 km/h。根据仿真场景中,动态障碍物和智能小车的尺寸与运动性能和行人尺寸与真实车辆尺寸、运动性能比较,按照1∶5的比例设置小车与动态障碍物运动参数如表1、表2。

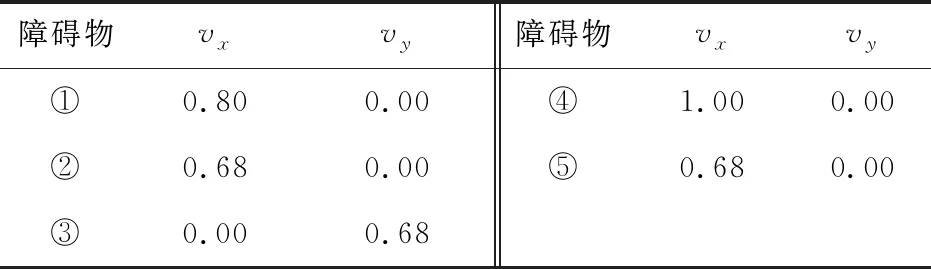
表1 动态障碍物运动参数

表2 机器人运动参数

4.2 全局路径规划算法选择

将全局路径规划算法A*与Dijkstra算法分别和TEB算法组合进行仿真实验,两种算法组合下机器人运动参数设置不变,每个算法组合各进行20次实验。比较不同全局路径规划算法规划的路径长度,路径的平滑度以及机器人运动时间,其中路径平滑度定义如下:通过均匀选取全局路径上的路径点P′,共选取NP′个路径点,计算路径点之间的角速度变化率α,设α> 20%的路径点数量为Nα, 从而按式(16)求得路径平滑度ηsmooth:

(16)

仿真结果平均值如表3。通过对全局路径规划出的路径长度、路径平滑度及机器人运动时间进行比较,选择Dijkstra+TEB的组合算法,其中Dijkstra算法作为全局路径规划算法,TEB算法作为局部轨迹规划算法,该组合算法能够根据起始点与终止点状态以及环境地图信息,求解出两点间最短且更加平滑的路径,实现运动点到点导航任务时间最小化。

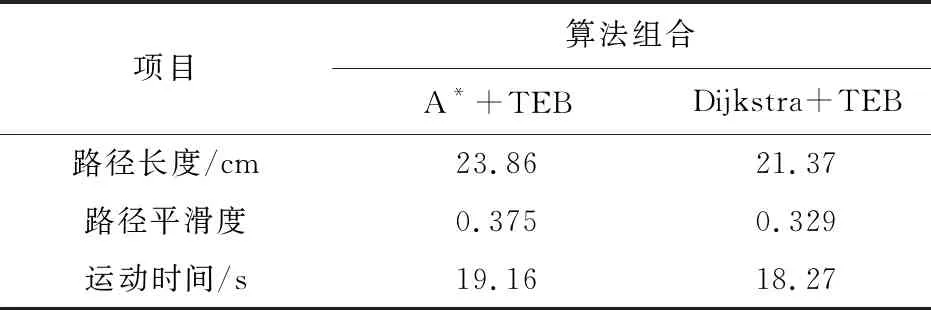
表3 全局路径规划算法比较

4.3 仿真实验结果分析

利用Rviz对仿真结果进行可视化分析。针对动态障碍物与机器人运动方向垂直,以及动态障碍物与机器人运动方向同向,分别进行机器人避障轨迹分析(图7)。2种障碍物运动方向均进行20次仿真测试实验。

图7 机器人避障轨迹

障碍物实际位置如图7(a)中文字描述与箭头指向所示,障碍物周边存在一圈代价地图膨胀层,其余空白区域部分代表环境中车辆可自由运动区域。机器人当前位置、规划的全局路径与局部轨迹以及动态障碍物的当前位置与历史代价地图如图7(a)中文字标注。机器人在沿着全局路径向终点运动时,遭遇到②动态障碍物,根据图中②动态障碍物历史代价地图与当前时刻障碍物位置可知,②障碍沿着Xw轴向其负半轴作匀速运动,此时障碍物运动方向与机器人运动方向垂直。

在当前时刻,机器人沿着根据Dijkstra算法规划出的全局路径向终点运动,局部规划的轨迹如图7(a)。根据障碍物历史代价地图结合卡尔曼滤波,对②动态障碍物的运动轨迹进行跟踪并预测,判断下一时刻②障碍物轨迹会与机器人轨迹存在位置冲突,潜在冲突点如图7(b),故改进的动态避障轨迹规划系统通过对机器人的局部轨迹进行在线优化,生成的优化结果如图7(b)中优化后的局部轨迹,Dijkstra算法根据当前车辆位置重新对全局路径进行最短路径搜索。

机器人沿着根据Dijkstra算法规划出的全局路径向终点运动,当机器人运行到如图7(c)中机器人位置,此时检测到③动态障碍物,同样根据③动态障碍物历史代价地图与当前障碍物的位置可得,③障碍物正沿着Yw向其负半轴作匀速往复运动,且该经过潜在冲突点后会调转方向沿着Yw向其正半轴运动。当前时刻动态障碍物与机器人运动方向为同向。

若按照图7(c)所规划的路径行驶,机器人与③障碍物将在潜在冲突点处会发生碰撞,且由于③障碍物是作往返运动,机器人可能因为障碍物的返回而规划出倒退避让的轨迹,增加了行驶的危险性以及导航运动时间。改进的动态避障轨迹规划系统重新规划处合理的路径如图7(d),优化后的局部轨迹从障碍物上方绕行径,避免在障碍物交汇处陷入局部最优或发生碰撞,此时Dijkstra算法规划的全局路径虽是最短路径,但会导致碰撞。

由以上仿真实验分析可知:改进的动态避障轨迹规划系统能够满足实时动态避障要求及运动时间最优化。经过上述各20次仿真实验,机器人与动态障碍物发生碰撞的次数为3次,其中避障失败的实验中,碰撞发生均出现在动态障碍物代价地图以及周围静态障碍物代价地图出现重合或者交叉时,例如②、③动态障碍物在运动过程中与环境地图发生代价地图的重合,此时机器人尝试求解轨迹而可行域过小导致解陷入局部最优,机器人避让不及导致与机器人发生碰撞。根据结论分析得改进的动态避障轨迹规划系统动态避障成功率为92.5%,该动态避障规划系统可有效对动态障碍物进行实时避障,机器人能成功完成导航并到达目标点。

5 真实动态环境避障实验

实验测试的移动机器人如图8,该移动机器人Nanocar采用阿克曼转向结构,主要传感器配备思岚二维激光雷达,IMU,里程计。车载计算机系统采用微型计算机树莓派4B,4核8线程CPU,频率为1.5 GHz。

图8 真实实验阿克曼转向结构机器人

在真实动态环境中,同样设置与机器人运动方向同向及垂向两种运动状态的障碍物。

图9中动态障碍物运动方向与机器人运动方向为相向,机器人检测障碍物并完成避障的全过程。机器人位置,全局路径以及动态障碍物位置的运动方向如图中标识,其中V0为动态障碍物的运动速度与方向。机器人实时检测到动态障碍物并根据系统的预测作出轨迹规划完成避障的过程。

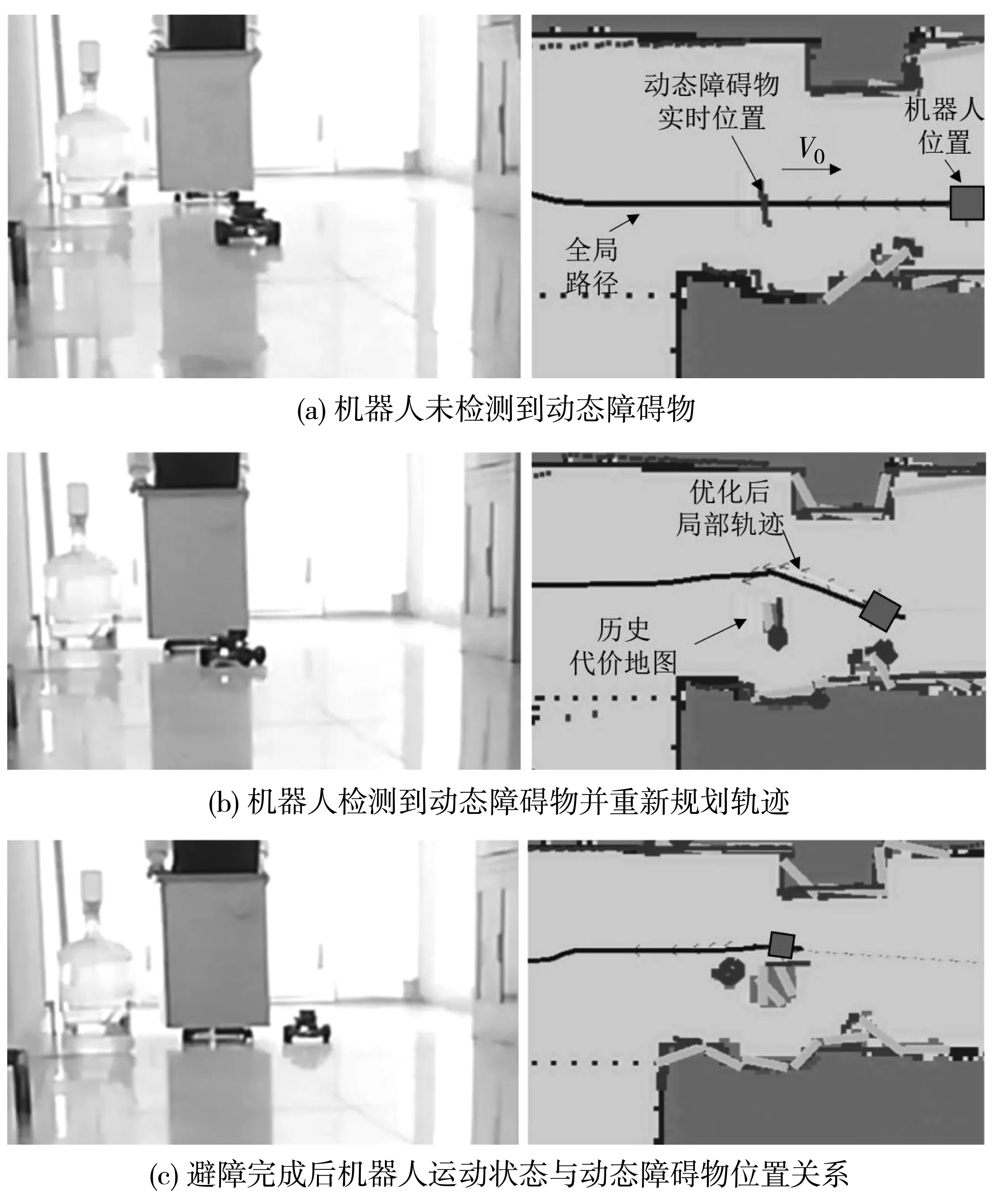
图9 机器人与动态障碍物相向运动场景

图9(a)中,实验员匀速推动柜子作为动态障碍物,但尚未进入机器人轨迹规划算法考虑的范围,此时全局路径与局部轨迹重合;图9(b)中规划系统通过动态障碍物历史代价地图判断出障碍物的运动方向并进行轨迹跟踪,通过预测出障碍物的下一时刻运动状态,实时规划出避让障碍物的运动轨迹;图9(c)为机器人完成动态避障后的运动状态,以及与动态障碍物的相对位置关系。

图10中动态障碍物运动方向与机器人运动方向为垂直。

图10(a)中为当前机器人的位置,动态障碍物的位置及其历史代价地图。图10(b)中,改进的动态避障规划系统对局部轨迹进行优化,选择从动态障碍物右侧通过。图10(c)中显示了避障过程完成后机器人与动态障碍物的相对位置关系。机器人改变路径,避开障碍物成功通过。

在同一环境下进行重复多次实验,验证该动态避障轨迹规划系统能够在实时检测到动态障碍物后,结合历史代价地图,通过卡尔曼滤波进行障碍物轨迹跟踪以及运动状态预测,规划出安全且满足最小化运动时间的平滑避障路径,顺利完成导航任务到达目标点。

6 结 语

针对阿克曼转向结构的移动机器人在动态场景下的实时避障问题,提出了基于改进时间弹性带并结合卡尔曼滤波的动态避障轨迹规划系统。首先对阿克曼转向结构机器人进行运动学模型建立并分析。算法上,通过在时间弹性带算法中增加动态障碍物代价地图层实现动态障碍物的检测,结合卡尔曼滤波对动态障碍物进行轨迹跟踪以及障碍物运动状态预测,从而实时规划出安全的动态障碍物避障轨迹,使机器人能够在复杂动态环境中完成同向及垂向的障碍物运动避障,实现无碰撞导航。

通过设置仿真动态环境以及真实动态场景对该系统进行实验分析讨论。结合可视化软件对动态障碍物检测,轨迹跟踪预测及优化前后轨迹对比,通过实际场景与可视化动态避障过程进行对应,证明了该动态避障轨迹规划系统能够在动态场景环境下实现动态避障,完成导航目标,验证了该系统的有效性。

该系统在TEB中增加动态障碍物代价地图,构建多层代价地图对场景环境进行分解处理,同时仅通过对单线激光雷达采集的点云进行滤波,结合卡尔曼滤波实现动态障碍物的追踪与预测,实现避障完成导航工作。