智能电动汽车自适应巡航分层控制研究

赵树恩,张 亮,甘桦福,陈文斌

(重庆交通大学 机电与车辆工程学院,重庆 400047)

0 引 言

随着环境污染、能源消耗等社会问题日益突出,智能电动汽车以其更高的安全性和更低的能耗被认为是解决上述社会问题的有效途径之一,已成为一个新兴的研究热点[1]。

自适应巡航系统(adaptive cruise control,ACC)作为先进驾驶员辅助系统的关键技术之一,因具备智能化硬件体系,对推进车辆现代化、智能化具有重要意义[2]。近年来,不少研究者对ACC的控制方法进行了研究。为了从整车控制角度实现安全、低能耗驾驶,罗禹贡等[3]提出了一种智能混动车辆自适应巡航分层控制体系,上层控制融合了纯电动驱动和发动机驱动的双模式切换自适应巡航控制,中层控制整车状态识别及转矩分配控制,下层控制为驱动制动系统协调控制,通过实车试验验证了控制方法的有效性;CHENG Shuo等[4]提出了一种基于博弈论的纵向自主驾驶控制框架,比现有的基于模型预测控制算法具有更高的能量效率和更好的纵向控制性能。针对车辆纵向时变非线性运动的不确定性,尹智帅等[5]设计了一种基于粒子群优化的纵向自适应径向基神经网络控制器;初亮[6]基于迭代学习方法设计了自适应巡航驱动和制动控制算法,仿真结果表明,PID控制方法与迭代学习控制方法的跟随效果相近,但迭代学习控制下的制动和驱动控制更加平稳;张亮修等[7]建立整车14自由度模型,基于线性二次型最优控制原理求解期望加速度,设计模型匹配控制器,使车辆在加速行驶、稳态跟车、制动减速工况下保持良好的跟踪性和自适应性。为了减少计算量,传统线性二次型最优算法(linear quadratic regulator, LQR)的权重矩阵均取固定的经验值,但车辆行驶速度变化范围太大时,控制效果不佳。李想[8]基于模糊控制原理对线性二次型最优控制算法进行改进,实现了权重矩阵的动态取值,同时具有较好控制精度与舒适性。然而多数研究是采用固定跟车距离[9]或者时间间隔策略[10],这样会使一些驾驶员的驾驶体验不佳[11]。为提高ACC系统使用率,使ACC跟车特性与驾驶员驾驶风格兼容,S.M.MOHTAVIPOUR等[12]引入了新型正弦和高斯函数的非线性参考模型,使跟车距离大时提供更高速度并在跟车距离小时采用保证安全的更平滑变化的函数。而跟车时距的选择对交通流稳定性和道路通行能力也有很大影响,在高速行驶时,固定车间时距会导致过大车间距,使道路通行能力降低,难以适应复杂多变的环境[13]。D.YANAKIEV等[14]提出的可变车间时距能引导更大的交通流,适应交通流量变化,但前车频繁加减速时控制效果不好。基于此,翟志强等[15]设计了考虑前车加速度变化的可变车间时距策略,仿真结果表明,该策略能较好地适应前车频繁加减速。然而,以可变跟车时距策略作为期望跟车距离时,基于经典线性二次型控制框架,寻求的最优反馈系数矩阵不能反映车间时距变化对决策加速度的影响,因此需要对线性二次型控制算法进行改进。

针对纯电动车自适应巡航的工作速度受前车速度变化影响而跟踪性差的问题,笔者以分布式动电动汽车为研究对象,利用分层控制的思想对智能电动车自适应巡航控制进行研究。首先,采用可变车间时距策略作为期望跟车间距,基于经典线性二次型最优控制理论,利用四次多项式拟合法分析不同车间时距引起最优反馈增益的非线性变化,为保证智能电动车能准确跟踪前车速度并保持安全距离,综合考虑相对距离误差、相对速度以及自身车辆加速度,建立基于改进线性二次型最优控制的上层控制器,以决策出期望加速度;然后,下层控制器应用分数阶PID控制理论,对期望驱动力矩和制动压力进行跟踪,为使控制更准确,利用Oustaloup算法实现分数阶微分算子的近似,采用遗传优化算法对ITAE性能指标寻优整定FOC参数,以确保控制系统的稳定性和精确性;最后,运用MATLAB/simulink与CarSim联合仿真对该控制方法进行验证。

1 自适应巡航控制运动学建模

ACC是一种智能化的自动控制系统,它是在早已存在的巡航控制技术的基础上发展而来的。在车辆行驶过程中,安装在车辆前部的车距传感器持续扫描车辆前方道路,同时轮速传感器采集车速信号。当与前车之间的距离过小时,ACC控制单元可以通过与制动、驱动系统协调动作,以使车辆与前方车辆始终保持安全距离。纵向跟车时的车辆间运动学关系如图1。

图1 车辆间运动学关系

纵向安全距离是巡航过程中防止车辆碰撞的关键因素之一。为适应前车加减速的变化和保证交通流稳定性,采用可变车间间距策略[15]:

ds,e=vsth+d0

(1)

(2)

式中:ds,e为期望安全距离;vs为自车速度;d0为两车静止时的最小距离,d0=1～3 m;th为车间时距,在1～2.5 s之间取值;t0、c1、c2为大于0的参数,分别取1.5 s、0.05、0.3;Δv为两车相对速度;af为前车加速度。根据车间纵向运动学关系,将跟车间距误差Δd和相对速度Δv定义为:

(3)

式中:d为实际车间间距;vf为前车车速。

由于执行机构动作使实际加速度响应滞后,则实际自车加速度与期望的自车加速度关系采用一阶惯性延迟表示:

(4)

式中:Kl为系统增益;τl为时间延迟;as为自车实际加速度;ae为期望加速度。

选择系统状态变量x=[ΔdΔvas]T,控制变量为u=[ae],干扰变量为w=[af],状态空间模型为:

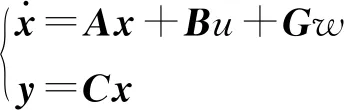
(5)

用rank[BABA2B]来检验状态空间可控性。经计算得,rank[BABA2B]=3为满秩矩阵,根据系统可控性准则,判断系统是可控的。

2 智能电动车自适应巡航分层控制器设计

笔者设计的智能电动汽车自适应巡航系统的控制结构框架如图2。在上层控制中,以相对距离误差、相对速度和自车加速度为输入,考虑线性二次型最优控制增益非线性变化的问题,先对反馈增益值进行多项式拟合,而后决策出加速度;下层控制应用分数阶PID理论,对期望驱动转矩和制动压力进行跟踪控制,从而使自车能够准确快速地跟踪上前车。

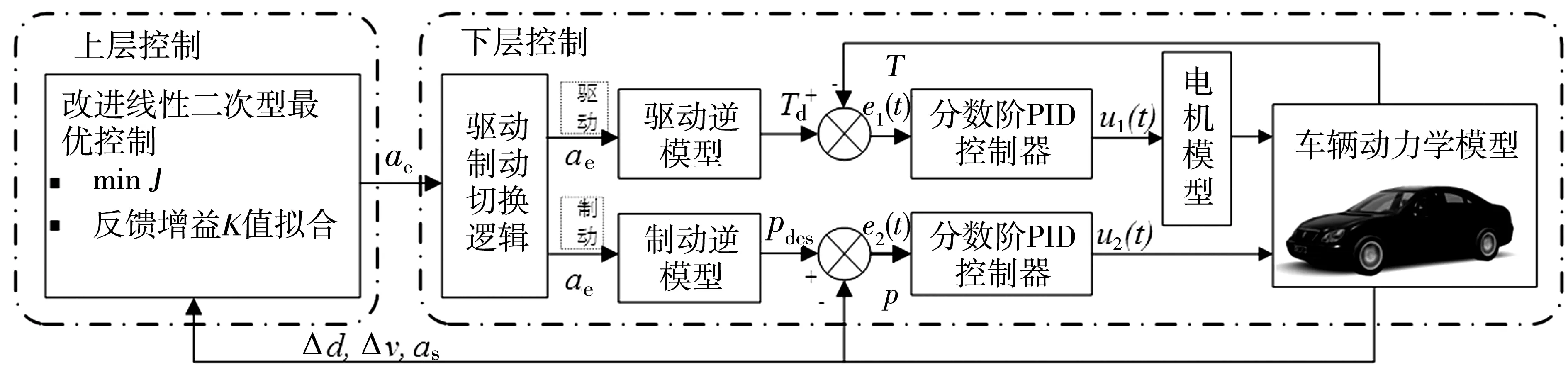
图2 智能电动汽车自适应巡航系统分层控制架构

2.1 基于改进LQR的上层控制器设计

纵向安全距离采用了可变时距策略以适应复杂多变的行车环境,但传统LQR的最优固定反馈增益无法响应车间时距的变化,使得决策出的加速度不满足跟车需求。因此,上层控制综合考虑车距误差、相对速度以及自车加速度,利用多项式拟合法量化分析不同车间时距对反馈增益的影响,对LQR进行改进,将性能指标函数最小时的加速度作为期望加速度。

在跟车工况中,两车间期望间距误差Δd与两车相对速度Δv越趋近于零,则稳定性越好,安全性越高。因此,可以建立考虑间距误差、相对速度、自车加速度的性能指标函数,其性能指标为:

(6)

式中:x为状态变量;Q、R为状态变量和控制输入的加权系数矩阵,取经验值。

根据最优控制,存在使性能指标极小的唯一状态,线性反馈的最优控制律,如式(7):

u*=-R-1BTPx=-K1×3x

(7)

ATP+PA-PBR-1BTP+Q=0

(8)

式中:P为黎卡提方程的稳态解,可通过求解式(8)得到;K1×3=-R-1BTP为状态反馈增益矩阵,K1、K2、K3分别为K1×3的3个元素。

由式(1)、式(5)、式(7)、式(8)可知,不同的th取值使最优反馈增益矩阵K1×3呈非线性变化,从而引起决策加速度变化。但传统LQR的反馈增益矩阵K1×3为固定值,不随th改变,使得决策出的期望加速度无法响应前车速度变化。因此,采用多项式拟合的方法量化分析不同车间时距对反馈增益矩阵的影响。th取值为1～2.5 s,以间隔0.1 s离散化th,求解离散th对应的固定控制增益矩阵。通过计算发现,K1不受th影响。对K2、K3进行多项式拟合,表达式为:

(9)

式中:P(i)为K2多项式拟合系数矩阵中的第i个元素,i=1,2,3,…,5;O(i)为K3多项式拟合系数矩阵中的第i个元素;j为多项式次数,j最大取5。

分别用二次至五次多项式对K2、K3值进行拟合,拟合结果曲线如图3(a)、图3(b),不同的th取值使K2、K3呈非线性变化。在图3(a)中,K2的二次多项式拟合曲线不能很好地贴合原始值,三次、四次和五次多项式曲线逼近离散点,拟合效果相对于二次拟合曲线较好;图3(b)中,K3的二、三次多项式拟合曲线不能很好地贴合原始值,四次和五次多项式曲线可以很好地逼近离散点。综合考虑拟合精度和计算效率,选择四次多项式作为最后的拟合曲线。图3(c)中K2,K3的拟合残差最大不超过0.000 15,说明四次多项式曲线拟合精度高,效果较好。

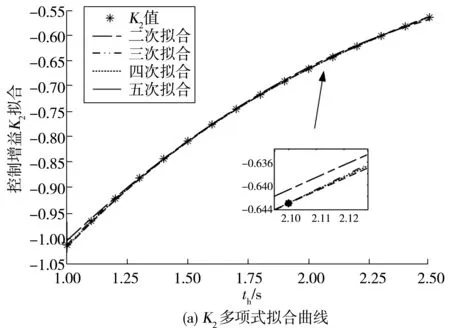
图3 反馈增益K2,K3四次多项式拟合结果

将拟合后的K值多项式代入式(7),则最优控制律可以表示为:

(10)

同时,为保证乘坐舒适性,对跟踪的期望加速度进行限制,使ae取值在-3～3 m/s2范围内。

2.2 基于分数阶PID的下层控制器设计

下层控制中,应用分数阶PID控制器对由逆动力学模型得出的期望驱动转矩和制动压力进行跟踪控制,以实现对整车加减速的控制。分数阶PID控制器对其本身参数和系统参数的变化并不敏感,相比于PID控制器有更强的鲁棒性[15]。

2.2.1 驱动制动切换策略

为提高智能电动汽车的能量效率和维持机械系统的寿命,应避免驱动力矩和制动力矩同时出现[17],所以制定驱动制动切换策略。忽略坡度阻力,则车辆的纵向动力学方程为:

(11)

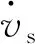
将驱动机构和制动机构都不工作时的车辆减速度作为滑行减速度a,由于存在空气阻力,滑行减速度受到车速的影响而发生变化。取电机牵引力矩和制动压力为0时,以平稳干燥路面下不同速度的最大滑行减速度建立查询表,确定驱动制动的逻辑切换曲线。简单的逻辑判断为期望加速度与滑行减速度的差值大于零则驱动,否则制动,但切换操作频繁,舒适性较差。为提升乘坐舒适性,在切换曲线上下设置一个过渡区域Δh,切换逻辑如表1。

表1 驱动制动切换逻辑

2.2.2 期望驱动力矩跟踪控制

对于分布式驱动电动汽车,由4个轮毂电机分别驱动车轮,因为主要在整车层面研究车辆动力学问题,所以在建立电机模型时不考虑电机内部的运动特性。那么,电机输出转矩可以用忽略延迟的一阶传递函数表示:

(12)

式中:τ为时间常数;Tmr为电机的牵引力矩。

当驱动制动切换策略判断为驱动时,忽略空气阻力的影响,则通过纵向动力学模型计算出期望驱动转矩:

(13)

由于电机输出的能量直接作用在轮胎上,单个电机期望的牵引转矩可以表示为[17]:

(14)

为了保证对期望转矩进行快速跟踪,应用分数阶PID对驱动转矩进行控制,其控制律为:

(15)

理论上,分数阶系统是无限维的,不能直接采用整数阶的控制方法。笔者采用Oustaloup滤波器近似方法来逼近分数阶微分,设定频率段为[w1,w2],则滤波器传递函数可以写为

(16)

式中:H为连续滤波器的增益;w′k为零点;wk为极点;N为滤波器的阶次。

为使分数阶PID控制器设计合理,则需对其中参数kP、kI、kD、λ、μ进行优化。应用较广泛的单纯形法和专家整定法具有初值敏感和规则复杂等缺点,而遗传算法因其具有直接对结构对象进行操作、不存在求导和函数连续性的限定特点,且具有内在的隐并行性和更好的全局寻优能力,因此选取遗传算法进行参数寻优。遗传算法包括产生群体、计算适应度值、再生、交叉、变异等操作。

为确定一组合适的kP、kI、kD、λ、μ参数,使性能达到最优,选取ITAE性能函数作为适应度函数,公式定义为:

(17)

利用MATLAB遗传优化工具箱,采用二进制编码,初始种群大小设为100,迭代次数设为200,个体变量为5,交叉后代比例为0.75,变异率为0.05。对参数设置选取限制范围:kP1∈[0,100],kI1∈[0,100],kD1∈[0,100],λ和μ过大或者过小都会使控制器的稳态精度和稳定性下降,所以λ,μ∈[0,2]。在遗传算法运行过程中,种群不断进化,最终得到最优个体适应度函数值变化曲线以及最优个体值。

2.2.3 期望制动压力跟踪控制

当驱动制动切换策略判断为制动时,车辆在减速过程中期望制动压力表示为:

pdes=Tb/δ

(18)

(19)

式中:δ为比例制动系数。

采用分数阶PID控制器对制动压力进行跟踪控制,控制律u2(t)可以表示为:

(20)

式中:e2(t)=pdes-p为期望制动压力和实际制动压力的误差;kP2、kI2、kD2分别为比例、积分、微分控制参数,采用遗传算法求得。

3 仿真分析

利用CarSim与MATLAB/Simulink联合仿真,前车在如图4的2种工况下行驶,对设计的智能电动汽车自适应巡航控制系统的有效性进行验证。

图4 仿真工况

3.1 前车正弦加减速工况

设定前车和自车的初始车速为40 km/h,初始车间距为18.7 m,从t=0开始,前车的加速度变化规律遵循正弦曲线af=0.5sin0.2πt+0.2。

图5展示了在前车正弦加减速工况下,自车车速跟随、车间距跟随和加速度跟踪控制效果。从图5(a)可以看出,正弦工况下的期望相对距离曲线可以反映出前车速度的变化,而车间距跟随的平均绝对误差为0.343 4,均方根误差为0.433 7,这表明实际相对距离足够接近期望相对距离,车间距跟随效果较好。由图5(b)可知,自车速度先随着前车加速而加速,在前车减速时,也能迅速响应。由表2可知,车间距跟随的平均绝对误差为0.343 4,均方根误差为0.433 7,即车速跟随和车间距跟随的总体偏差较小,表明两车基本维持在一个期望的安全距离,具备较好的安全性能。图5(c)中的加速度为平滑曲线,未出现抖震现象,期望加速度曲线与前车加速度曲线基本吻合,决策的期望加速度随前车加速度呈正弦变化,同时,自车实际加速度可以稳定快速地跟踪上期望加速度,表明基于分数阶PID控制建立的下层控制器可以快速响应,跟踪效果好,稳定性好。

图5 正弦工况仿真结果对比

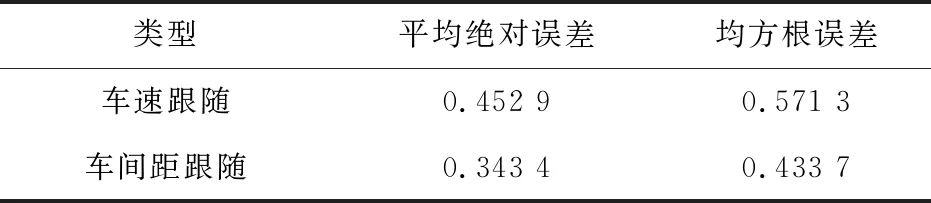
表2 前车正弦工况下的车速和车间距跟随误差

3.2 前车阶跃加减速工况

如图4,前车首先以40 km/h匀速行驶7 s,在7～20 s匀加速至86.8 km/h,然后匀速行驶5 s,在25～35 s匀减速至58 km/h,接着匀速行驶5 s,在40～55 s匀加速至74.2 km/h,最后匀速行驶5 s。

图6(a)～图6(c)为在前车阶跃加减速运动工况下,车速跟随、车间距跟随和加速度跟踪曲线。从图6(a)和表3可以发现,车间距的平均绝对误差为0.457 8,均方根误差为0.610 2,即车速跟随和车距跟随的总体偏差较小,车间距始终接近期望车间距。从图6(b)可以看出,当前车加减速时,自车也能相应加减速,表明建立的ACC控制器能够快速响应前车的变化。由表3可知,车速跟随的平均绝对误差为0.655 0,均方根误差为0.869 3,表明在阶跃工况下,自车也能准确地跟随前车向前行驶。在图6(c)中,当前车加速度在7 s突变为1 m/s2时,自车随前车的变化迅速响应,并保持相应的变化,然后在30 s进行减速行驶时,自车跟随相应变化,可以看出,车辆整体控制良好,系统功能实现良好,具备较好的安全性能。

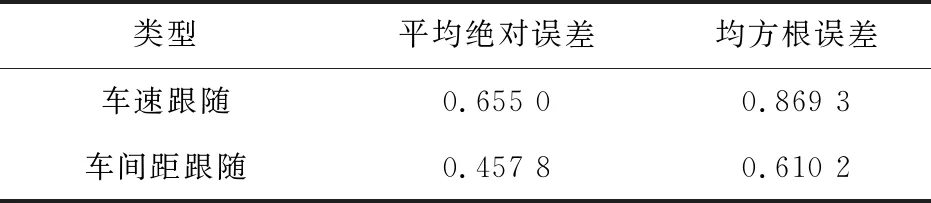
表3 前车阶跃工况下的速度和车间距跟随误差

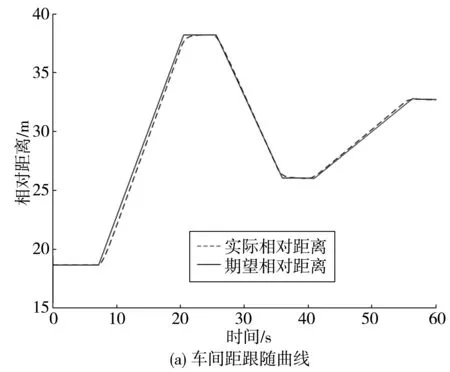
图6 阶跃工况仿真结果对比

4 结 语

笔者应用分层控制的思想建立分布式驱动电动汽车自适应巡航控制策略。首先,在上层控制中,采用可变车间时距策略作为跟车间距策略以适应前车加减速变化,考虑经典线性二次型最优反馈增益非线性变化问题,利用四次多项式拟合方法量化分析不同车间时距对反馈增益矩阵的影响,对线性二次型进行改进,使得输出的期望加速度响应车间时距的变化;然后,基于分数阶PID控制理论建立下层控制器,并利用遗传算法对控制参数进行优化,以实现对期望驱动转矩和制动压力的准确、快速跟踪,使得智能电动汽车与前车保持一个合适车间距的同时,保证安全性,又能够满足目标车速要求,跟车性能较好。

城市行车环境复杂,车速变化频繁,而可变车间时距策略能更好的适用于城市行车工况。但城市路口数量众多,仅仅考虑前车速度可能会造成安全事故,因此,在后期的研究中会对城市交叉路口的自适应巡航控制策略进行研究。