城市快速路互通立交交织区长度可靠性设计

张 航,段和柱,储泽宇

(武汉理工大学 交通学院,湖北 武汉 430063)

0 引 言

互通立交交织区作为城市快速路系统的重要组成部分,是发挥交通功能的瓶颈区以及交通事故的多发区。当城市快速路互通立交的匝道出入口间距不能满足规范要求时,通常需要在相邻入口和出口间增设辅助车道,互通立交区域内的车辆会在辅助车道及相邻车道间发生交织行为,这要求该辅助车道最小长度应符合车辆完成车道变更行为所需要的距离(即该辅助车道的长度需要满足交织区的长度),并与城市快速路整体的道路通行能力相适应。若交织区长度过小,会严重影响城市快速路的道路通行能力,甚至造成交通事故;若交织区长度过大,虽然可以提高互通立交整体的通行效率,但会导致占地面积大且工程造价更高。因此,应从交通安全、道路通行能力等角度综合考虑来确定合理的交织区长度。

目前,学者对城市快速路交织区内的通行能力以及交织区长度广泛的研究。周荣贵等[1]通过对国内城市快速路交织区通行能力的研究分析,并借鉴和吸收美国HCM2010交织区运行分析方法的相关规定,出版了《公路通行能力手册》(简称《手册》);周晨静等[2]以实测数据为基础对《手册》中交织区内的速度计算模型进行了适用性分析,发现模型在城市快速路中同侧交织区拟合度较高。上述研究发现,《手册》中借鉴美国HCM2010交织区的相关方法进行参数标定和修正所用的实测数据均来自城市快速路交织区,因此《手册》中交织区的相关分析方法普遍适用于城市快速路交织区,但当城市快速路交织区出现过饱和交通流、交织区限速、交织区应用智能交通系统、下游堵塞或需求匮乏、多重交织区等情况时,《手册》中交织区的相关方法将不再适用。

孟祥燕[3]把交织区长度作为通行能力的主要影响因素,建立交织区通行能力线性优化模型,得出不同交织区长度时对应的通行能力值;徐艳等[4]通过建立以密度为指标评价交织区服务水平计算模型,得到满足某一服务水平和交织流量下所需的最小交织区长度。这些研究均是基于实例进行分析,得到满足某服务水平下交织区长度和交织区总流量之间关系,从而得出相应的交织区长度。在研究交织区高效运行、相关道路指标取值满足规范的同时,该道路指标是否能保证其设计安全,且安全水平有多高,在现阶段所有规范中均未具体的说明且缺少直接方法确定交织区长度。特别是交织区长度在CJJ 37—2012《城市道路工程设计规范》[5](简称《规范》)中只给出相对范围(150～750 m),对相应设计速度下的交织区长度未给出明确值,因此当受到道路条件限制,设计人员往往凭经验确定交织区长度时,其设计指标的预期安全效果将会不太明确。F.P.D.NAVIN等[6]最先将可靠性理论引入到道路工程中去,并采用相关案例进行说明。游克思等[7]通过构建基于质点模型的侧滑失效功能函数,评价了车辆在曲线段的安全可靠性。仉文岗等[8]运用可靠度理论相关知识对隧道的施工过程以及运营过程展开分析。

鉴于此,笔者将结合可靠度理论知识,对交织区长度进行安全可靠性分析,采用可靠度指标和失效概率将交织区长度安全可靠性进行量化研究。同时基于现有研究成果及《手册》交织区中的相关方法,构建交织区长度计算模型;结合可靠度理论知识,依托交织区长度计算模型,建立可靠度功能函数;在不同设计速度下用该函数检验《规范》中最小交织区长度的可靠性;并用可靠度指标和失效概率对该指标进行评价;在满足三级服务水平的条件下,根据城市快速路所采用的目标可靠指标,反算得出不同设计速度下相对应的交织区长度推荐值。

1 互通立交交织区长度确定

1.1 互通立交交织区安全分析

A型交织区是我国城市快速路互通立交中最为典型交织构型如图1,其中A型交织区主要分布在互通立体交叉中的苜蓿叶立交、环形立交的匝道出入口间及快速路主辅路的出入口间。根据《手册》中对A型交织区的分析,驾驶员为到达期望车道至少需进行一次车道变更行为[5]。在A型交织区内,交织车辆的车速、道路通行能力及安全可靠性均会随交织区长度增加而提高。在交织区总流量及交织流量比一定的条件下,主线为双向四车道的交织区内可实现路径变更的车道数最少,其道路通行能力也最差[5]。因此,A型交织区内,在主线车道设计为单向两车道,辅助车道为单车道(即交织区内可用的交织车道数为3的情况下)这种最不利的条件下,计算所得到的交织区长度在应用时最为安全。

图1 A型交织区

根据《规范》可知,当主线设计速度为100 km/h时,在交织区总流量以及交织流量比相同的情况下,其满足所需服务水平的交织区长度最长,这表明设计速度越大,越不利于交织车辆完成变更路径行为,所需的交织区长度越长。根据实地调查数据,交织车道数为3的A型交织区的最大交织流量比为0.45。由《规范》可知,城市快速路基本路段交通安全、顺畅行驶的要求是满足三级服务水平,由于《规范》中未对交织区的服务水平和交通密度做出特殊规定,因此交织区内服务水平标准也采用三级服务水平(采用三级服务水平上限值进行研究,即每车道车流密度为32.0 pcu/km),这样做也是偏于安全的。则可根据在满足三级服务水平的条件下,可求得交织区中最大服务交通量,结果见表1。

表1 互通立交交织区基本数据设定

1.2 城市快速路交织区长度计算模型

《规范》中规定交织区长度为150～750 m。规范认为,在城市快速路系统中若交织区长度低于150 m,此情况与无信号交叉口类似,可视为无信号交叉口做出研究分析;若交织区长度高于750 m,此情况下车辆有足够机会去完成交织所需的车道变更行为,相当于一般路段变更车道现象,与基本路段无明显差别。笔者研究了《规范》中所提供的最小交织区长度在道路设计中的安全可靠性,并在给定服务水平条件下,反算出不同设计速度下相对应的一个交织区长度推荐值,供在城市快速路互通立交确定合理的交织区长度设计进行参考。图2为城市快速路互通立交交织区长度计算流程。

结合我国城市快速路实际情况,将道路服务水平(车流密度指标)作为约束条件,在上述分析最不利的情况下构建出交织区长度计算模型,利用MATLAB进行脚本代码的编写来实现该模型的计算。具体建模思路为:

根据《手册》交织区相关公式,推导出交织区长度的计算公式,在三级服务水平的条件下,求得该交织区内的最大交通流量,输入A型交织区最不利交通参数,得到对应于某一车流密度下的交织区长度。

图2 城市快速路交织区长度计算流程

根据以上思路,城市快速路交织区长度的计算模型如下:

1)交织强度系数Wi

(1)

式中:Q为交织区总流量,pcu/h;Qr为流量比;L为交织区长度,m;N为交织区内总车道数;a、b、c、d为标定的常数,可参照《手册》,如表2;Q为交织区总流量,pcu/h。

当i=w时,即Ww为交织车流交织强度系数;当i=nw时,即Wnw为非交织车流交织强度系数。

表2 计算交织强度系数时的常量

2)交织与非交织车速Vi

(2)

式中:VFF为基本路段的平均自由流速度,km/h。

当i=w时,即Vw为交织车辆区间平均速度,km/h;当i=nw时,即Vnw为非交织车辆区间平均速度,km/h。

3)交织区速度V

(3)

式中:Qnw为交织区非交织流量,pcu/h。

4)车流密度K

(4)

5)交织区长度Ls

(5)

城市快速路交织区路段内交织区总流量可以分为4种方向的OD需求,即Q=QFF+QFR+QRF+QRR,如图3。

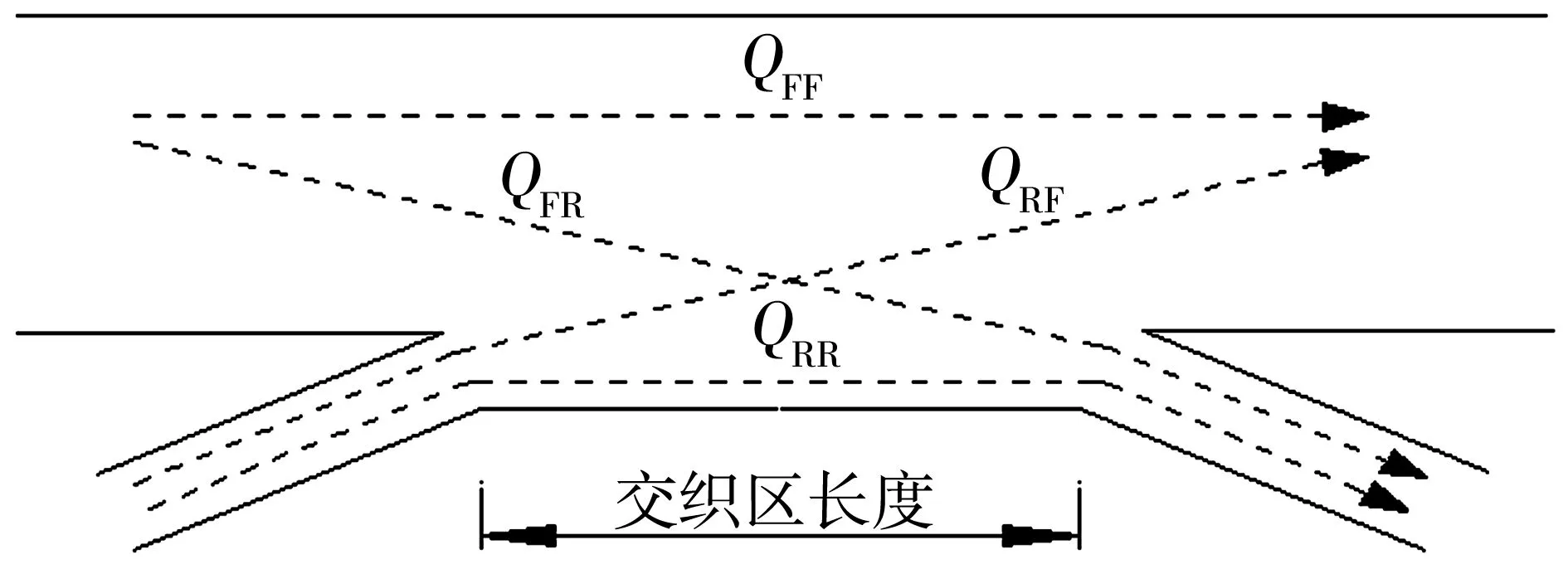
图3 交织区内OD需求

主线到主线(freeway-to-freeway,FF),流量为QFF;主线到匝道(freeway-to-ramp,FR),流量为QFR;匝道到主线(ramp -to- freeway, RF),流量为QRF;匝道到匝道(ramp-to-ramp,FR),流量为QRR。通过不断调整各种流向的流量即可得到应用于不同类型城市快速路交织区长度的计算模型。如输入交织区总流量时QRR=0,而其他流向的交织区流量不变,可得到只进不出的城市快速路互通交织区长度计算模型;输入交织区总流量时QRF=0,其他流向的交织区流量不变,可得到只出不进的城市快速路互通交织区长度计算模型。

2 基于可靠度理论的交织区分析

2.1 建立可靠度功能函数

交织区长度的作用,在于让交织车辆的驾驶员在有限的时间和空间内实现行驶路径变更,到达自己的期望车道[9]。交织区长度可靠性分析在应用可靠性理论知识时可阐述为:当交织车辆的驾驶人在交织区进行行驶,车辆需要在有限的交织区长度内实现行驶路径变更,为使得驾驶员能够按照自己的期望车速进行车道变换,需要有合适的交织区长度,这个交织区长度就是驾驶人驾驶汽车行驶在道路上为保证行车安全所需的交织区长度,可视为可靠性理论中的需求(与结构中的荷载效应相类似);而由道路为驾驶人所提供的交织区长度,在笔者研究中取规范中的下限(与结构中的抗力相类似)。因此,根据可靠度相关理论,可用式(6)描述交织区长度的可靠度功能函数C:

C=f(L)=LR-LS

(6)

式中:LR为交织区长度在《规范》中的范围下限值;LS为保证行车安全所需的交织区长度。

在可靠度理论中通常采用可靠概率Ps、失效概率Pf、可靠指标β来进行衡量。β与Ps、Pf这3项指标具有一一对应的关系,即可靠指标β越大,可靠概率Ps越大,失效概率Pf反而越小。

2.2 可靠度功能函数参数分析

可靠度功能函数中涉及的变量较多,现将交织车辆区间平均速度、交织区基本路段的平均自由流速度作为随机变量。

a、b、c、d与交织类型有关,确定其类型后,可将之作为确定性变量;在分析确定交织区中车道数的最不利情况是在约束运行的条件下,主线为单向双车道,辅助车道为单车道的形式,且根据实地调查数据,三车道A型交织段的最大交织流量比为0.45,即Qr=0.45、N=3;Q交织区总流量则是根据所对应道路服务水平等级求得最大交织流量。因此,以上这些变量均可视为确定性变量。

目前,大多数研究认为在城市快速路交织区内,交织车辆区间平均速度、交织区基本路段的平均自由流速度基本服从正态分布。经过对武汉市快速路交织区进行实地调研,利用雷达微波监测数据。监测参数包括以车道为基础的流量、速度等。在进行交织区选择时,应选择与研究对象相一致的带有辅助车道的典型A型交织区,以及能够较好的监测出交织区及与其相连的入匝道、出匝道交通流数据的地点。将采集到的城市快速路交织车辆区间平均速度和交织区基本路段的平均自由流速度作为统计样本,经SPSS软件K-S检验得到以下正态参数,如表3。

表3 运行速度统计正态参数

2.3 交织区长度可靠度

通过对以上各变量的研究与分析,采用式(6)建立交织区长度可靠度功能函数,检验我国现有规范中最小交织区长度的可靠性。目前,用可靠度理论知识结合城市快速路相关的设计研究较少,《规范》中没有对在城市快速路中的可靠度应用做出明确规定,一般来讲,由于交织区长度不足引发交通冲突频发程度,及车辆行驶的安全情况受到威胁程度与由路面结构引发的事故程度相近,因此可以借鉴JTG 2120—2020《公路工程结构可靠性设计统一标准》[10]中对路面结构目标可靠度的规定,应用于笔者模型进行求解,如表4。

表4 不同城市道路等级的目标可靠性

现在以主线设计速度为100 km/h时,对最小交织区长度可靠度进行分析为例展开计算。

在Qr=0.45时,假设该城市快速路交织区每车道车流密度K=32.0 pcu/km,根据道路服务水平和最大交通流量一一对应的关系,可知该交织区的最大交织流量为4 480 pcu/h。交织区长度可靠性功能函数中采用的参数变量见表3。

采用交织区长度可靠度功能函数C,通过蒙特卡罗法计算其最小交织区长度的失效概率,式中LR=150 m,LS为的最小交织区长度计算如式(5),利用MATLAB进行计算,见表5。

表5 LR=150 m时交织区长度对应可靠度计算

在主线设计速度为100 km/h的条件下,通过分析及表3可知,若交织区长度采用的是现行规范的最小值即LR=150 m时,其可靠度指标β≈0.625 6;失效概率Pf≈26.65%;可靠概率Ps≈73.35%,因此《规范》中最小交织区长度可靠性在一定程度上没有符合安全等级为一级的可靠度要求(表4)。

同理,按照上述得分析步骤,亦可利用最小交织区长度可靠度功能函数计算出设计速度为80、60 km/h时现行规范中最小交织区长度的可靠度,结果如表6。

表6 可靠度功能函数计算结果

通过对表6数据的分析,在设计速度为100、80、60 km/h时,当采取现行规范中交织区长度的最小值LR=150 m时的失效概率Pf分别为26.65%、21.62%、15.64%,可靠概率Ps分别为73.35%、79.38%、84.36%,参考表4可知,采用该值作为最小交织区长度的安全可靠性在一定程度上没有满足安全等级为一级的安全可靠要求。因此,经笔者构建的交织区长度可靠度功能函数的检验,得出现行规范中所规定的交织区长度范围的最小值可靠概率较低,即安全可靠性较低。

3 基于可靠度的交织区长度

现行规范中规定新建城市快速路的设计应采用三级服务水平,可根据满足三级服务水平条件下,求出不同设计速度下交织区内总交通流量。由表4可知,城市快速路相对应的安全等级为一级,经过对已知相关参数变量的分析,反算笔者构建的交织区长度可靠度功能函数,从而得出所对应指标下道路所提供的交织区长度LR,所得对应数据见表7。

表7中的计算是在可靠概率95%的条件下进行反算,结果表明:当设计速度为100、80、60 km/h时,交织区长度的推荐值为400、370、350 m。

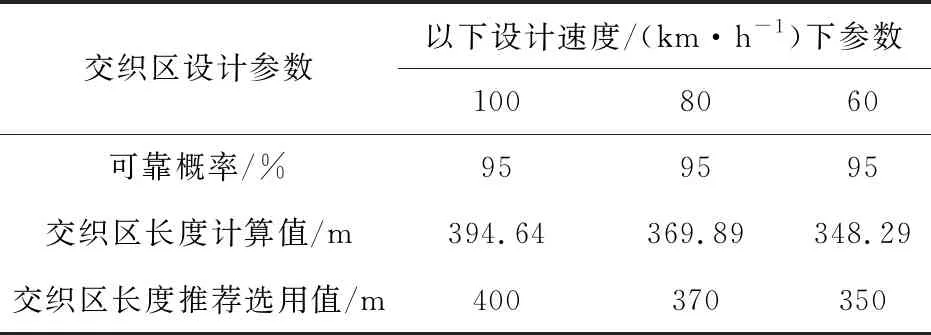
表7 交织区长度计算值及推荐选用值

4 实例分析

以某立交下游(由西向东方向)A型交织区为例,进行交织区长度可靠性分析,使用雷达枪,摄像机等仪器,通过录像并辅以人工调查获取交通流基础数据,其中主线车道数为双向四车道,设计速度为80 km/h;匝道车道数为单向一车道,设计速度为40 km/h,数据整理如表8。

表8 交织区交通流的基础数据

4.1 计算过程

基于实地所收集到的交通流数据,利用交织区长度对应的可靠度功能函数,进行MATLAB计算,从而得到其交织区长度的失效概率,并得到满足目标可靠度指标为1.64(即可靠概率为95%)所需的交织区长度。采用车流密度作为评价指标,将实例中所采用的交织区长度、满足目标可靠度指标为1.64所需的交织区长度以及表7中相对应的推荐交织区长度进行对比分析。计算结果见表9。

4.2 结果分析

1)经过对表9的结果进行分析可知,交织区长度为160 m时容易造成路段的拥堵,这与该路段高峰时期经常发生拥堵现象严重的事实相吻合。若采用交织区长度363.12 m,在一定程度上可以缓解交通拥堵严重这个问题。

2)通过对表9中95%交织区长度以及表7中交织区推荐值的对比,发现在安全等级为一级时,即可靠概率95%的条件下进行反算出的交织区长度,可以看出其较好地符合表7中基于可靠度理论的交织区长度推荐选用值。

5 结 语

根据我国《公路通行能力手册》中对交织区的相关理论知识,构建了城市快速路互通立交交织区长度计算模型,以该模型为基础并引入可靠度理论知识建立最小交织区长度可靠度功能函数,检验现行规范中交织区长度最小值的可靠性,发现其可靠概率较低不满足安全等级为一级的可靠性要求。根据在可靠概率95%的条件下即满足一级安全等级的前提下进行反算,求解得出不同设计速度下相应地基于可靠度理论知识的交织区长度推荐选用值。鉴于目前对城市快速路互通立交交织区长度没有明确的计算方法,在对以辅助车道相连的交织区长度设计时,为保证车辆完成车道变更行为所需要的距离且与城市快速路整体的道路通行能力相适应的要求,研究结论作为交织区长度设计取值的参考。