基于改进Logistic-SSA-BP神经网络的 地铁短时客流预测研究
2023-05-09胡明伟何国庆吴雯琳
胡明伟,何国庆,吴雯琳,赵 千
(1. 深圳大学 土木与交通工程学院,广东 深圳 518060; 2. 滨海城市韧性基础设施教育部重点实验室(深圳大学), 广东 深圳 518060; 3. 深圳大学 未来地下城市研究院,广东 深圳 518060)
0 引 言
城市地铁以其经济、便利、高效的运营优势,逐渐成为大众出行的首要选择,现在城市地铁的客流也与日俱增[1]。据相关统计,截至2021年6月全国41个城市地铁总客运量达19.61亿人次,日平均6 577.76万人次,比2019年6月上涨0.94%。面对日益庞大的地铁客流,通过历史客流数据精准预测未来的短时客流量,是地铁运营公司制定日常行车计划和突发事件紧急疏散预案的重要依据。因此,如何对城市地铁短时客流量进行高效、准确预测是地铁运营管理者所关注的问题。
近些年来,地铁客流短时预测领域的研究已受到国内外学者高度关注,常见的客流预测方法可分为统计学的客流预测方法和机器学习的客流预测方法。
统计学的客流预测方法包括平均模型、时间序列模型、指数平滑模型、卡尔曼滤波模型和非参数回归模型等[2-3]。B.M.WILLIAMS等[4]提出了基于季节性移动平均(SARIMA)的客流预测模型;韩超等[5]通过改进ARIMA,减少遗忘因子,以达到提升模型预测精度的目的;熊杰等[6]通过构建卡尔曼滤波模型,实时采集最新数据,以此得到早晚高峰期客流量的精准预测。
机器学习的客流预测方法主要包括支持向量机、贝叶斯及神经网络等[7]。HAN Huiting等[8]提出了基于XGBoost的高速铁路客流预测模型,通过对高铁订票信息作为重要的客流特征进行模型训练,得到的预测值比传统模型预测值精度更高;张淑玉等[9]从历史客流数据和预售期已售票额出发,提出了基于发车时间、行车时间、休息日等客流特征的贝叶斯预测模型,在客流预测中取得较好效果;李若怡等[10]将时空特征作为输入层,采用改进的LSTM模型对运营客流OD数据进行预测。
BP神经网络作为最典型的深度学习方法,被众多学者用于客流预测[11-12]。但传统BP神经网络常伴着准确度低、收敛时间长、结果易陷入局部最优等情况[13-17]。因此,学者们常通过其他算法对BP神经网络模型加以改进,从而提高预测结果的准确性和收敛速度。惠阳等[18]通过改进的粒子群算法,优化了BP神经网络,使地铁客流预测的准确性有极大提升;傅晨琳等[19]提出了基于集合经验模态分解法优化BP神经网络,构建了地铁客流短时预测模型,探究了日间客流波动的影响因素;张艺铭等[20]通过将余弦思想和动态权重改进的灰狼算法,与BP神经网络结合,达到提高轨道交通短时客流预测的目的;王国梁等[21]提出通过麻雀算法优化BP神经网络,建立了小米米粉糊化预测模型,由实验对比发现,优化后的BP神经网络能提高在小米米粉糊化特征指标回归、预测上的优势。
麻雀搜索算法(sparrow search algorithm, SSA)[22-25]是近年来提出的一种新型启发式算法,它来源于麻雀的捕食和反捕食行为,具有寻优能力强、收敛速度快、全局性良好等特点;在故障检验、关键参数辨识、路径优化等方面有着较好的效果,但在地铁客流预测上的研究较少。鉴于此,笔者提出了一种新的BP神经网络回归预测模型(Logistic-SSA-BP)。该模型利用Logistic混沌映射后的麻雀搜索算法(Logistic-SSA)寻优能力强、收敛速度快的特点,对传统的BP神经网络进行改进,提升了其在地铁客流预测中的收敛速度和预测精度,并通过深圳地铁历史客流数据进行了实例验证。
1 SSA与BP神经网络原理
1.1 SSA原理
SSA算法是根据麻雀捕食与躲避捕食行为提出的新型启发式优化算法。相较于其他传统算法,该算法在精度、收敛速度和稳定性上都具有一定优势[26]。SSA算法建模过程如图1。

图1 麻雀算法(SSA)流程
其具体步骤如下:
步骤1:确定初始化种群;
步骤2:确定种群迭代次数,以及初始探索者和融入者比例;
步骤3:计算族群适应度值;
步骤4:通过式(1)迭代探索者位置;
步骤5:通过式(2)迭代融入者位置;
步骤6:通过式(3)迭代预警者位置;
步骤7:计算适应度值和麻雀位置;
步骤8:判断是否符合终止条件,若符合则退出计算,并输出最终结果,否则,回到步骤2重新开始计算。
麻雀群作为一个智能群体,在捕食过程中具有明显的分工行为,分别为探索者、融入者和预警者。其中:探索者作为主要的食物搜索个体,往往最快找到食物,融入者是一部分跟随探索者的个体,预警者是麻雀群中负责预警的个体,当危险来临时,会提醒放弃捕食行为。通常由于探索者负责发现食物,所以具有最大的搜索区域[27],在模型中表现为较高的适应度值。探索者和融入者身份是随时动态变化的,当预警值大于安全阀值时,探索者会将融入者带到其它安全地区进行捕食。
SSA算法中经过每次迭代,探索者的位置更新为如式(1):
(1)
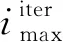
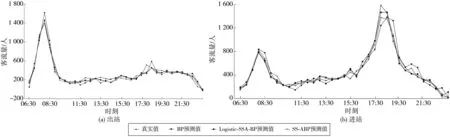
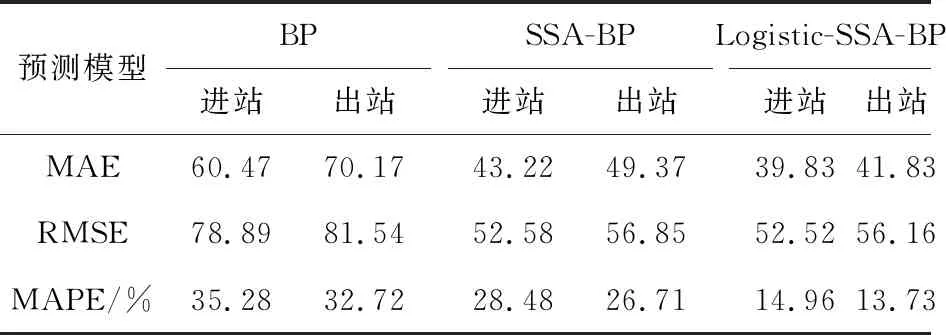
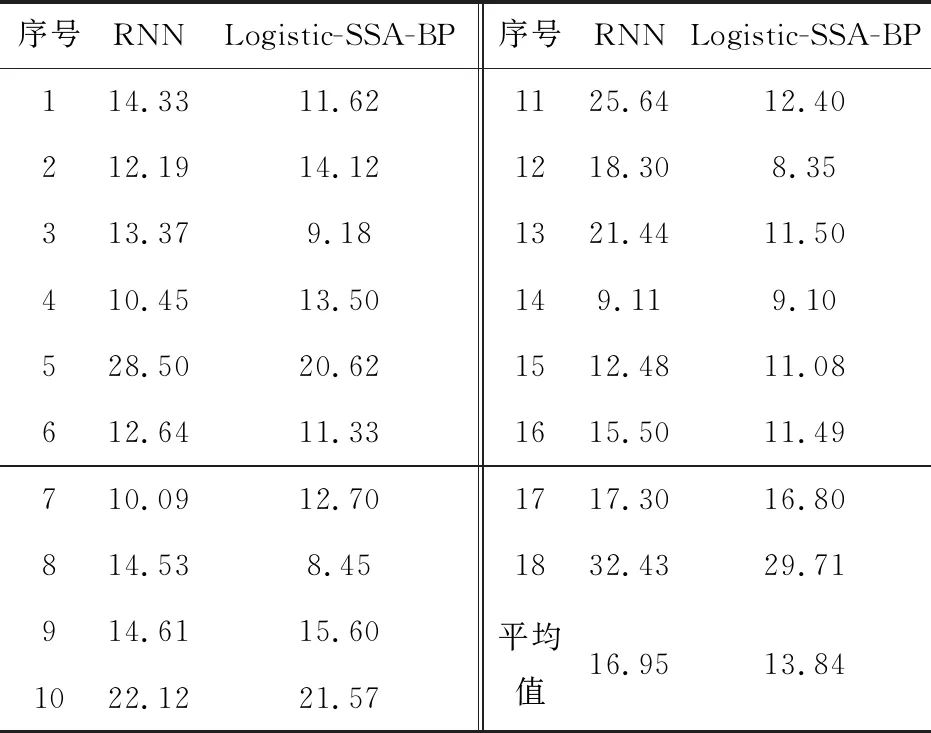
若R2≥SST时,意味着族群中一部分麻雀发现危险,并向族群发出预警信息,此时整个种群中的麻雀会立即飞往其它安全地区捕食;若R2 融入者在跟随探索者过程中,其位置更新如式(2): (2) 式中:A为l×d的矩阵,矩阵中每个元素取值为1或-1,且A+=AT(AAT)-1;n为族群规模;XP为当前探索者位置;Xworst为当前所有捕食的最差位置。 若i>n/2时,表示第i个融入者的适应度值较低,必须到其他区域捕食,以此获得更多能量。 预警者作为族群中最先发现危险的麻雀,初始位置会在族群中随机生成,其表达如式(3): (3) 若fi>fg时,说明麻雀正位于族群边缘,可能会出现被捕食的危险;若fi=fg时,说明麻雀察觉到危险,为躲避危险,会尽可能向其它麻雀靠拢。 BP(back propagation)神经网络实质是多层感知器的一种,它能按误差逆传播进行算法训练,是应用最为普遍、最为成功的神经网络模型之一[28-29]。BP神经网络模型结构由3部分组成,分别为输入层(input)、隐藏层(hide layer)和输出层(output layer),每部分可由多个神经元组成,常见的BP神经网络中隐藏层可有单层和多层之分,其结构如图2。 图2 BP神经网络结构 对于绝大部分预测模拟实验而言,单层隐藏层具有精度高且速度快的优势[30]。通常决定BP神经网络性能高低的参数主要取决于隐藏层节点数、激活函数和学习效率的选取。隐藏层神经元个数越少,BP神经网络模拟效果就越差,反之隐藏层神经元个数越多,BP神经网络模拟效果越好;激活函数和学习率的选取决定了识别率和收敛速度,若设定的学习率过低,会造成神经网络的收敛时间变长,相反若设定的学习率过高,则可能导致模拟无法收敛,甚至还会降低识别率。 为避免麻雀搜索算法(SSA)因收敛变化使族群多样性下降,陷入局部最优问题,笔者采用Logistic混沌映射初始化麻雀族群,对族群中的适应度进行排序,取靠前个体作为初始化族群,以此在一定程度上增加族群多样性,提高输出结果精确度。Logistic混沌映射作为经典的混沌映射方法之一,被广泛的应用于安全、通信领域。其表达如式(4): Xn+1=α×Xn× (1-Xn) (4) 式中:α∈[0, 4],Xn∈[0, 1]。 当0≤Xn≤1时,初始条件X0在Logistic映射下其序列呈现非周期、不收敛状态,而此范围之外,产生的序列必定收敛于特定值。 笔者采用Logistic混沌映射方法优化麻雀搜索算法(SSA),提高初始麻雀族群质量,有助于增强算法收敛性和精确性,然后将改进后的算法用于优化BP神经网络,并结合训练集和测试集数据样本,设计改进麻雀算法的适应度函数EFitness,其模型如式(5): (5) 式中:TTrain为训练集的样本;TTest为测试集的样本。 根据适应度函数值的大小,能直观反应训练和预测的准确性,若计算得到的适应度函数值越小,即均方误差EMS越小,表示训练越准确,且模型的预测精度更好。 笔者构建了Logistic-SSA-BP神经网络预测模型,借助Logistic-SSA算法的优秀寻优能力和迅捷收敛优势,能提升预测结果的精度。其建模过程如图3。 图3 Logistic-SSA-BP预测模型流程 具体步骤如下: 步骤1:初始化参数; 步骤2:确定BP神经网络的拓扑结构; 步骤3:通过Logistic混沌映射法对族群进行初始化处理,调整族群规模、迭代次数、探索者、融入者和预警者比例; 步骤4:计算族群中适应度值,并对不同的适应度值进行排序,得到最优适应度fg和最差适应度fw; 步骤5:通过式(1)~式(3),更新探索者、融入者、预警者位置信息; 步骤6:判断位置信息是否满足终止条件,若满足,则输出最优位置信息,进入步骤7,若不满足,则回到步骤3,直至位置信息满足终止条件(是否达到最大迭代次数或达到最初设定的收敛精度); 步骤7:根据最优位置信息,输出BP神经网络最优权值和阀值参数; 步骤8:对数据训练集进行神经网络训练; 步骤9:测试集进行仿真预测,输出预测结果。 在深度学习领域中,预测模型的准确性评价是一个不可或缺的环节,不同类型的模型评价方法也大相径庭。为反映真实值和预测值误差的同时,还能进一步计算误差占真实值的百分比,因此笔者以平均绝对误差、均方根误差及平均绝对百分误差作为客流预测模型准确性的评价指标。 在真实值和预测值差值的绝对值基础上,通过求解算术平均值的方式来避免误差抵消问题。平均绝对误差(MAE)指标值大小(用EMA表示)直接反映模型性能的好坏,若值越小则性能越好,若越大,则相反。其具体表达如式(6): (6) 对于某些误差值比较敏感,能够明显反映预测值与真实值的偏离程度。若均方根误差值(用ERMS表示)越小,则反映预测值与真实值越接近,对应的预测模型性能越好;若均方根误差值越大,则表明预测模型性能越差。其具体表达如式(7): (7) 在反映预测模型真实值和预测值之间误差的同时,还反映误差与真实值的百分比。若平均绝对百分误差值(用EMPA表示)越小,则表明模型预测值越接近真实值,模型性能越好,预测精度越高,若平均绝对百分误差越大,则相反。其具体表达如式(8): (8) 在式(6)—式(8)中:xi表示真实值;x′i表示预测值;N代表样本个数。 为检验文中所提出的Logistic-SSA-BP回归预测模型是否有效。笔者选择深圳地铁一号线西乡站2017年9月1日—9月30日早上06:30—23:30的AFC进、出站刷卡数据作为实验原始数据,原始数据以30 min为粒度进行统计,数据量共2 040组。其中:实验以9月份前29 d进、出站刷卡数据为训练样本,第30 d进、出站数据为测试样本,将得到的预测值分别与真实值进行对比(用于检验真实值与不同模型预测值情况)。 根据对3种模型(BP、SSA-BP、Logistic-SSA-BP)预测流程的分析,为方便对比不同种类神经网络预测模型的预测精度及收敛速度,实验中所有神经网络预测模型均采用部分相同参数的设置。例如:模型训练次数统一设为1 000次,模型学习速度为0.01,训练目标最小误差为0.000 01,最大迭代次数为100。具体参数设置如表1。 表1 3种预测模型参数设置 实验采用MATLAB 2016a软件对原始数据进行编程处理,处理过程包括错误与冗余数据修改,划分训练集与测试集,对数据进行归一化处理等。将处理完毕的数据分别输入到文中构建的BP、SSA-BP、Logistic-SSA-BP神经网络预测模型中,进行地铁短时客流预测,最终实验预测结果,如图4、图5。图4为测试数据集的真实值与不同模型短时预测值对比情况;图5为Logistic-SSA-BP与SSA-BP适应度曲线情况。 由图4可知:深圳市西乡站全天进、出站客流存在明显的早晚高峰潮汐现象,早高峰一般集中在07:30—08:30,晚高峰一般集中在18:00—19:00。图4中:无论是传统BP神经网络预测模型,还是改进过的SSA-BP及Logistic-SSA-BP模型,都可以捕捉到西乡站进、出站客流早晚高峰的客流特征,对客流的变化态势以及峰值拟合都较为准确,可以实现较好的客流预测效果。 由图5可知:经Logistic混沌映射的麻雀搜索算法优化BP神经网络,其预测速度及适应度值下降速度明显加快、种群进化代数明显更少,反映出改进后的模型其预测效率更高。 图4 不同模型预测结果与真实值对比 图5 Logistic-SSA-BP与SSA-BP的适应度曲线 为更明显评判3种BP神经网络模型的预测结果,笔者根据式(6)~式(8)分别计算3种预测模型的MAE、RMSE和MAPE,并通过计算值进行横向对比分析。具体指标对比情况如表2。 表2 3种预测模型的评价指标对比 由表2可知:不同模型的评价指标值存在明显差异,改进后的BP模型要比传统BP神经网络预测模型效果更好。Logistic-SSA-BP模型的进站客流预测,EMA=39.83,ERMS=52.52,EMAP=14.96%;出站客流预测,EMA=41.83,ERMS=56.16,EMAP=13.73%。与传统BP预测模型相比,Logistic-SSA-BP进站客流预测结果的EMA下降了20.64,ERMS下降了26.37,EMAP下降了20.32%;出站客流预测的EMA下降了28.34,ERMS下降了25.38,EMAP下降了18.99%。这表明:Logistic-SSA-BP比传统BP模型预测值更加接近真实值,模型精度越高、性能也越好。 为更好的验证文中提出的Logistic-SSA-BP模型在地铁客流预测方面的优越性和稳定性,利用RNN神经网络对地铁客流进行预测,并将预测结果与文中模型进行对比。为保证结果可比性,在RNN神经网络预测中,同样选取数据集前29 d数据为训练集,最后一天数据(以1 h为时间间隔)为测试集。两者的相对误差如表3。 表3 RNN与Logistic-SSA-BP预测结果相对误差及平均值 从表3可看出:RNN预测结果与真实值的相对误差为9.11%~33.43%;Logistic-SSA-BP的相对误差为8.35%~29.71%。Logistic-SSA-BP的相对误差平均值比RNN小3.11%,由此说明在客流预测的优越性和稳定性上Logistic-SSA-BP模型效果更好。 综上,通过Logistic-SSA优化BP神经网络,并将其用于地铁客流预测是可行的,与其他算法相比,具有更好的效果。 地铁短时客流预测对提高城市轨道交通系统的运行效率,优化运营组织结构,为乘客提供更加安全、优质的出行服务具有重要意义。笔者鉴于传统BP神经网络模型在预测客流时表现出的准确度低、收敛速度慢、易陷入局部最优值的问题,利用麻雀搜索算法(SSA)对BP神经网络的权值和阀值进行优化,以此提高客流预测精确度和准确性。同时考虑到SSA算法全局搜索能力较弱的缺点,利用Logistic混沌映射对SSA算法种群进行初始化,以此提高算法全局搜索能力和稳定性,最终得到了改进后的BP神经网络回归预测模型(Logistic-SSA-BP)。 通过比较基于MAE、RMSE和MAPE这3种评价指标的模型预测结果可发现:与传统BP神经网络预测模型相比,进出站的EMA平均减少24.49,ERMS平均减少25.88,EMAP平均减少19.66%;此外通过与RNN预测模型对比,相对误差范围和平均值更小。由此表明基于Logistic-SSA算法优化后的BP神经网络预测模型在短时客流预测方面效果更好,准确度更高。 笔者利用改进后的SSA算法优化了BP神经网络模型,并将其应用于城市轨道交通短时客流预测研究中;通过深圳市西乡地铁站的进、出站客流数据进行了实例验证。
1.2 BP神经网络原理
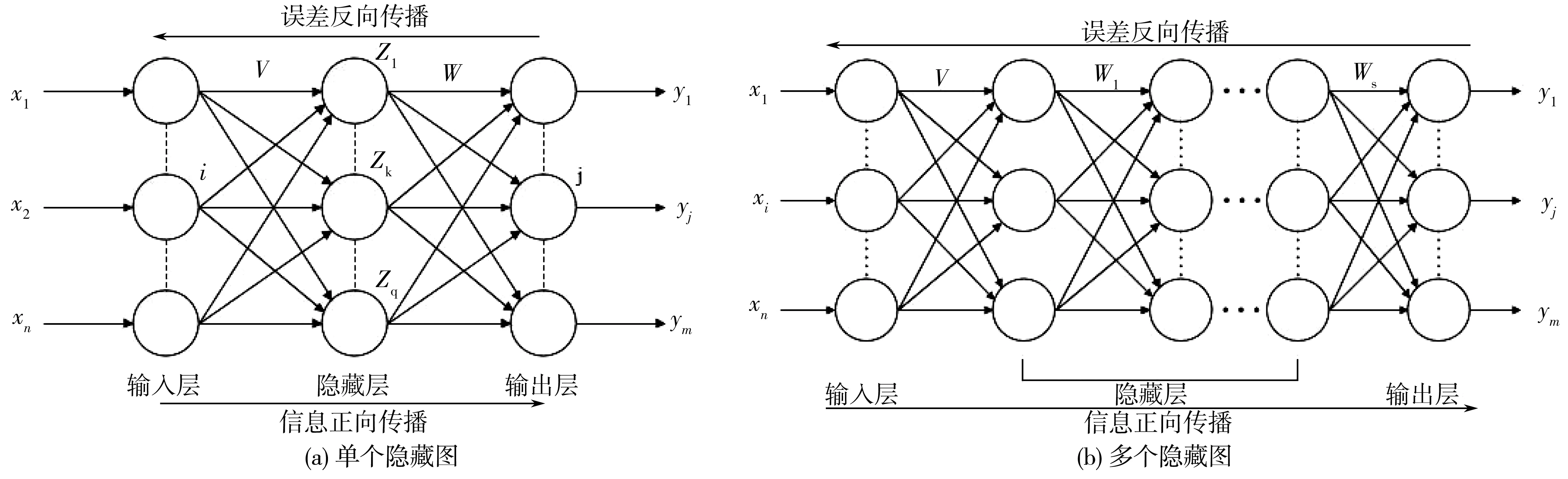
2 改进的Logistic-SSA-BP预测模型
2.1 Logistic混沌映射优化
2.2 Logistic-SSA-BP模型

3 模型准确性评价指标
3.1 平均绝对误差(MAE)
3.2 均方根误差(RMSE)
3.3 平均绝对百分误差(MAPE)
4 实例分析
4.1 样本数据来源
4.2 模型参数设置

4.3 预测结果分析

5 结 论
