基于四维广义离散椭球序列的降秩MIMO-OFDM信道估计方法

王妍

(中铁第一勘察设计院集团有限公司,陕西 西安 710043)

近年来,随着高铁的快速发展,无线通信技术受到广泛关注,高铁通信系统在列车运行安全以及宽带通信服务等方面发挥着重要作用[1]。目前,高铁通信技术发展面临的主要问题是快速时变和非平稳的传播信道,再加上高铁运行环境中存在视距(LOS)分量与散射体,这导致其与广义平稳非相关散射(WSSUS)条件相违背。因此,可靠的高铁无线通信需要稳健的信道估计和均衡。

导频辅助的正交频分复用(OFDM)信道估计方法有三种,即基于插值的方法、参数模型(PM)方法和基扩展模型方法。传统的基于插值的方法通过在导频处使用估计的信道频率响应的多维插值来重建数据位置处的信道。刘俊琳等[2],Uwaechia等[3]分别采用二维和三维插值对单输入单输出(SISO)和多输入多输出(MIMO) OFDM信道进行了估计。PM信道估计方法使用导频符号直接估计多径信道参数,例如路径数、路径增益、延迟、到达角(AOA)和离开角(AOD)。与基于插值的估计器相比,PM信道估计器具有更好的性能,因为稀疏的多径信道建模只需要少量参数[4]。然而,对于快速时变的频选信道,基于插值和PM的方法均需高导频开销来跟踪各OFDM模块内的信道系数或多径参数的时间变化。考虑到双选信道仅限于低维子空间,一些文献建议使用基扩展模型来进一步减小信道维度,从而减小用于快速时变信道的导频开销。Talaei等[5]基于离散椭球序列为各子载波设计了降阶信道估计器;陈发堂等[6]通过信道协方差矩阵的奇异值分解设计了基于子载波之间频域相关性的低维信道估计器;Rossi等[7],Karnik等[8]在时间和频率上使用了信道的连续Slepian子空间投影,将各天线对视为一个SISO-OFDM信道,通过对SISO-OFDM信道逐一估计即可得到不同天线的信道。对于高铁通信系统的MIMO-OFDM信道估计,现有的研究均未考虑额外的空间域相关性以及时间和频率的相关性,这样就很难获得准确的信道估计和更低的导频开销。本文基于四维基扩展通道模型设计了一种降秩线性最小均方误差(LMMSE)信道估计器,并基于规则形状的几何随机模型(RS-GBSM)对所设计的时变信道估计器的有效性进行了验证。

1 系统模型

假设高铁MIMO-OFDM系统中,各OFDM符号包含N个子载波和MTx个空间数据流,这些空间数据流对应有MTx个发射天线和MRx个接收天线。各发射天线的传输是基于帧长的M个OFDM符号。系统带宽为B且OFDM符号的持续时间Ts=(N+G)Tc,其中G为循环前缀长度且Tc=1/B。在第m个OFDM符号、第q个子载波和第s个发射天线的发射符号定义为

(1)

式中:b(m,q,s)和p(m,q,s)分别为QPSK调制数据和导频符号;m为以采样周期为单位的时间索引;Sd表示整数数据位置的集合,Sd∈Z3;Sp表示整数导频位置的集合,Sp∈Z3。

第r个接收天线上的信号y(m,q,r)是在时间m时,子载波q从MTx个发射天线发送的MTx个数据符号的叠加,即

(2)

式中:h(m,q,r,s)为采样的信道频率响应;z(m,q,r)为复数高斯白噪声分量。

2 基于几何随机模型(GBSM)的宽带MIMO高铁信道

为了对信道进行建模,本文使用多抽头RS-GBSM(针对高铁通信中非平稳宽带MIMO信道提出的[9])。在该模型中,假设散射体分布在NT个共焦椭圆上(NT个抽头),基站和接收器天线阵列位于焦点处。在第i个椭圆上有Ni个有效散射体,其AOD扩展和AOA扩展随时间变化。考虑到环境中存在漫散射体,因此通道由LOS分量和非LOS (NLOS)分量组成。通过时变传递函数来描述信道

式中:t、f、y和x分别表示时间、频率、接收天线和发射天线在其各自阵列上的位置。用Δf=1/(NTc)表示频率区间宽度,而Δx和Δy分别表示发射和接收天线阵列中相邻天线之间的距离。采样的NLOS信道传递函数是多径分量的叠加,即

(3)

(4)

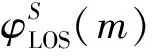
3 广义离散椭球(GDPS)信道模型

本文通过低维子空间在时域、频域和空间域中表示高铁的MIMO-OFDM信道,并为此信道模型设计LMMSE估计器。为了得到降秩LMMSE,协方差矩阵的特征向量被认为是跨越低维子空间的最优基[6]。本节将通过GDPS序列跨越的四维子空间模型来近似信道协方差矩阵的时变特征向量。

3.1 GDPS序列

(5)

D′(W,M)=「|W|M⎤+1

(6)

3.2 四维GDPS信道模型

本节基于信道在不同域的带宽限制,对高铁MIMO-OFDM信道使用四维基扩展模型,h(m,q,r,s)的最大带宽限制为

Wmax=Wt×Wf×Wx×Wy

(7)

式中:Wt=[-υmax;υmax];Wf=[0,θmax]。Wx=[ζmin,ζmax]和Wy=[ξmin,ξmax]分别是信道在时间、频率、发射天线空间域和接收天线空间域的最大支撑。θmax=τmaxΔf表示信道的最大归一化延迟,ζmin,ζmax,ξmin和ξmax分别为

(8)

其中,最大化、最小化在所有散射体之间及整个框架之上。高铁MIMO-OFDM信道的频带限制特性允许通过以下四维子空间模型表示M个OFDM符号帧上所有天线的信道。

(9)

式中:

分别跨在时间域、频率域、接收天线空间域和发射天线空间域等各子空间;ψdt,df,dy,dx是相应的GDPS基的权重系数;Dt,Df,Dy,Dx是子空间的维数,对于高铁通信系统,υmax≪1意味着|Wt|≪1,因此,Dt≪M。类似地,最大超额延迟在通信系统中受到限制,由此导致|Wf|≪1且Df≪N。考虑到具有有限AOD和AOA扩展的非各向同性散射以及发射和接收天线阵列中天线之间的适当距离,可得Dx≪MTx且Dy≪MRx。

4 信道估计

4.1 问题描述

考虑到式(9)中提出的信道模型,可将式(2)重新表述为

(10)

根据式(10),信道估计问题可简化为基的权值系数的估计。为了得到ψdt,df,dy,dx,可将式(10)改写为矩阵-向量形式,按照以下顺序收集向量Ψ中的所有基的权值系数

Ψ(dtDfDyDx+dfDyDx+dyDx+dx+1)=

ψdt,df,dy,dx

(11)

类似地,定义包含接收数据值y(m,q,r)和相应噪声值z(m,q,r)的矢量y和z为

y(mNMRx+qMRx+r+1)=y(m,q,r)

z(mNMRx+qMRx+r+1)=z(m,q,r)

(12)

由式(11)和式(12)可知最终的输入输出关系为

y=DΨ+z

(13)

式中:D为mNMRx×DtDfDyDx矩阵,其行向量可以表示为

D(mNMRx+qMRx+r,:)=

(14)

式中:

(15)

D1仅取决于GDPS的基;fd取决于导频数据。

4.2 基扩展系数的LMMSE估计

式(13)中基的权系数向量的线性估计可表示为

(16)

计算协方差矩阵,式(16)可简化为

(17)

(18)

(19)

式中:im,q,ri=mNMRx+qMRx+ri,i=1, 2;r1,r2∈{1,…,MRx}。此外,对于所提出的四维GDPS信道模型,协方差矩阵CΨ由式(20)给出

(20)

5 仿真结果

取M=14,N=128,MTx=MRx=4,fc=1.8 GHz,Ts=8 μs,B=1/Tc=20 MHz,RS-GBSM的信道参数见表1。因为|Wt|=2υmax=2vRfcTs/c,最大归一化多普勒扩展由高铁速度vR控制,考虑到相邻信道抽头间的距离为Tc, 最大归一化延迟扩展为

|Wf|=θmax=NT/N。

表1 RS-GBSM的信道参数

高架桥与路堑场景是两种最主要的高铁通信环境,文献[10]的测量结果表明,路堑比高架桥场景的通信环境更为恶劣。因此,本文选择路堑场景进行仿真,其两个斜坡表面上散射体的复路径幅度可表示为

(21)

式中:ci是第i个散射体的零均值复高斯增益;nDI=3,G0,DI=23 dB是路径损耗指数和参考功率;dT→i和di→R分别是散射体到基站和高铁的距离。路堑场景中的Rician-K因子遵循对数正态分布,均值为0.94 dB,标准差为4.18 dB。

就归一化均方误差(NMSE)而言,本文所设计的基于GDPS的信道估计器性能优于传统的基于插值的LS方案(图1),然而,MMSE信道估计器优于本设计方案,因为MMSE方法使用完整的信道相关信息进行了导频子载波上的信道估计和数据子载波上的插值。

图1 导频开销为0.013 5的不同估计器性能比较

不同AOD和AOA扩展的信道估计器性能见图2。对所有情况,取Dt=2,Df=11,Dx=2,由此产生的导频开销均为0.013 5。由于相同数量的基被用于跨越发射天线空间域,因此,对于更大的AOD扩展,性能有所下降。此外,对于更大的AOA扩展,更多的GDPS基可用于信道建模,从而提高估计精度。同时,本文对不同情况下Dy的平均值进行了计算。

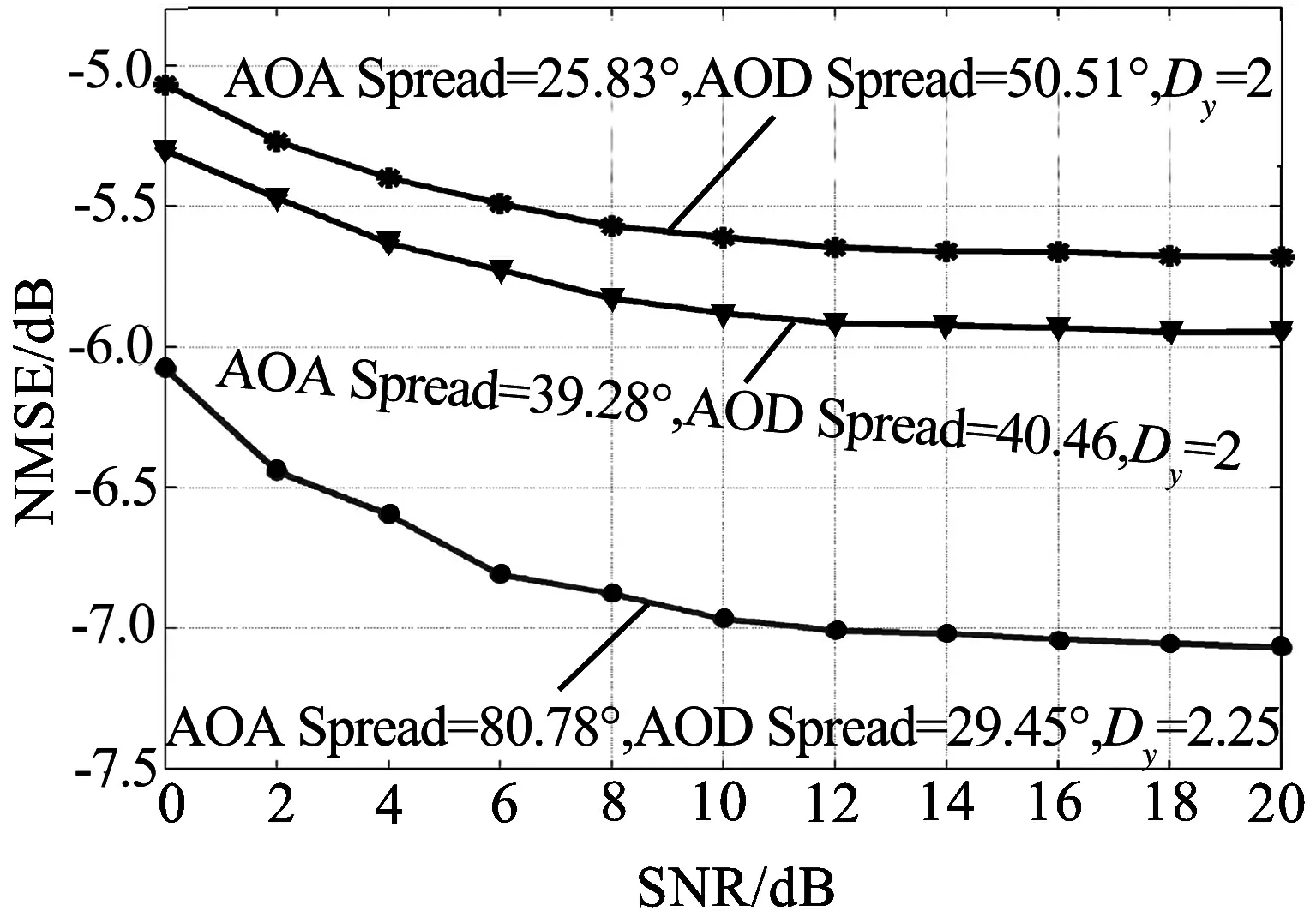
图2 不同AOD/AOA扩展下的信道估计器性能

图3揭示了不同天线尺寸对信道估计器性能的影响。对于具有相同导频开销的天线,增大天线尺寸将增加用于信道建模的基数量,由此可以提供更好的信道近似。然而,对于发射天线阵列,增大天线尺寸会降低性能,因为发射天线空间域中的导频开销对于所有天线尺寸都是相同的。对于接收天线空间域,由于在所有接收天线处都要对信道进行采样,因此有足够样本来估计增加的基的权值系数数量。因此,更大的接收天线阵列尺寸能得到更好的信道估计器性能。

图3 不同天线尺寸下的信道估计器性能

图4揭示了不同延迟扩展对信道估计精度的影响。对于不同数量的频域基,各应用场景都有不同的导频开销。由于导频开销会根据不同情况进行调整,因此,不同情况下NMSE的差异不会很大。

图4 不同时延扩展下的信道估计器性能

图5揭示了不同高铁速度下所设计信道估计器的性能。显然,对于相同的导频开销,高铁速度越大,信道估计器性能越差。

图5 不同高铁速度下的信道估计器性能

(22)

计算复杂度可通过式(23)计算

(23)

例如,对于8×8的MIMO,根据表1中的参数可得Dt=2,Df=11,Dy=3,Dx=3,降低的相对复杂度Cfull/CGDPS=1.224 6×106。

6 结论

考虑到高铁MIMO-OFDM信道在时间、频率和空间上的相关性,本文提出了一种基于四维GDPS信道模型的降秩LMMSE估计器。对于相同的导频开销和较低的计算复杂度,与传统的基于插值的LS和MMSE信道估计器相比,基于GDPS的信道估计器性能良好。高铁路堑场景和非平稳RS-GBSM信道模型的仿真结果证明了所设计信道估计器对不同天线尺寸和不同高铁速度、延迟和角扩展均具有良好的稳健性能。