基于一种贝叶斯优化框架的高空螺旋桨气动优化设计
2023-05-09口启慧王海峰刘坤澎职鑫鑫
口启慧,王海峰,刘坤澎,职鑫鑫
(西北工业大学 航空学院,西安 710072)
0 引 言
高空长航时飞行平台通常指运行在平流层、能长时间工作的飞行器,如平流层飞艇、高空太阳能无人机等。高空长航时飞行平台的特点使其在通信、对地观测等领域有着广泛的应用前景。由电机驱动的螺旋桨推进系统是高空长航时飞行平台的主要动力[1],其中螺旋桨的推进效率对整个推进系统的效率影响重大,进而影响飞行平台的续航能力。高空空气密度和黏度与地面值差异较大,且通常要求螺旋桨桨尖马赫数小于1以避免跨声速带来的激波问题。因此高空螺旋桨的桨尖雷诺数通常低于1 × 106,其气动问题是一个低雷诺数问题。在飞行平台功率和桨叶直径的限制下,获得高效的高空螺旋桨气动优化方案是需要解决的关键设计问题。
针对以上问题,各国学者对高空螺旋桨气动优化设计进行了研究。Zhang等用不同优化方法设计低雷诺数翼型[2]。Morgado等使用JBLADE软件进行高空螺旋桨设计优化[3]。Mourousias等对高空螺旋桨进行基于叶素动量理论和Kriging代理的多点多目标优化[4]。García-Gutiérrez 等发展了一种基于非侵入式多项式混沌展开的螺旋桨设计算法,以平流层飞艇螺旋桨为例进行验证[5-6]。Ma等耦合直接优化算法EXTREM和XFOIL,为低速低雷诺数翼型的多点设计问题提供有效解决方案[7]。Jiao等提出平流层飞艇螺旋桨的多目标优化和验证方法[8]。Duan、Liu、Park等分别基于叶素动量理论和涡流理论提出高空螺旋桨设计优化方法,对设计结果进行计算和试验验证[9-11]。从文献中可以看出,目前高空螺旋桨的优化设计大多都基于叶素/涡流理论。这种计算方法的优点是有较快的气动性能计算速度,但其计算精度较低、寻找理论最优解较为困难。CFD数值模拟虽然具有较高的计算精度,但优化设计中使用其获得气动性能造成的时间成本难以接受。
贝叶斯优化(Bayesian optimization, BO)是一种数据驱动进化优化算法,具有很强的自适应和自学习特征[12]。该算法以可变精度的高斯过程模型代替获取耗时的真实目标函数,通过历史数据和采样函数,进行样本点更新,逼近局部或全局最优解,并保证所产生的样本点精确收敛于优化问题的真实最优解。对于复杂多维问题,其代替模型不必在整个设计空间内具有高的近似精度,而只需在关键区域,特别是最优解附近,具有高的近似精度。贝叶斯优化已逐渐被应用于气动优化设计领域[13-16]。
本文提出了一种基于贝叶斯优化框架的高空螺旋桨气动优化设计方法,通过试验验证了框架中使用的数值模拟方法的准确性,并使用该方法对某高空太阳能无人机螺旋桨进行优化设计。
1 螺旋桨参数化方法
1.1 低雷诺数翼型
翼型是螺旋桨设计的基础。传统翼型在高空、低雷诺数环境下,随迎角增加,升力系数增加缓慢,阻力系数增加迅速,翼型升阻特性显著下降。本文暂不考虑翼型的优化设计过程,直接使用课题组研发的PLRY系列翼型(共6个)。图1给出了其中部分翼型典型径向剖面的几何形状。
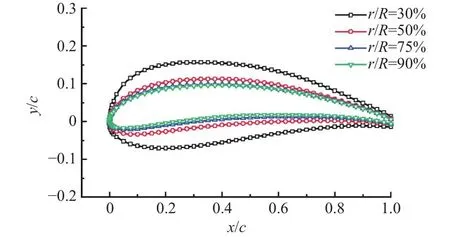
图1 部分翼型典型径向剖面示意图Fig.1 Airfoil radial profiles
高空螺旋桨从根部到尖部涵盖低速、亚声速或高亚声速范畴,采用系列翼型可以综合兼顾高升力和高升阻比,具有几何兼容和气动兼容等特点。该系列翼型相对厚度由桨根向桨尖逐渐减小,根部厚、尖部薄的特点也为提高螺旋桨结构刚度提供了条件。
1.2 螺旋桨几何参数化
螺旋桨由外形完全相同的桨叶组成,因此螺旋桨的设计需要先进行桨叶几何外形设计,再以此为基础计算螺旋桨气动性能。目前桨叶的设计不是直接进行几何坐标设计,而是将桨叶划分为多个剖面,选定一个或一组翼型作为各剖面基本翼型,保持桨叶各剖面翼型不变,通过设计各剖面翼型的实际弦长和扭转角确定桨叶的几何外形,然后通过螺旋桨气动性能(推力、效率、功率等)判定设计方案的优劣。
基于桨叶弦长和扭角分布特点,本文使用二次函数参数化方法来描述桨叶弦长和扭转角分布,保证了桨叶气动外形沿展向光滑连续。同时,与直接使用弦长和扭转角作为设计变量相比,该方法减少了变量个数,降低了设计空间维数,设计变量个数不会随剖面数量而变化,提高了螺旋桨优化收敛速度。
高空螺旋的每片桨叶从根部到尖部可以分为内段、中段和外段,其中中段和外段贡献了其整体推力的80%~90%[17]。本文定义螺旋桨相对半径r/R= 0.2(R为螺旋桨半径)所在的剖面为内段和中段分界面。根据PLRY系列翼型特点,其有效气动外形被划分为12个截面。从根部开始,1~3剖面翼型相同,4~6剖面使用3个不同翼型,7~9剖面翼型相同,10~12剖面翼型相同。
1.2.1 弦长参数化
弦长参数化方法如式(1)所示,弦长最大点将该函数分为两个二次函数。该函数在分段点(弦长最大位置)处连续可导,保证了弦长在最大位置处的光滑。
其中:x为剖面位置;xmax为最大弦长所在剖面位置;xtip为桨尖位置(等于螺旋桨半径);c为剖面弦长;cmax为最大剖面弦长;croot为根部弦长;ctip为桨尖弦长。上述变量单位均为mm。桨叶弦长的参数化变量共 5 个:croot、xmax、cmax、xtip、ctip。
1.2.2 扭转角参数化
扭转角参数化方法如式(2):
其中:x为剖面位置,单位为mm;xp为分布函数极值点位置,单位为 mm;β为剖面扭转角,单位为 (°);βroot为根部扭转角,单位为 (°);βtip为桨尖扭转角,单位为 (°)。桨叶扭转角的参数化变量共 3 个:βroot、βtip、xp。
通过以上选取的系列翼型及螺旋桨几何参数,即可确定各剖面弦长和扭转角。带弦长和扭转角的各翼型前后缘坐标可生成三条三次样条曲线(前缘一条,后缘两条),样条曲线和各剖面翼型共同构成桨叶气动外形轮廓。以桨叶轮廓为基础,使用光滑曲面可生成其气动外形。
2 数值模拟
2.1 模拟方法
采用非结构化网格进行数值模拟,采用网格自动化技术完成适应桨叶外形变化的流场网格和贴体网格划分,在桨尖和前后缘进行局部网格加密,网格数量大约1 200万,其中内场网格数量大约900万,外场网格大约300万。共15层附面层网格,第一层附面层网格高度为0.002 mm(y+<1)。流场尺寸如图2所示。使用滑移网格方法,其中内场为旋转域,外场为静止域。数值模拟采用基于有限体积法(finite volume method, FVM)的CFX完成,湍流模型使用SSTk-ω二方程模型,对流项离散格式为二阶迎风。仿真条件如表1所示。数值模拟收敛准则采用均方根(root mean square, RMS)残差类型,残差精度为 1 × 10-4。
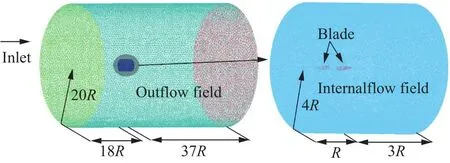
图2 CFD模拟流场尺寸示意图Fig.2 Sketch of CFD simulation domain

表1 CFD求解器设置Table 1 CFD solver settings
2.2 模拟方法验证
为验证数值模拟方法的准确性,使用该方法对某高空螺旋桨的地面气动性能进行数值模拟,并与试验测试结果进行对比。模拟条件与试验的工况参数相同(见表2)。

表2 设计工况Table 2 Design condition
螺旋桨地面静推力试验在西北工业大学的试验台进行(图3)。试验现场环境温度34.54℃,相对湿度60.2%。试验考虑了环境对结果的影响,共进行了三次测试。图4给出了测试数据和仿真数据对比。从图中可以看出,三次试验结果基本一致,验证了测试系统的稳定性。试验数据与仿真数据变化趋势一致。相同转速下,推力平均误差约2.34%,最大误差约5.66%;最大推力误差发生在第一次试验转速为175 r/min时,其余两次试验在该转速时的推力误差分别为1.74%和2.41%。扭矩平均误差约3.33%,最大误差约6.79%;最大扭矩误差发生在第一次试验转速为75 r/min时,其余两次试验在该转速时的扭矩误差分别为2.89%和3.35%。

图3 地面静推力测试Fig.3 Ground thrust test
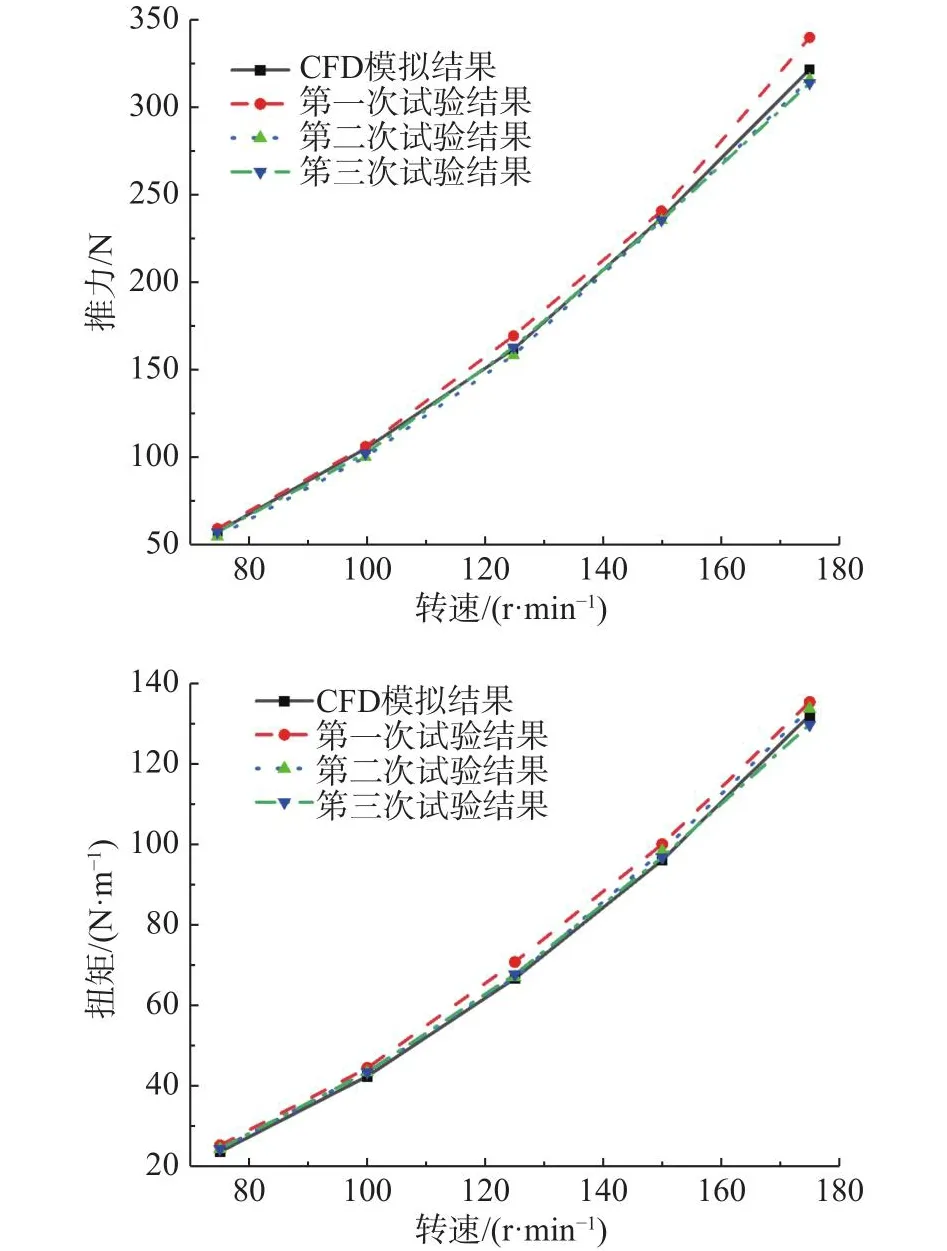
图4 测试数据和仿真数据对比Fig.4 Comparison of experimental and numerical results
3 贝叶斯优化方法
本文使用的高空螺旋桨贝叶斯优化方法流程如图5所示。

图5 高空螺旋桨贝叶斯优化流程Fig.5 BO process for high-altitude propellers
图中初始样本使用拉丁超立方抽样,根据实际需求选择初始样本数量,通过数值模拟来计算螺旋桨气动性能。初始样本通过训练获得初代高斯过程模型。CMP为带约束的目标函数最小值预测准则(constraint minimizing the predicted objectivefunction)[18-19], CEI为 带 约 束 的 改 善 期 望 准 则(constraint expected improvement)[18,20],CMSE 为带约束的均方差准则(constraint mean squared error)[18-19]。遗传算法和以上三种准则共同构成贝叶斯优化的并行加点子优化。子优化可以获得不同加点准则在当前模型下的最优解及对应设计变量,通过数值模拟得到气动性能,并将新的样本点加入样本数据,更新样本数据,训练模型。三种加点准则可以在一次优化中产生三个新样本点,从而提高优化收敛速度。产生于当前模型最优解附近的新样本点,提高了更新后的模型在局部和全局最优解附近的近似精度,这样可以将样本点添加在模型最需要的地方,降低优化时间成本,提高优化效率。这是贝叶斯优化和固定代理模型优化的主要区别,也是贝叶斯优化的优化机制。
贝叶斯优化没有严格的收敛条件,国内外关于其优化终止条件定义的文献较少,也没有统一的标准。本文使用两种终止条件共同判定[13]:
(1)根据样本点距离及其对应目标函数值的差别来定义。
式中,下标“new”代表新加入的样本点,下标“best”代表现有样本中的最优点。当新加入样本点与当前最优样本点之间的距离以及函数值之差相对值小于设定的阀值ε时,优化即可终止。
在设计空间内,高空螺旋桨的优化是一个多峰多谷问题,对于相同的目标函数值,可能有不同解。因此在上述终止条件中,增加了样本点距离的比较,以确保目标函数变化达到要求的阈值时,对应的样本点在同一个峰内,即,只有新样本点与已知最优样本点之间的距离和目标函数变化都很小时才认为优化收敛。
(2)预设的数值模拟最大次数。由于代理模型的使用,单独使用终止条件(1)可能存在一个问题—当优化获得的新样本点恰好在初始最优样本点附近时(即初始最优样本点恰好在初始模型某个局部或全局最优解附近时),可能由于达到收敛阈值而使优化提前终止,但此时模型精度不高,获得的结果并不是最优。为了避免这种可能存在的偶然情况,本文同时使用了终止条件(2)。两种终止条件共同使用,避免了上述偶然情况的发生,使优化能在可接受时长的约束范围内获得较好的结果。
4 基于贝叶斯优化的气动外形设计
本文使用贝叶斯优化方法,对通过叶素/涡流理论优化设计获得的某高空太阳能无人机螺旋桨进行气动优化与验证。设计工况如表3所示。

表3 设计工况Table 3 Design condition
4.1 优化模型
根据螺旋桨参数化方法,确定其几何外形共需8个变量。在确定典型任务工况情况下,计算螺旋桨气动性能还需转速(n)。因此拉丁超立方抽样的变量数为9。当桨径固定时,实际设计变量数为8。本文取样本数量为40。各变量取值范围见表4。
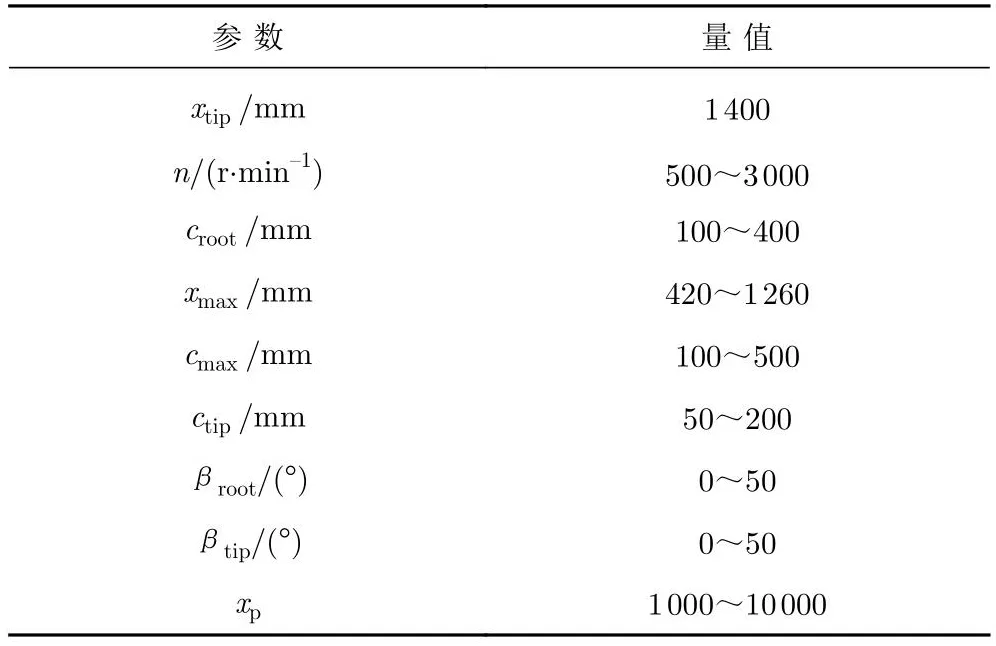
表4 设计变量范围Table 4 Design variable value range
高空螺旋桨气动性能主要有推力(T)、扭矩(M)、功率(P)、效率(η)。其优化问题是在输入功率限制下,使螺旋桨产生的推力最大。其优化数学模型为:
各子优化均使用精英保留遗传算法(elitist reservation genetic algorithm, EGA),种群数量为50,最大代数为1 000。
本文使用的优化终止条件中,新加入样本点目标函数和当前样本最优点目标函数之差的相对值的阈值ε为1 × 10-6。调用精确数值模拟次数最大为300。
4.2 优化结果对比
图6给出了优化目标函数迭代收敛曲线。图中横坐标表示调用数值模拟次数(含初始样本数值模拟时的调用次数),即样本点数量;纵坐标表示用当前样本点训练成的模型优化得到的目标函数值。从图中可以看出,样本点数量约为130,即优化调用90次数值模拟时,优化开始趋于收敛,且在后续再进行的110次子优化中,目标函数不再提升。

图6 优化收敛曲线Fig.6 Optimization convergence curve
优化前后设计变量取值对比如表5,气动外形对比如图7。从优化前后设计变量和气动外形的变化可以看出,优化后的桨叶有更大弦长,最大弦长位置更靠近根部,螺旋桨的面积由0.266 m2增加到0.294 m2;优化后的桨叶从根部到尖部的扭转角变化更大。

表5 优化前后设计变量对比Table 5 Comparison of design variables before and after optimization

图7 优化前后外形对比Fig.7 Shape comparison before and after optimization
图8给出了优化前后螺旋桨在表3所示高度和速度下的气动性能对比。图中横坐标为前进比(λ),由于设计中来流速度和桨径为常量,因此前进比只与转速有关。从图中可以看出,相同前进比下,优化后的螺旋桨在设计点附近具有更高的推力和效率。表6给出了5 kW功率点的性能对比。优化后的螺旋桨在功率点的性能显著提高,推力提高9.24%,效率提高8.13%。优化后,在5 kW设计点转速降低约100 r/min,因此桨尖马赫数减小;但由于桨尖剖面弦长增大,所以桨尖雷诺数增大。
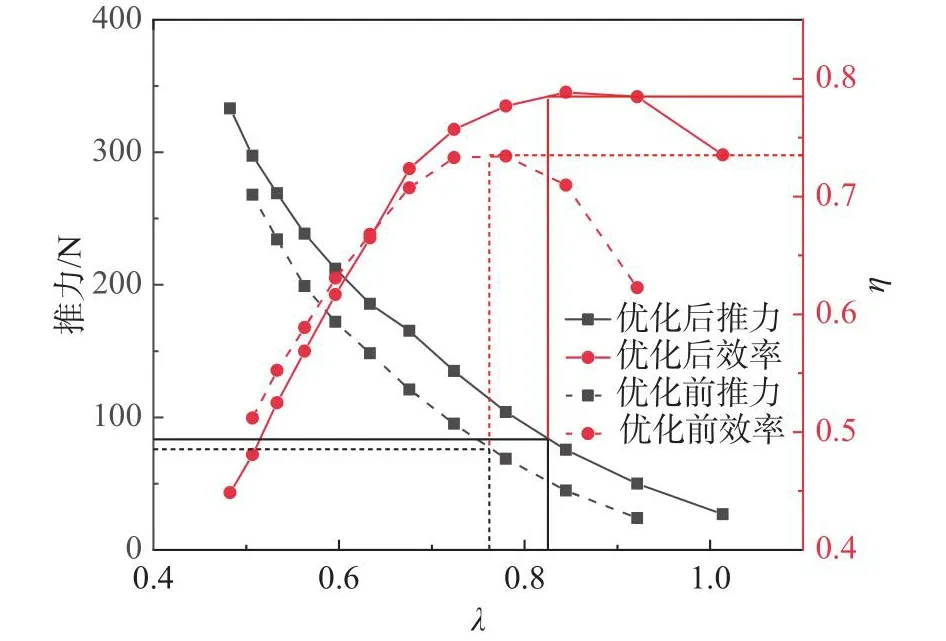
图8 螺旋桨性能对比Fig.8 Comparison of aerodynamic performance

表6 5 kW设计点气动性能对比Table 6 Comparison of aerodynamic performance at 5 kW
在5 kW设计点,优化前后桨叶压力分布如图9所示,流线如图10所示。优化前后桨叶负压均出现在前缘靠近桨尖的位置,压力分布连续性较好,无突变情况,这与螺旋桨旋转时实际压力分布情况相同。优化前桨叶尖部流线不完整,表明在该工况下,气流在桨叶尖部后缘上表面出现提前分离,而优化后的桨叶流线分布较好。

图9 5 kW功率时压力云图对比Fig.9 Comparison of pressure contours at 5 kW power

图10 5 kW功率时流线图对比Fig.10 Comparison of streamlines at 5 kW power
5 结 论
本文从优化耗时和数据精度影响两方面考虑,提出了一种基于贝叶斯优化框架的高空螺旋桨气动外形优化设计方法,并完成高空螺旋桨气动优化设计。研究结果表明:
1)基于贝叶斯优化框架的高空螺旋桨气动外形优化设计方法具有更好的全局收敛性,能在可接受时长内获得更高效的气动外形设计方案。
2)该方法中,加点准则和遗传算法构成的子优化产生新样本点是其优化机制,而并行加点策略则可以有效提高优化的全局收敛性和收敛速度。
3)该方法可以对螺旋桨的气动设计及应用提供工程指导,同时也可以为机翼的设计提供一定的参考和技术支持。
4)该方法中子优化均为单目标优化,每次优化中新样本点的个数取决于加点准则的个数,这在提高优化效率方面仍然比较有限。若考虑将子优化转换为多目标优化,有望大幅降低优化迭代次数、提高优化效率、增强应用便捷性。这将作为后续研究的重要内容。
