基于卡尔曼滤波的翼型表面压力实时重构方法
2023-05-09刘余丹周楷文刘应征
刘余丹,周楷文,刘应征,温 新,*
(1.上海交通大学 机械与动力工程学院,上海 200240;2.空气动力学国家重点实验室,绵阳 621000)
0 引 言
飞行器实时控制是实现飞行器姿态调整、提高飞行器机动性能的有效方法之一,而飞行器环境参数的感知是实现其飞行控制的基础。飞行器在飞行过程中往往面临着复杂的非定常流动问题,但传统的传感器设置方案,如惯性测量装置、磁力仪、风速仪等,受测量技术、安装空间等限制,仅能感知到局部的、离散的参数,难以为飞行操纵系统及时提供飞行控制所需的全部信息。在此情况下,难以对飞行器的关键气动参数进行精准识别,进而难以实现运行监测与主动控制。因此,利用有限的观测数据实时感知飞行器周围流场的全貌具有重要意义。
许多学者研究了如何通过有限的测量数据重建整个流场的问题。其中,一部分学者的研究主要基于Everson和Sirovich[1]在1995年提出的一种恢复缺失数据的gappy POD方法展开。gappy POD方法可用于将风洞实验所获得的有限表面压力测量数据与CFD计算数据融合,以感知流场的全貌[2],但gappy POD所采用的求解流场重构系数的最小二乘法对噪声较为敏感。还有一些学者基于机器学习方法进行了研究。Deng等[3]采用长短时间序列(LSTM)神经网络建立离散测量点数据与POD模态系数之间的关系,进而实现流场全重构。但机器学习的方法存在缺乏物理解释性、过拟合等问题。
Candes等[4]2006年提出的压缩感知理论指出,如果一个信号在某一特定基上具有稀疏表示,则该信号可以从相对较少的随机采样中得到恢复,该结论为从有限的测量数据实现流场实时重构指明了新的方向。此前已有部分学者尝试将压缩感知理论应用于流场重构。Huang[5]对压缩感知在航空航天应用中的潜力进行了探讨。Zhao等[6]提出了一种基于压缩感知重构翼型表面压力的精细方法,以获得翼型表面完整的压力分布信息以及精确的升力和力矩特性。Bright等[7]利用压缩感知技术,通过圆柱体表面的有限离散压力测量数据重构圆柱体周围的流动特性。Wen等[8]开发了一种基于压缩感知的数据挖掘方法,从低速圆柱尾流诱导的非定常压力场的高噪声测量中对流场数据进行重构。但基于压缩感知的流场重构方法同样不具鲁棒性,易受噪声影响。
本文所提出的基于压缩感知与卡尔曼滤波器的实时流场重构方法,采用卡尔曼滤波器,针对基于压缩感知的流场重构方法进行改进。该重构方法具体可分为线上和线下两个部分:线下全场采样,通过本征正交分解建立数据库;线上稀疏采样,通过压缩感知优化重构系数,然后采用基于内嵌动态模态分解的卡尔曼滤波器对所求解时间系数进行实时去噪,提高重构方法的鲁棒性。
1 重构方法
基于压缩感知与卡尔曼滤波器的实时流场重构方法流程图如图1所示。
1.1 本征正交分解
本征正交分解(POD)是提取离散数据主导特征的有效方法[9-10]。本文使用POD对带有噪声的全场测量数据Pfull进行处理,构建主导空间模态 ψ 与对应时间系数afull组成的线下数据库,该过程对应于图1中红色A所标记的过程。采用POD可将流场Pfull分解为以下形式:

图1 重构方法流程Fig.1 Outline of reconstruction method
其中:k表示流场快照序号;M表示流场快照总数;表示流场快照均值; ψi表示POD主导空间模态;表示主导模态对应的POD时间系数。该分解过程可利用奇异值分解(SVD)实现:
其中:λ表示各POD模态能量贡献。
以能量贡献排序的前几阶POD模态捕获了流场的主导流动结构,可用于构建原始流场的低阶近似模型:
其中:m表示低阶模型维度。构建低阶模型可简化对复杂流场的描述,同时,通过选择主导空间模态并忽略其他不重要的模态,可在一定程度上起到滤除数据噪声的效果。
1.2 压缩感知
压缩感知是一种寻找欠定线性系统的稀疏解的技术,已在各个领域得到广泛应用[11-13]。压缩感知理论指出,对于稀疏信号或可压缩信号,可通过远低于奈奎斯特采样率的采样数据实现其精确重构。
本文通过求解L1范数下的最优化问题求解流场重构系数acs:
其中:Pscattered表示线上稀疏采样数据;ψ表示线下所得POD主导模态;矩阵 ϕ存储离散传感器的位置信息。详情参见文献[14]。最终,可通过流场重构系数与POD主导模态的线性组合实现全场数据的重构:
其中:m表示用于实现流场重构的主导模态数量。
1.3 卡尔曼滤波器
卡尔曼滤波器提供了一种基于线性系统模型与测量数据对系统状态进行最优估计的方法[15-16]。本文引入卡尔曼滤波器对压缩感知求解所得流场重构系数acs进行实时去噪,进一步提高流场重构方法的鲁棒性。卡尔曼滤波器中系统的线性模型可表示为:
其中:x表示系统状态;A表示系统的线性状态转换矩阵;w表示协方差为Q的高斯分布的系统误差。卡尔曼滤波器中的测量过程可表示为:
其中:y表示测量结果;H表示观测矩阵;v表示协方差为R的高斯分布的测量误差。
卡尔曼滤波器包含预估、矫正两个步骤。预估步为:
矫正步为:
其中:上标 p表 示预估值;上标 c 表示校正值;F表示预估协方差矩阵;K表示卡尔曼增益。本文中,所要估测的系统状态为POD时间系数a。
1.4 动态模态分解
采用动态模态分解构建卡尔曼滤波器的线性系统模型,对非线性流动问题进行线性化近似[17]:
本文中,
矩阵A的最佳形式可以表示为:
其中:上标+表示Moore-Penrose伪逆。
2 数据准备
采用商业软件ANSYS模拟处于圆柱尾涡影响下的翼型表面压力变化,CFD模型示意图如图2所示,选用k-ω SST作为湍流模型,来流速度设置为30 m/s,翼型表面随机设置12个离散压力传感器,传感器布置位置如图中红色·所示。

图2 CFD模拟模型示意图及离散传感器布置位置Fig.2 Schematic diagram of CFD simulation model and deployment of discrete sensors
为模拟线下全场采样中可能产生的噪声问题,对所模拟翼型表面压力数据加入标准差为流场参数均值10%的高斯噪声,所得单周期无噪声与含噪声流场的演化过程对比如图3所示。同时,为模拟线上稀疏采样过程中可能产生的噪声问题,对所合成离散数据加入标准差为流场参数均值10%的高斯噪声,所得单周期无噪声和有噪声的离散数据随时间变化的曲线图如图4所示。
3 方法验证
采用POD对线下所获得含有噪声的全场数据Pfull进行处理,计算其主导空间模态 ψ 与其对应的时间系数afull。前四阶POD空间模态和时间系数如图5所示。POD主导空间模态捕获了流场的主要流动特征,与之对应的时间系数描述了其在时间上的动态演变。
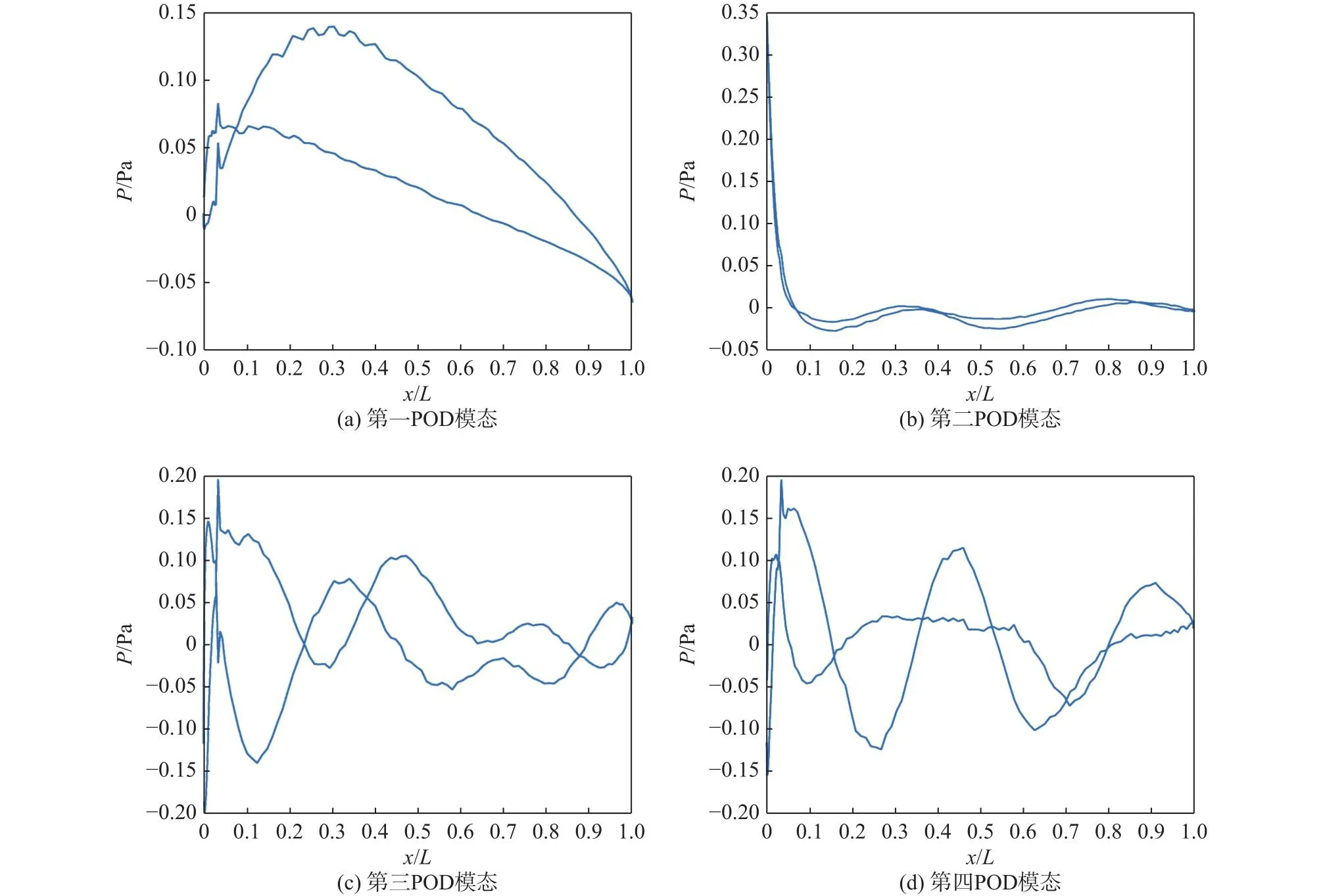
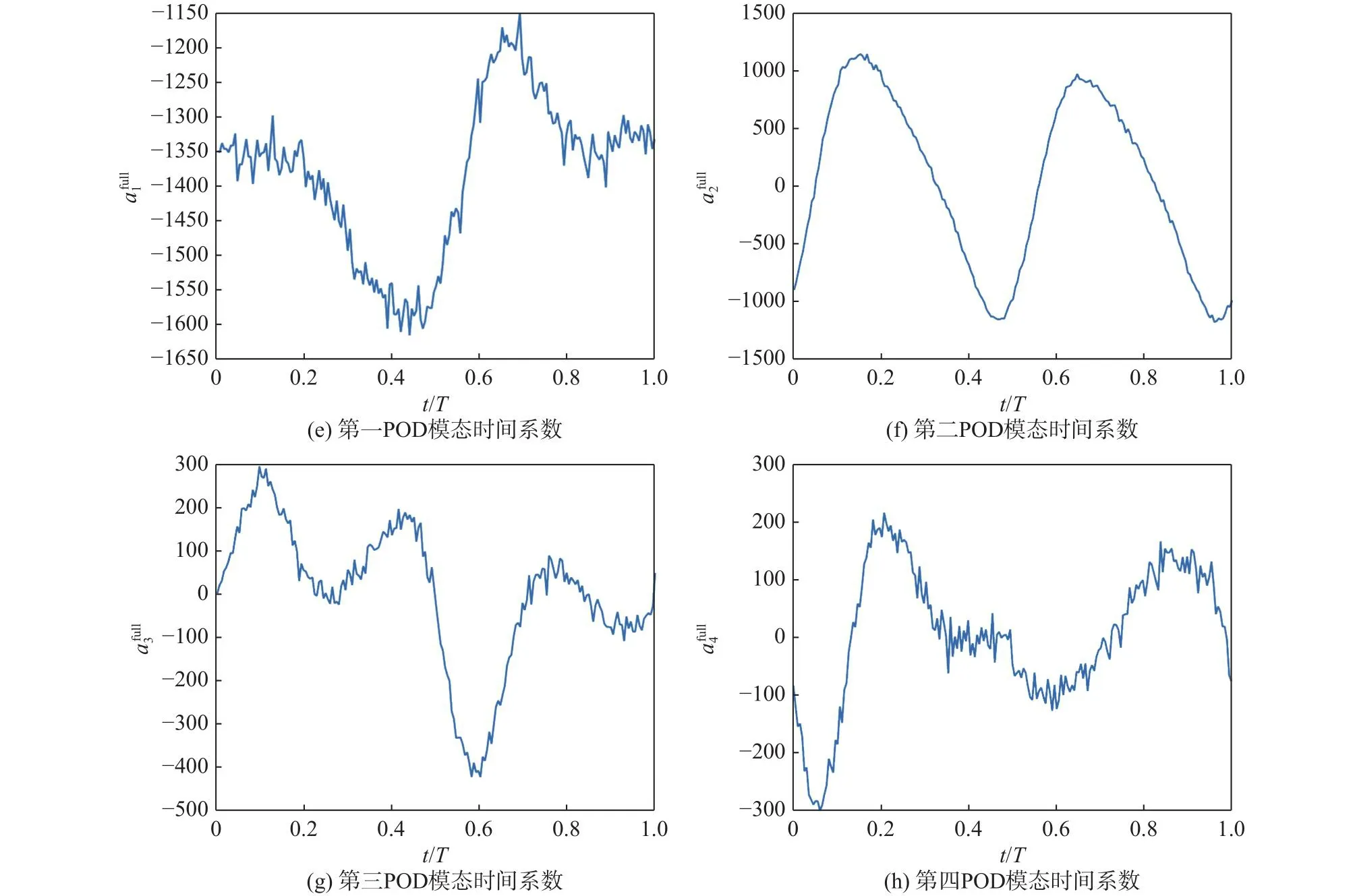
图5 前4阶POD空间模态及其对应的时间系数Fig.5 The first four POD spatial modes and corresponding time coefficients
选取前十阶POD模态作为压缩感知的稀疏基,以含有噪声的线上采样稀疏数据Pscattered作为观测值,在L1范数最小化的条件下求解最优时间系数acs。压缩感知计算所得前四阶模态对应的时间系数如图6所示,同样计算所得时间系数严重扭曲,含有大量噪声。直接通过这些含有大量噪声的时间系数对流场进行重构,重构所得结果如图7所示,与真实翼型表面压力分布情况存在较大不符,无法满足对翼型表面压力进行全场感知的要求。

图6 压缩感知所得前4阶模态时间系数Fig.6 The first four modal time coefficients obtained by compressed sensing

图7 压缩感知所重构翼型表面压力Fig.7 Airfoil surface pressure reconstructed by compressed sensing
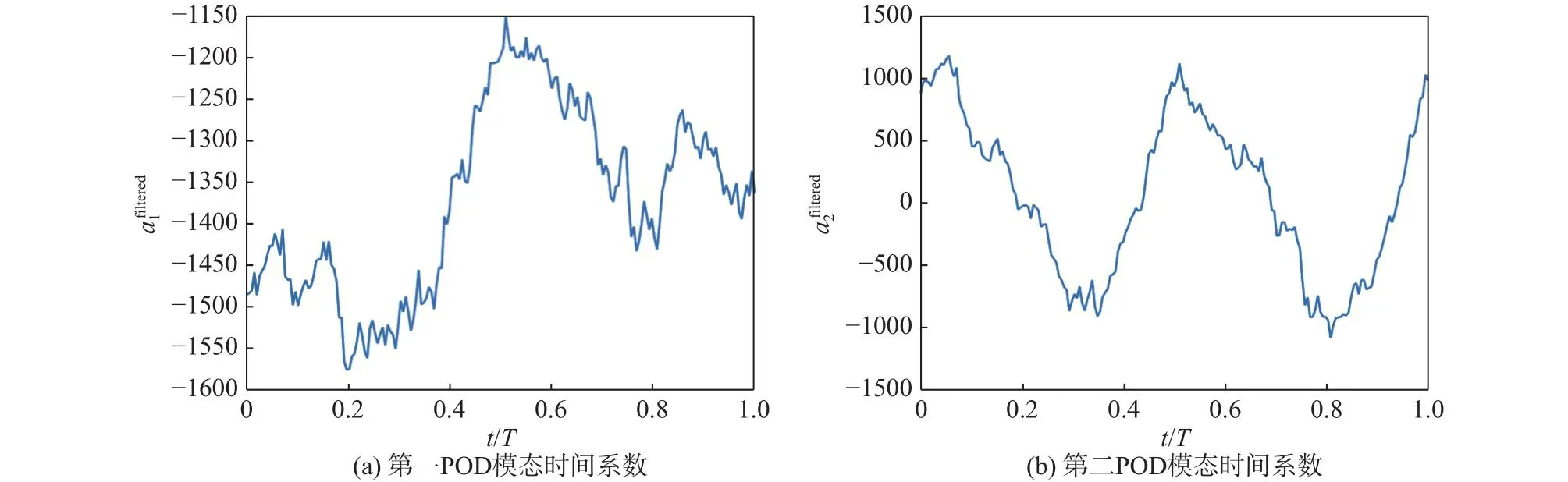
为了解决上述噪声干扰问题,在压缩感知流场重构方法的基础上引入了卡尔曼滤波器。采用DMD对线下所得流场时间系数进行处理,以DMD所得线性近似模型x′=Ax作为卡尔曼滤波器的系统模型;以线上压缩感知计算得到的含有噪声的时间系数作为观测值进行滤波。卡尔曼滤波器中过程噪声方差矩阵Q和 测量噪声方差矩阵R应基于系统模型误差与传感器测量误差的统计学信息设置,本文此处分别设置为0.0075Eeye(m)和 2Eeye(m),其中Eeye(m)表示m阶单位矩阵。经卡尔曼滤波器实时去噪后所得的时间系数得到显著平滑,如图8所示。利用滤波后的时间系数进行重构,重构所得结果如图9所示,与各时刻翼型表面真实压力分布吻合良好,满足对翼型表面压力进行全场感知的要求。

图8 经卡尔曼滤波器处理后前4阶模态时间系数Fig.8 The first four modal time coefficients processed by Kalman filter

图9 经卡尔曼滤波器所重构翼型表面压力Fig.9 Airfoil surface pressure reconstructed by Kalman filter
基于翼型表面压力数据积分可计算其升力l。经压缩感知所重构升力和卡尔曼滤波器处理所重构升力与真实升力变化曲线的对比如图10所示。可以看出,经压缩感知所重构升力在总体变化趋势上与真实情况基本一致,但存在较严重的噪声问题,无法满足飞行器飞行过程中精准感知的要求。在采用卡尔曼滤波器进行处理之后,重构结果与真实值之间的差异显著降低,重构结果基本满足对升力进行准确感知的要求。

图10 重构升力系数对比Fig.10 Comparison of lift coefficients reconstructed by compressed sensing and Kalman filter
为量化卡尔曼滤波器对升力重构准确性的提升效果,定义升力的重构误差为:
其中:M表示流场快照总数;lrecon表示重构所得升力;ltruth表示真实升力。经压缩感知所重构流场与经卡尔曼滤波器处理后所重构升力误差分别为6.39%和18.15%,误差相较下降64.79%
4 结 论
本文提出了一种鲁棒的基于数据融合的实时流场重构方法,可以从有限的测量数据中实现全场数据的重构。通过压缩感知和DMD线性模型内嵌的卡尔曼滤波器,显著增强了其鲁棒性,有效抑制了噪声的影响。
以翼型模拟数据为例测试了该方法的性能,并对是否采用卡尔曼滤波器进行重构的结果进行了量化分析。对于翼型表面压力数据,升力重构误差从18.15%减小到6.39%,相较下降64.79%。
另外值得注意的是,卡尔曼滤波器的成功应用在很大程度上依赖于模型误差方差矩阵及传感器的误差方差矩阵的准确性,而在实际应用中方差矩阵很难确定。为了对此进行改进,我们目前正在开发基于DMD线性模型内嵌的自适应卡尔曼滤波器,引入对噪声统计特性的实时动态估测,解决实际应用中误差方差矩阵难以准确估测的问题。
此外,本文目前所采用POD、DMD、卡尔曼滤波等流场分解与建模方法均为线性化方法,且DMD线性建模方法仅对较为简单的周期性流动问题具有较好的适用性。后期考虑采用卷积神经网络、扩展DMD、集合卡尔曼滤波等非线性建模方法,进一步提高该方法的普适性。
