电动无人驾驶配送货运车辆路径优化研究

温欣琪，唐鑫琦

（长安大学 汽车学院，陕西 西安 710064）

现如今，随着我国经济高速稳定发展，城市化进程的迅速推进，交通领域的不断发展，消费模式迎来了巨大的转变。与此同时，传统内燃机汽车的应用带来了一些负面效应，如：消耗了大量的不可再生能源、产生大量的噪声污染、汽车尾气的排放加剧温室效应等。随着人们社会环境意识的不断增长，无人驾驶技术的逐渐发展和成熟，无人驾驶电动汽车具有绿色、高能源利用率、低噪音、自动化、无人化、信息化的优势被广泛看好，智能无人物流具有成本低、效率高的优势逐渐成为未来发展的趋势。然而由于电动汽车电池和充电技术发展尚不完善，使得无人驾驶电动物流车的标定续驶里程普遍不高，中途充电的时间普遍偏长，并且由于充电站的数量较少，且部分充电站的位置布置不适用于物流，再加上城市交通拥堵、载货量、司机操纵特性、气候等外界环境等因素的复杂影响，导致无人驾驶电动物流车的实际续驶里程小于标定续驶里程。这就对电动配送货运车辆路径优化提出了更高的要求。因此，将无人驾驶技术和具有广泛优势的电动汽车结合运用于物流配送中，并研究其路径优化问题是很有必要的。

SCHNEIDER[1]等在2013 年研究了带时间窗的电动车辆路径优化问题（Electric Vehicle Routing Problem with Time Windows, EVRP-TW），其中车辆必须在充电站处才能充电服务，将电池电量消耗表示成了车辆行驶距离的线性函数。YANG和SUN[2]在2015 年首次提出了纯电动物流汽车的充电站选址的车辆路径优化问题（Vehicle Routing Problem, VRP），充分考虑了电动物流车的特点，对充电站的位置进行了关注。DESAULNIERS[3]在2016 年研究了多次充电和单次充电的、完全充满和部分充电的电动车辆路径优化问题（Electric-Vehicle Routing Problem, EVRP）。SCHIFFER 和WALTHER[4]在2017 年提出了电动车充电站位置选择与路线优化问题（Electric-Vehicle Location Routing Problem, E-LRP）。MERVE K 和BÜLENT Ç[5]在2018 年研究了带时间窗的电动汽车路径问题，提出车站可以配备不同的电源充电器，以提供不同的功率，并讨论了相应的数学方法。RUBIANO[6]等在2019 年研究了考虑行驶距离约束和随机行程时间下的EVRP 问题，提出了一种简单启发式算法。目前EVRP 问题处于不断完善的阶段，关于电动物流车路径优化的方法逐渐优化。然而国外学者对于将无人驾驶技术运用到物流配送中后产生的路径优化问题的研究并不多，对于解决其算法的设计也缺乏研究。

汪丽颖[7]在2016 年研究了电动车充电站策略和VRP 问题，将自适应变领域搜索和禁忌搜索混合，提出了一种新型启发式求解算法，并得出快速充电设施和超快速充电设施的组合表现更有利于实现系统总成本最优的条件。沈续昌[8]在2018年建立了考虑货物重量的EVRP 问题的新模型，同时考虑了运输距离，车身自重，货物载重量对电能的消耗，模型中还考虑了取货送货的实际问题。张鹏威[9]在2019 年构建了有限充电设施下的多配送中心的EVRP 问题，设计了分散搜索算法来求解，并提出将配送中心作为充电站的方式来提高效率，缓解充电设施不足的影响。无人驾驶EVRP 问题以及无人配送路径优化逐渐成为配送的一个重要课题，但国内相关的研究文献目前也较少，熊会元[10]等在2019 年研究得出电动无人集卡可以推动智慧物流的发展。胡觉亮[11]等在2020年研究了城市物流中电动无人车配送优化的问题，明确使用电动无人车进行城市物流配送可以提高效率并降低成本。目前无人驾驶EVRP 问题面临着核心模型构建不够完善和路径规划算法有待进一步研究的问题。

本文在前人的研究基础上，进一步对电动无人驾驶车辆路径优化问题进行研究，提出了本文研究的无人驾驶电动物流车路径优化问题的数学模型，运用LINGO 软件进行小规模算例测试，以验证模型的合理性。并将用于求解车辆路径优化问题的节约里程法进行改进，用于解决电动车辆路径优化问题。运用MATLAB 软件求解验证模型的小规模算例，来证明算法的可行性，求解一个大规模算例，证明本文算法可以求出合适的解，并发现设计算法的不足之处。

1 模型构建

本文研究的是电动无人驾驶的VRP 问题，这是在传统的VRP 问题、EVRP 问题上的拓展，不仅考虑了电动车辆路径优化的约束条件，还加入了无人驾驶产生的新的约束条件。并且由于电动无人驾驶配送货运车辆相较于普通电动物流车最大的优势在于降低运营成本、人力成本，可以实现全天配送，防风雨，有效解决城乡“最后一公里”配送问题，提高了运输配送效率，从而进一步降低了单位配送里程的成本。

1.1 模型声明

现实中的配送问题是十分复杂且灵活的，不利于研究，为此本文构建的模型对现实的配送问题进行了简化，为此设立了如下的假设条件：

1）各个节点的位置是已知的，由坐标(x,y)表示，并由此可以计算出任意俩节点间的距离；

2）各个客户点的需求是已知的，并且是固定的，不会发生变化，且每个客户点的需求量要一次配送完成，不进行二次配送，即需求是不可拆分的；

3）参与配送的电动无人驾驶配送车辆的车型是固定单一的，每辆车的最大载重量和电池的容量是固定的，并且假设百公里耗电量是一给定值，并且耗电量随行驶里程的增加成正比增大；

4）车辆配送的成本总体上随着配送距离的增加而升高，即车辆配送的成本和配送距离呈正比关系；

5）单配送中心进行配送，即所有参与配送的车辆从一个配送中心出发进行配送，配送完成后返回该配送中心；

6）电动车辆从配送中心发出时的电池电量应该属于充满的状态，并且在客户点处服务时电量不消耗；

7）配送服务无时间窗的要求，即在任意时刻送达即可。

为了更加清晰地描述构建的电动无人驾驶配送货运车辆路径优化模型，本文对模型设计到的集合、变量、参数做了如下说明，如表1 所示。

1.2 模型构建

由于电动无人驾驶配送货运车辆的最大优势体现在成本上面，因此，本文选取总成本最低作为研究的目标函数。车辆配送的成本总体上随着配送距离的增加而升高，可以认为车辆配送的成本和配送距离成正比关系，将正比系数记为N，便可以得到如下的目标函数：

电动无人驾驶配送货运车辆有最大的额定载质量，超载容易增加事故发生率，也使车辆更易受损，增加维修成本，因此，要限制车辆的装载量小于额定载质量。建立的约束可以用如下的数学公式表示：

配送车辆在配送中心装载货物后，出发完成配送任务，并且在完成配送任务后，要回到配送中心，进行卸货或再次装载。同时要保证开出的车辆要全部回到配送中心。本文假设有一个配送中心，因此，建立的约束可以用如下的数学公式表示：

电动物流车在行驶的过程中，电池的电量在不断地消耗，已知电动物流车的电池容量为C，每单位行驶里程电池的耗电量为h。电动物流车在从配送中心出发的时候，电池电量应该是充满的。建立的约束可以用如下的数学公式表示：

电动物流车的电池电量低于某一值时，电动物流车容易因没电而停驶，如若停驶时距离充电站距离过远，将影响配送效率。并且对于电动车来说，在配送的过程中，电池的电量会有所消耗，因此，到达下一个目的地的电量应该小于出发目的地的电池电量。因此，要对到达节点的电量进行计算，计算的公式可以用如下的数学公式表示：

无人驾驶的电动物流车还有一个特点，有人驾驶时，驾驶人员可以自行观察电池电量，选择合理的方式，合理的时间前往充电，而无人驾驶的电动物流车就需要程序来判断充电的时间，为此需建立一个约束。查阅特斯拉电池系统的电池曲线的测试实验结果的相关资料可知，25%～75%的充放，是比较合理的，对电池使用寿命的影响较小。本文选取30%，即电池电量低于0.3C就应该返回配送中心进行充电。建立的约束可以用如下的数学公式表示：

根据确定的假设和定义的参数，参考上文的目标函数以及约束条件，建立的电动无人驾驶配送货运车辆路径优化的数学模型如下：

式（7）为目标函数，表示总成本最低。式（8）为每个顾客点都需要被服务，且只能被服务一次；式（9）为流量平衡；式（10）为每次配送都以配送中心为起点，以配送中心为终点，并且出入库车辆的数目一定；式（11）为若车辆k服务节点i，则让其对应的r为1；式（12）为载货量约束。式（13）为从配送中心和充电站离开的时候满电量；式（14）为在客户点处不消耗电量；式（15）为电动车辆的电量不能低于0.3C，不能大于C；式（16）用来计算车辆到达任意节点的电量；式（18）定义了一个辅助变量z，并要求它非负；式（17）和式（18）限制线路中产生子回路；式（19）定义了一个0,1 决策变量x；式（20）定义了一个0,1非决策变量r；式（21）定义了一个连续变量y，并对它的取值范围进行了约束。

1.3 模型验证

本文选取一小规模算例，用LINGO 软件对算例进行计算，来验证模型的合理性。本文考虑随机生成客户点，同时对时间窗不进行限制要求，因此，将Solomon 算例中的R 系列的R107 作为小规模算例，选取R107 中的7 个点，选取6 个分散的点作为客户点。其中0 点为配送中心，1—6点为配送客户点，这样就形成了配送中心位于客户点中心，各个客户点分散分布，各个方位都距离配送中心合理的小规模算例，具体参数信息如表2 所示。

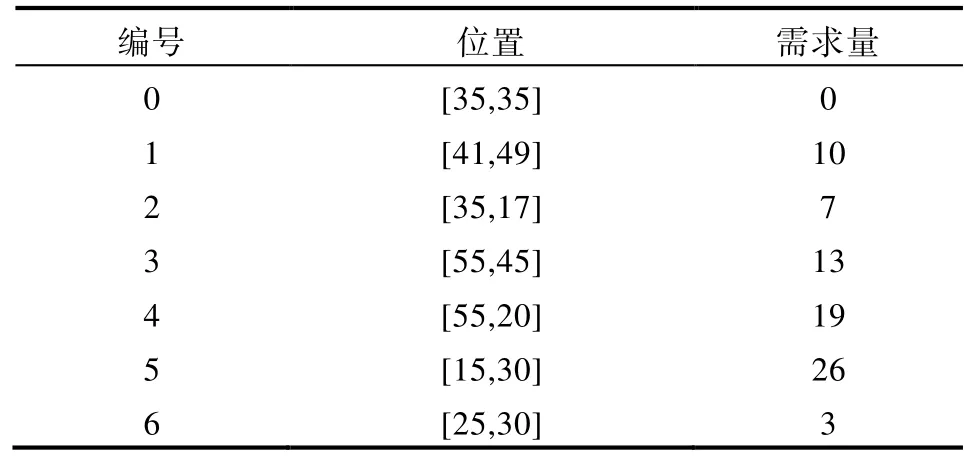
表2 各节点的测试数据

考虑实际情况以及模型验证和简洁合理性，对模型中涉及的数学参数进行了赋值，以用于模型求解，主要的数学参数有最大载重量，电动物流车的电池容量，车辆运输成本和车辆行驶距离的正比系数，每单位行驶里程的耗电量，参与配送的无人驾驶电动物流车的车辆数目，具体的参数取值如表3 所示。

表3 无人驾驶电动物流车的参数信息

运用LINGO 软件对选取的小规模算例进行求解分析，将本文建立的电动无人驾驶配送货运车辆路径优化模型转化为LINGO 语言，对1 个配送中心，6 个客户点，3 辆配送车辆构成的小规模算例进行求解，在迭代2 434 次后，求得一个可行解78.586，即表示最短配送里程为157 km，最低成本是78.6 元/km。

求得的配送结果是配送车辆1 从配送中心发出，按顺序到客户点3、1 进行配送，最后回到配送中心，即0→3→1→0；配送车辆2 从配送中心发出，按顺序前往客户点6、5 进行配送，最后返回配送中心，即0→6→5→0；配送车辆3 从配送中心出发，按顺序前往客户点4、2 进行配送，最后返回配送中心，即0→4→2→0。运用AutoCAD绘图软件绘制的配送路线以及各个节点的到达顺序的示意图如图1 所示。

图1 小规模算例求解结果

2 算法设计

2.1 算法流程

本文研究电动无人驾驶配送货运车辆路径优化问题采取传统启发式算法中的节约法。对比传统的VRP 问题，多出了电量的约束，因此，要对传统的节约里程法进行优化，本文使用的改进的节约法，在计算出节约里程数并且排序后，考察载货量约束和电量约束进行路径划分。具体的考察方式是在判断是否载重量约束的时候，同时判断是否满足电量约束，如果两个条件都满足，则选择该点，输出优化的路径，如果不满足其中任意一项要求，则需要舍弃该点。

本文所研究的带电量约束的电动无人驾驶配送车辆路径优化模型的节约里程法的流程如图2所示。

图2 算法流程图

2.2 算法验证

该小规模算例与上一章节的小规模算例为同一个算例，运用设计的改进的节约里程法，运用MATLAB 软件，编程实现对该小规模算例的求解。将运用算法求解出来的结果，与LINGO 软件的求解结果进行比较，可以判断设计的算法的合理性。如果二者相差的结果不大，并且运用算法求解出来的结果更优，则说明设计的算法是合理的，可以求解出带电量约束和载重量约束的EVRP 问题，如果结果相差很大，说明算法还需要改进。

如图3 所示，由运行结果可知运行线路为车辆1 的路线为0→2→1→3→4→6→0，车辆2 的路线为0→5→0。最低成本为79.076 元/km。对比LINGO 软件的求解结果可知，配送线路发生了变化，分析其原因为LINGO 求解时使用了提供的所有车辆，而使用的算法设计时，在满足电量要求的情况下，只要一条路线上的配送总量没有超出车辆的载重量，就会一直进行配送服务，直至到达车辆的载重量。LINGO 软件求解的最优解为78.586，对比算法求解的最优解79.076 发现结果相近，表明算法是可行的。

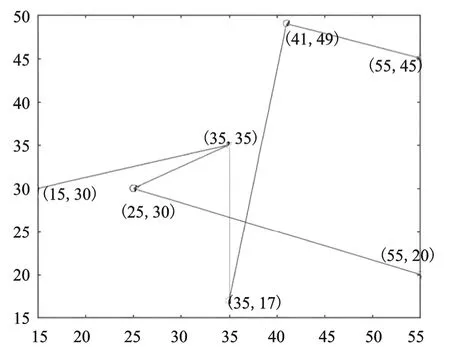
图3 MATLAB 小规模算例求解结果

2.3 算法应用

本文选取一大规模算例，用MATLAB 软件对大规模算例进行分析计算，并对计算的结果进行分析讨论。本文选取与R107 相近的R109 作为大规模算例的数据。R109 数据中包含101 个节点，只取用横坐标、纵坐标、货物需求量。选取R109中的50 个点，其中1 点为配送中心，2—50 点为配送客户点，这样就形成了配送中心位于客户点中心，各个方位客户点距离配送中心位置合理的大规模算例，具体参数信息如表4 所示。

表4 无人驾驶电动物流车的参数信息

对大规模算例进行求解，得到其求解的最优结果，最低成本是402.295 7 元/km。大规模算例的MATLAB 求解结果如图4 所示。

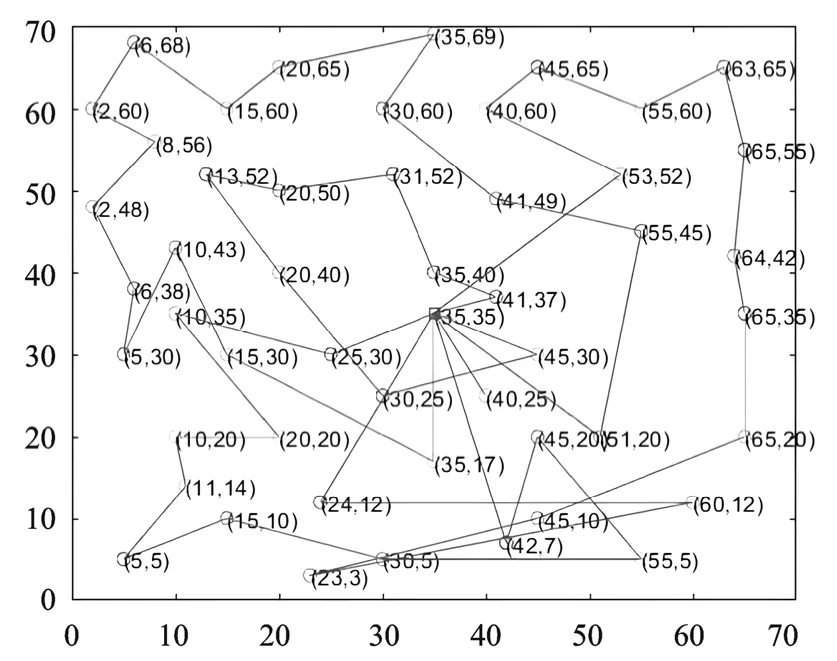
图4 MATLAB 大规模算例求解结果

大规模算例的运行结果如图4 所示，完成配送任务需要5 辆车，配送的最短路程数为804.6 km，配送的最低成本为402.3 元/km。根据求得的结果发现算法可以求出合理的解，然而在配送的过程中由于算法本身计算过程所限，将无法合理地利用每一辆车，使每一辆车的配送任务基本相同，不至于使某些车辆的任务繁重，某些车辆的配送任务太少，而浪费某些车辆的利用空间，增加时间成本。

3 结论

本文考察了电动物流车及无人驾驶技术的应用，发现无人驾驶配送货运电动车辆应用于配送过程中有成本低、效率高、信息化、现代化等显著的优势。本文研究的是有电量约束的单一车型的，无时间窗约束的EVRP 问题。

在学习借鉴前人的研究内容的基础上，本文提出了自己的带有载重量约束，电量约束的车辆路径优化问题的数学模型，运用LINGO 软件对一个小规模的算例进行求解，验证了建立的数学模型是可行的。提出了具有电量约束的改进的节约里程法，并用MATLAB 软件对算法进行编程。在算法设计完成后，对上一章求解过的小规模算例进行再次求解，对比求解结果，确认了算法的可行性、合理性。并运用设计好的算法对一个大规模算例进行求解，分析其结果。

研究的局限性在于，在数学模型构建中只考虑了电量约束，载重量约束和一些基础的约束，未涉及充电站，时间窗限制，与现实生活中的实际配送情况不够贴合。并且在设计算法进行求解时，选择入门的节约里程法。在未来可以进一步丰富模型，选择遗传算法，蚁群算法等一些可以解决更复杂问题的复杂算法。