车用双层微通道散热器热性能的优化研究

张永栋，蒋翠翠，郑少鹏

（广东交通职业技术学院 汽车与工程机械学院，广东 广州 510640）

随着纯电动汽车芯片性能的快速提高，散热不足已成为电子技术发展的瓶颈。当热流密度超过100 W/cm2时，传统空气冷却技术无法满足散热需求，取而代之的是液体冷却技术[1]。在高通量液冷散热装置中，微通道散热器（Micro-channel Heat Sink, MHS）因为具有较大的传热面积与体积比，被认为是改善散热性能的最佳方法之一[2]。微通道散热器作为一种高性能散热装置，可以承受高达790 W/cm2的热通量，极大地提高超高速超大规模集成电路的可行性[3]。文献[4-5]提出了双层微通道散热器（Double Micro-channel Heat Sink,DMHS）的概念，进一步提升微通道散热器的散热性能，并降低所需的压降和泵送功率。为使双层微通道散热器达到更好的整体热性能，本文在一定的约束条件下，以最小热阻为目标，利用响应曲面法对结构进行了优化设计，获得了良好的效果。

1 双层微通道散热器整体结构

硅基微通道散热器在汽车芯片领域应用广泛。因此，本文选择硅作为散热器基本材料。冷却液选择去离子水（初始温度为300 K），因其优越的物理和热力学性能而被广泛选为冷却剂。双层微通道散热器如图1 所示，散热器由矩形鳍片组成，整体高度包括上下层通道高度、顶板厚度、中间板厚度和基板厚度组成，整体宽度12 mm，长度15 mm，原始尺寸如表1 所示。热源布置在散热器下方，两者紧密连接，不考虑热阻影响，上下层流体流动方向相同。

表1 两种原尺寸双层微通道散热器结构参数 单位：μm

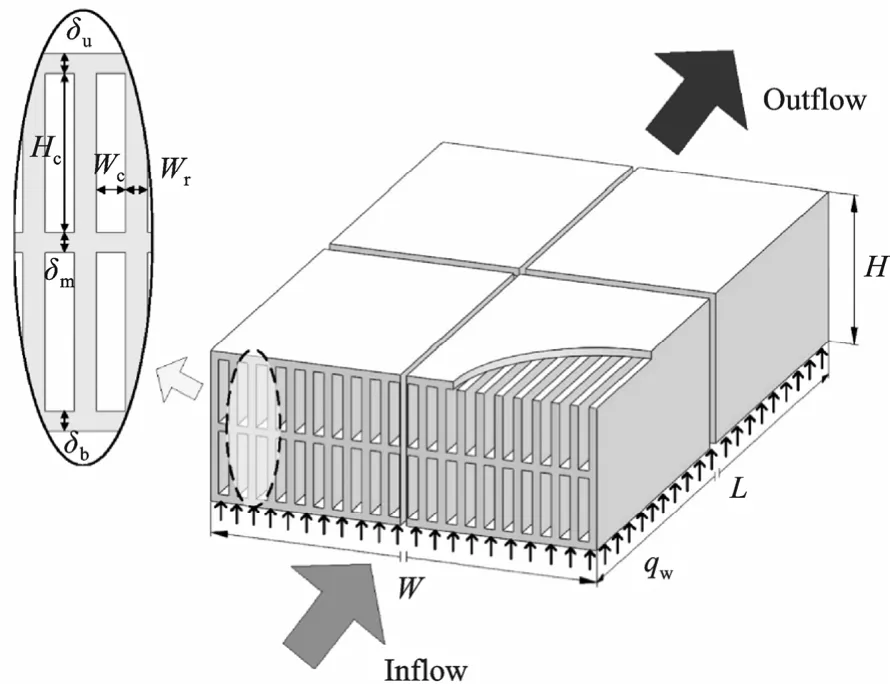
图1 双层微通道散热器结构

图1 中，Wc,u、Wr,u、Hc,u、Wc,l、Wr,l、Hc,l分别是双层微通道散热器上层通道宽度、上层鳍片厚度、上层高度，下层通道宽度、下层鳍片厚度、下层高度；H为散热器整体高度，δu为顶板厚度，δm为中间板厚度，δb为基板厚度。

2 研究方法

由于双层微通道散热器结构参数与热性能间不存在明确的函数关系，所以本文引入响应曲面法（Response Surface Methodology, RSM），建立热性能参数与结构参数间的回归模型，通过对回归模型的优化得到最佳结果。

RSM 是数学、实验设计和统计分析相结合的方法，该技术利用合理的实验设计，找出对结果有显著响应的参数，并采用多元二次回归方程建立自变量和因变量之间的数学模型，通过对回归方程的分析寻找最优结构参数。RAHIMI-GORJI等人[6]采用RSM 对单层微通道散热器通道几何结构进行优化设计，取得了良好的效果，证明RSM在微通道散热器结构优化的有效性。ZHOU 等人[7]也采用RSM 结合有限体积法对一种呈正弦波结构微通道的几何参数进行了优化，发现该方法具有高效、准确的特点，对非规则传热结构的优化具有广泛的应用前景。

实践证明使用RSM 可以减少解决目标所需的时间，并节省大量资源。本文使用计算流体力学（Computational Fluid Dynamics, CFD）软件代替实验，结合CFD 优化双层微通道结构。文中采用二阶模型，即响应因变量y包含线性项、平方项和叉积项三部分，定义为[8]

式中，xi、xj为设计变量，本文中设计变量为双层散热器结构参数，a是调谐参数，下标i代表响应观测中的观测单位，n是变量的数量。

大量研究表明，微通道散热器在实际工程应用更加看重泵功率和热阻的关系，微通道散热器泵工定义为

式中，P为微通道散热器泵功；A为散热器通道截面积；Δp为散热器压降损失。

总热阻定义为

式中，Tw,max为底板的最高温度；Tin为冷却液入口温度；Ab为计算域的底板面积，热通量为恒定值：qw=2×106W/m2。

3 优化方案

本文采用数值模拟结合曲面响应方法开展研究，为了简化模型和网格数量，节约计算时间，考虑到图1 所示的周期性和对称性条件，根据双层微通道散热器的结构特征，提取一个对称单元尺寸作为计算域单元尺寸为（0.24×0.95×27）mm，顶板、基板、中间隔板厚度为50 μm，散热器上下层具有固定的鰭片间距，分别为80 μm、120 μm，上下层通道总高度为800 μm，以冷却液入口流速、下层通道宽度、上层通道宽度和下层通道高度为变量，以在泵功率等于1.2 W 时最小热阻为目标，变量及变量尺寸变动范围如表2 所示。

表2 散热器结构变量与变量尺寸变动范围

表2 中，uin为入口流速；Wc,u为下层通道宽度；Wc,l为上层通道宽度；Hc,u为下层通道高度。

为了便于计算，利用式（4）进行归一化，得到归一化的变量如表3 所示。

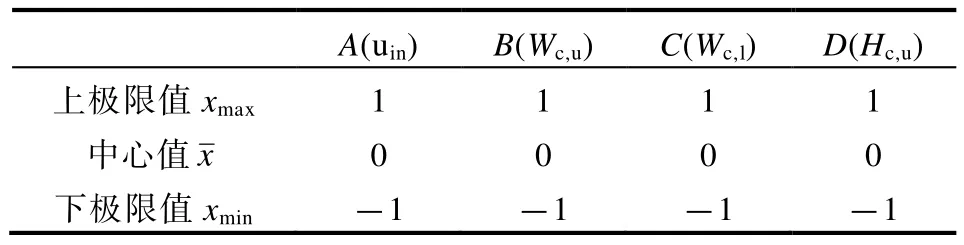
表3 变量与变量尺寸变动范围（归一化后）

式中，Z为归一化后的无量纲变量；Δx为设计变量取值范围的中心值即

中心复合设计是最常用的响应曲面法的试验设计方法，可以具体高效估计一阶和二阶项，从而评估因子的非线性影响。中心复合设计适用于多因素多水平实验，有连续变量存在的场景，中心复合设计能更好地拟合相应曲面。本研究利用中心复合法设计实验方案并得到结果，表4 列出了实验设计方案矩阵以及获得的热阻Rth和泵浦功率P结果。

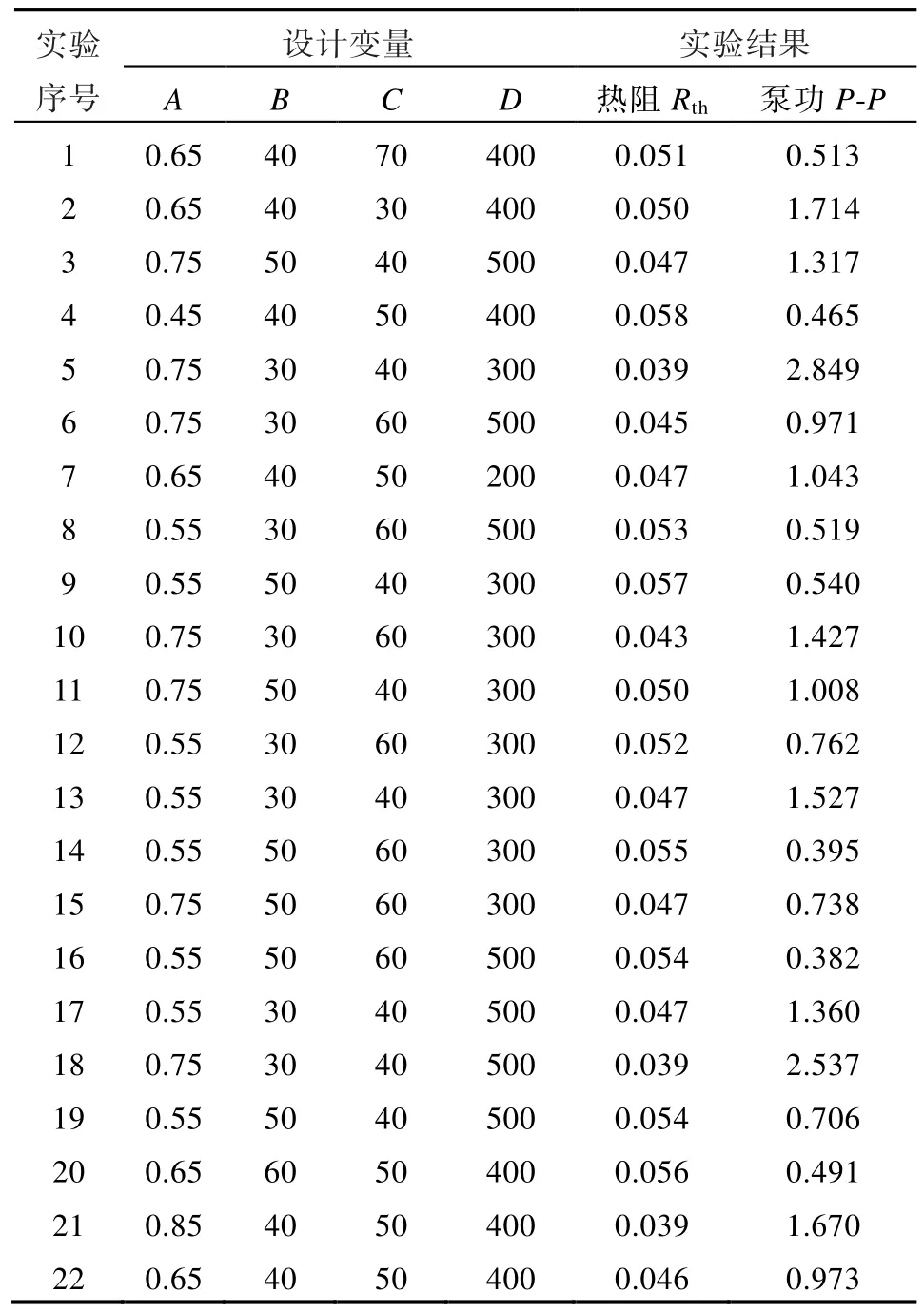
表4 实验设计矩阵和结果

表5 以方差分析的形式给出了热阻二次模型的结果。表5 中，“Model”项的P值为0.00，小于0.05（即a=0.01，或95%置信度时），这表明模型可信度高，可以认为具有统计意义，证明模型中的项对响应有显著影响。详细分析每一个模型项的影响，可以看出，因子A、因子B、因子C的主效应，二次项A×A、B×B、C×C以及因子B与因子C、因子B与因子D的交互效应是显著。尽管因子D的主效应不显著，但因子B与因子D的交互效应是显著，因此，拟合过程保留因子D的主效应项。因子C与因子D的交互效应F值小，P值趋近于0.05，因此忽略因子C与因子D的交互作用，其他项由于其P值大于0.05，可被视为不显著影响。

表5 热阻的方差分析表（不显著项消除前）

根据表5 的方差分析结果，删除D×D、A×B、A×C、A×D、C×D等不显著项，重新进行拟合，得到如表6 所示结果。表6 中“Model”的P值亦为0.00，证明模型具有显著的统计学意义，即模型中的各项对响应有显著影响。

表6 热阻的方差分析表（不显著项消除后）

由表6 可以得到热阻的二次回归方程：

同样的方法分析得到泵功二次回归方程：

本研究以泵功及空间大小为设计限制条件，对双层微通道散热器进行优化，目的是寻找最佳的设计约束值，根据上述分析最终形成优化的数学模型：

约束条件：

利用MATLAB 的fmincon 函数求解约束非线性规划，取整并经过逆归一化处理后得到双层微通道散热器的结构尺寸如表7 所示。

表7 优化后的新型散热器几何参数 单位：μm

4 结果与讨论

通过曲面响应法建立的回归方程显示了下层通道高度Hc,l、上层通道宽度Wc,u和下层通道宽度Wc,l三个因子对泵工和热阻的影响，可以看出，Hc,l主效应对热阻和泵工都不显著，而是与上层通道宽度之间有着显著的交互效应。Wc,u和Wc,l两个因子对响应影响显著，通过系数的正负可以很明显看出两个因子对热阻和泵工起着相反作用。对于泵工，Wc,u系数是Wc,l的四倍多；对于热阻，两者的系数差距不大。因此，通过减少Wc,u来降低热阻结合，增加Wc,l来控制泵工的方式来改善整体性能。图2 展示了优化后的散热器方案DMHSOP 在0.55 m/s、0.65 m/s、0.75 m/s、0.85 m/s、0.95 m/s和1.1 m/s 六个指定的入口速度时，泵功率与总热阻的关系，并与其他两种原尺寸DMHS-1、DMHS-2 做对比。可以看出，经过优化后，相同泵工时，热阻都有了下降，在泵工为1.2 W 时，与DMHS-1、DMHS-2 相比分布下降了9.42%、4.23%，证明了RSM 的有效性。

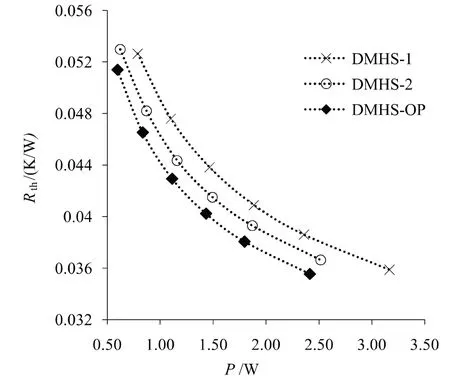
图2 泵功率与总热阻的关系对比

5 结论

本文对一种双层微通道散热器进行了优化研究，并与原始尺寸的双层微通道散热器进行了比较研究，针对响应和因子没有确切关系的情况，利用RSM 是一种比较合适的优化方法。通过RSM可以发现不同因子对响应的影响程度，同时可以看到不同因子间的交互效应。通过优化，改变上下层结构，增加下层鰭片厚度和通道宽度，可以逼迫更多流体流向下层通道，从而改善了流体的流动分布，整体性能得到进一步提升，比原始尺寸的双层微通道散热器热阻分别降低4.23%、9.42%。