一种基于场景的随机模型预测飞行策略
2023-05-08黄福全
黄 福 全
(北京飞机维修工程有限公司 四川 成都 610200)
0 引 言
随着科技发展,航空运输成为一种广泛热门的交通服务,在现代世界中起着十分重要的作用,它可以让人和商品快捷地到达遥远的目的地,提高了工作效率和降低时间成本。因此,航空运输已成为促进人民和社会之间经济和文化交流的重要手段。
为了确保飞机运作安全和工作效率,已开发了空中交通管理系统[1]。它们的目标是在提高成本效益的情况下,以管理和增加空域容量,并保证安全要求,预测和避免飞机飞行距离过近而发生的冲突。传统的空中交通管理系统结构严格:主要基于飞机必须遵循预定航线。空中交通预计将在未来几十年迅速增长,这种增长可能导致严格空中交通管理系统中航线饱和,且造成拥挤和延误。为了应付不断增加的空中交通,需要有新的方法来有效地利用空域,以确保飞机更有效率和更安全地飞行。
文献[2-3]提出的解决方案是基于4-D轨迹和目标窗口(目标窗口表示在给定的时间间隔内飞机需要通过三维空间的二维区域(通常是一个矩形)的4-D轨迹的约束条件)的方法。在SESAR[2]和CATS[3]项目中,航空公司、机场、航空导航服务供应商的新空中交通管理系统的关键技术是使用目标窗口。使用目标窗口将更有效地利用空域,提高飞机轨迹的可预测性,提高安全性和空域容量。
每架飞机都将被分配一系列的目标窗口,目标窗口的设计有两个目标:更好地利用空域容量和避免冲突。然而,目标窗口的应对并不简单,因为目标窗口在时空域中对飞机运动施加了约束,同时明确地考虑到飞机速度和加速度的物理限制,以及与乘客舒适度相关的其他约束。此外,飞机运动受到不确定性的影响,特别是风的存在,这导致飞机轨迹的不可预测性[4-6]。
本文的主要目标是开发一种运动控制方法能够引导飞机尽可能地接近参考轨道,实际飞行轨迹也能满足目标窗口的要求。
由于模型预测控制(Model Predictive Control,MPC)方法能够处理输入和状态变量约束,因此已有文献采用MPC方法在不受风扰动影响的情况下进行控制设计[7-8]。每个采样时刻,MPC在满足飞机的物理限制和乘客舒适度要求下最小化有限视界成本,以加强轨迹跟踪。所获得的控制作用仅应用于当前时刻,并在每个采样时间重复该过程。
在构造有限时域约束优化问题时,实现可计算性和可解性的一个关键问题是将原问题转化为凸优化问题。因此,需要针对飞机动力学模型为非线性的情况,采用反馈线性化的方法,得到一个具有新的输入变量和状态变量的线性模型,使其动力学特性与原模型完全匹配。然后将得到的线性模型进行离散化处理,从而嵌入到MPC控制器中。使用反馈线性化方法已经在文献[9-10]中被采用,而文献[10]从一般的角度讨论这一问题,其贡献是应用这种方法来解决一个飞机飞行控制问题。
目标窗口规范通常涉及到大的时间尺度和空间尺度,因此在MPC中每个时间步长中需要求解一个有限视界问题是困难的。因此,为了满足目标窗口规范,利用参考轨迹来满足目标窗口要求,同时计算飞机的运动能力。为了实现跟踪参考轨迹的目标,优化问题中加入了飞机位置约束。这些约束依赖于风扰动,这使得问题更具有挑战性,由于风扰动与飞机位置非线性相关,且风扰动具有无界支撑,这一事实阻碍了问题的可行性。
对于风扰动与飞机位置非线性相关的解决方法是将原始的风扰动模型替换为飞机当前位置的局部近似,该局部近似的飞机沿MPC的沿着预测视线飞进的空域区域内是准确的。对于风扰动具有无界支撑,考虑机会约束,以避免不可行性问题,从而产生一个机会约束优化问题。
为了处理机会约束问题,提出了一种基于采样的随机模型预测控制方法,它允许在低计算量的情况下找到机会约束优化问题的近似解。这样,最终将得到一个优化问题,可以有效地解决在每一个时间步长最优控制输入,且对风的扰动有较强的鲁棒性。
1 飞机动力学模型
1.1 飞机模型
为了简化飞机动力学方程,假设飞机为质量均匀分布对称的刚体,地球简化为平面大地[12]。飞机的位置在笛卡尔坐标中表示为x、y、z,飞机飞行对周围的空气的速度为V,偏航角为ψ(飞机速度的投影在x-y平面与x轴的夹角)和飞机的质量为m。系统的输入是俯仰角γ(即速度与x-y平面之间的夹角)和滚动角φ(即升力与包含飞机速度和z轴的平面之间的夹角),发动机的推力为T。风扰动添加在x、y、z轴上的分速度,这些扰动表示为wx、wy、wz。根据文献[11]中的式(1),简化的飞机动力学模型可写为:

(1)
式中:CD和CL为阻力系数和升力系数;ρ是海拔为z的密度函数;S为飞机的翅膀面积;g为重力加速度;η为燃料消耗速度。根据文献[12],升力系数设为:
(2)
(3)
最后飞机的动力学模型可写为:

(4)

1.2 飞行约束条件
为了考虑飞机的物理限制、乘客的舒适和安全要求,必须考虑以下状态变量和输入变量的约束。
(1) 飞机的真空速度为V:
Vmin≤V≤Vmax
(5)
式中:Vmin和Vmax取决于飞机类型,Vmin也与飞机失速速度有关[13]。
(2) 速度的加速度:
(6)
式中:aL=2 ft/s2=2×0.304 8 m/s2。
(3) 发动机推力:
Tmin≤T≤Tmax
(7)
式中:Tmin和Tmax可以根据文献[12]计算,也依赖于大气条件和飞机类型。
(4) 滚动角φ:

(8)

(5) 俯仰角γ:
γmin≤γ≤γmax
(9)
飞机的一些约束参数依赖于大气条件(压力、高度和温度)和飞行阶段(爬升、巡航和着陆)。然而,为了简化模型,假设这些参数已知。此外,在位姿控制问题中,它们可以被认为是常数,并且可以根据飞机当前的状态,在每一个时间步上根据位姿策略进行调整。
2 反馈线性化和约束重构
本小节将反馈线性化方法应用于飞机运动模型式(4),在一组新的输入变量和状态变量中得到与原始飞机动力学精确匹配的线性模型。通过一些变量的改变,将第1.2节中飞机物理限制和乘客舒适度的约束表示为新状态和输入变量的函数,结果证明该约束是非凸的。为了有效计算约束,引入凸逼近方法。
2.1 反馈线性化
本小节中,对系统式(4)进行反馈线性化,从而得到具有新的输入变量和状态变量的飞机线性模型。本方法受到了文献[13-14]的启发,其中考虑了一个更简单的二维空域的飞机模型。首先,对方程式(4)进行简化,忽略质量动力学,以便在应用MPC将质量视为沿时间视界的常量。二维空域的飞机模型可写为:
T=KDV2+mgsinγ+mτ
(10)
φ=tanφ
(11)
(12)
则控制系统演化的方程为:
(13)
新的控制输入为:
(14)
(15)
(16)
结合式(14)和式(15),可求出τ和φ:
(17)
(18)
τ=u1cosψcosγ+u2sinψcosγ+u3sinγ
(19)
联立式(10)、式(11)和式(18)有:
T=KDV2+mgsinγ+mτ
(20)
(21)
(22)
式(20)-式(22)定义的非线性反馈使得状态x1、x2、x3、x4、x5、x6关于新的输入u1、u2、u3线性相关:
(23)
新的状态和输入变量具有精确的物理意义,状态由飞机在笛卡尔坐标中的位置和速度组成。输入u1、u2、u3分别是沿x、y、z轴的加速度。此外,可以从新的状态变量中恢复原始状态变量,如下所示:
式中:atan(·,·)表示其参数的四象限反正切。
为了方便模型预测控制的后续开发,式(23)将被离散化,采样时间为Ts,则离散系统可写为:
(24)
式(24)可写为:
xk+1=Axk+Buk+Bwwk
(25)
2.2 在新的变量中重新表达约束条件
在2.1节中进行的反馈线性设计使将飞机模型式(4)重写为线性系统式(25),这无疑为MPC设计提供了条件。另一方面,用新的状态变量x1、x2、x3、x4、x5、x6和输入变量u1、u2、u3来重写状态约束和输入约束。本节考虑到MPC的后续应用,将在有限视界上重新构造约束,并在必要时引入适当的松弛来凸化它们。而引入松弛使初始约束至少在当前时刻被满足。
1) 飞机的真空速度为V:

(26)
(27)
根据文献[12]可将式(26)和式(27)写为:
其中:
-aL≤cosγk(u1,k+icosψk+u2,k+isinψk+
u3,k+itanψk)≤aLi=0,…,M-1
(28)
3) 发动机推力:
Tmin≤mcosγk(u1,k+icosψk+u2,k+isinψk+u3,k+itanγk)+
(29)
4) 滚动角φ:

(30)
5) 俯仰角γ:
由于x6=Vsinγ,得到:
Vksinγmin≤x6,k+i≤Vksinγmax
(31)
3 算法设计
本节将提出一种随机模型预测控制算法运用到飞机运行控制系统中。
3.1 飞机的控制问题陈述
为了控制飞机的动力学方程,在文献[15]提出方法的基础上进行修改。修改这个初始框架,以获得一个灵活的仍然相同属性的参考跟踪算法。rk+i表示飞行器需要跟踪的参考轨迹和速度。有限属于优化随机模型预测控制问题的代价函数J定义为两项的和:一项仅依赖油耗即输入uk+i,另一项考虑位置误差阈值,即代价函数可写为:
J(xk,uk,…,k+M-1)=
(32)
式中:Q≻0,R≻0,QM≻0。由于新状态受风扰动的影响,其约束难以得到满足。因此,假设在每个k时刻,系统状态服从以下机会约束:
P{xk+i|k∈Fx}≥1-εi=1,2,…,M
(33)
式中:Fx={x|Fx≤f}∈R6是一个多面体和F∈Rm×6,f∈Rm为约束式(26)、式(27)和式(31)对应的系数。ε∈[0,1]为预先确定的最大机会约束违反概率。与确定性约束不同,机会约束允许部分违反,这有助于缓解当干扰是无限时硬约束的不可行性的情况。同时施加硬输入约束:
uk+i-1∈Fu={u|Gu≤g}⊆R3i=1,2,…,M
(34)
式中:G∈Rm×3,f∈Rm为式(28)、式(29)和式(30)对应的系数。
给定预测时域M,系统式(25)的预测状态可以用如下形式描述:
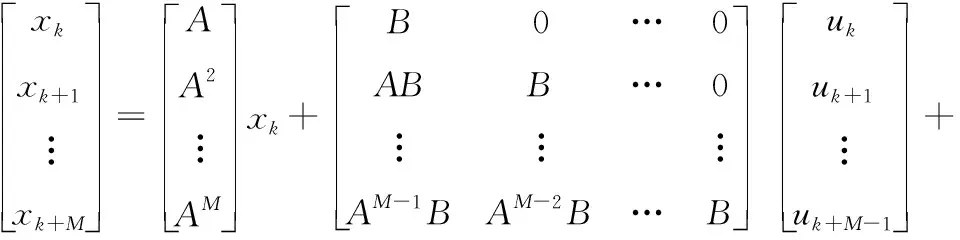
该式可以简化表示为:
x=Axk+Bu+Bww
(35)
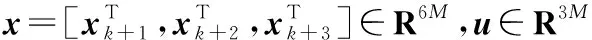
P{Fk+ix≤fi}≥1-εi=1,2,…,M
(36)
Gu≤g
(37)
式中:Fk+i和fi代表F=IM⊗F和f=1M⊗f的第i块向量,G=I3⊗G和g=13⊗g。式(37)与系统状态xk不同,操作变量uk在实际中总是受到执行器的限制,因此使用硬约束具有现实合理性。
给定2.1节的离散时间模型式(25)、3.1节讨论的约束转化为机会约束以及代价函数式(32),该飞机的控制有限时域优化问题如下:
(38)
s.t. 式(25)、式(36)、式(37)
计算得到的控制动作的第一个元素uk,作用于系统式(25),重复优化式(38),得到MPC控制。然而问题式(38)是很难解决的,因为存在机会约束这使得它是非凸的。
3.2 扰动反馈策略
使用一种普遍的干扰反馈扰动策略[16-17]:
(39)
式中:矩阵Mk,j和vk成为了原问题的决策变量。该仿射扰动策略类似于多阶段自适应鲁棒优化[18]中的仿射决策规则。将各阶段的反馈策略作为一个整体考虑,式(39)可以进一步表示为:
u=v+Mw
(40)
式中:M、v的具体形式与推导过程可参考文献[19],但是由于扰动wk具有无界支持,则系统输入将无界,从而不可避免地导致违反硬约束式(37)。为了解决这个问题,文献[20]制定了一个饱和的干扰反馈策略:
u=v+Mφ(w)
(41)
式中:φ(w)=[φ(wk),φ(wk+1),…,φ(wk+M-1)]和φ(·)是一个满足|φ(·)|≤1的饱和函数。在饱和的扰动反馈下,输入约束式(37)可以以鲁棒的方式[21]执行:
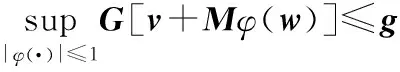
(42)
状态方程(35)在控制输入式(41)的作用下可写为:
x=Axk+BMφ(w)+Bv+Bww
(43)
同理,式(36)可写为:
P{Fk+i(Axk+BMφ(w)+Bv+Bww)≤fi}≥1-ε
(44)
假设E{φ(w)}=0,代价函数式(32)可写为:
J(M,v)=E{(x-r)TQ(x-r)+uTRu}=
vT(R+BTQB)v+tr{(R+BTQB)ME{φ(w)φ(w)T}MT}+
2vTBTQ(Axk-r)+2tr{MTBTQBwE{wφ(w)}}+C
(45)
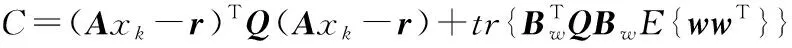
3.3 基于场景的近似


(46)
可以看出,问题式(46)是一个具有约束条件的确定性优化问题,可在软件包CVX中求解。由于干扰抽样的随机性,样本的数目对结果的有着重要的作用,文献[23]证明这一结果,因此可根据以下准则来选择采样干扰的个数Nt:
(47)
式中:dt为影响第t个机会约束的决策变量的数量;βt为预先指定的置信水平。因此,可以在概率意义上建立以下性能保证:
PD{P{Fk+i(Axk+BMφ(w)+Bv+Bww)≤fi}≥
1-ε}≥1-βt
(48)
式中:最外的概率项PD{·}来自于对多个场景采样的随机性,最内的概率P{·}与扰动序列w有关。保证式(48)是基于场景的随机模型预测控制问题的核心。
3.4 基于场景采样的随机模型预测控制算法
根据前文的叙述,可将飞机的轨迹跟踪问题描述如算法1所示。
算法1基于场景采样的随机模型预测控制算法
在k时刻,已知当前状态xk,寻找最优参数M,v
1.随机采样Nt个干扰数据;
2.输入:xk,ε;
3.输出:xk+1;
4.求解凸优化问题式(46);
5.将第四步求解的最优参数M*,v*作用于式(41)计算出u;
6.取出u中第一个元素uk作用于系统式(25)计算xk+1;
7.将xk+1作为当前时刻,返回到第2步进行循环计算。
4 仿真实验
在第2节的飞机模型和第3节开发的控制器进行了仿真。控制器需要操纵飞机沿着给定参考轨迹运行,且需满足物理限制和舒适性约束,并抵消风的干扰。为了测试控制器的性能,选择了一个有许多转弯和高度不变参考轨迹。
模型参数和约束边界的设置如表1所示。
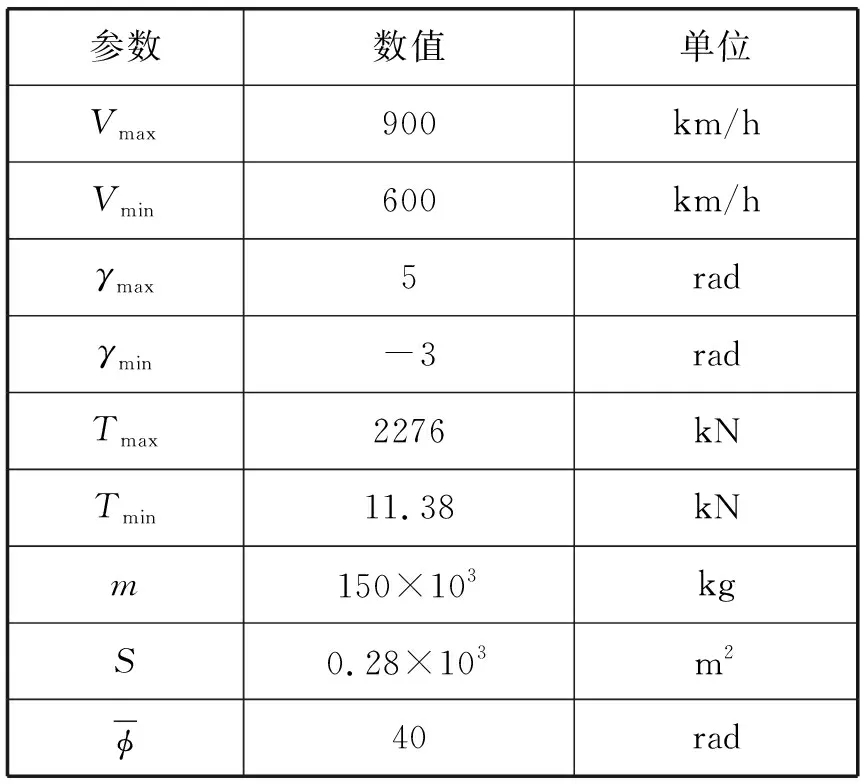
表1 飞机的参数
采样时间为Ts=5 s,初始位置和速度与参考轨迹的起始点和初始速度重合x0=[-40,0,3,601,601,0]T,有限预测时域为M=12,优化问题代价函数中的权重设置如下:Q=I6,R=0.02I3。机会约束的概率ε=0.1,基于场景的置信参数为βt=10-6,因此,根据式(47),相应的需要实现的干扰的数量为Nt=876。
参考轨迹的目标窗口集合如表2所示。

表2 目标窗口集合
假设设计的高度不发生变化,x-y参考轨迹如图1所示,从图1看出点6、7、8之间的路径几乎为一条直线,则可以在点6到7之间增加速度,如图2所示。同样的情况也发生在点4和点5之间,它们由一条直线连接。

图1 飞机位置参考轨迹图

图2 飞机设计速度V
根据本文提出的方法,仿真结果如图3-图9所示。从图3中可以看出,随机模型预测控制器能够操纵飞机,使其很好地跟踪图1中参考轨迹。飞机速度跟踪图如图4所示,可以看出,跟踪性能较好,且没有违反飞机运行速度的最小值和最大值。每个时刻飞机飞行的位置图如图5所示,在时刻170 s时,飞机位置在(0,0,4)附近,在时刻500 s时,飞机位置在(40,60,4)附近,在其他时刻也是满足表2设计的目标窗口集合。图6表示飞机在x、y、z轴方向飞行的速度图。图7展示飞机偏航角。图8为控制输入图,可以看出,控制输入没有违反约束,表明设计的饱和的干扰反馈策略是有效的。图9表达了飞机的俯仰角和滚转角,可以看出,本文方法满足设计约束,防止飞机转弯时速度过大造成乘客不舒适性,在风的干扰下实现了较好的稳定性。

图3 跟踪轨迹图

图4 速度跟踪图
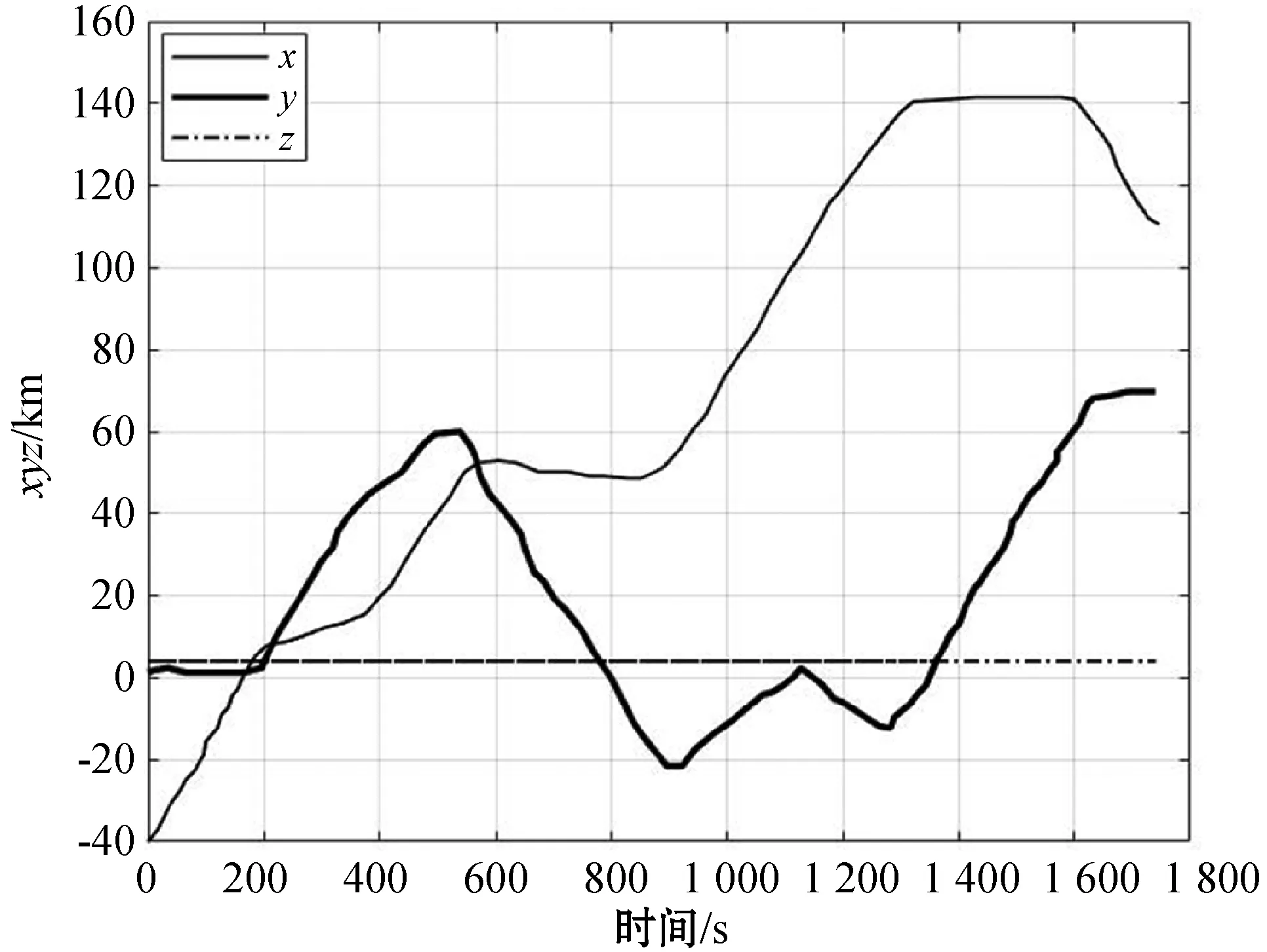
图5 飞机飞行位置图
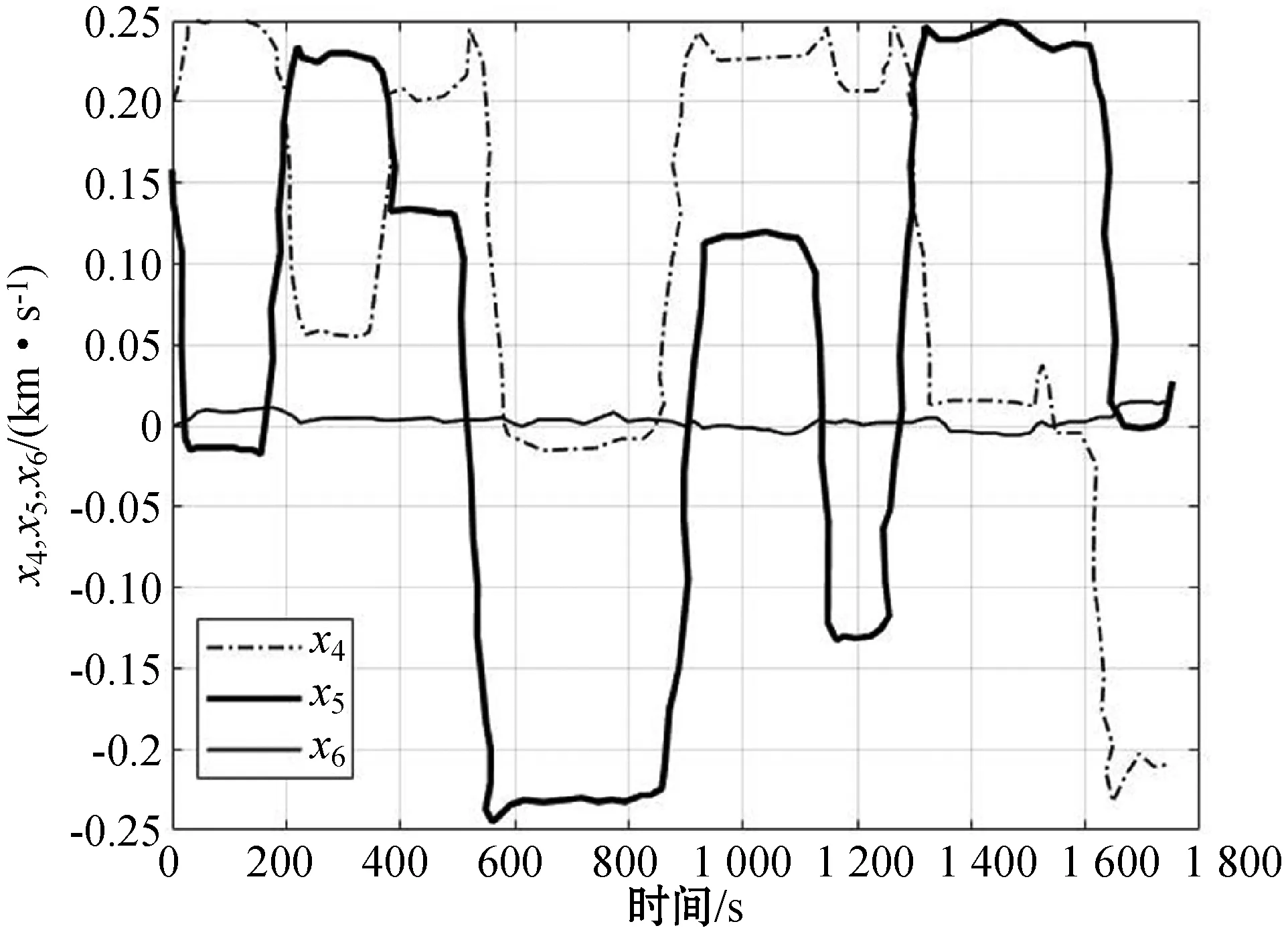
图6 飞机飞行速度图

图7 飞机的偏航角

图8 飞机控制输入图
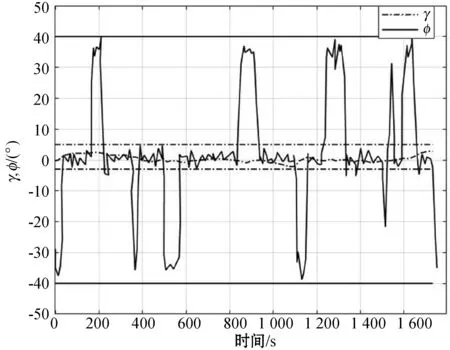
图9 飞机的俯仰角和滚动角
5 结 语
为了满足目标窗口对飞行器轨迹的时间和空间要求,本文针对非线性的飞机动力学模型性采用了反馈线性化的方法,得到一个与原模型完全匹配的新的输入变量和状态变量的线性模型。然后,将得到的线性模型进行离散化处理,从而嵌入到MPC控制器中。在MPC控制器的设计中,由于风的无界扰动,本文将约束设计为机会约束,并利用随机采样方法,将原问题转化为凸优化问题进行求解。仿真实验表明,所设计的用于飞行器运动的基于场景采样的随机模型预测控制器,在考虑飞机的物理限制和乘客舒适度约束的条件下,实现了对参考轨迹的跟踪,且对风扰动具有较强的鲁棒性。
