Dynamic crushing behaviors and enhanced energy absorption of bioinspired hierarchical honeycombs with different topologies

Xin-chun Zhng ,Nn-nn Liu ,Cho-cho An ,He-xing Wu ,N Li ,Ke-ming Ho

a Department of Mechanical Engineering,North China Electric Power University,Baoding,071003,China

b Hebei Key Laboratory of Electric Machinery Health Maintenance & Failure Prevention,North China Electric Power University,Baoding,071003,China

c School of Civil Engineering,Northeast Forestry University,Harbin,150040,China

d Department of Intelligent Engineering,Hebei Software Institute,Baoding,071000,China

Keywords:Bio-inspired honeycombs Crushing load uniformity Energy absorption Hierarchical topologies Finite element analysis

ABSTRACT In order to pursue good crushing load uniformity and enchance energy absorption efficiency of conventional honeycombs,a kind of bio-inspired hierarchical honeycomb model is proposed by mimicking the arched crab shell structures.Three bio-inspired hierarchical honeycombs (BHHs) with different topologies are designed by replacing each vertex of square honeycombs with smaller arc-shaped structures.The effects of hierarchical topologies and multi-material layout on in-plane dynamic crushings and absorbed-energy capacities of the BHHs are explored based on the explicit finite element (FE) analysis.Different deformation modes can be observed from the BHHs,which mainly depend upon hierarchical topologies and impact velocities.According to energy efficiency method and one-dimensional(1D)shock theory,calculation formulas of densification strains and plateau stresses for the BHHs are derived to characterize the dynamic bearing capacity,which is consistent well with FE results.Compared with conventional honeycombs,the crushing load efficiency and energy absorption capacity of the BHHs can be improved by changing the proper hierarchical topology and multi-material layout.These researches will provide theoretical guidance for innovative design and dynamic response performance controllability of honeycombs.

1.Introduction

Cellular solids have been widely used in many engineering applications of aerospace,automobile,packaging engineering,defence technology and so on due to their light weight and excellent performance ratio[1—5].With the further research on dynamic crushings and energy absorption capacities of cellular solids,the dynamic topological and hierarchical design have attracted great attention of the scholars at home and abroad[6—9].Therefore,how to explore the optimally hierarchical topology and then realize their controllable design of dynamic crushing performance according to engineering demands are one of important goals of sandwich structures and materials.

In recent years,hierarchical honeycombs have been developed based on conventional honeycombs with different topologies like triangle,square and hexagon [10—12].Many novel hierarchical structures with enhanced in-plane impact resistance and energy absorption capacities have been proposed by lots of researchers[11,13—15].And they indicated that introducing the hierarchy into conventional structures can effectively reduce the whole deformation of honeycombs.For example,based on the concept of hierarchical structures,An et al.[11]introduced self-similar hexagonal hierarchy at the vertex of cell structure to improve the dynamic strengths of honeycombs.Nian et al.[13]proposed an innovative self-similar graded honeycomb-filled thin-walled structure to systematically study the bending behaviors.They found that this kind of structure can present better energy absorption characteristics and crashworthiness performance than the corresponding uniform honeycomb-filled circular tube.Zhang et al.[14]obtained self-similar hierarchical circular tubes with higher average impact force and specific energy absorption by choosing suitable configurations.Lu et al.[15]proposed a novel hierarchical structure to effectively enhance energy absorption capacity of chiral structures.These studies reveal that mechanical behaviors of hierarchical honeycombs are affected by the low-order hierarchical structure and the order of hierarchical cell [16—18].Inspired by multi-level biological structure in nature,Xu et al.[16]constructed a self-similar layered hexagonal column with multi-order characteristics to improve the crashworthiness.Hou et al.[17]and Li et al.[18]developed self-similar multi-order hierarchical models to predict the dynamic response characteristics.Carrying out FE analysis on the dynamic collapse of self-similar hierarchical corrugated sandwich structures,Zhang et al.[19]found that the main deformation modes of collapse mechanism diagram and Euler buckling region of small compression bar will obviously change with increasing impact velocity.Du et al.[20]designed a novel hierarchical thermoplastic composite honeycomb cylindrical structures and experimentally investigated the mechanical response and energy absorption characteristics.Rahman et al.[21]combined hierarchical structure with cellular metamaterials to construct 2-order and 3-order positive Poisson's ratio hierarchy to explore the influence of defects on hierarchical structures.Kandasamy et al.[22]predicted the transient vibration behavior of hierarchical honeycomb plates with surface bonded actuators by controlling gain and hierarchical level.Although extensive researches on the mechanical properties and energy absorption capacities of hierarchical honeycombs have been carried out,most of them are directed toward the small deformation.Further research is needed to contribute to maintain good crushing load uniformity while enhancing in-plane energy absorption capacities of hierarchical honeycombs under large deformation.However,it should be pointed out that the maximum stress is mainly concentrated at the apex of conventional honeycomb where plastic hinge generates under in-plane impacts,which is not conducive to obtain good crushing load uniformity.Hence,how to select and design hierarchical topology is extremely important for the dynamic performance controllability of hierarchical honeycombs.

When subjected to impact loadings,the bio-inspired honeycombs based on structural bionics can absorb more energy due to their excellent impact resistance,which has the potential engineering application for the large-scale manufacturing of energyabsorbing structure protection and attracts a great deal of attention.With the development of bionic technology,many novel biomorphic honeycombs have been designed based on structural bionics aiming to improve the mechanical properties and enhance energy absorption capacities of conventional honeycombs[23—28].Xiang et al.[23]designed a new bio-inspired multi-layered structure which can effectively enhance energy absorption and crashworthiness by imitating the structure characteristics of human skeleton.Inspired by the shape of tortoise shell,Zhang et al.[24]proposed a bio-inspired re-entrant arc-shaped honeycomb to improve the absorbed-energy abilities of honeycombs.These results show that good crushing load uniformity is given in bioinspired honeycombs compared with traditional concave ones under in-plane impacts.On the basis of the concept of bionic design,Yang et al.[25]devised a series of bidirectional corrugated plates and revealed that impact resistance of corrugated structure can be effectively improved by reasonably drafting wave amplitude and wavelength.Ma et al.[26]constructed a biological materials with horseshoe microstructures to tailor its mechanical responses.Ha et al.[27]developed a bio-inspired sandwich wavy panel by imitating a woodpecker's beak,which expressed superior specific energy absorption than conventional sandwich panel.Ufodike et al.[28]proposed a bamboo biomorphic structure for in-plane energy absorption improvement and they indicated that the bio-inspired design showed significantly higher densification strain.Although bionic structure has good crashworthiness,the researches on the dynamic dominant mechanism and crushing performance adjustable design of the macro-/micro-structure with bio-inspired cellular materials under large deformation are far from enough.

Based on the inspiration of arched crab shell structures with surpassing impact resistance,three BHHs with different topologies are designed by replacing each vertex of regular square honeycombs(RSHs)with smaller arc-shaped structures in this paper.The effects of hierarchical topologies and multi-material configuration on in-plane dynamic responses and energy absorption capacities of the BHHs are numerically discussed.A comparative study between the BHHs and RSHs are carried out.Empirical formulas of densification strains and plateau stresses to characterize the dynamic properties are derived.Lastly,energy absorption efficiencies of the BHHs with different topologies and material configuration parameters are also explored.

2.Methodologies and models

2.1.Geometric configuration

In the nature,natural organisms can provide many excellent mechanical properties and energy absorption capacities after a long period of natural selection,such as turtle shell [24],horseshoe pattern [26],the beaks of woodpeckers [27]and the crab chela structures[29].It is interesting that all these configurations have a common feature,that is,they have the similar arched structures.The arched structure of crab chela can sustain strong impact loadings while cutting objects,which can provide excellent impact resistance for crab chela.Inspired by the arched crab shell structures,a kind of BHH model is proposed in this paper.Fig.1 shows the detail design strategy and representative volume element for a bio-inspired honeycomb.As shown in Fig.2,three BHHs are designed by replacing the nodes of the RSHs (Fig.2(a)) with different arc-shaped hierarchical topologies: (a) the BHH with circle cell (BHH—C,Fig.2(b)): the nodes of RSHs are replaced by circular structures;(b)the BHH with diamond cell(BHH-D,Fig.2(c)):the nodes of the RSHs are replaced by diamond-shaped structures which arc-edge of the circle is folded along the side of inscribed square with the circle to form a concave quadrilateral and the apex of the quadrilateral is connected with the ligament;(c) the BHH with re-entrant structure (BHH-R,Fig.2(d)): rotating the concave quadrilateral 45°in Fig.2(c) and connecting the concave arched edge with the ligament.With the evolvement of metal 3D printing rapid prototyping technology,the preparation difficulty of the BHHs will be greatly reduced and the manufacture quality can be effectively controlled.

Unit cell geometries of regular and bio-inspired honeycombs are displayed in Fig.3,wherelis the half length of unit cell with a RSH,erefers to the ligament length,randtare respectively the radius of the arched cell wall and the ledge thickness.Both the ligament and the introduced hierarchical cell thickness remain the same.In the filling,the half cell length of hierarchical honeycomb is a constant withl=2.4 mm.The relationship betweenr,eandlcan be given as

Relative density is a key indicator to describe the mechanical behavior of honeycombs.According to the definition of cellular material theory(CMT)[30],the relative densities of the BHHs with different topologies can be formulated as

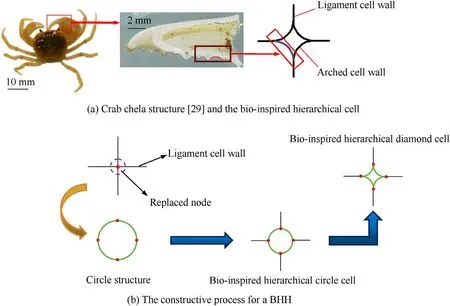
Fig.1.Design strategy and representative element for a BHH.

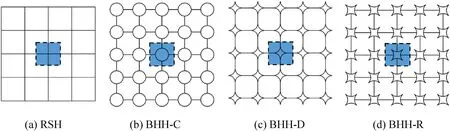
Fig.2.Cross-sectional geometries of regular and bio-inspired honeycombs.

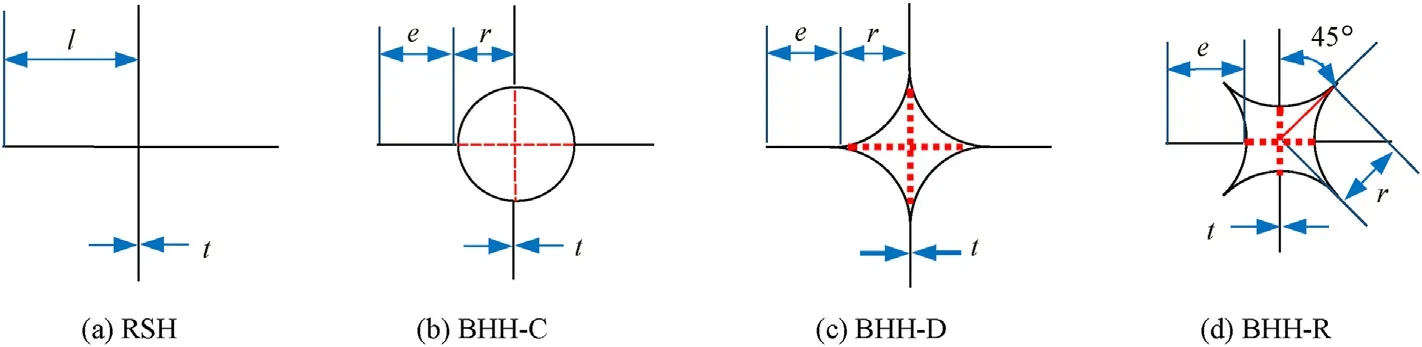
Fig.3.Unit cell geometries of regular and bio-inspired honeycombs.

where ΔρBHH-C,ΔρBHH-Dand ΔρBHH-Rare respectively the relative density of the BHH—C,BHH-D and BHH-R specimens,ρ* presents the density of the BHHs,and ρsindicates the density of matrix material.In particular,when the ligament length of cell wall with the BHH—C is 0,its relative density can be specified as

which is the same as the relative density of circular honeycomb[31].

2.2.FE models and the validation

In order to disclose the dynamic behaviors and energy absorption efficiencies of the BHHs,a FE model was established using ABAQUS/EXPLICIT.Fig.4 illustrates the diagrammatic sketches of the calculating model for the BHHs under in-plane crushing.The specimens are located between two rigid plates.The fixed rigid plate is on the bottom,and the impact rigid plate is crushing a specimen alongy-direction with a constant velocity [32,33].The matrix material are assumed to be elastic-perfectly plastic.The strain rate sensitivity is very low and ignored [12,24,32—34].To explore the effects of hierarchical topologies on dynamic crushing of the BHHs,the matrix material remains the same with typical aluminum alloy (Material-1) [34]and the corresponding material parameters are listed in Table 1.As for the multi-material layout models,the specimens are made of aluminum alloy [34]and aluminum (Al) (Material-2) [35],the material properties are also listed in Table 1.The materials of impact and fixed plates are assumed to be rigid.The width of the specimen isLxand the length isLy.Researches have shown that size effect on the dynamic response characteristics can be ignored when the number of filled cells is more than 5 [31—35].Here,the cell number is 13 in thexdirection and 14 in they-direction,which could effectively capture the dynamic mechanical behaviors.

Fig.4.Diagrammatic sketches of the calculating model for bio-inspired honeycombs.

Some researches have shown that shell element could ensure sufficiently reliable results[32—35].In this study,the specimens are also selected as shell element with S4R.The impact and fixed plates are employed by the discrete element with R3D4.For the consideration of convergence and calculation precision,five integration points are used along the thickness direction of each shell element.Mesh convergence analysises on element size are conducted firstly to test the validation of FE models.The best choice of meshing length is 0.21 mm for the BHHs according to the mesh convergence and computing efficiency conservatively.The out-of-plane displacement of FE model is limited during the crushing to prevent the out-of-plane buckling,and the specimen boundaries on the left and right edges are free.In this simulation,the fracture failure of matrix material was ignored.Moreover,automatic surface-to-surface contact was adopted to define the contact between the specimens and two rigid plates,and the friction coefficients were assumed to 0.2 [35].And general contact was defined for each surface of the specimen.The out-of-plane thickness of the BHHs was taken as unit thickness.To investigate the effects of hierarchical topologies,the BHHs can be obtained by changinge/l.Table 2 provides more details on the geometries and dimensions of the specimens.

Table 1 Matrix material parameters of the BHHs.

Table 2 Dimensions of the BHHs (unit: mm).

The validation of FE model was provided,the same model as in Ref.[31]was established to compare the dynamic response curve of a regular circular honeycomb.The nominal stress and strain of the specimens are respectively defined as

whereF(ΔLy) is the reaction force on impact rigid plate when the compression displacement alongy-direction is ΔLy,A0is the original cross-section area of the specimen before compression,bis the specimen thickness in out-of-plane displacement (in this paper,b=1 mm),LxandLyare respectively the width and the length of the specimen.At present,lots of researches on the dynamic responses of cellular structures have been explored based on FE simulation[10—12,24,31—35].It is proved that the FE modeling method is validated to be effective and accurate.Sun et al.[31]studied inplane crushing behavior and energy absorption performance of multi-layer regularly arranged circular honeycombs by using ANSYS/LS-DYNA.For the BHH—C specimen in this paper,whene=0,the model is the same with multi-layer regularly arranged circular honeycomb in Ref.[31].Fig.5 shows the dynamic response curve of a regular circular honeycomb atv=50 m/s.When matrix material,model size,impact velocity and boundary conditions are all the same,the nominal stress-strain curve of FE model in this paper is in good agreement with that of Ref.[31].But there is the difference between two curves at the beginning of impact.On the one hand,two different simulation products are exployed to investigate the dynamic responses.Two softwares will cause the error difference at the beginning of impact.On the other hand,more output datas are captured in our simulation to achieve higher calculation accuracy.It should be noted that both the trends and amplitudes between two curves at the beginning of impact are the same.It is seen that FE model established in this paper is reliable and the same method will be used to explore the dynamicbehaviors and absorbed-energy capacities of the BHHs with different topologies for subsequent study.

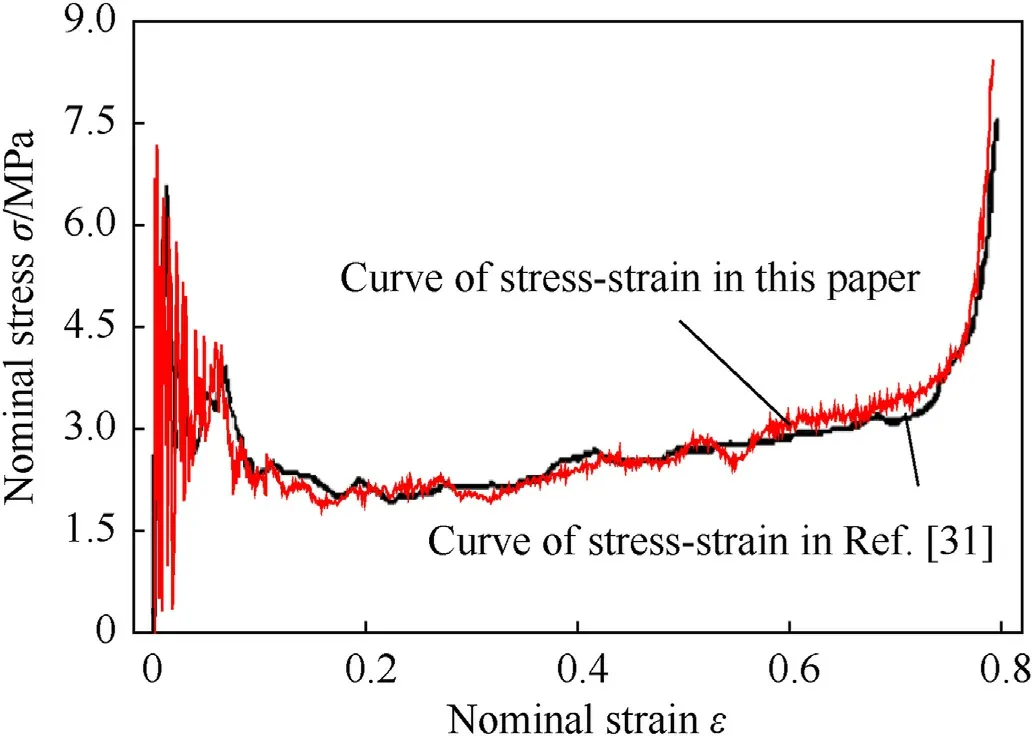
Fig.5.The nominal stress-strain curves for the BHH—C with e/l=0 at v=50 m/s.

2.3.Basic properties and evaluation indexes

Many researches indicated that impact velocity was an important factor affecting the dynamic response characteristics of cellular solids[32—38].Different stress waves are generated at the proximal end under different impact velocities.When impact velocity is higher than wave trapping velocity,local deformation of cellular solids will begin to occur.According to the ‘wave trapping’ theory[33],wave trapping velocity can be specified as the first critical velocity,which can be written as

where εcris initial strain of cellular solid when the crushing stress reaches initial peak stress,and σ′(ε) refers to elastic modulus in linear stage.For Δρ=0.115,the first critical velocity for the BHH—C,BHH-D and BHH-R specimens are estimated as 9.4,12.7 and 8.5 m/s,respectively.With the increase of impact velocity,the deformation gradually tends to be localized.Local collapse zone begins to propagate from the impact end to the fixed end in the form of shock waves.The critical velocity at which shock waves propagate in cellular solid is considered as the second critical velocity[32,37,38].

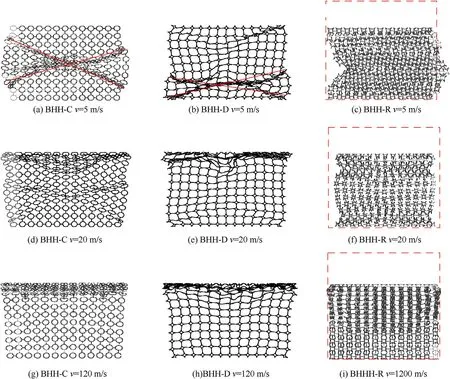
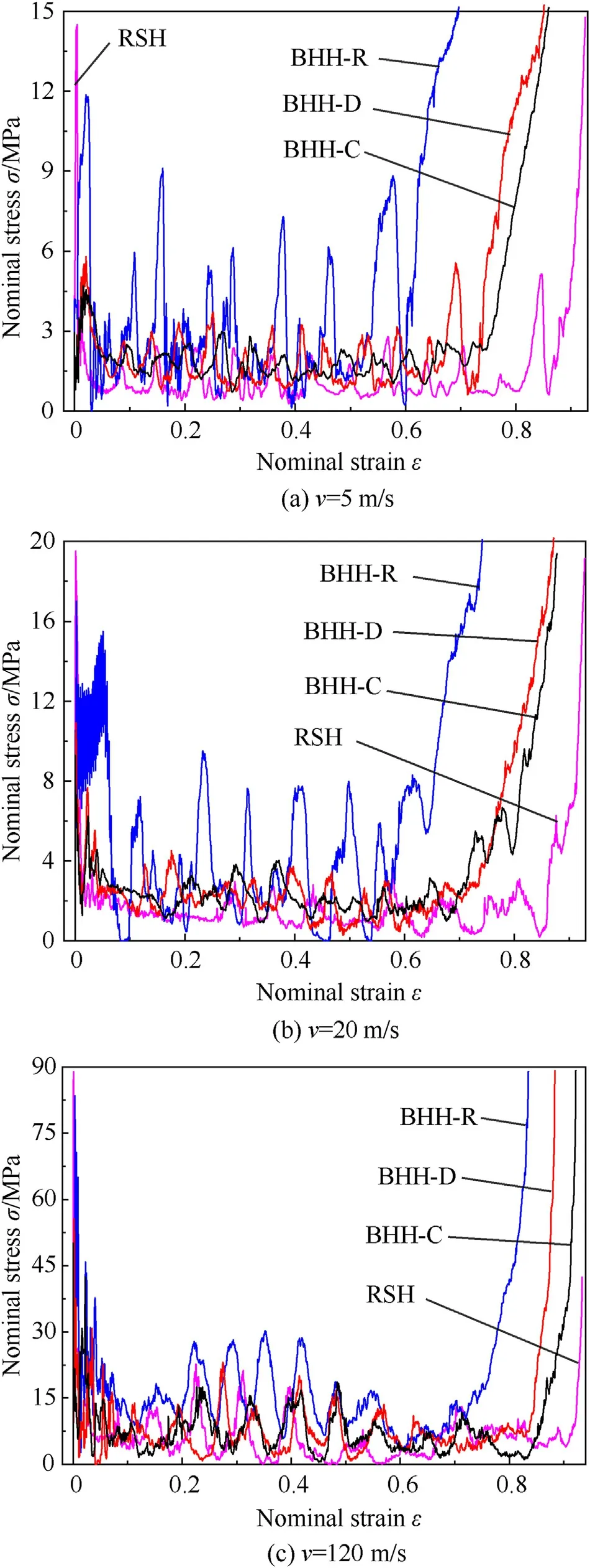
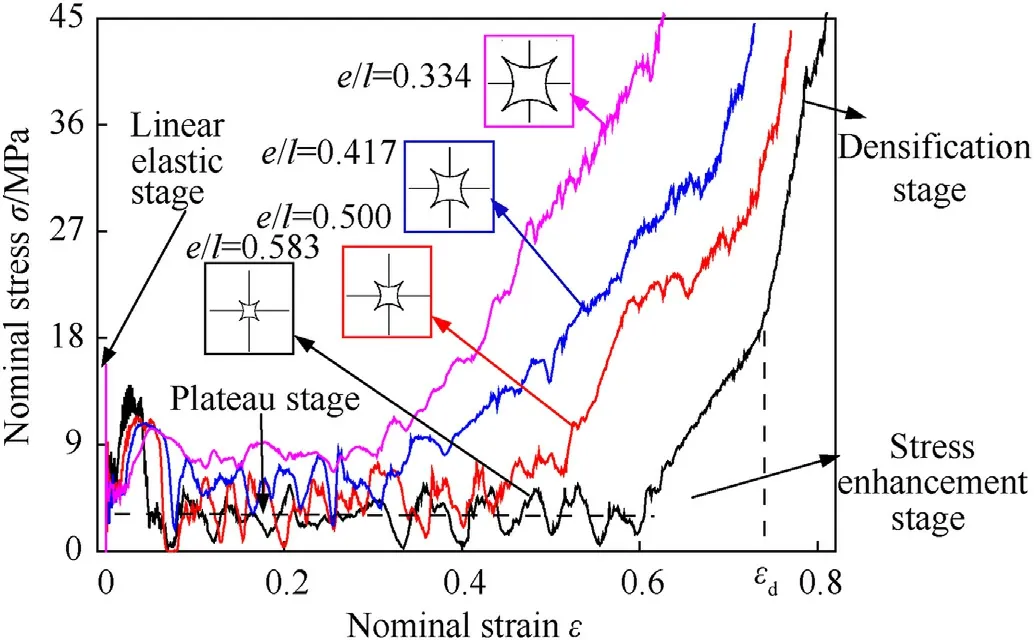
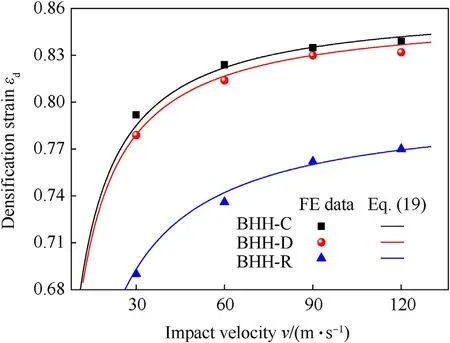
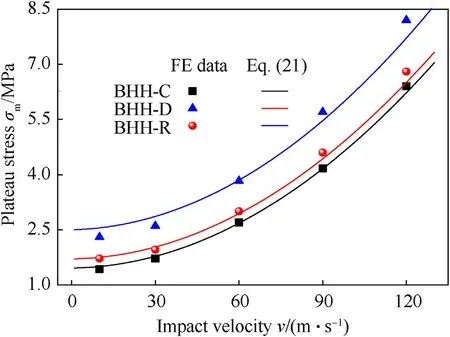
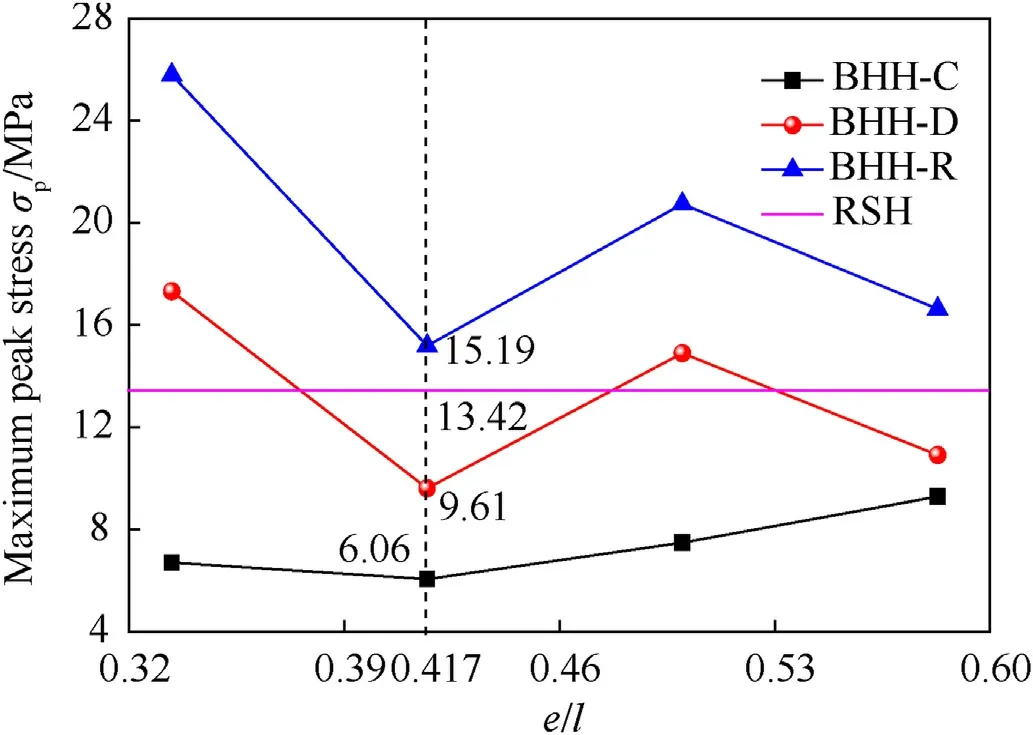
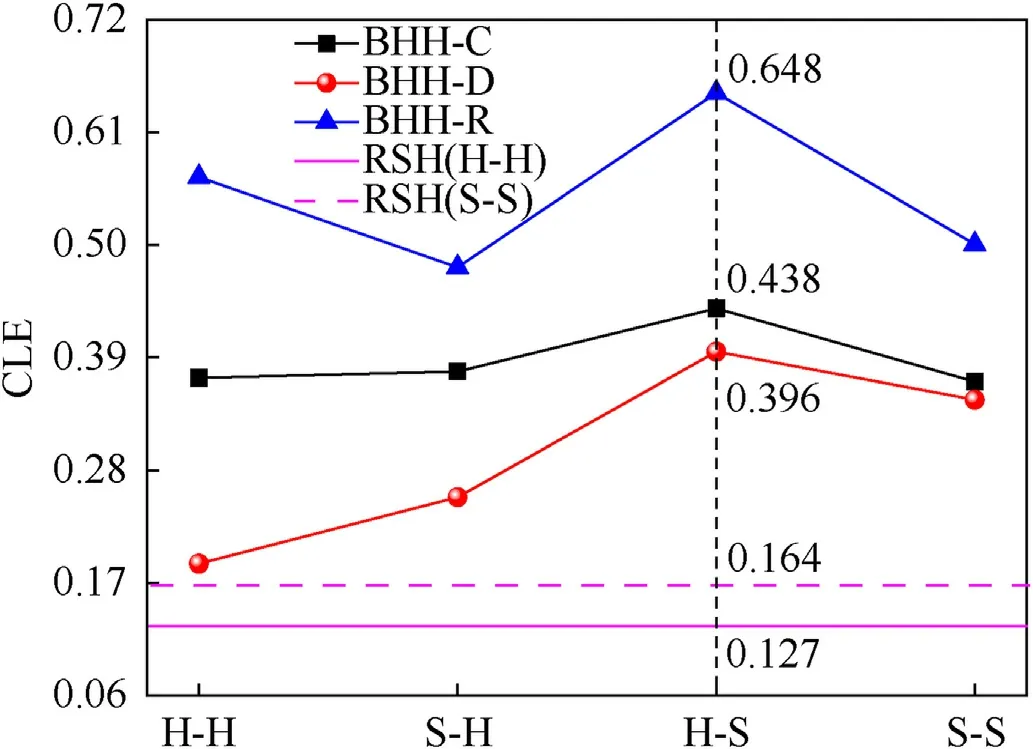
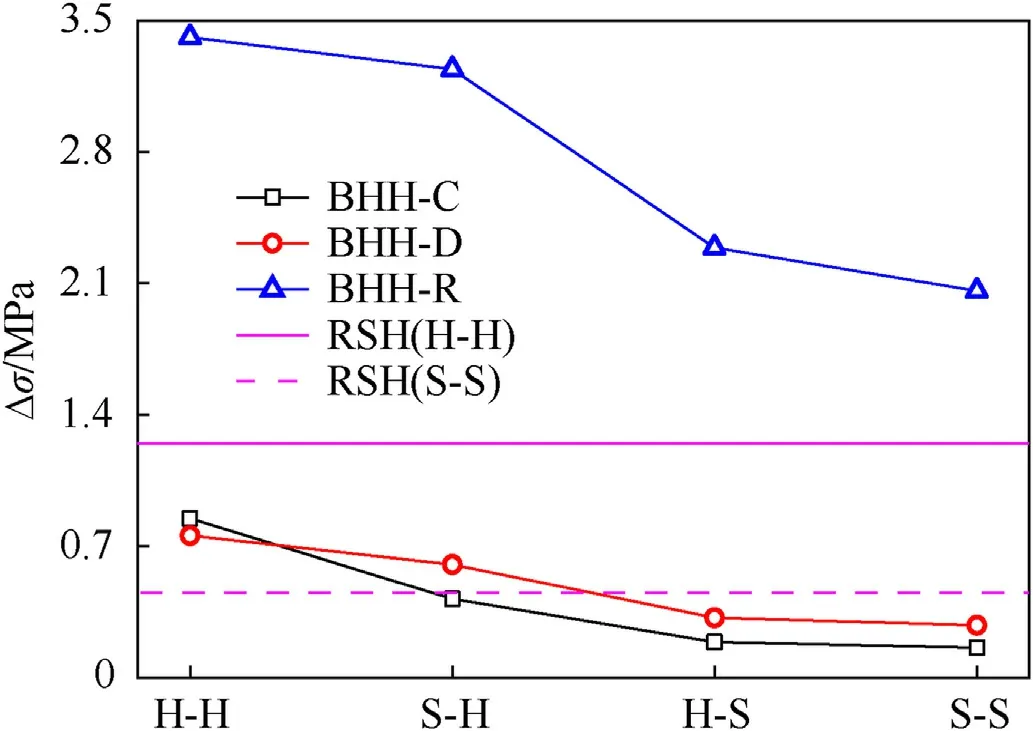
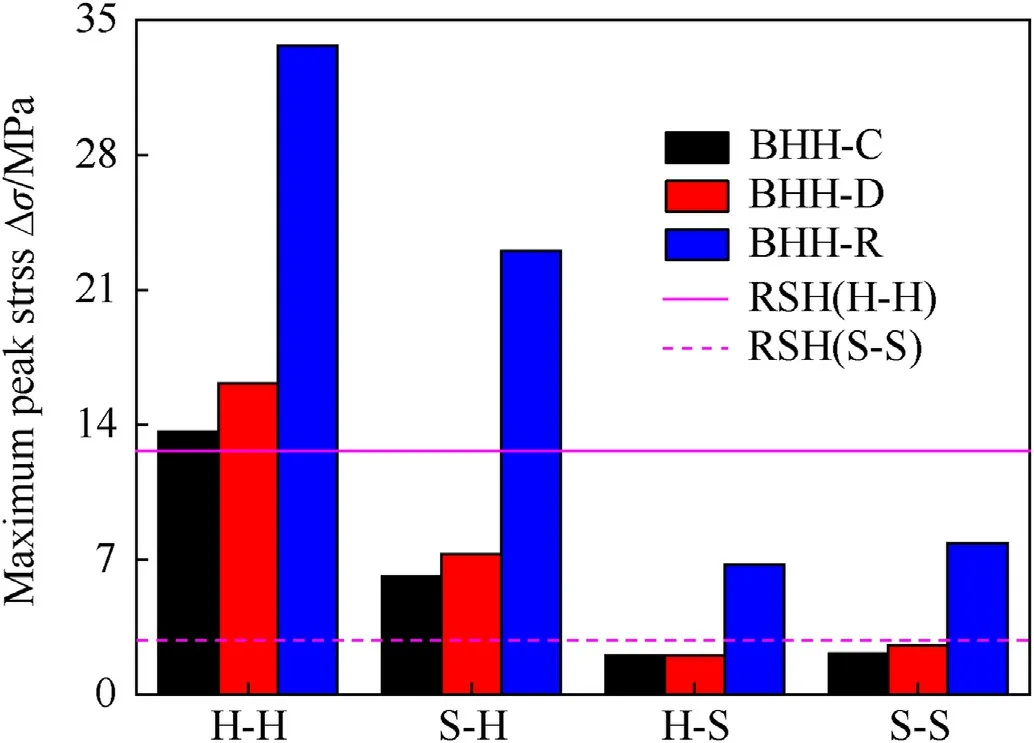
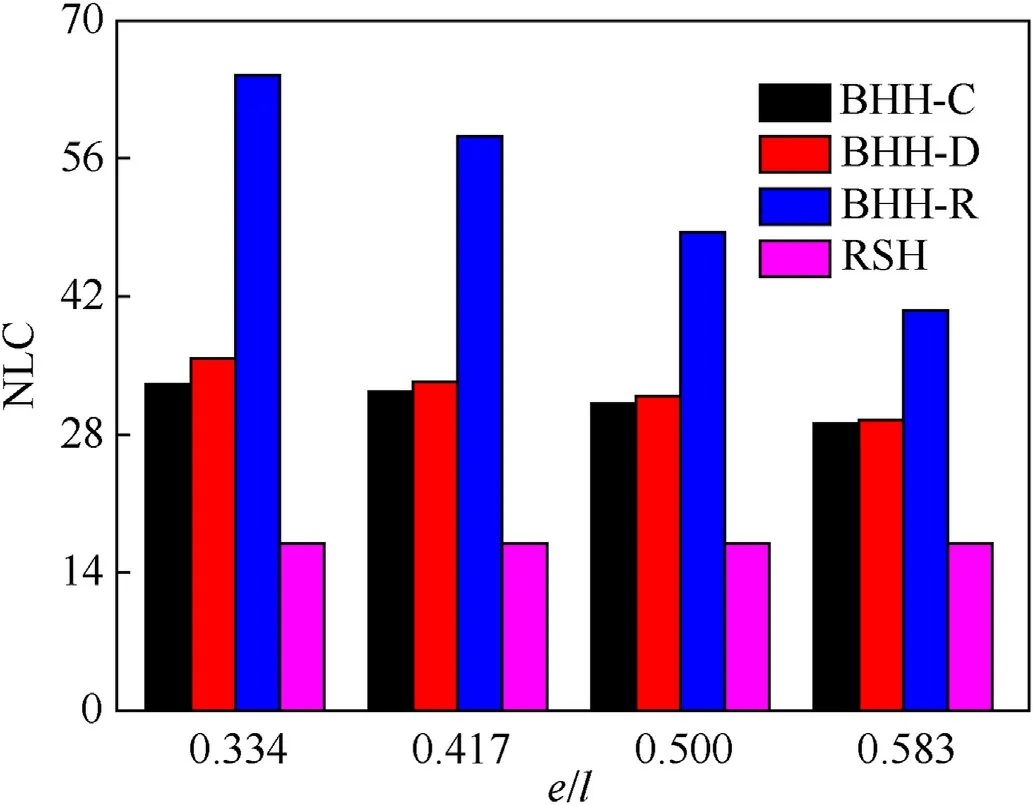
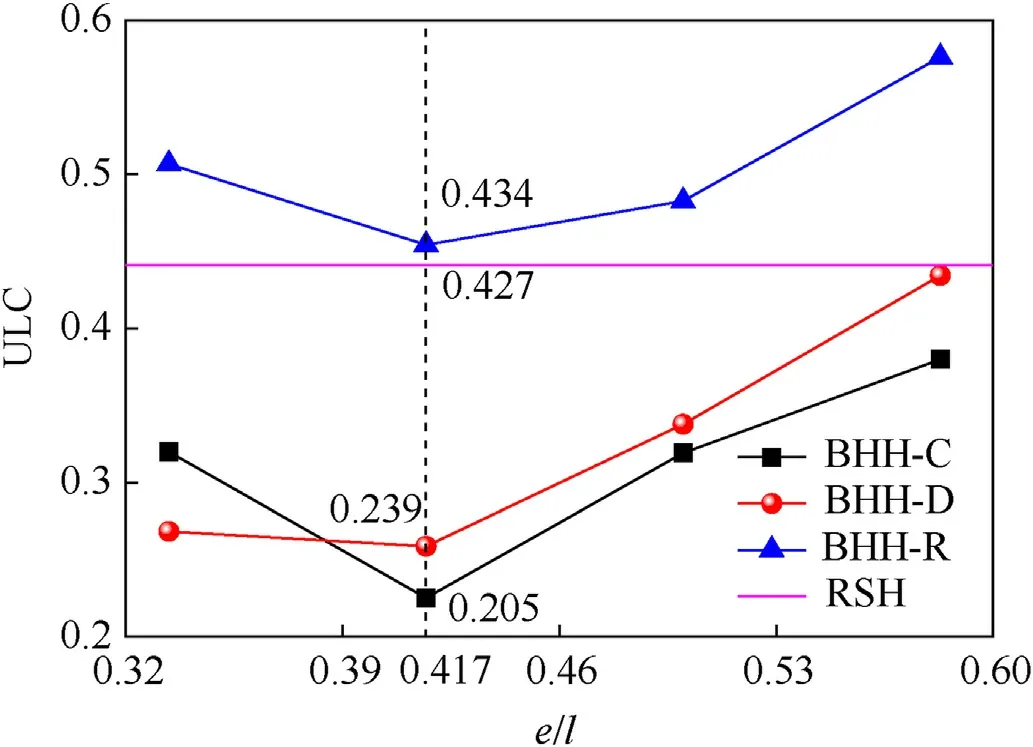
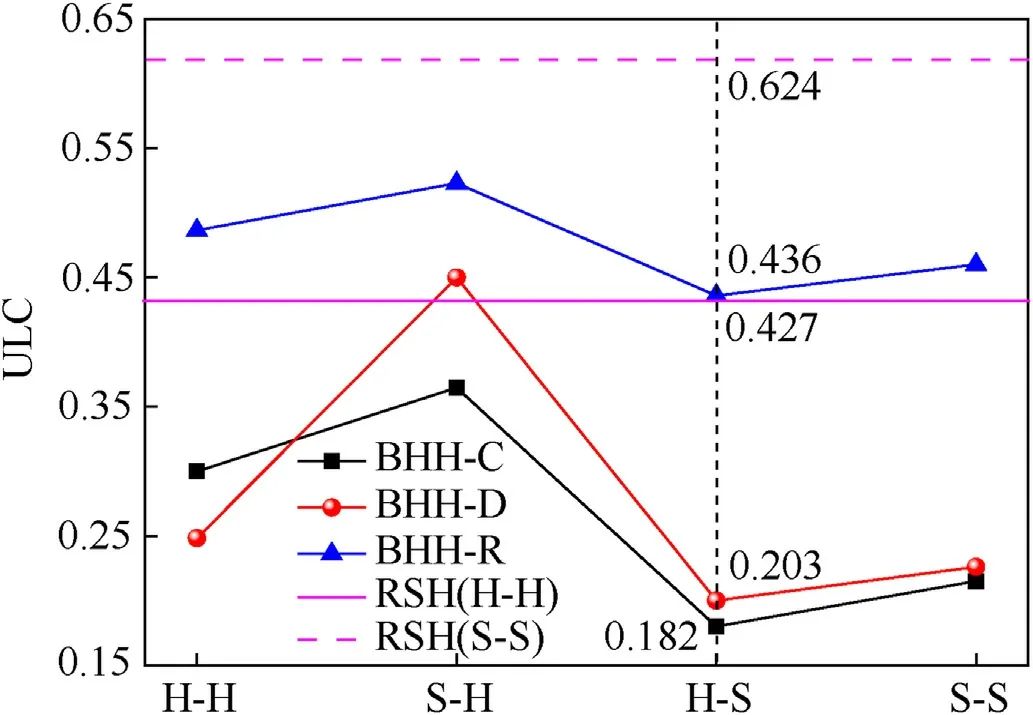
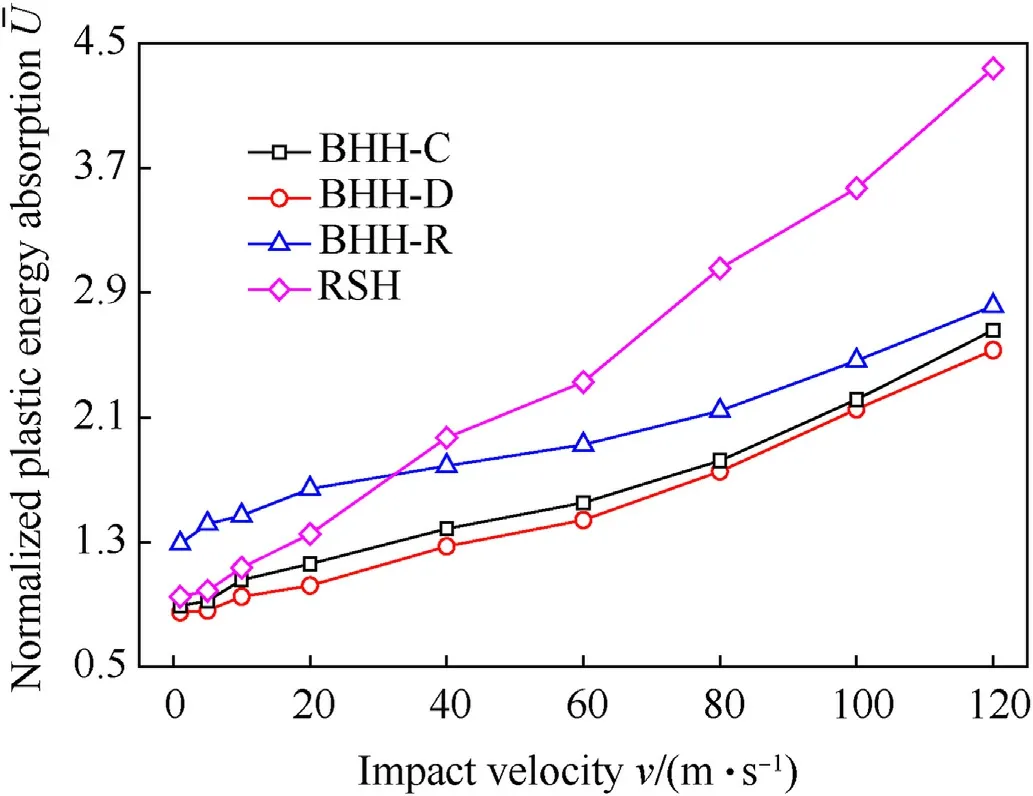
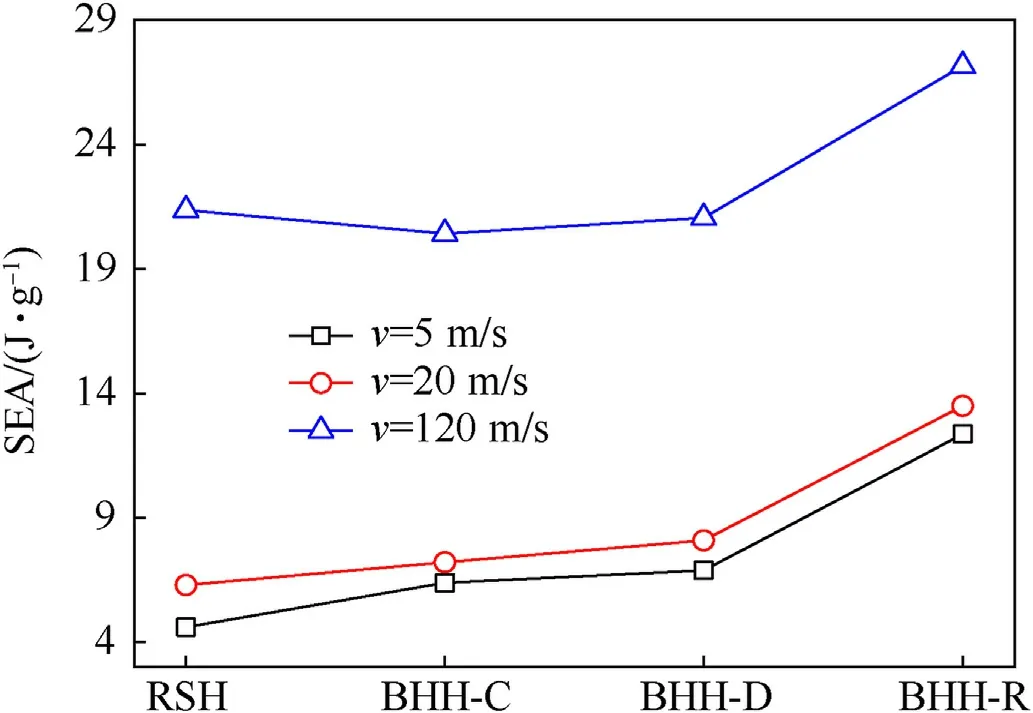
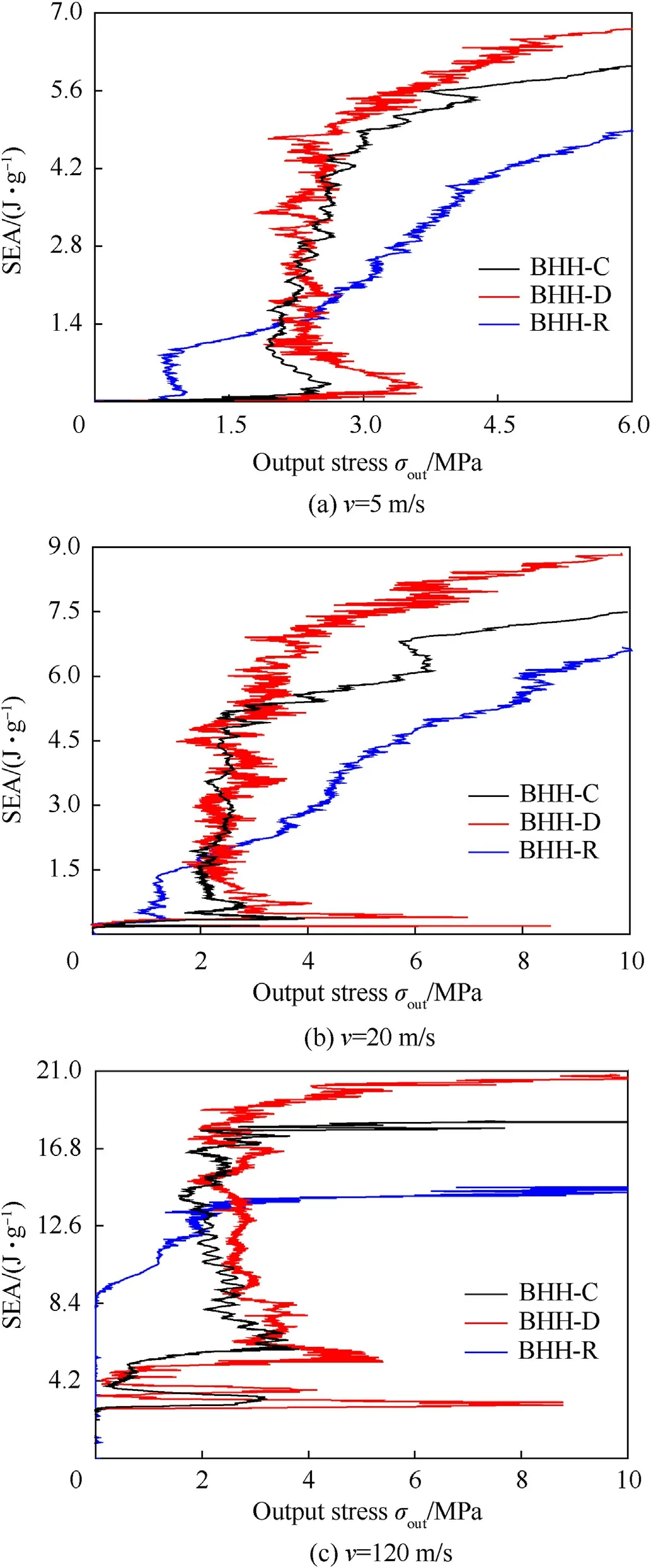
where σ0represents the quasi-static plateau stress and εdrefers to the densification strain.When Δρ=0.115,the second critical velocity for the BHH—C,BHH-D and BHH-R are 62.6,65.1 and 53.9 m/s,respectively.In order to explore the effect of impact velocity on dynamic behaviors,impact velocity ranges from 1 to 120 m/s.Based on the above definition of critical velocity,the range of impact velocity is divided into three sections.Whenv

Fig.6.Nominal stress-strain curve(black line),energy efficiency-strain curve(red line)and the corresponding specific energy absorption curve for a BHH.

Fig.6 shows the typical dynamic response curve(black line)of a BHH,which contains three stages: the elastic stage with the maximum peak stress σp,the plateau stage with the plateau stress σmand the compressed densification stage.σmis a significant index to describe energy absorption capacity of honeycombs,which can be obtained by

where εcris the initial strain corresponding to the peak stress.Our researches show that εcris greatly small during the crushing,a valure 0.02 is assumed for initial strain to ensure the higher calculation accuracy.εdis the densification strain.When the strain is over the densification strain,the stress of honeycombs will increase sharply.It is obvious that plateau stress is directly correlated to εd.The perfect densification strain is the porosity of a honeycomb,that is εd=1-Δρ.However,it should be mentioned that εddepends upon impact velocities and topological structures[32—35].In order to avoid the randomness of artificial selection,εdcan be obtained by using the energy efficiency method,which can be given as

whereEis energy absorption efficiency of a honeycomb,which can be defined by the ratio of the strain energy to corresponding nominal stress as

When honeycombs are used for energy-absorbing components,good crushing load uniformity should be maintained during energy dissipation.The maximum peak force should be lower than the critical one of destroying the protected components.Furthermore,in order to prevent the dynamic damage to the protected structure,the reaction force of honeycombs should be kept as constant as possible.There are many indexes to describe the crushing load uniformity of honeycombs [12,24],which can be given as

where CLE is the crushing load efficiency,σmis the plateau stress,Δσ refers to the average stress fluctuation and σpis the maximum peak stress in the dynamic response curve.For an ideal energy absorber,a smaller σpand a higher σmare needed.Due to σm≤σp,that is,0

Moreover,a non-dimensional indicator (NLC) is used to characterize the effective load-carrying capacity of honeycombs [39],which can be obtained by

whereFmis the average reaction force on the impact plate,M0is the fully plastic bending moment per unit length,which can be formulated as

in which σysis yield stress of matrix materials andtrepresents the edge thickness of honeycombs.Moreover,undulation of loadcarrying capacity (ULC) is another dimensionless indicator to reflect the undulation degree of impacting stress around plateau stress during the plateau stage,which can be defined as

where σmis plateau stress,εdis densification strain.

Due to the demands of lightweight structure design,the sensitivity of material weight should be considered in many energyabsorbing components.A specific energy absorption (SEA) is a crucial index to evaluate the energy absorption capacity of sandwich structures[24,33,35],which can be defined as

whereEVis the densification strain energy which can be determined by,Δρ is the relative density of the specimen and ρsis the density of matrix material.Furthermore,is also adopted to characterize the influence of impact velocity on energy absorption capacity [40].It normalizes the plastic energyU0by the perfect static plastic energy absorption,which can be defined as [41].

where σ0is the static plateau stress,A0andLyare the originally sectional area and length of the specimen,respectively.

3.Numerical results and discussion

3.1.Deformation characteristics

Many researches have shown that different collapsed modes are observed in honeycombs with different topologies under impacts.And the deformation mechanisms for hierarchical honeycombs depend upon cell micro-structures [11,12,15,24].In order to study the influences of hierarchical topologies and impact velocities on the deformation mechanisms of the BHHs,the deformation modes for the BHH—C,BHH-D and BHH-R with different impact velocities are discussed in this section.

Fig.7 displays the macro-scopic deformation of three BHHs at ε=0.35.For low-velocity crushing (v=5 m/s

3.2.Densification strain and plateau stress

Plateau stress (σm) and densification strain (εd) are two key indexes in describing the dynamic behaviors of honeycombs.Fig.10 shows the effects of impact velocities on the densification strains for the BHHs with different topologies.For the same hierarchical honeycombs,εdwill increase with impact velocity [35].It can be predicted by the following equation with impact velocity [12].

Fig.7.Deformation modes of the BHHs at ε=0.35 under different impact velocities.

where bothkandware constants,which depend on hierarchical topologies.The fitting values forkandwof the BHHs are obtained from energy efficiency method and FE results.Therefore,the empirical formulas of εdfor the BHHs with different topologies can be predicted as

According to the theory of 1D shock waves,Reid and Peng [42]proposed a simple formula of plateau stress for cellular solid,which is related to relative density and impact velocity

whereAis a parameter which can be decided by cell topologies of cellular solids.Gibson and Ashby indicated that Eq.(20)can also be applied to other cellular solids [29].Using the least square fitting method and introducing Eq.(19)into Eq.(20),the dynamic plateau stress at the impact end for the BHHs with different topologies are obtained,which can be written as

Fig.8.Nominal stress-strain curves of the BHHs with different velocities for e/l=0.583.

Fig.9.Nominal stress-strain curves of a BHH-R with different e/l at v=20 m/s.

Fig.10.Variation of densification strains for BHHs with respect to impact velocities.

Fig.11.Variation of plateau stresses for the BHHs with respect to impact velocities.

Fig.12.Δσ and CLE for the BHHs with different e/l at v=20 m/s.

3.3.Crushing load uniformity

As an excellent energy absorbing structure,the higher crushing load efficiency(CLE),and the lower average stress fluctuation(Δσ)and peak stress(σp)are required.Fig.12 illustrates the Δσ and CLE for the BHHs with differente/latv=20 m/s.For comparison,the corresponding results of the RSHs are also given.Obviously,the CLEs of the BHHs are higher than that of the RSHs.They first increase to the maximum value ate/l=0.417,and then follow a decline with the increasing ofe/l.The CLE of the BHH-R is the highest,which is 71.89%,164.76% and 521.26% higher than the BHH—C,BHH-D and RSH specimens,respectively.As shown in Figs.12 and 13,the mean stress fluctuation and maximum peak stresses of the BHHs could achieve the minimum value ate/l=0.417.For the BHH-R,σpis larger than that of other hierarchical honeycombs (as shown in Fig.13).The σpof the BHH—C is the lowest compared with other specimens for differente/l.This indicates that the crushing load uniformity of the BHHs can be improved by changing the propere/l.The BHH—C specimens are more suitable for energy absorbing components than other honeycombs when considering the crushing load uniformity under large deformation.

Fig.13.Variation of σp for the BHHs with different e/l at v=20 m/s.

Fig.14.CLE for the BHHs with multi-material configuration.

In order to explore the influence of multi-material configuration on crushing load uniformity of the BHHs,two kinds of matrix materials (as shown in Table 1) are considered to establish four layout models,which are the H—H,S—H,H—S and S—S,respectively.Take H—S model for example,S (Material-2) refers to matrix material of the introduced joint hierarchy,and H (Material-1) is the corresponding ligament material.Similarly,S—H indicates the material of the introduced joint hierarchy as Material-1.H—H and S—S define the same matrix material of the whole model as Material-1 and Material-2,respectively.Additionally,in order to compare multi-material configuration between the BHHs and RSHs,two materials are also considered in the RSHs,that is the RSH(H—H) and the RSH(S—S).

Whenv=20 m/s ande/l=0.334,the CLE,Δσ and σpfor the BHHs with different material layouts are shown in Figs.14—16.In contrast,the corresponding results of the RSHs are also given.It is clear that the BHHs with H—S configuration can obtain the higher CLE (as shown in Fig.14).Especially,the BHH-R with H—S has higher CLE than other hierarchical models,which is 48.07% and 63.91%higher than BHH—C and BHH-D,respectively.The CLE of the BHHs with multi-material layout is higher than that of the RSHs,as shown in Fig.14.However,the Δσ and σpof the BHH-R are always greater than those of BHH—C and BHH-D(Figs.15 and 16),which is mainly related to the deformation mechanism.Moreover,the BHH—C with multi-material configuration has the low stress fluctuation,which is even lower than the RSH with S—S.It can be observed from Fig.16 that σpof the BHHs with H—S are more advantageous for energy absorption than that of other layouts due to the lower peak stresses.Therefore,the BHHs with H—S perform well in all aspects for the crushing load uniformity.The reason is that due to the introduced joint hierarchy of low yield stress,the plastic deformation is first observed in introduced hierarchical structures and then the ligaments,which causes the whole deformation of the specimens.The BHH-R specimens exhibit excellent performance in CLE under large deformation,but they exhibit the higher Δσ and σp.It can be seen from the above analysis that compared with the RSHs,the crushing load uniformity of the BHHs can be improved if the proper multi-material layouts are chosen.

As an excellent energy absorbing component,the higher dynamic load-carrying capacity and smaller undulation of loadcarrying should be considered.Fig.17 shows the variation of the NLC for the BHHs with different topologies atv=20 m/s.The NLC of the BHH-R is obviously higher than that of the BHH—C,BHH-D and RSH specimens,which is consistent with Fig.12.However,for the BHH—C and BHH-D,the NLCs are relatively stable (they will fluctuate around 30)due to their insensitivity to the variation ofe/l.The NLC of the BHH-D is slightly higher than that of the BHH—C.It can be seen from Fig.17 that the NLCs of the BHHs are obviously higher than that of the RSHs.Research results show that the NLC of the BHHs can be improved and effectively controlled through the proper choice ofe/land the introduced hierarchical topologies.

Fig.15.Δσ for the BHHs with multi-material configuration.

Fig.16.σp for the BHHs with multi-material configuration.

Fig.18 shows the variation of ULCs for the BHHs with respect toe/latv=20 m/s.Along with the increase ofe/l,the ULCs of the BHHs will decrease first to the minimum ate/l=0.417,and then followed by an upward trend.The ULC of the BHH-R is higher than the RSH.It is seen that all BHHs can obtain better ULC ate/l=0.417,and the BHH—C has lower ULC than other specimens,which is 117.17%,108.29% and 16.59% lower than the RSH,BHH-R and BHH-D,respectively.Fig.19 shows the effects of multi-material layout on the ULC of the BHHs with different topologies.For the BHHs with H—S,the introduced joint hierarchy first deforms due to less yield stress,which prompts the whole deformation of the BHHs.It is the reason that the ULC of the BHHs with H—S can obtain the optimal value.Research results show that selecting the appropriatee/land using multi-material layout can decrease the undulation degree of impact stress for the BHHs.

Fig.17.Variation of NLC for BHHs with respect to e/l at v=20 m/s.

Fig.18.Variation of ULC for the BHHs with respect to e/l at v=20 m/s.

3.4.Energy absorption characteristics

Based on Eq.(17),the variation offor the BHHs with respect to impact velocity is shown in Fig.20.A higher value ofindicates that inertial effects have more significant enhancement on energy absorption of honeycombs.increases with the increase of impact velocity.The BHH-R has the higherthan the BHH—C and BHH-D.Under low-velocity impacting(v

Fig.19.ULC for the BHHs with multi-material configuration for e/l=0.334 at v=20 m/s.

Fig.20.Variation of for the BHHs with respect to impact velocity.

Based on Eq.(16) and energy absorption efficiency method,Fig.21 shows the effects of impact velocity on the SEA of the BHHs with the same cell-wall thickness.As a comparison,the SEA of the RSH is also given.With the increase of impact velocity,the SEAs of the BHHs are obviously improved.For the same impact velocity,the SEA of the BHH-R is higher than that of other hierarchical topologies and the RSH,which is consistent with dynamic load-carrying capacity(as shown in Fig.17).Fig.22 shows the variation of the SEA for the BHHs with respect toe/latv=20 m/s.Compared with the RSH,due to the introducing of joint hierarchical topologies,the BHHs have higher SEA than the RSHs.It is noted that the SEAs of the BHH—C and BHH-D are almost equal for the samee/l,and it has little sensitivity one/l.That is because these two models have the same relative density for the samee/l.However,with the increase ofe/l,the SEA of the BHH-R displays a manifest decrease,which will receive a higher value ate/l=0.334.In addition,the SEA of the BHH-R is higher than that of the BHH—C and BHH-D for the same material layout ande/l,as shown in Figs.22 and 23.The SEAs of the BHHs with H—H and S—H exhibit significantly higher value than ones with H—S and S—S,but they have the lower CLE and higher σp,as shown in Figs.14 and 16.

The energy absorption efficiency curves(that is,SEA-σout)of the BHHs with Δρ=0.115 under different impact velocities are shown in Fig.24.In the figure,σoutis the output stresses of the BHHs during the crushing,which can be given by the ratio of the contact force on fixed rigid plate to the original cross-section area of the specimen.The most effective absorbing energy structure is expected to be located in the upper-left corner of the chart.For lowvelocity impacting (v=5 m/s

Fig.21.SEAs for the BHHs under different impact velocities.

Fig.22.Effects of e/l on SEA for the BHHs with different topologies at v=20 m/s.

Fig.23.Effects of multi-material configuration on SEA for the BHHs at v=20 m/s.

Fig.24.Energy absorption efficiency for the BHHs with different topologies (⊿ρ=0.115).

4.Conclusions

In this paper,by imitating the arched shell structure of crab chela and replacing the structural joints of the RSHs with smaller arched topologies,three BHHs were designed to improve the crashworthiness and energy absorbing efficiency.The effects of hierarchical topologies and multi-material configuration on inplane dynamic behaviors of the BHHs were numerically explored.The main conclusions were drawn as follows:

(1) For the BHHs,the crushing deformation modes mainly depends upon hierarchical topology and impact velocity.Introducing of a hierarchical arched structure into the joints of the RSHs will result in changing the macro-/micro-structure deformation characteristics.For low-velocity crushing(v=5 m/s

(2) The BHHs have higher CLE than the RSHs,which is mainly related toe/l.Whene/l=0.417,the BHHs show the higher CLE,and lower σp,Δσ and ULC.The introduced hierarchical cell will deform first for the BHHs with H—S,which causes more stable collapse deformation and good crushing load uniformity.The CLE of the BHHs can be effectively controlled through the properly choice of hierarchical topolgies and multi-material layout.Moreover,empirical formulas of densification strains and plateau stresses are deduced to characterize the dynamic behaviors of the BHHs,which are in keep well with FE results.

(3) When the cell-wall thickness is same,the SEA of the BHH-R is higher than that of other hierarchical topologies under the same impact velocity,which can be improved by reducinge/l.However,the SEAs of the BHH—C and BHH-D have little sensitivity one/l.The SEA of the BHHs can be controlled bye/land multi-material layout.The SEA of the BHH-R is higher than that of the BHH—C and BHH-D for the same material layout ande/l.It is interesting that the BHH-D will have the higher energy absorbing efficiency than the BHH—C and BHH-R for the same relative density.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors are grateful for the financial support provided by the Natural Science Foundation of Hebei Province of China [No.A2020502005],the Fundamental Research Funds for the Central Universities [No.2020MS113]and Science &Technology Program of Baoding [No.1911ZG019].