步骤清晰 精准得分

文／骆丽叶

在中考阅卷过程中，阅卷细则通常要求踩点给分，即使最终答案算错，但是如果书写过程正确到位，依然会得到相应的过程分。因此，我们答题时要做到规范书写、步骤清楚，尽己所能地将分数收入囊中。

例1（2022·广东广州）如图1，点D、E在△ABC的边BC上，∠B=∠C，BD=CE。求证：△ABD≌△ACE。

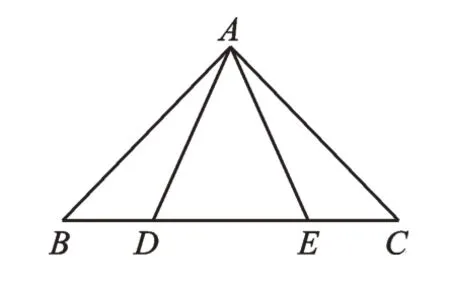
图1

证明：∵∠B=∠C，∴AB=AC。

【点评】本题是一道比较简单的几何证明题，主要考查了“等角对等边”、三角形全等的判定。

本题有2 个得分点，根据“等角对等边”可得AB=AC，是第一个得分点；用“边角边”证明△ABD≌△ACE，是第二个得分点。

例2（2020·江苏无锡）如图2，已知AB∥CD，AB=CD，BE=CF。

求证：（1）△ABF≌△DCE；（2）AF∥DE。

图2

证明：（1）∵BE=CF，

∴BE-EF=CF-EF，即BF=CE。

∵AB∥CD，∴∠B=∠C。

（2）∵△ABF≌△DCE，∴∠AFB=∠DEC。

∴∠AFE=∠DEF。∴AF∥DE。

【点评】本题主要考查了等式的性质、平行线的性质和判定、“等角的补角相等”，以及三角形全等的判定和性质。

第（1）问有3 个得分点。根据等式的性质，由已知条件BE=CF，将BE与CF分别减去公共线段，得出BF=CE，是第一个得分点；再由平行线的性质得出∠B=∠C，是第二个得分点；最后根据“边角边”证得△ABF≌△DCE，是第三个得分点。

第（2）问有2 个得分点。根据△ABF≌△DCE得到∠AFB=∠DEC，是第一个得分点；根据“等角的补角相等”得到∠AFE=∠DEF，从而AF∥DE，是第二个得分点。

例3（2022·青海）两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来，则形成一组全等的三角形，把具有这个规律的图形称为“手拉手”图形。

（1）问题发现：如图3，若△ABC和△ADE是顶角相等的等腰三角形，BC、DE分别是底边。求证：BD=CE；

（2）解决问题：如图4，若△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一条直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM、AE、BE之间的数量关系并说明理由。

图3

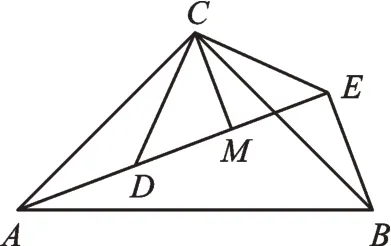
图4

（1）证明：∵△ABC和△ADE是顶角相等的等腰三角形，BC、DE分别是底边，

∴AB=AC，AD=AE，∠BAC=∠DAE。

∴∠BAC-∠DAC=∠DAE-∠DAC，

即∠BAD=∠CAE。

∴△ABD≌△ACE（SAS）。∴BD=CE。

（2）解：∠AEB=90°，AE=BE+2CM。

∵△ACB和△DCE均为等腰直角三角形，

∴AC=BC，DC=EC，∠ACB=∠DCE=90°。

∴∠ACD=∠BCE。

∴△ACD≌△BCE（SAS）。

∴AD=BE，∠ADC=∠BEC。

∵△CDE是等腰直角三角形，

∴∠CDE=∠CED=45°。

∴∠ADC=180°-∠CDE=135°。

∴∠BEC=∠ADC=135°。

∴∠AEB=∠BEC-∠CED=135°-45°=90°。

∵CD=CE，CM⊥DE，∴DM=ME。

∵∠DCE=90°，∴DM=ME=CM。

∴DE=2CM。

∴AE=AD+DE=BE+2CM。

【点评】本题是三角形综合题，主要考查了全等三角形的判定和性质、等腰三角形、等腰直角三角形的性质。

第（1）问中有4 个得分点。先根据△ABC和△ADE是顶角相等的等腰三角形，得到腰、顶角分别相等，是第一个得分点；接着由等角减去公共角得到∠BAD与∠CAE相等，是第二个得分点；再根据“边角边”证明△ABD≌△ACE，是第三个得分点；第四个得分点便是结论BD=CE。

第（2）问中有4 个得分点。先回答∠AEB的度数及线段CM、AE、BE之间的数量关系，是第一个得分点；接着根据△ACB和△DCE均为等腰直角三角形，证得△ACD≌△BCE，是第二个得分点；根据全等三角形的性质可得AD=BE，∠ADC=∠BEC，再结合等腰直角△DCE，从而可得∠BEC=∠ADC=135°，即知∠AEB=∠BEC-∠CED=90°，是第三个得分点；由CD=CE，CM⊥DE，∠DCE=90°，可得DM=ME=CM，故AE=AD+DE=BE+2CM，这是第四个得分点。我们在解这道题的时候，第（2）问即使不能求解出最终的答案，也要把前面的过程书写出来，这样可以得到一些过程分。