阿基米德水轮机阵列的耦合增益效应研究
2023-05-05郭朋华王逸远张大禹邹瀚森
郭朋华,王逸远,张大禹,邹瀚森
(西安交通大学能源与动力工程学院,710049,西安)
随着人类对深海探索需求的不断增加,出现了由深海声纳、无人潜航器等组成的深海观测网[1-3],传统的陆基和船基电缆供电方式存在使用成本高、电缆易被切断的问题,因此利用深海能源实现相关设备长周期的原位供电十分必要。深海中蕴含着多种能量形式,诸如温差能、盐差能、生物质能等[4-5],其中只有海流能具备足够大的能量密度以满足相关设备的电力需求[6]。
深海环境下流速很低,远小于常规海流能发电技术所采用的1.5 m·s-1以上的额定设计流速[7]。传统升力型水轮机低流速下的自启动能力较差,几乎很难在深海区域实现自启动[8-9];阻力型垂直轴水轮机虽然具有较好的自启动能力,但是其能量利用系数较低[10-14]。阿基米德水轮机是一种极具潜力的阻力型水平轴水轮机,具有良好的自启动性能且能量利用系数接近升力型水平轴水轮机[15],可以有效利用深海超低流速的海流能。
在实际应用中,水轮机通常采用阵列形式布置,轮机间的耦合效应可能会提高水轮机的自启动能力和能量利用系数[16]。传统升力型水轮机阵列的机组间干扰较大,排布方式对功率影响显著。Li等[17]研究了达里厄水轮机之间的水动力耦合规律,发现串联安装的水轮机阵列会大大降低下游叶片的功率系数,而并联安装时可以通过减少间距进而增加机群的总功率系数。袁鹏等[18]通过动量损失的方法对潮流能水轮机阵列进行研究,结果表明,水轮机并联间距小于4倍轮机直径时,可以更好地利用单位面积的潮流能。相较水平轴水轮机,垂直轴水轮机受湍动能影响较小,轮机之间耦合增益效果更显著。Antheaume等[19]研究了不同数量的垂直轴水轮机并联排布的影响,发现合理的排布方式能提高单台水轮机40.5%的能量利用系数。阵列中水轮机不同的旋转方向对轮机间的耦合效应也有影响。安琪[20]分析了不同排布方案对水轮机阵列功率及性能的影响规律,发现旋转方向相反的水轮机可以提高阵列整体性能。Bai等[21]数值研究了不同排布方式下的水平轴水轮机转向和间距对性能的影响,结果表明,直线网格阵列中反向旋转对水轮机的影响大于交错网格阵列的影响,并且反向旋转的影响随着水轮机下游距离的增大而迅速减小。部分学者基于对尾迹区的流场分析,认为交错排布阵列可以利用被加速的尾流,有可能提高水轮机的能量利用系数。于书帆等[22]数值研究了双水轮机在不同轴间距、相对位置角和不同尖速比情况下的各项性能参数,与孤立轮机相比,双水轮机交错排布的能量利用系数大于孤立轮机的能量利用系数,但由于尾流涡列区较长,尾流速度恢复所需距离也较长。
综上所述,水轮机的阵列布置可能带来耦合增益效应,从而提升整体机群的功率输出,然而迄今为止没有文献对阿基米德水轮机阵列进行研究。因此,本文通过数值模拟的方式开展阿基米德水轮机的阵列耦合增益研究,为该类型轮机阵列的优化布置策略提供参考。
1 数值模型
1.1 几何模型建立
本文采用的阿基米德水轮机如图1所示,本项目组前期对孤立轮机进行了优化设计,其具体几何参数如表1所示。
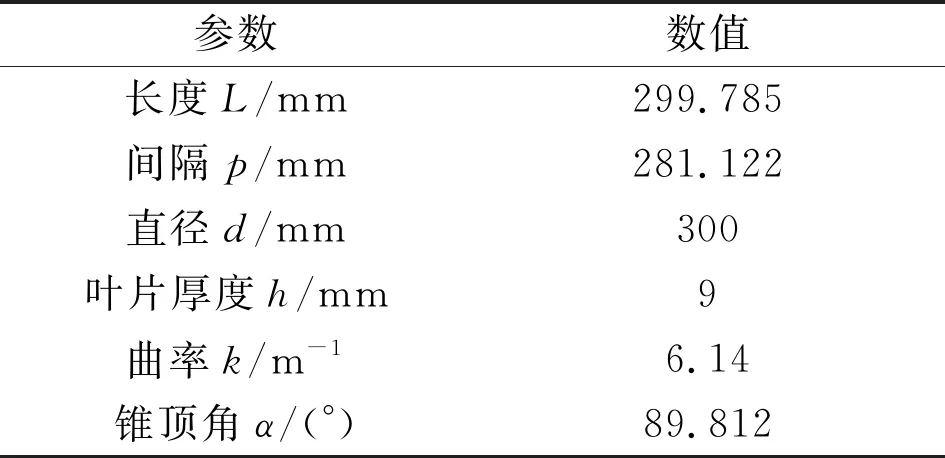
表1 阿基米德水轮机几何参数
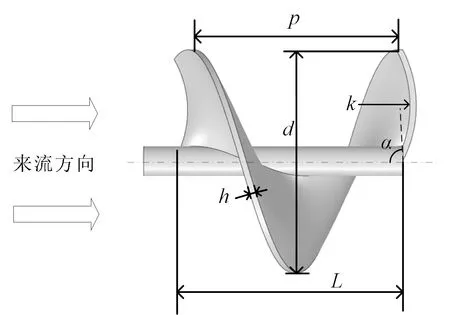
图1 阿基米德水轮机几何参数示意图Fig.1 Geometrical parameters of the Archimedes turbine
1.2 计算域建立
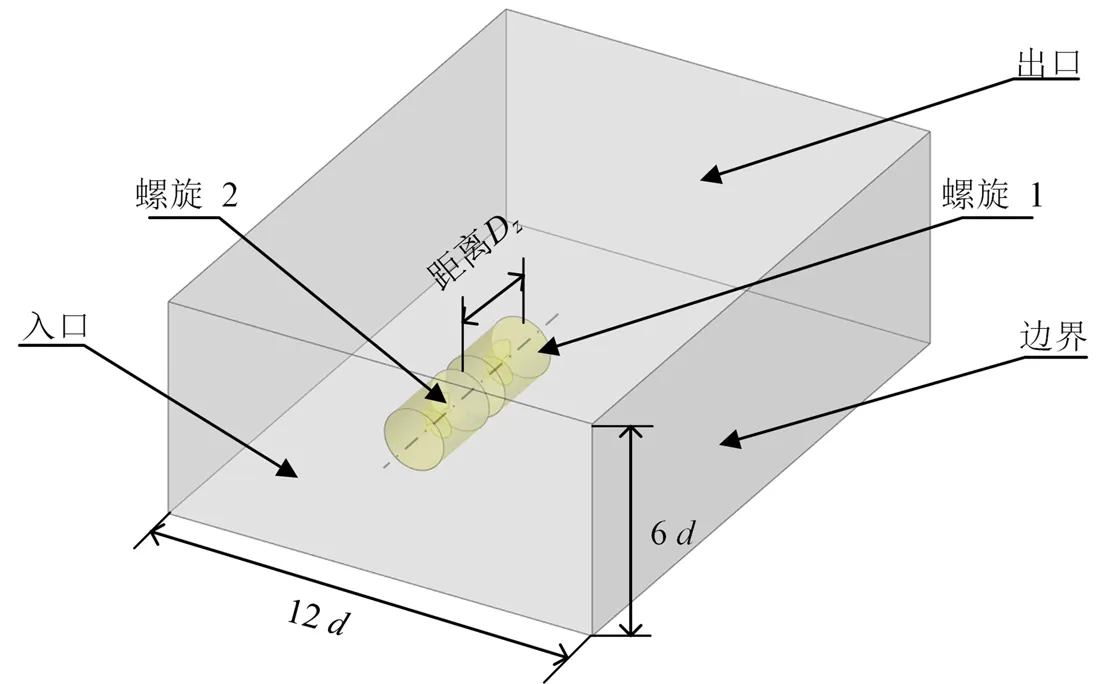
利用ANSYS SpaceClaim建立计算域,坐标原点位于螺旋1叶片底部。正对来流方向的流域横截面尺寸为12d×6d,螺旋叶片前沿距入口2d,后端距出口10d,具体尺寸如图2所示。

(a)并联阵列
(b)串联阵列
1.3 计算设置及边界条件
采用四面体网格划分,并对阿基米德螺旋叶片周围进行局部网格加密,边界层为20层,调整第一层边界层的厚度,以得到接近1的y+值。在计算设置上,采用二阶迎风算法,湍流模型为SSTk-ω模型。选取水作为流体介质,密度为998.2 kg·m-3,动力黏度为10-3Pa·s,入口速度为0.5 m·s-1,出口设置为压力出口,相对压力为0。速度分量和湍流性质均采用10-5的收敛标准。
水轮机的能量利用系数和启动力矩系数是水轮机重要的性能特征,尤其是部署在深海的水轮机,良好的启动力矩系数可以在一定程度上简化控制系统和额外的机械装置。能量利用系数Cp、启动力矩系数Ct,s和叶尖速比λ计算式为
(1)
(2)
(3)
式中:T为力矩,N·m;ω为转速,rad·s-1;ρ为流体密度,kg·m-3;R为水轮机半径,m;V为来流速度,m·s-1。
1.4 数值模型无关性验证
为了保证数值模拟结果的准确性,本文进行了网格无关性验证、时间步长无关性验证和计算区域无关性验证。对单个阿基米德螺旋轮机进行不同网格尺寸划分,以性能指标Cp、Ct,s作为判断指标,网格数量及计算结果如表2所示。当网格数量为133万时,Cp、Ct,s的波动幅度低于1.5%,继续增大网格数量对计算结果影响较小。时间步长的影响如表3所示,当时间步长为0.01 s时,Cp、Ct,s的波动幅度低于1%,缩小时间步长对计算结果影响不大。对不同尺寸的计算区域进行无关性验证结果如表4所示,选择图2所示计算区域尺寸为参考值。当计算区域缩放比例为1.1时,Cp、Ct,s的波动幅度低于1%,扩大计算区域面积对计算结果影响不大。故在保证计算精度的前提下本文依据图2的计算区域,选择133万级别的网格和0.01 s的时间步长进行数值模拟。

表2 网格无关性验证

表3 时间步长无关性验证

表4 计算区域无关性验证
1.5 实验验证
为了进一步验证数值模型的准确性,对阿基米德水轮机进行了循环水槽实验。实验装置示意图如图3所示,实验段来流面积为0.5 m×0.8 m,长为1 m,实验流速为0.5 m·s-1。阿基米德水轮机的螺杆水平置于实验段的中心,阻塞比为17.7%,采用钝体水槽修正方法[23-24]补偿阻塞比带来的影响,结果对比如图4所示,数值模拟结果与修正后的实验数据吻合较好,验证了本文数值模拟方法的可靠性。

图3 实验装置示意图Fig.3 Diagram of experimental device

图4 数值模拟结果与实验数据对比Fig.4 Validation of Cp between experiment and simulation
1.6 速度控制策略
以往文献中关于水轮机阵列研究,通常将阵列中的轮机设置为相同的转速以便计算,然而实际中由于不同位置处的水轮机来流速度不同,因此阵列中各轮机的最优工作转速也应该是不同的。本文通过计算得到不同流速下最佳功率输出所对应的转速,采用多项式拟合的方法获得孤立轮机的最佳功率曲线。利用Fluent中用户自定义函数UDF对阵列中的孤立轮机进行转速控制,通过迭代计算使转速匹配到最佳功率,计算流程如图5所示,其中系数随时间变化:当t≤10时,r=0.5;当10
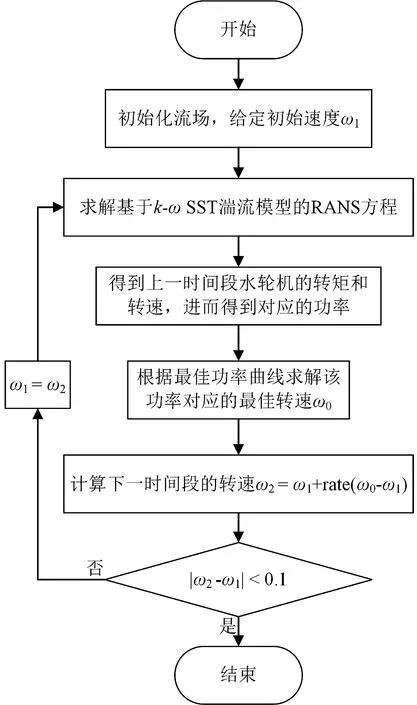
图5 速度控制框图Fig.5 Flow chart of the speed control method
2 并联与串联阵列耦合增益研究
2.1 并联阵列
2.1.1 并联阵列能量利用系数
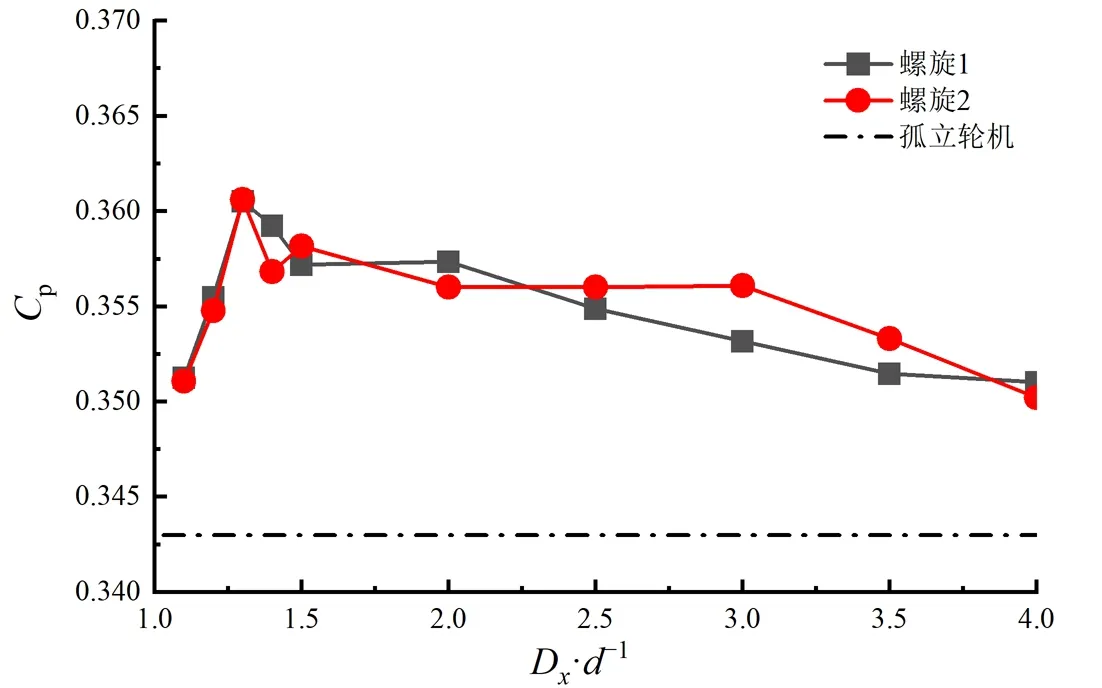
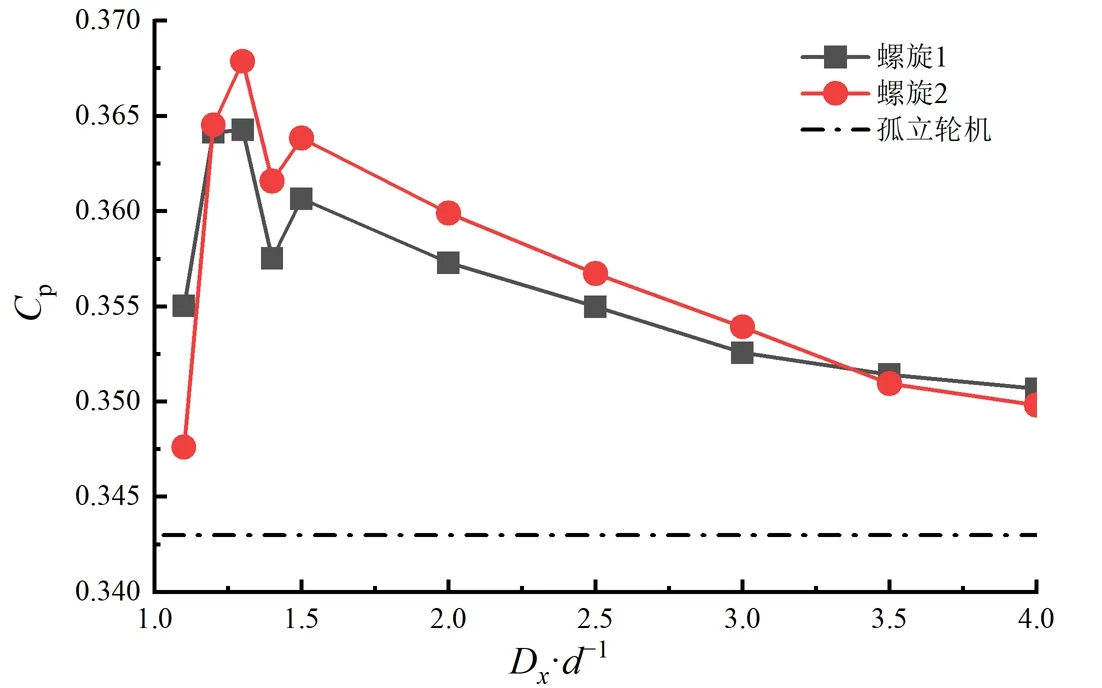
对并联的阿基米德水轮机阵列,分别进行同向和反向旋转布置,计算结果如图6所示。
阿基米德水轮机并联阵列中单个轮机的Cp均有不同程度的提高,同向和反向旋转布置的轮机阵列的Cp在距离Dx=1.3d时均达到峰值,分别较孤立轮机的Cp提升了5%、7%。随着距离Dx的增加,在1.5d之后两种旋转方向的水轮机的Cp均逐渐减小,直至接近孤立轮机的Cp。
(a)同向旋转
(b)反向旋转
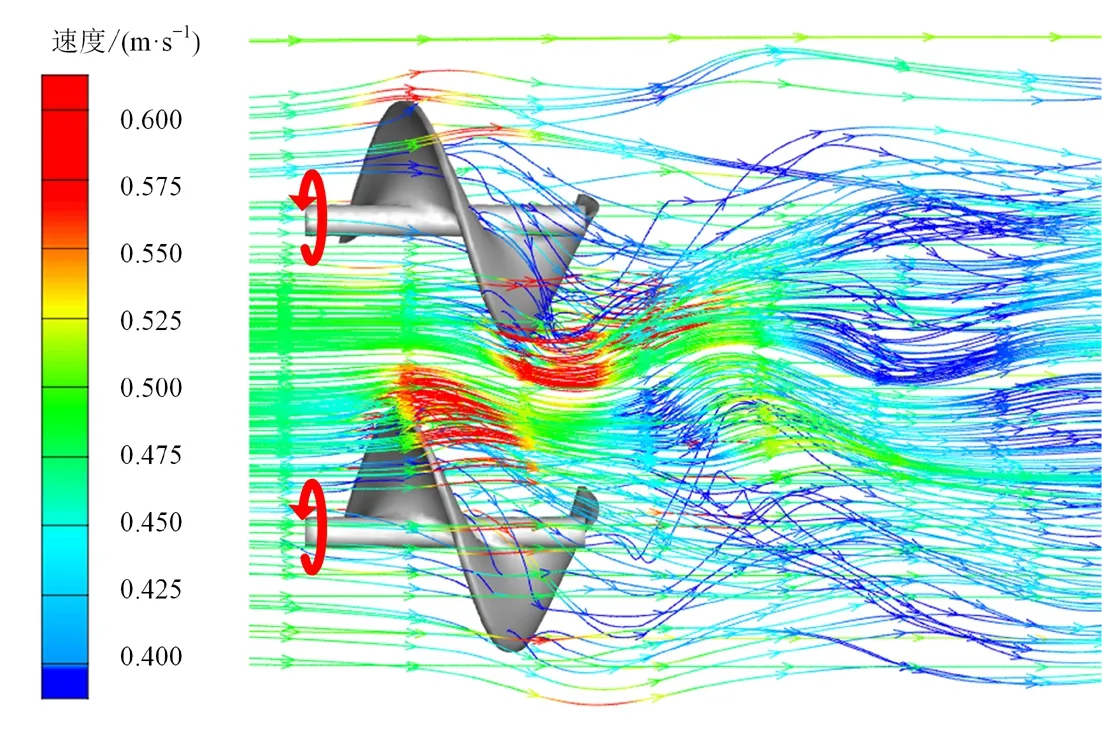
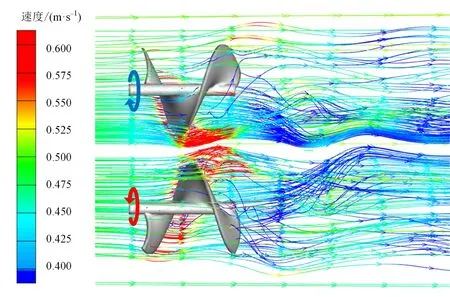
并联阵列间距Dx=1.3d时的流场如图7所示,图中上方轮机为螺旋2,下方轮机为螺旋1,两台并联轮机的周围形成高速区,中间流域的加速效果尤为显著。由于阿基米德水轮机具有一定的轴向长度,所以受阻塞效应影响,阿基米德水轮机会在入流面和侧面持续受到位于中间流域加速区的影响,从而获得高于孤立轮机的性能参数。此外,根据角动量
(a)同向旋转
(b)反向旋转
守恒,旋转轮机的周围会产生与之转向相反的尾流,同样由于阿基米德水轮机的轴向长度,相反转向的尾流会出现在水轮机的侧面和尾流面。反向旋转阵列中的轮机尾流会与相邻轮机产生啮合效应,所以在轮机间距较小时,反向旋转阵列的能量利用系数大于同向旋转阵列的能量利用系数。
随着Dx的不断增加,这种增益效果逐渐减小,当Dx=4d时,Cp较孤立轮机仅提高2%;当Dx小于1.3d时,轮机之间的干涉影响逐渐显著。
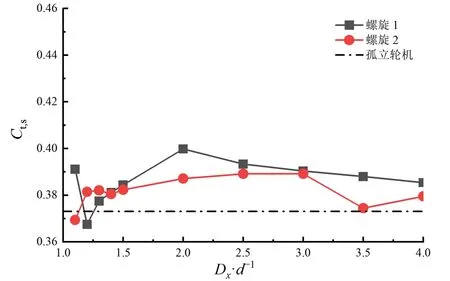
2.1.2 并联阵列启动力矩系数
并联阵列的Ct,s如图8所示,相比反向安装,同向安装阵列的自启动性能更为优越,其Ct,s大于孤立轮机,同样是在间距为Dx=1.3d附近达到峰值,螺旋2的Ct,s较孤立轮机提升了19%。随着距离Dx的不断增大,Ct,s逐渐接近孤立轮机。综合考虑Ct,s、Cp,并联阵列的间距应该选择在Dx=1.3d左右。

(a)同向安装
(b)反向安装
2.2 串联阵列
2.2.1 串联阵列能量利用系数
对串联的阿基米德水轮机阵列,同样进行同向和反向旋转布置,结果如图9所示。
(a)同向旋转
(b)反向旋转

图10 串联阵列同向旋转速度云图Fig.10 Velocity contour of the serial array with the same rotation direction
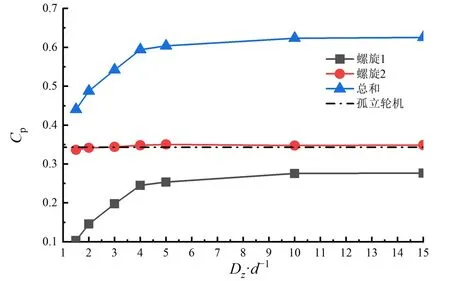
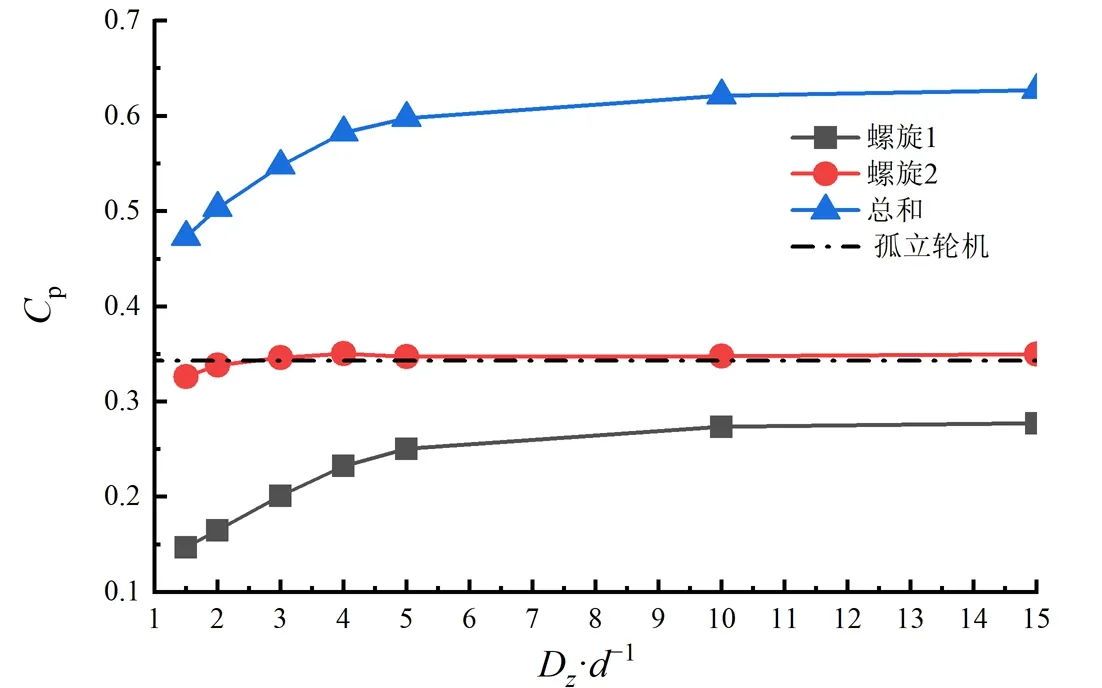
阿基米德水轮机串联放置时,随着间距的不断增加,上游轮机在Dz=3d时恢复到孤立轮机的Cp,此后基本不受下游轮机的影响。下游轮机的Cp随距离的增加先快速上升,当间距Dz=5d时恢复到孤立轮机Cp的70%,随后上升趋势明显变缓,当间距Dz增加到10d时,Cp恢复到孤立轮机的80%,对应的流场尾迹速度云图如图10所示。虽然在Dz=5d处的流场仍存在较强的尾迹涡,但是下游阿基米德轮机已经能够恢复至较高的Cp,这是由于阿基米德水轮机运行尖速比较低,受湍动能的影响较小。而在较高尖速比运行下的升力型水平轴水轮机中,串联阵列要获得类似的恢复效果通常间距要在8d以上[25],以上结果表明阿基米德水轮机可以组成更为密集的串联阵列,从而最大化阵列的能量密度。
2.2.2 串联阵列启动力矩系数
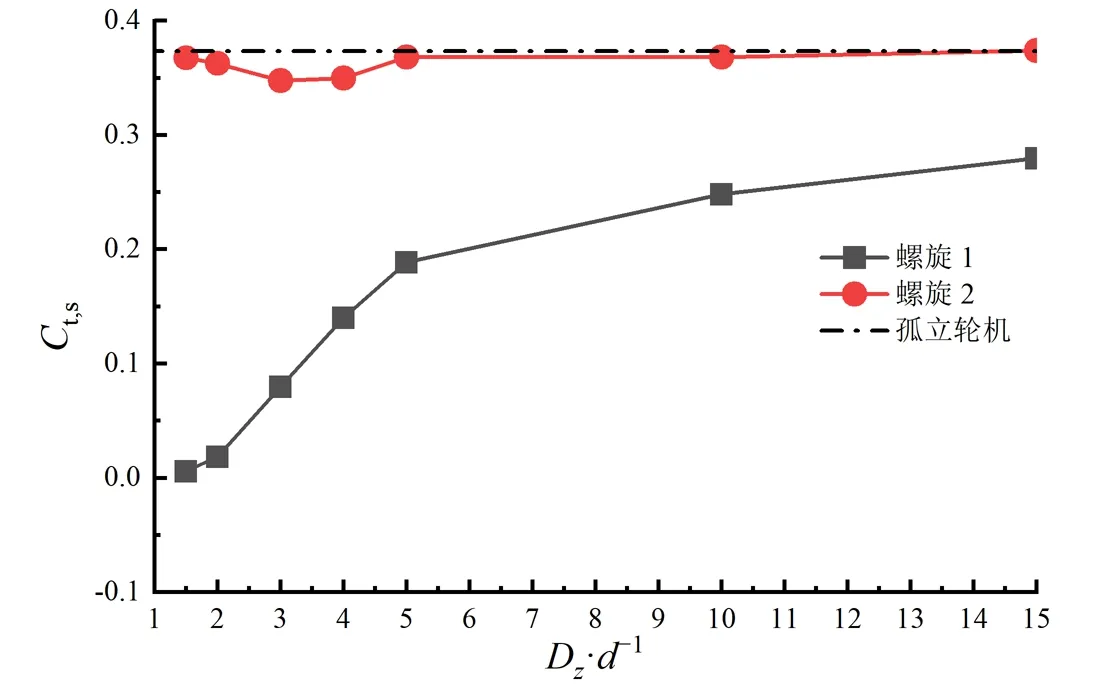
不同放置间距下的Ct,s如图11所示。无论是同向还是反向安装,上游轮机在Dz=3d时Ct,s均出现最小值,随后逐步恢复至孤立轮机的Ct,s。下游轮机的Ct,s随间距的变化情况与Cp类似,在间距Dz=5d之前快速上升,随后增长趋势变缓。特别需要注意的是,在距离Dz小于2d时下游轮机的Ct,s极低,对于同向安装间距为1.5d、2d时甚至出现了Ct,s为负数的工况,此时上游轮机的尾流效应会严重影响下游轮机的自启动性能。

(a)同向安装
(b)反向安装
3 交错排布水轮机阵列性能研究
通过对并联阵列和串联阵列的研究,可以发现上游轮机的尾流效应和相邻轮机间的阻塞效应是影响水轮机Cp、Ct,s的主要因素。因此,可以采用交错的阵列排布方式,一方面可以减少尾流低速区的影响,另一方面可以有效利用阻塞的耦合增益效应。
本文以典型的三角阵列排布方式为研究对象,以垂直于来流方向间距Dx和平行于来流方向间距Dz为研究变量,分析了两种不同旋转方案下三角形阵列的耦合增益效应,两种旋转方案如图12所示。
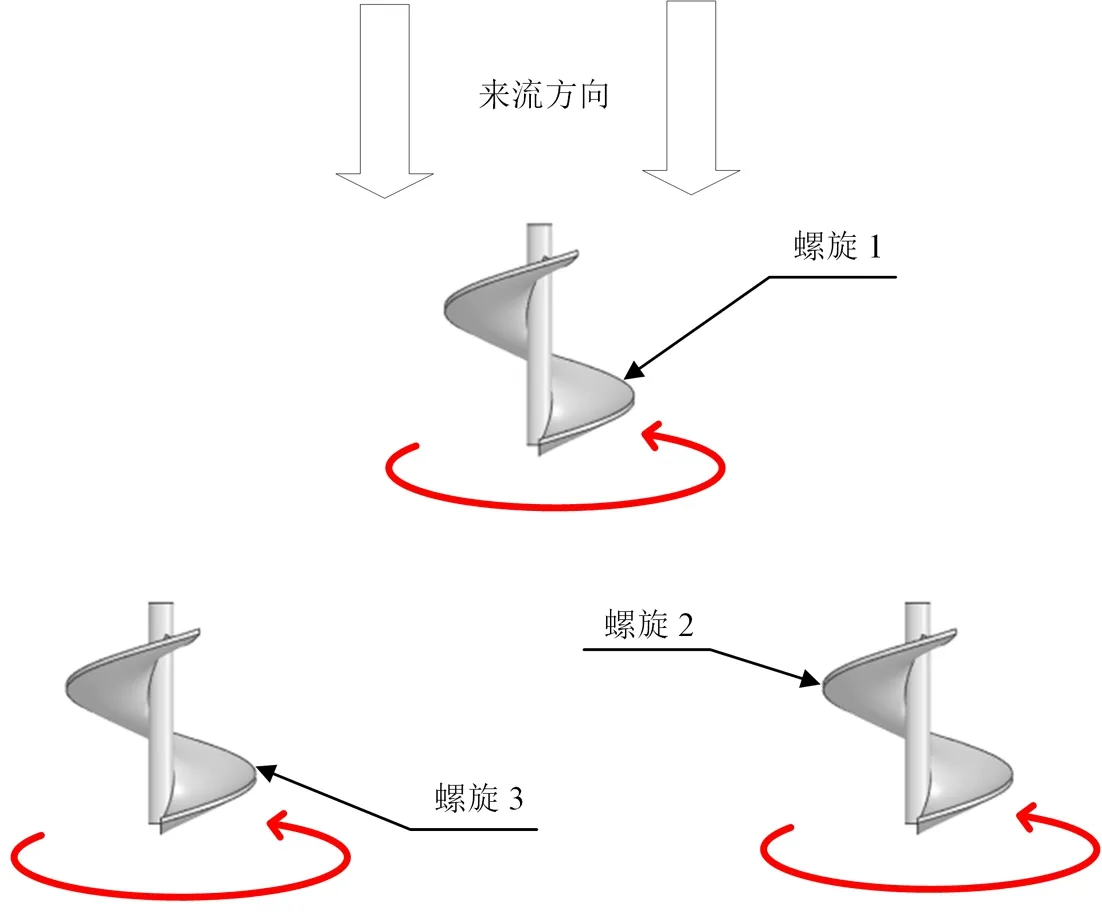
(a)同向旋转

(4)

同向、反向旋转阵列中各轮机Cp分别如图13、图14所示。对于同向旋转布置,当列间距Dx小于d时,过小的间距使得下游轮机处于尾流效应明显的区域,此时上游轮机尾迹的不利影响超过了轮机间的耦合增益效应,使得下游轮机的Cp均低于孤立轮机;当Dx=1.2d时,只有在行间距Dz小于3d的情况下才会高于孤立轮机。随着列间距Dx的继续增大,下游轮机的Cp均高于孤立轮机,当Dx=2d时,Cp出现峰值,较孤立轮机提升6%,此时尾流效应影响较小,而下游轮机之间以及下游与上游轮机之间均存在较强的耦合增益效应。反向旋转布置时下游轮机Cp的变化趋势与同向旋转相似,但峰值出现在Dx=1.2d处,较孤立轮机提升8%。
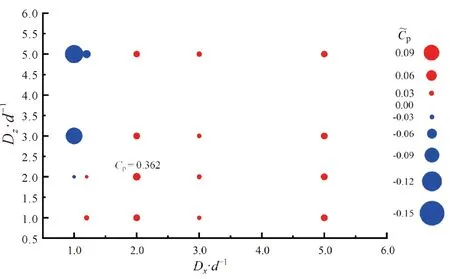
(a)螺旋2能量利用系数

(b)螺旋3能量利用系数

(a)螺旋2能量利用系数

(b)螺旋3能量利用系数
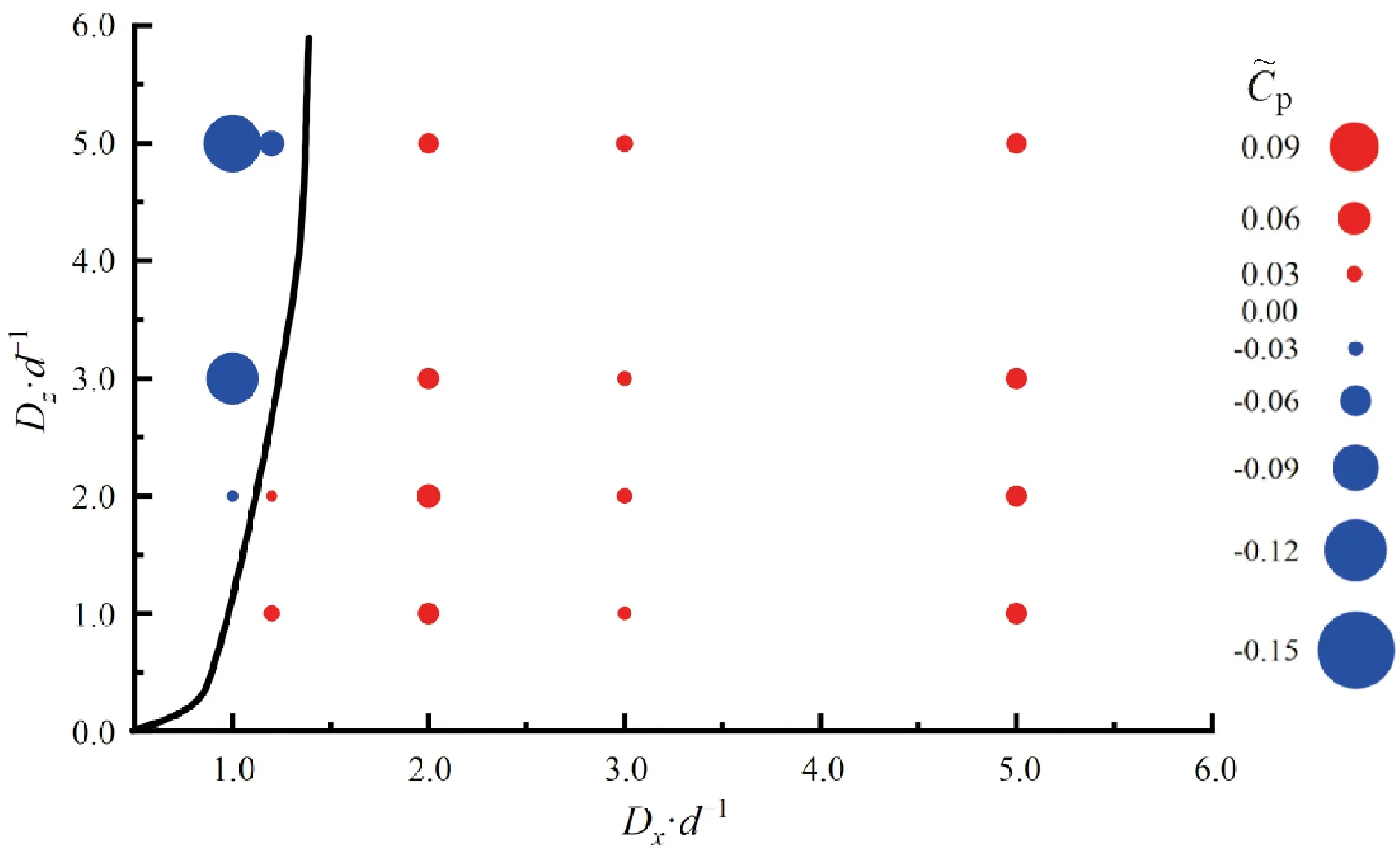
(a)同向旋转
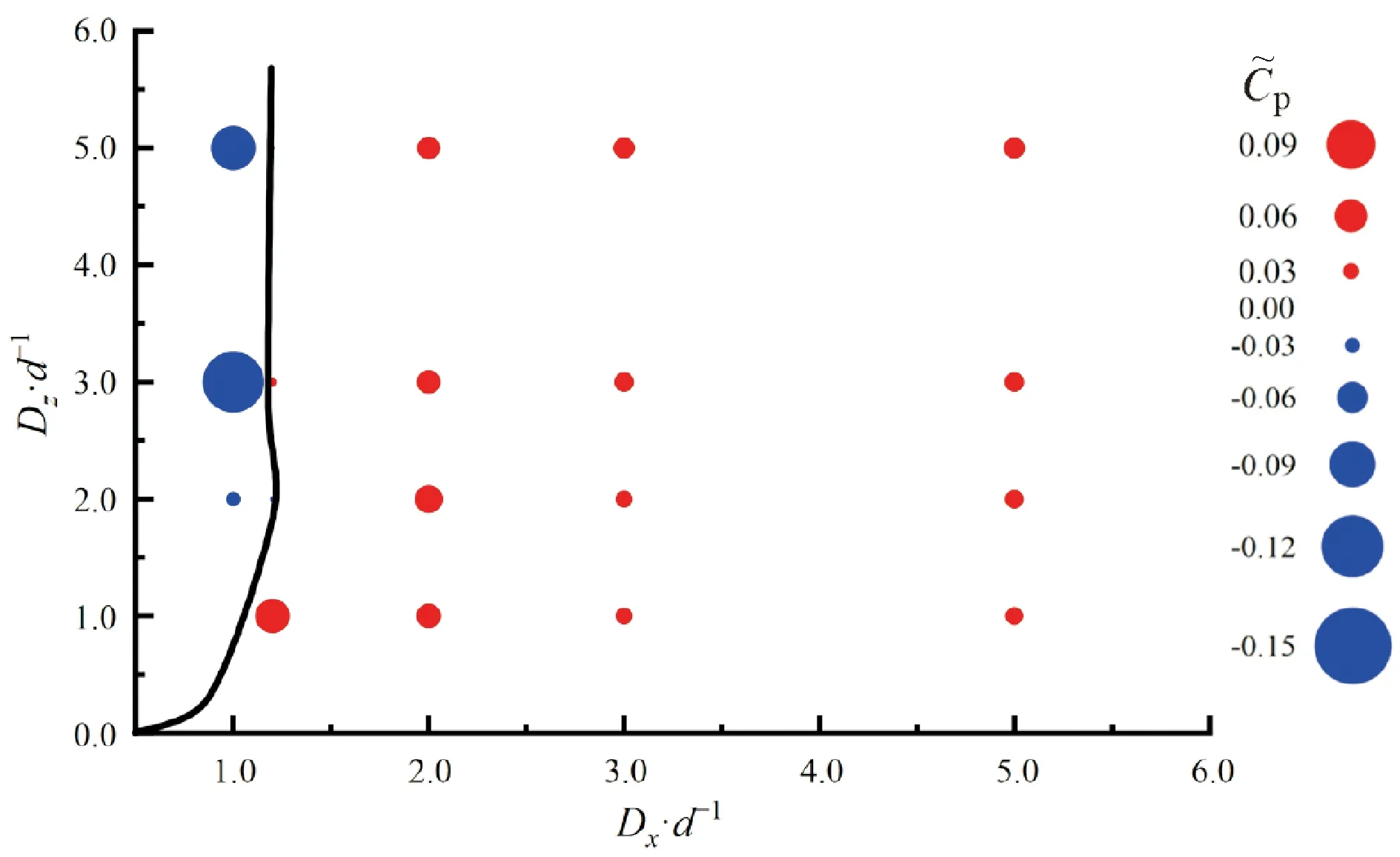
(b)反向旋转
Fig.15 Diagram of coupling gain boundary of triangular arrays
4 结 论
(1)受益于耦合增益效应,并联阵列条件下轮机的功率输出和自启动性能均有提升。反向旋转时耦合增益最大,在间距为1.3d时Cp提升至孤立轮机的107%;同向旋转时轮机具有更高的Ct,s,在间距为1.3d时可以提升至孤立轮机的119%。
(2)受尾迹效应影响,串联阵列中上游轮机的Cp、Ct,s略有降低,在间距大于5d时恢复至接近孤立轮机的水平;下游轮机的Cp、Ct,s均出现明显下降,在间距大于5d之后恢复趋势变缓,Cp恢复至孤立轮机Cp的70%。
(3)受耦合增益和尾迹效应的综合作用,三角形阵列在保持一定间距的条件下,可以使Cp得到8%的提升。上游轮机和下游轮机进行反向旋转布置既可以获得较大的功率提升,又能够实现紧凑布置。
