叶片安装角偏差对动叶性能影响的不确定性研究
2023-05-05李玉楚武利姬田园
李玉,楚武利,姬田园
(西北工业大学动力与能源学院,710129,西安)
叶片是构成压气机的基本结构单元,对流过压气机的气流进行加功,以此提高压气机出口的气流压力。压气机动叶旋转和气流发生能量转换,将一部分能量转化为压力的升高。压气机叶片的生产质量与几何型面的精度在很大程度上直接决定着航空发动机的工作性能,因此有必要针对压气机叶片加工误差影响气动性能的问题开展研究。在2003年,Garzon等[1]检测了压气机大量实体叶片,将实际测量的叶型数据与设计叶型进行对比可看出,实际叶片实体与理论叶型存在不同程度的偏差。
国内外学者对扭转度误差进行了较多的研究表明,叶型扭转对压气机影响较大。高丽敏等[2]采用数值模拟手段得出,0.5°的叶型扭转角偏差造成的损失增加高达46.56%。郑似玉等[3-4]对某多级高压压气机的后面级,采用数值模拟方法和高斯概率密度函数的理论分析相结合的方法,选取扭转度、位置度、轮廓度3种典型加工偏差进行敏感性分析。郑覃等[5]针对跨声速压气机转子,采用准二维的数值方法,进行对最大厚度位置、安装角等的敏感性分析发现,安装角偏差对激波结构、叶型表面附面层厚度的影响最为显著。Lange等[6-8]研究了动叶安装角、最大厚度对高压压气机气动性能的影响。Lebele等[9]研究表明,叶片的扭转会导致气流转折角增加,从而增加压气机的耗功,降低压气机的等熵效率。Fathi等[10]对涡轮叶片的扭转度、位置度、前尾缘厚度及轮廓度这4种偏差进行了敏感性分析。Bammert等[11]研究表明,安装角的加工误差对出口气流角的变化相对较大。
压气机在运行过程中,进出口气流条件、模型、叶表粗糙度和叶片几何参数的随机性均会严重影响压气机性能。Garzon等[1]对压气机叶片的大量测量数据表明,加工误差表现出高度的随机性,会导致叶片几何不确定性,进而对压气机气动性能造成不确定性的影响。由于确定性分析没有考虑到不确定性因素的影响[12],近年来,国内学者针对加工偏差的不确定性问题展开了大量研究,并自主发展了多种数学方法应用其中。郭正涛等[13]提出了一种由法向加工误差导致的叶片表面几何不确定性降阶模型,通过给定加工误差分布的标准差函数求解该模型,并对该模型概率分布构成的空间使用Halton抽样,最终训练自主发展的人工神经网络作为代理模型,分析某高负荷压气机叶栅的几何偏差影响。郭正涛等[14]还发展了基于高斯分布型输入的非嵌入式混沌多项式,研究分析端壁倒圆半径误差对叶栅性能的不确定性影响。罗佳奇等[15]建立了基于伴随方法的叶片加工偏差不确定性灵敏度分析方法,结合罗特卡罗方法,得到气动性能的概率密度函数分布,该方法可以用来预测加工气动性能偏差。傅珏等[16]研究叶顶间隙几何不确定性对Krain离心叶轮效率、压比性能统计变化规律的影响。赵轲等[17]研究表明,混沌多项式方法能大幅提高稳健型优化设计效率。由此可见,不确定性方法众多,其中多项式混沌法在低维不确定性求解问题中得到了广泛应用,多项式混沌法分为嵌入式混沌多项式(IPC)和非嵌入式混沌多项式(NIPC)。IPC需要对模型进行大量修改,而NIPC采用已有的数值模拟程序,不需要对控制方程和程序进行修改,其应用更为广泛[18]。
目前对安装角不确定性影响的研究甚少,本文采用自主编制的非嵌入式混沌多项式(NIPC)程序,将基于NIPC的不确定量化分析应用到叶片安装角偏差对跨声速压气机转子的不确定性影响的研究中。将NIPC结合蒙特卡罗抽样,获得输出变量的概率分布和统计值,探讨安装角偏差与性能的相关性,继而得到安装角偏差与总压比和绝热效率的函数关系式。本文分别在峰值效率工况和近失速工况下进行流场分析,并结合耗散函数说明安装角偏差对动叶损失的不确定性影响机理,有利于深刻认识安装角偏差对压气机气动性能和流场的影响,同时为分析叶片加工偏差对压气机的不确定性影响提供理论基础。
1 研究对象及方法
1.1 研究对象
本文研究对象是跨声速轴流压气机转子NASA Rotor 37,由NASA Lewis研究中心为研究载荷和展弦比对压气机气动性能的影响而设计,它拥有大量的实验数据[19],对于开展理论研究有重要的指导意义。该转子的主要气动设计参数和几何结构参数如表1所示。

表1 Rotor 37的设计参数
1.2 数值方法及验证
采用NUMECA中Fine/Turbo模块进行三维定常数值计算,进口边界条件给定总温为288 K,总压为101 325 Pa,采用轴向进气,出口边界给定背压,固体壁面为绝热无滑移边界。经过数值校核,本文采用SA湍流模型,时间离散格式为二阶迎风格式。网格划分通过Autogird5模块完成,总网格数为107万,主通道网格拓扑为O-4H型网格拓扑结构。
主通道沿轴向、径向和周向的网格点数分别为195、97、55,叶顶间隙采用蝶形网格拓扑结构,点数设置为41。如图1所示,第一层尺度设置为3×10-6m,使得y+小于2。在近失速工况下,出口处的周向平均总压比和绝热效率沿径向分布的对比见图2。计算结果与实验结果整体趋势上吻合良好,较好地反映了总压比和效率的径向分布规律。
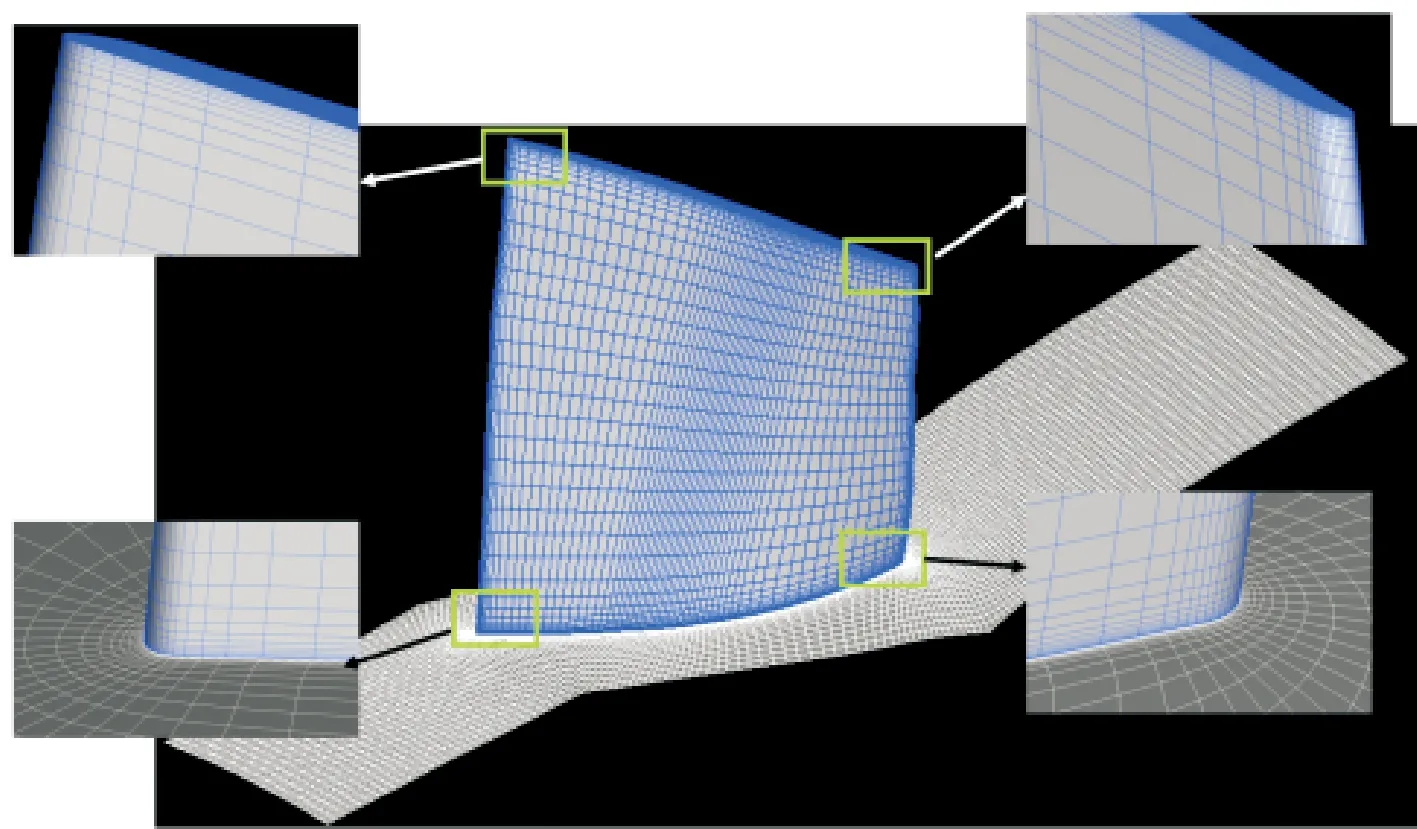
图1 Rotor 37 网格示意图Fig.1 Grid diagram of Rotor 37
图3给出了近失速工况下,95%叶高截面相对马赫数分布对比,发现数值模拟所捕获的通道中的激波结构、位置及叶顶泄漏涡涡核轨迹与实验大致吻合,说明数值模拟结果可靠。
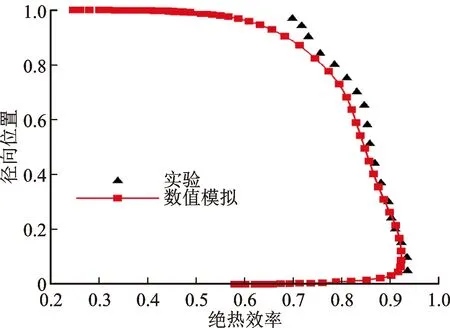
(a)绝热效率

(b)总压比
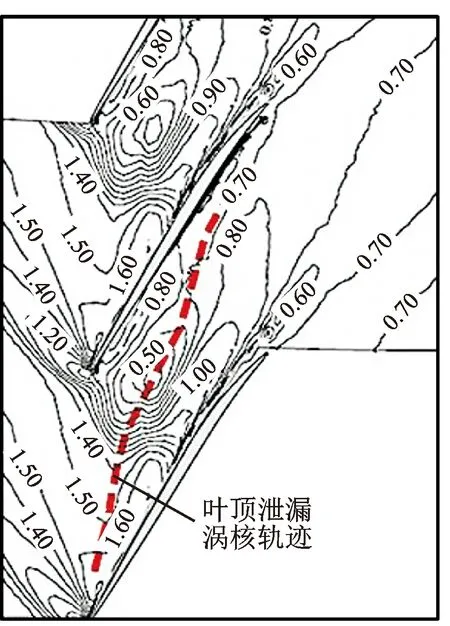
(a)实验
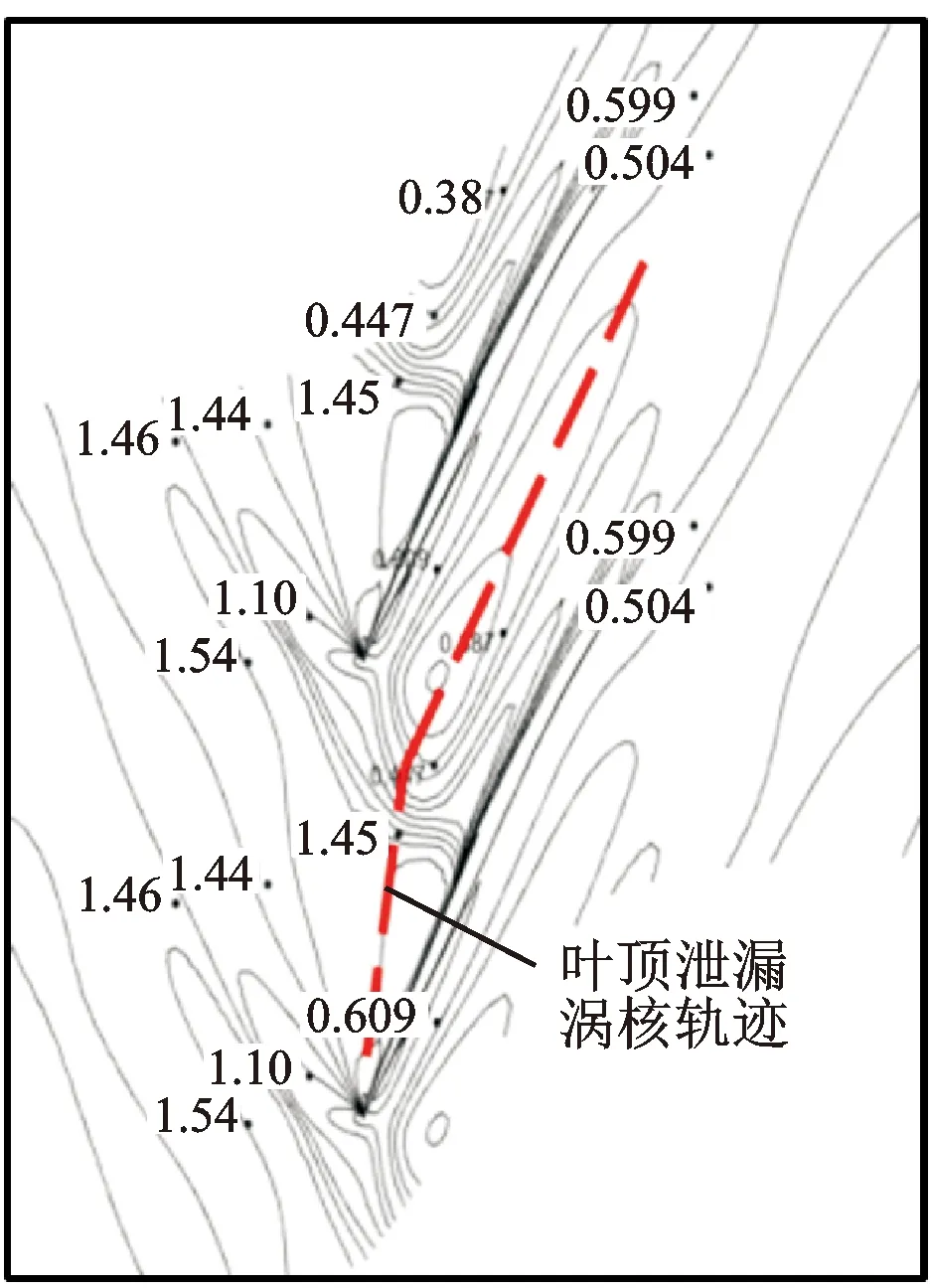
(b)数值模拟
1.3 安装角偏差概率分布
叶片安装角偏差指叶片在加工时所产生的角向位置偏差,即叶片绕积叠轴旋转的角度,本文认为叶片的积叠轴为各叶高截面重心的连线。安装角偏差为负代表叶片安装角“关闭”,叶片绕积叠轴顺时针旋转。安装角偏差为正代表叶片安装角“打开”,叶片绕积叠轴逆时针旋转。已有研究表明[20],当叶片数量足够多时,加工偏差满足正态分布,因此认为本文所研究的安装角偏差服从零均值的正态分布,概率密度函数为

(1)
式中:a为均值;δ2为方差。
根据文献[21]指出,叶型的安装角偏差β是指叶型绕顺时针方向转动0.5β、逆时针方向转动0.5β形成的角度。推荐的安装角偏差如表2所示,选取5级精度等级,安装角偏差β为1°,则安装角正负变化0.5°。根据正态分布的3δ原则,在±3δ的误差范围内其置信区间可达整个误差范围的99.74%,选择置信区间为(-0.5°,0.5°),则安装角偏差分布服从正态分布N(0,0.166 7)。

表2 叶型安装角公差精度等级
2 不确定量化方法
本文采用自主编制的非嵌入式混沌多项式(NIPC)程序对不确定性量化方法展开研究。根据Wiener的研究[22],多项式混沌本质上是用多项式对随机变量进行级数展开,并将随机变量的随机特性转移到多项式系数上,通过求解多项式系数,可以得到输出变量的统计学意义的变量。
选用Hermite正交多项式构造多项式Z(θ),设Z(θ)是概率空间上关于随机变量θ的随机过程,则
(2)
式中:Hn(ξi1,…,ξin)是随机变量ξ=(ξi1,…,ξin)的n阶Hermite多项式,表达式为
(3)
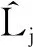

(4)
式中:参数P由多项式有限阶数j和变量有限维数k共同决定
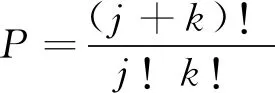
(5)
接下来通过Galerkin投影法求得混沌多项式展开系数
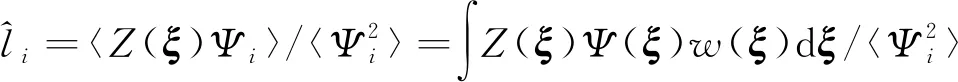
(6)
式中:〈〉表示内积;w(ξ)代表正交多项式的权函数。
采用Gauss-Hermite数值积分公式计算式(16)后,式(6)可写为
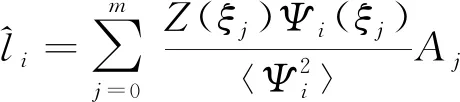
(7)
式中:m为积分点个数;Aj为对应各采样点的积分权值,表达式为

(8)
由此可以得到混沌多项式各项系数。然后,根据Hermite多项式的正交性,易求得输出变量的均值和标准差分别为
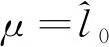
(9)

(10)
本文研究的叶型误差为单变量误差,故选取一元非线性试验函数对不同NIPC阶数的精度进行检验,试验函数如下
Y=f(x)=

(11)
式中:x服从N(0,1)分布。
当采集的样本数量足够多时,认为蒙特卡罗抽样(MCS)方法所模拟的结果能够代表理论结果,可以检验NIPC的精度。蔡宇桐课题组研究得出4阶或5阶NIPC方法基本满足精度要求[23]。表3给出了使用不同阶数的NIPC方法和MCS方法针对试验函数的统计结果,其中N1代表使用MCS方法所需要的样本数量,N2代表使用NIPC方法所需要的样本数量,e2代表NIPC模型响应与试验函数相应的均方误差,它可以表征NIPC输出的拟合函数对试验函数的拟合精度。试验函数中的变量x服从N(0,1)分布,自变量在±3δ的变化范围占完整正态分布概率的99.73%,x在[-3,3]内等距取1 001个点,e2定义如下
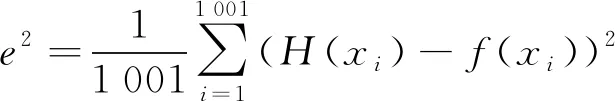
(12)
式中:H(x)为多项式混沌展开式。
从表3中看出,相较于MCS方法,使用NIPC方法明显可以大幅度降低样本数量,提升计算效率。对比不同阶数的NIPC发现,当NIPC阶数为5时,均值为3.654 024 6,且均方误差的精度达10-8量级。随着阶数提高到6,均值保持不变,均方误差的精度量级依旧是10-8。阶数提高到7时,均值保持不变,均方误差的精度达10-10量级。考虑到5阶NIPC方法计算精度已足够高,且能节省计算时间,因此,本文选用6点5阶NIPC方法进行不确定性分析。
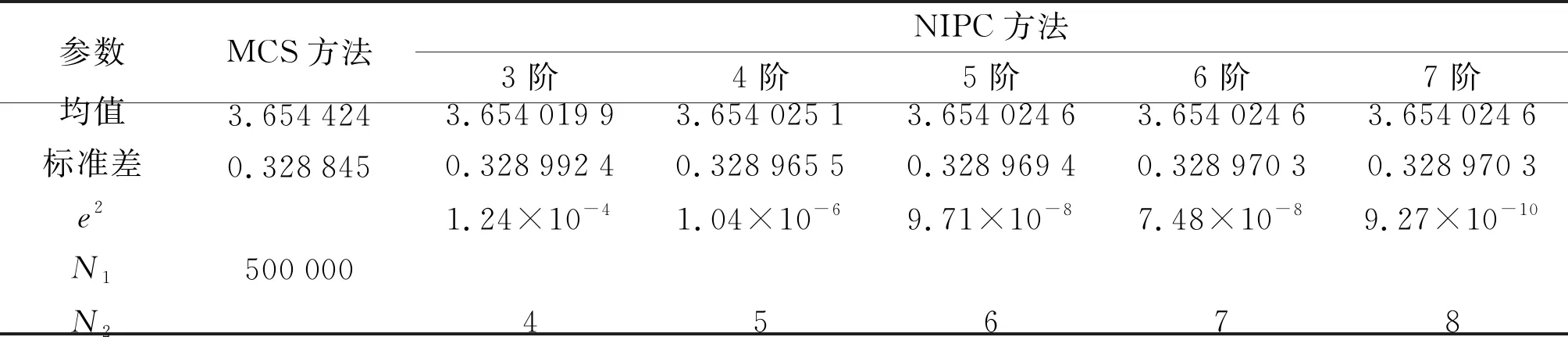
表3 一元非线性试验函数试验结果
3 结果与讨论
3.1 气动性能统计分析
统一质量流量进行统计学分析,选取质量流量20.61 kg/s为峰值效率工况,质量流量18.84 kg/s为近失速工况。在给定流量的条件下,分别在峰值效率工况和近失速工况下进行性能的统计分析。
在不确定量化分析过程中,可以使用具有统计意义的变量来评价误差影响。均值μ表示性能或稳定性相对于原型的平均偏移程度,标准差δ用于量化性能或稳定性受误差不确定性影响偏离均值的波动程度,引入标准差与均值的比值δ/μ来除去均值的影响,表示受误差影响的敏感性。图4给出两工况下具有安装角偏差时总压比π和绝热效率η的均值μ与原型值的比较,发现安装角偏差的波动几乎不会对性能的平均水平造成影响。
图5展示了峰值效率工况(PE)和近失速工况(NS)下转子性能参数的δ和δ/μ。从图中看出,安装角偏差对气动性能的影响程度与所处工况有关,NS绝热效率的δ和δ/μ均大于PE绝热效率。这说明安装角偏差不确定性对近失速工况下绝热效率的影响更大,也说明近失速工况下的损失受安装角不确定性的影响扰动更强。PE总压比的δ和δ/μ大于NS总压比,说明PE工况下的总压比相比较NS工况对安装角偏差的不确定性更敏感。近失速工况下,绝热效率的相对波动幅度相比较峰值效率工况增加了22.95%,峰值效率工况下,总压比的相对波动幅度远大于近失速工况。综上可知,安装角误差对转子性能的平均水平造成的影响微弱,但会影响转子性能的波动程度。
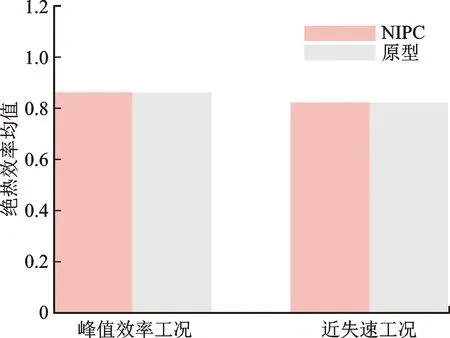
(a)绝热效率
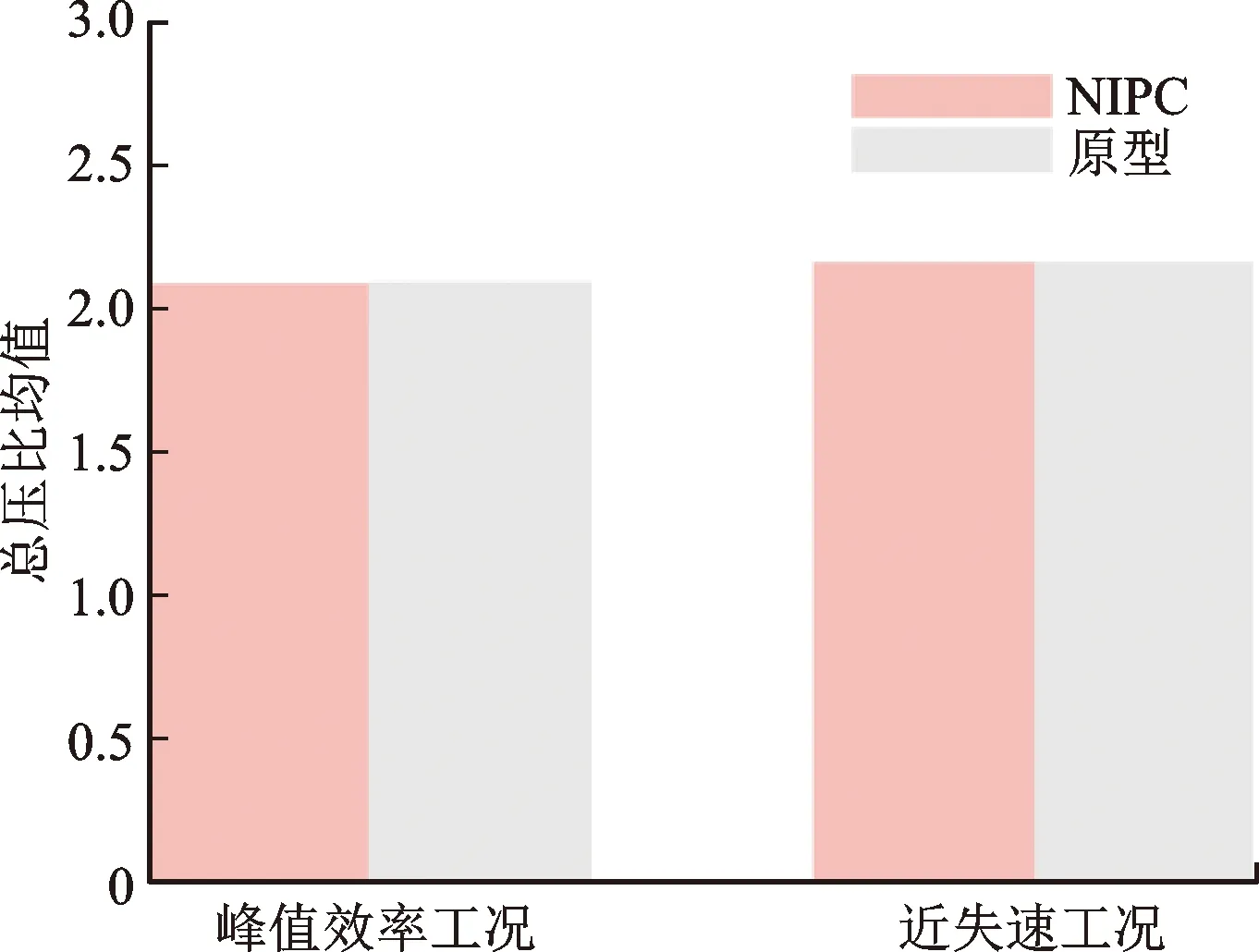
(b)总压比
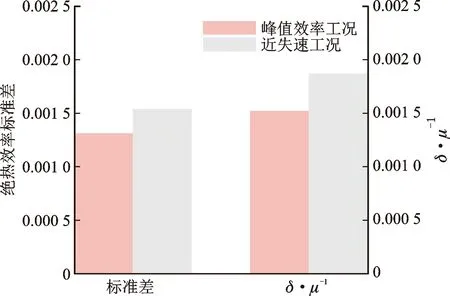
(a)绝热效率

(b)总压比
采用蒙特卡罗法在安装角偏差N(0,0.166 7)的概率空间内随机抽取100 000个样本,然后用NIPC所得模型预测这100 000个样本的输出响应,得到总压比和效率在峰值效率工况下概率分布,如图6所示。结果显示,总压比、绝热效率近似服从正态分布,而安装角偏差也服从正态分布,这说明了安装角偏差与峰值效率工况下的总压比和绝热效率的线性关系较好。

(a)总压比

(b)绝热效率
图7给出了近失速工况下性能参数的概率分布,发现总压比和绝热效率的分布与正态分布拟合效果良好,可见近失速工况下,总压比和绝热效率与安装角偏差的线性关系也较好。
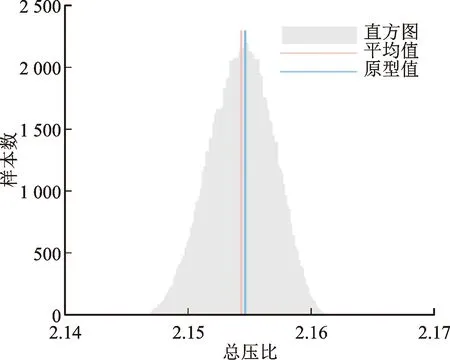
(a)总压比
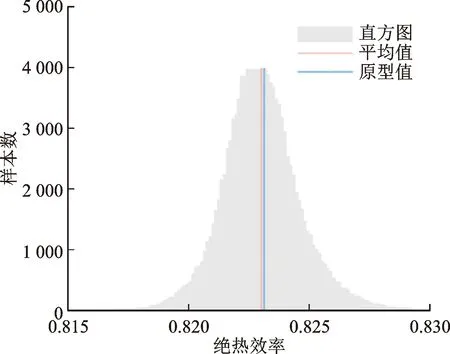
(b)绝热效率
观察图6和图7可知,安装角偏差使得平均气动参数产生了轻微下降。
3.2 相关性探讨
为证实上文提到的性能参数与安装角误差之间的线性关联性,引入Spearman和Pearson相关性分析,分别在两种工况下探讨安装角偏差与性能的相关性。
Spearman相关性分析对要分析的两个变量的分布不作要求,数据错误和异常值对Spearman相关性系数的影响很小。用于评估两个变量之间的单调相关性,在单调关系里,随着某一变量的增加,另一个变量也一起增加,但并不一定是随之线性增加。Spearman系数为1时,代表单调正相关,Spearman系数为-1时,代表单调负相关。相关系数的绝对值越接近于1,单调相关程度越强。Spearman系数ρS计算公式如下
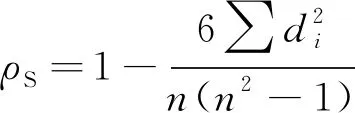
(13)
式中:d表示两变量排序后秩次差值;n表示样本数目;-1≤ρS≤1。
Pearson相关性分析用于评估两个连续变量之间是否具有线性关系,需要被分析的两个变量满足正态分布,异常值会对其结果造成很大的影响。Pearson系数取值为[-1,1],绝对值越大,线性相关程度越强,其值为1时,代表线性正相关。需要注意的是,当两个变量满足线性相关时,说明一定满足单调相关。当两个变量满足单调相关时,并不一定满足线性相关。Pearson系数ρ计算公式为
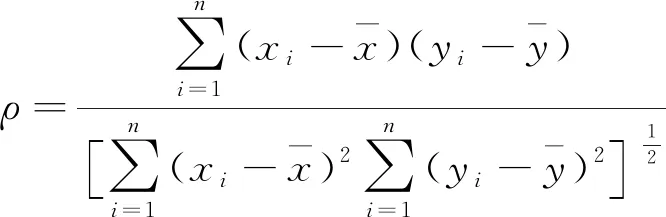
(14)
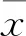
针对蒙特卡罗抽样生成的105个样本,运用Spearman相关性分析,得到输出与输入之间的相关性系数,结果如表4所示。从表中得知,两工况下总压比与安装角偏差呈单调正相关,绝热效率与安装角偏差呈单调负相关。

表4 安装角偏差与性能参数的Spearman系数
Pearson相关性分析要求被分析的两个变量服从正态分布。从图6和图7可知,PE工况和NS工况下总压比和绝热效率均近似服从正态分布,用自编写程序计算得到Pearson系数,结果如表5所示。在两工况下,总压比与安装角偏差呈较强线性正相关,绝热效率与安装角偏差呈较强线性负相关。

表5 安装角偏差与性能参数的Pearson系数
根据上文分析可知,两工况下总压比、绝热效率均与安装角偏差的线性关系较强。本文选用5阶非嵌入式多项式混沌方法,选取了6个误差点进行计算,最小二乘法拟合得到安装角偏差与峰值效率工况下绝热效率的线性函数关系式,如图8所示。函数关系式为y=-0.008 030 5x+0.861 435 8,x为安装角偏差,y为总压比,误差适用范围为-0.554 05°≤x≤0.554 05°。为检验该函数关系式的拟合精度,选取几个误差点,将NIPC模型的预估绝热效率和函数关系式的计算值进行对比,结果见图9,发现拟合精度较高,误差在0.05%以内。由此可见,该函数关系式在本文所研究的误差范围内能较为准确地反映安装角偏差与峰值效率工况下绝热效率的关系。
同理得到峰值效率工况下安装角偏差与总压比的函数关系式为y=0.052 289 6x+2.092 765 1, NIPC模型预估值与函数关系式计算结果之间误差在0.5%以内,误差较大。近失速工况下安装角偏差与绝热效率的函数关系式为y=-0.010 189 4x+0.823 104 7,误差在0.07%以内。近失速工况下安装角偏差与总压比的关系式为y=0.012 942 9x+2.154 191,误差在0.1%以内。
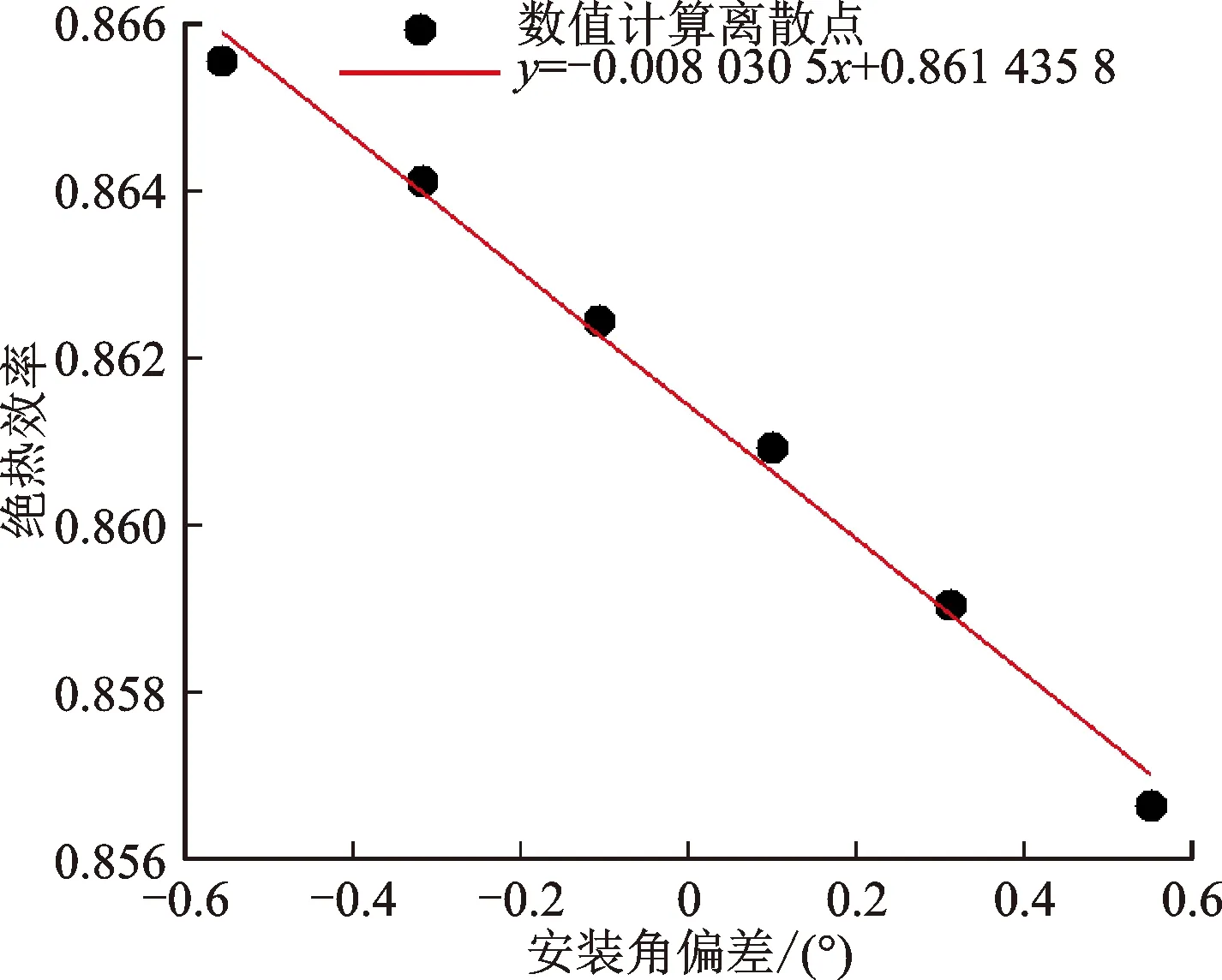
图8 安装角偏差与绝热效率的函数关系式Fig.8 The function relationship between stagger angle deviation and adiabatic efficiency

图9 绝热效率NIPC预估值与函数关系式计算值的对比 Fig.9 Comparison of NIPC predicted values and function formula
3.3 流场不确定性分析
图10展示了出口处绝热效率和总压比的无量纲标准差沿叶高的分布。从图10(a)看出,绝热效率无量纲标准差从叶根到叶顶呈现逐渐增加的趋势,两工况在95%~98%叶高范围内绝热效率的无量纲标准差均较大,说明这一区域的流场受安装角偏差的影响程度较大。从图10(b)看出,峰值效率工况下,总压比受安装角偏差不确定性的影响明显更大,且两工况下总压比的δ/μ在80%叶高以上的区域内较大。综合图10可以看出,安装角偏差的波动对叶顶区域的流场影响较大。下文将着重针对95%叶高截面的流场进行分析。
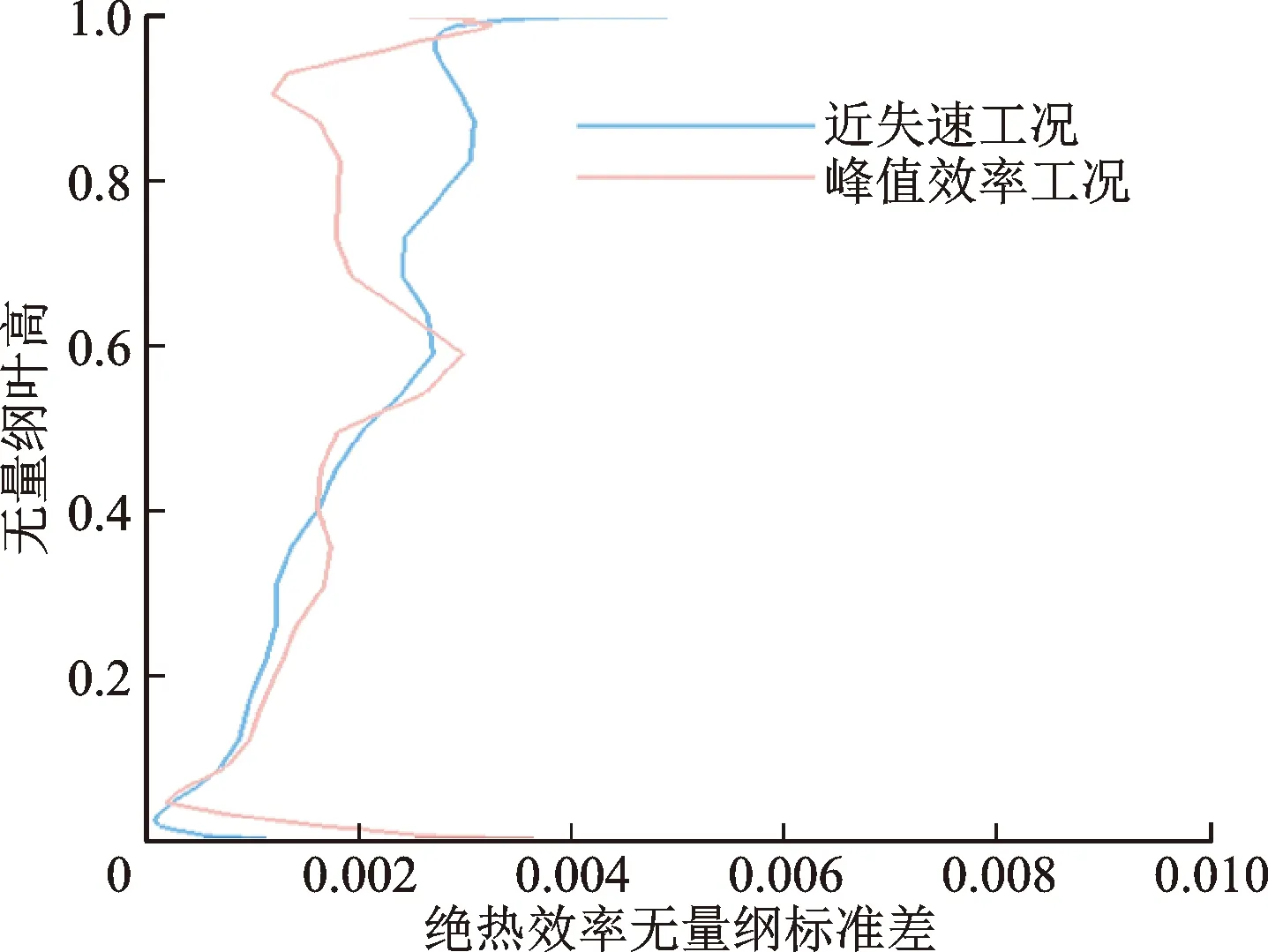
(a)绝热效率
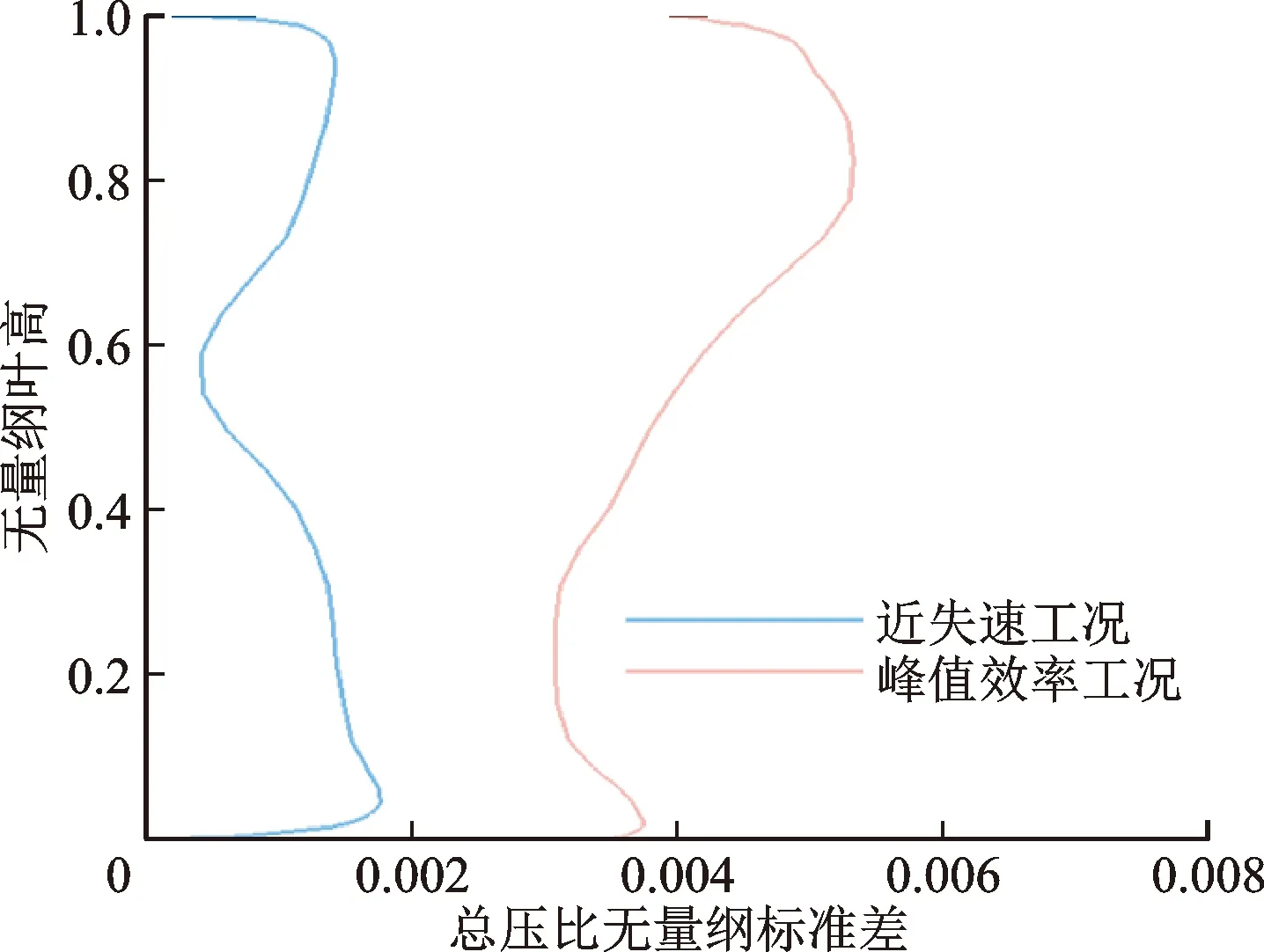
(b)总压比
静压系数可以用来评价转子的扩压能力,表示叶片表面某一点处的静压相对于进口平均静压的提升,定义如下

(15)

图11给出了95%叶高处两工况下静压系数的标准差沿无量纲轴向弦长的分布。标准差可以体现静压系数波动的幅度。NS工况下,压力面的静压系数标准差变化趋势非常平稳,吸力面在40%弦长位置处出现了一个波动峰值,该大幅度波动位置对应于激波位置,说明激波位置的流动受到显著不确定影响。PE工况下,静压系数在前缘出现较大幅度波动,说明前缘绕流加速段受到明显的不确定影响,吸力面在59%弦长位置处出现一个局部大幅度波动。对应于该位置处的激波,波动峰值大于NS工况处的静压系数波动幅度。峰值效率工况下,激波处的静压系数的波动幅度大约是近失速工况下的2.59倍。这说明,95%叶高处叶片表面扩压能力在峰值效率工况下受扰动影响更强烈。
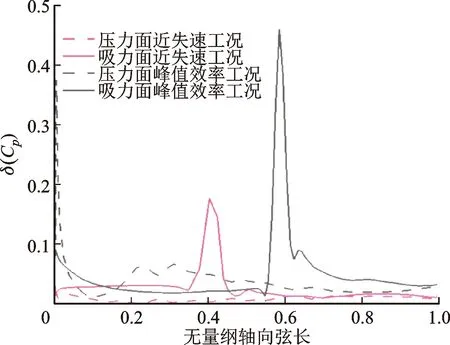
图11 95%叶高处静压系数标准差沿无量纲轴向弦长的分布 Fig.11 Distribution of δ(Cp) along dimensionless axial length at 95% span
相对马赫数的标准差可以体现流场受误差不确定性影响的程度,无量纲标准差越大,表明该位置处的相对马赫数波动程度越大,说明该位置处的流场对安装角误差波动越敏感。图12给出了95%叶高处相对马赫数无量纲标准差分布,从中发现,安装角误差不确定性主要对激波、叶尖泄漏流动、分离流动造成影响。两个工况下,相对马赫数标准差幅值较大的区域有所不同,峰值效率工况下,激波位置及波后叶尖间隙泄漏流动轨迹的δ/μ明显更大,该处流动受误差不确定性的影响程度较大。近失速工况下,马赫数的相对波动幅值最大的区域为间隙泄漏涡破碎区域和距离前缘40%弦长位置处出现的吸力面附面层分离流动,说明波后间隙泄漏涡破碎区域和吸力面附面层分离流动区域受安装角误差不确定性影响程度较大,对安装角不确定性较为敏感。峰值效率工况下,激波和分离流动区域的相对马赫数相对波动幅度达5%。近失速工况下,间隙泄漏涡破碎区域和激波引发的分离流动区域的相对马赫数的相对波动幅度达5%。

(a)峰值效率工况

(b)近失速工况
3.4 耗散函数分析
近失速工况下的损失受安装角不确定性的影响扰动更强,因此着重在NS工况下研究损失机理。高相对总压值的区域代表机械能损失累积的区域,是低速流聚集的区域,但它不能表示高损失源的分布[24]。为了分析流场中高损失区域出现的机理,引入耗散函数进行探讨。耗散函数将机械能转化为热能,可以评估生成的损失,耗散函数Ф定义如下
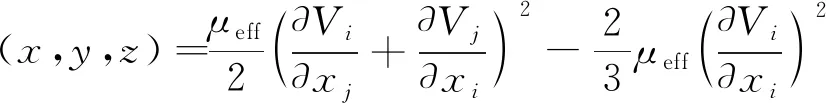
(16)
式中:Vi代表圆柱坐标系下气流相对速度的3个分速度;xi代表坐标轴3个方向的单位向量;考虑湍流黏性项μt后,动力黏度修正为μeff=(μ+μt)。
图13给出了近失速工况下耗散函数面积平均值的无量纲标准差沿无量纲轴向弦长的分布。从中可看出,前缘位置、40%弦长截面和尾缘位置截面的耗散函数的无量纲标准差较大,这些位置的损失受安装角误差不确定性影响程度较大。其中,尾缘位置截面耗散函数无量纲标准差最大,对安装角偏差的波动最为敏感。
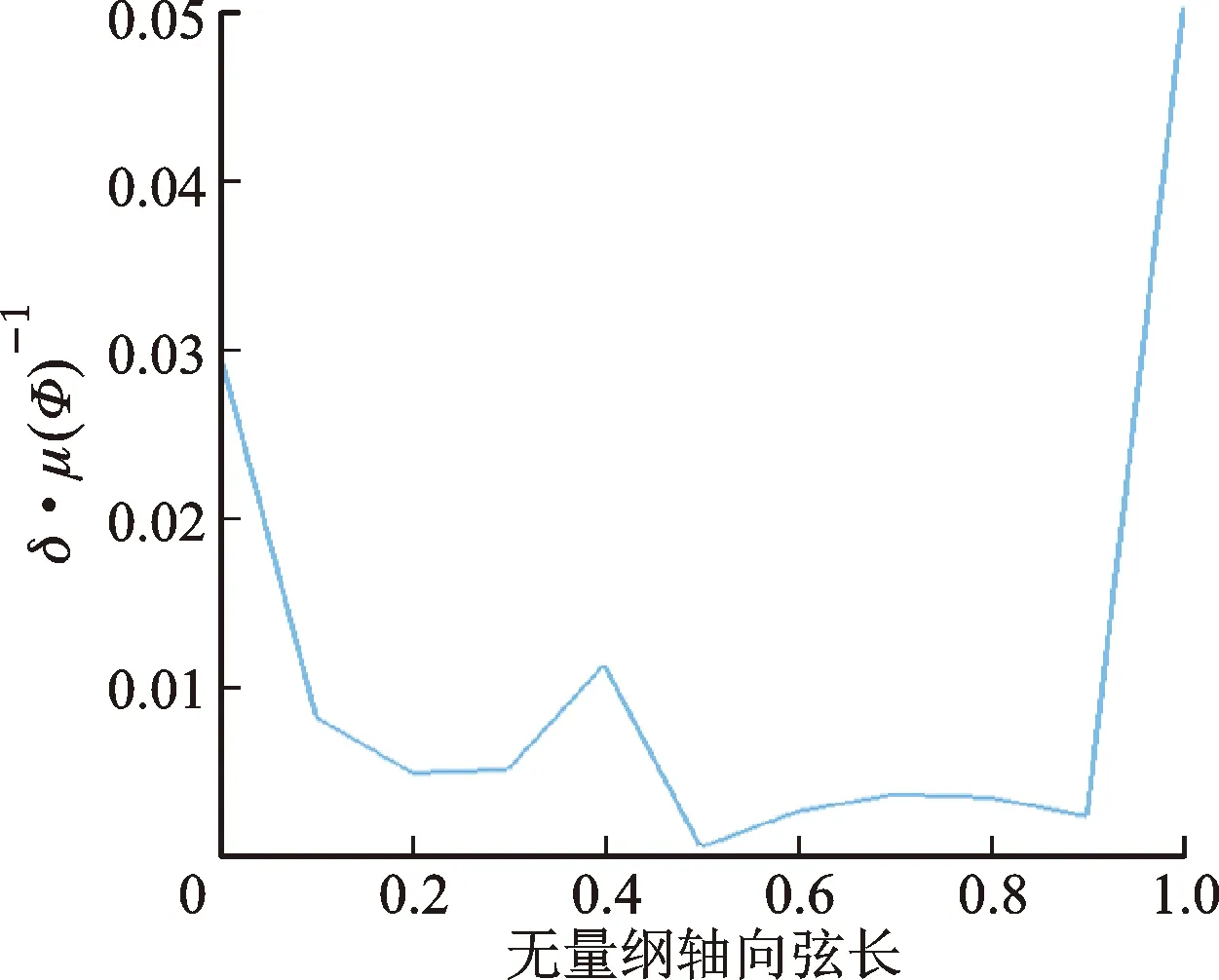
图13 耗散函数面积平均值的无量纲标准差沿弦长分布 Fig.13 Distribution of δ/μ(Φ) along dimensionless axial length
4 结 论
本文自主编制了非嵌入式混沌多项式(NIPC)程序,通过该不确定性量化方法,研究叶片安装角偏差对动叶的不确定性影响,分别在峰值效率工况和近失速工况下进行性能统计分析。采用Spearman和Pearson相关性分析,探讨各性能参数与安装角偏差间的相关程度,并通过流场分析,深入研究叶片安装角偏差波动对内部流场规律的影响,阐释气动性能不确定性的变化机理,可以得到以下结论。
(1)安装角偏差波动几乎不会对转子性能的平均水平造成影响,应该使用标准差和无量纲标准差来评估性能的波动程度。近失速工况下,绝热效率的相对波动幅度相比较峰值效率工况增加了22.95%,说明近失速工况下的损失受安装角不确定性的影响扰动更强。
(2)两种工况下总压比和绝热效率均近似服从正态分布。安装角偏差与总压比呈线性正相关,与绝热效率呈线性负相关,建立了安装角偏差与总压比和绝热效率的拟合关系式。
(3)峰值效率工况下,激波及波后叶尖间隙泄漏流动轨迹受误差不确定性的影响程度较大;近失速工况下,波后间隙泄漏涡破碎区域和吸力面附面层分离流动对安装角不确定性较为敏感,这些区域的流动是引起性能不确定性变化的主要原因。峰值效率工况下,激波和分离流动区域的相对马赫数波动幅度达5%。近失速工况下,间隙泄漏涡破碎区域和激波引发的分离流动区域的相对马赫数的波动幅度达5%。
(4)尾缘位置截面的耗散函数无量纲标准差值最大,说明尾缘处损失对安装角偏差的不确定性最为敏感。
