含海拔哑变量的杉木优势木高-树龄曲线模型研究

易 烜，黄 朗，朱晋梅，朱光玉，王琢玙，黄 靓

(1.湖南省青羊湖国有林场，湖南 宁乡 410627； 2.中南林业科技大学，湖南 长沙 410004； 3.湖南省生物多样性保护中心，湖南 长沙 410004)

立地质量是指某一立地上既定森林或其它植被类型的生产潜力，其随着树种的不同而变化[1]。立地质量评价是指针对立地的宜林性或潜在的生产力进行判断或预测[2]，是研究和掌握林分生长环境以及环境对林分生长影响的一个重要手段，是适树适地的理论依据，其目的是为收获预估而量化林地的生产潜力，或是为确定林分所属立地质量等级提供依据[2]。评价立地质量的方法和指标有很多，在人工林立地质量评价过程中，通常用立地指数来评价立地质量。

立地质量评价的指标主要包括林分高、蓄积量、指示植物和土壤等，在我国林业生产经营中已广泛应用，该套成熟的指标和方法主要适用于纯林或人工林[3-6]。Henriksen[7]采用既定年龄下的林分平均高用于评价阿拉斯加云杉(Piceaasperata)的立地生产力；林昌庚等[8]做过关于地位级表的研究工作；Perthuis等[9]提出18世纪立地指数的概念；Oettelt等[10]提出作为评价立地生产潜力的指标；Calamaa等[11]利用区域对立地指数曲线的影响，构建西班牙石松(Diaphasiastrumveitchii)纯林立地指数曲线。李希菲等[12]和段爱国等[13]研究了多型立地指数曲线。马炜等[14]采用相对优势高法编制了长白落叶松(Larixolgensis)人工林的立地指数表，并采用数式法编制了胸径地位级表；骆其邦[15]和朱光玉等[16]研究了南方杉木(Cunninghamialanceolata)和马尾松(Pinusmassoniana)立地指数转换关系。郭晋平等[17]对森林立地质量评价的可变生长截距模型与应用进行了研究。

杉木是我国长江流域、秦岭以南地区栽培最广、生长快、经济价值高的用材树种，早在明朝末年就开始较大规模的栽培人工林。根据第九次全国森林资源清查，我国现有营造的人工杉木林990.20万hm2，占全国人工乔木林面积的17.33%；蓄积量75545.01万m3，占蓄积比率22.30%，人工杉木面积、蓄积都位居全国人工乔木林第一[3]。本文以湖南省青羊湖、高泽源、江华等45个国有林场的杉木纯林数据为研究对象，采用多种常规的林木生长方程(非线性)，模拟、构建立地指数曲线模型，并对模型进行精度检验与对比分析；以最优模型为基础，考虑不同海拔对优势木高生长过程的影响，将海拔划分等级变量F，采用含哑变量(F)的回归分析方法，构建优势木高-树龄生长曲线，并对模型进行精度检验，分析模型的可行性，为区域性杉木立地质量评价提供建模依据。

1 研究区概况

湖南省属长江中下游云贵高原向江南丘陵和南岭山脉向江汉平原过渡的地带，地理位置界于24°38′—30°08′N，108°47′—114°15′ E之间，总面积21.18万m2。地势呈三面环山、朝北开口的马蹄形地貌，地跨长江、珠江两大水系，最高海拔为炎陵县境内的酃峰2115.2 m，最低海拔为长沙市岳麓区洋湖垸21.6 m。湖南省属大陆性亚热带季风气候，年平均气温16～19 ℃，年平均降水量在1 200～1700 mm。湖南省现有国有林场215个，属亚热带常绿阔叶林区，动植物资源丰富，是湘、资、沅、澧四水和大中型水库重要的生态屏障，保护着国家珍稀植物180多种，野生动物800多种。

2 研究方法

2.1 数据采集

采用典型取样的方法，在湖南青羊湖、高泽源、江华、黄丰桥、青石冈、五盖山、滁口、天鹅山、大坪、宋坪、月岩、金洞、荆竹山、大庙口、打鼓坪、五星岭、浆洞、水口山、罗溪、月溪、南洞、云马、东岭、武冈、寨市、龙山、排牙山、齐眉界、雪峰山、广坪、地连、高望界、石长溪、常德、大同山、花岩溪、塔市、五尖山、芦头、福寿山、浏阳湖、大熊山、弥泉、陈坪、拓溪等45个国有林场的人工杉木纯林中随机选取518个20 m×30 m的标准地，每块标准地内建立直角坐标系，对于胸径>5 cm 的林木记录其树种、树高、胸径、坐标等因子，对于胸径≤5 cm的幼树记录其树种、地径、树高、冠幅。选取其中388个标准地数据用作建立模型，130个标准地数据用作模型的适用性检验。建模及适用性检验数据来源见表1。

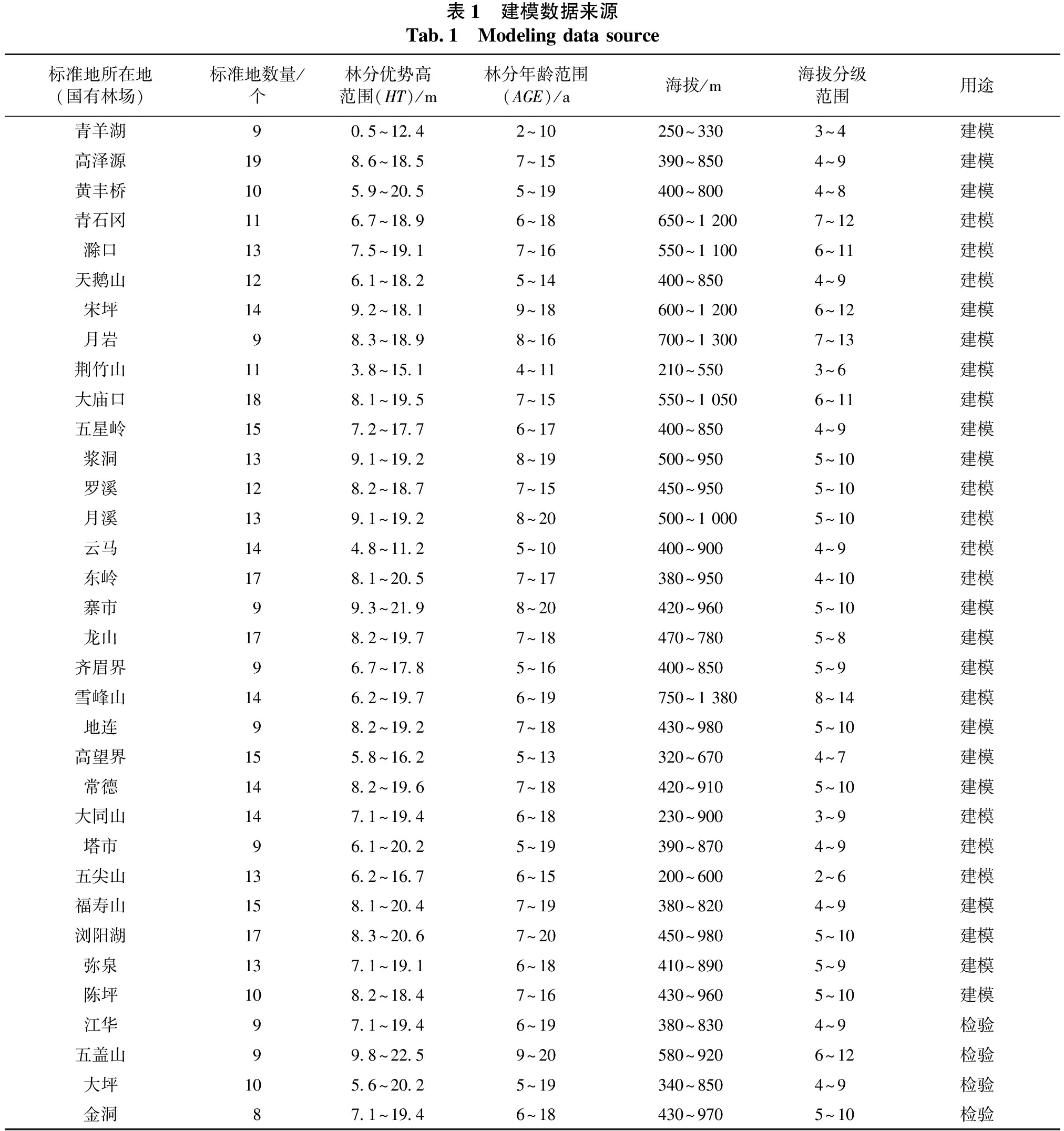
表1 建模数据来源Tab.1 Modeling data source标准地所在地(国有林场)标准地数量/个林分优势高范围(HT)/m林分年龄范围(AGE)/a海拔/m海拔分级范围用途青羊湖90.5～12.42～10250～3303～4建模高泽源198.6～18.57～15390～8504～9建模黄丰桥105.9～20.55～19400～8004～8建模青石冈116.7～18.96～18650～1 2007～12建模滁口137.5～19.17～16550～1 1006～11建模天鹅山126.1～18.25～14400～8504～9建模宋坪149.2～18.19～18600～1 2006～12建模月岩98.3～18.98～16700～1 3007～13建模荆竹山113.8～15.14～11210～5503～6建模大庙口188.1～19.57～15550～1 0506～11建模五星岭157.2～17.76～17400～8504～9建模浆洞139.1～19.28～19500～9505～10建模罗溪128.2～18.77～15450～9505～10建模月溪139.1～19.28～20500～1 0005～10建模云马144.8～11.25～10400～9004～9建模东岭178.1～20.57～17380～9504～10建模寨市99.3～21.98～20420～9605～10建模龙山178.2～19.77～18470～7805～8建模齐眉界96.7～17.85～16400～8505～9建模雪峰山146.2～19.76～19750～1 3808～14建模地连98.2～19.27～18430～9805～10建模高望界155.8～16.25～13320～6704～7建模常德148.2～19.67～18420～9105～10建模大同山147.1～19.46～18230～9003～9建模塔市96.1～20.25～19390～8704～9建模五尖山136.2～16.76～15200～6002～6建模福寿山158.1～20.47～19380～8204～9建模浏阳湖178.3～20.67～20450～9805～10建模弥泉137.1～19.16～18410～8905～9建模陈坪108.2～18.47～16430～9605～10建模江华97.1～19.46～19380～8304～9检验五盖山99.8～22.59～20580～9206～12检验大坪105.6～20.25～19340～8504～9检验金洞87.1～19.46～18430～9705～10检验

续表1 建模数据来源Continued Tab.1 Modeling data source标准地所在地(国有林场)标准地数量/个林分优势高范围(HT)/m林分年龄范围(AGE)/a海拔/m海拔分级范围用途打鼓坪98.9～18.27～17410～8905～9检验水口山87.3～22.46～20340～7804～8检验南洞117.9～19.17～18290～7203～8检验武冈87.5～19.86～19340～8904～9检验排牙山75.6～19.25～16450～8905～9检验广坪84.1～20.24～17230～6703～7检验石长溪96.9～18.26～17320～7804～8检验花岩溪75.1～17.25～15200～4002～4检验芦头118.8～21.59～20220～5903～6检验大熊山96.5～19.76～19270～8103～9检验拓溪75.6～16.25～14170～5302～6检验 注:海拔分级标准为100 m一个等级。

2.2 基础模型

采用理查德(Richards)、单分子式(Mitscherlich)和舒马切尔(Schumacher)等3种树木生长方程，利用ForStat(统计之林)数据分析软件，分别建立优势木高-树龄曲线模型，模型表达式见表 2，其中HT为林分优势高；a为优势高最大值；b与林木生长速度有关；c为形状参数；AGE为林分年龄。对模型进行精度检验与对比分析。

表2 模型的决定系数Tab.2 Determination coefficient of the model模型表达式RichardsHT=a×(1-e-b×AGE)cMitscherlichHT=a×eb/AGESchumacherHT=a×(1-b×e-c×AGE)

2.3 含哑变量模型

采用哑变量模型的方法构建杉木优势木高-树龄曲线模型。哑变量也称虚拟变量，通常取值为0、1。对研究区海拔进行分级的前提下，将分级后的海拔作为哑变量引入到杉木优势木高-树龄曲线模型的最优基础模型中，处理时，将变量赋值来表示定性或分类变量[1]，即：

(1)

i=1,2,…。

注: 当分类变量有n个水平,将其构建成哑变量时,考虑到变量间共线性问题,哑变量个数应为n-1个。

2.4 模型精度检验

采用决定系数、绝对残差均值和精度3个指标，利用ForStat(统计之林)数据分析软件，对模型精度进行检验。

决定系数：

(2)

平均绝对误差:

(3)

模型预估精度:

(4)

绝对残差均值越小，决定系数和精度越接近于1，则模型的模拟效果越好。

3 结果与分析

3.1 基础模拟模型筛选

采用Richards、Mitscherlich和Schumacher 3种常用的非线性基础模型方程，对林分平均优势木高与树龄的关系进行拟合分析(见表3)。对比3种模型的决定系数，结果表明，采用理查德(Richards)方程HT=a×(1-e-b×AGE)c建立的模型，模拟效果最好，决定系数达到0.794 89，故确定该模型为基础模拟模型。

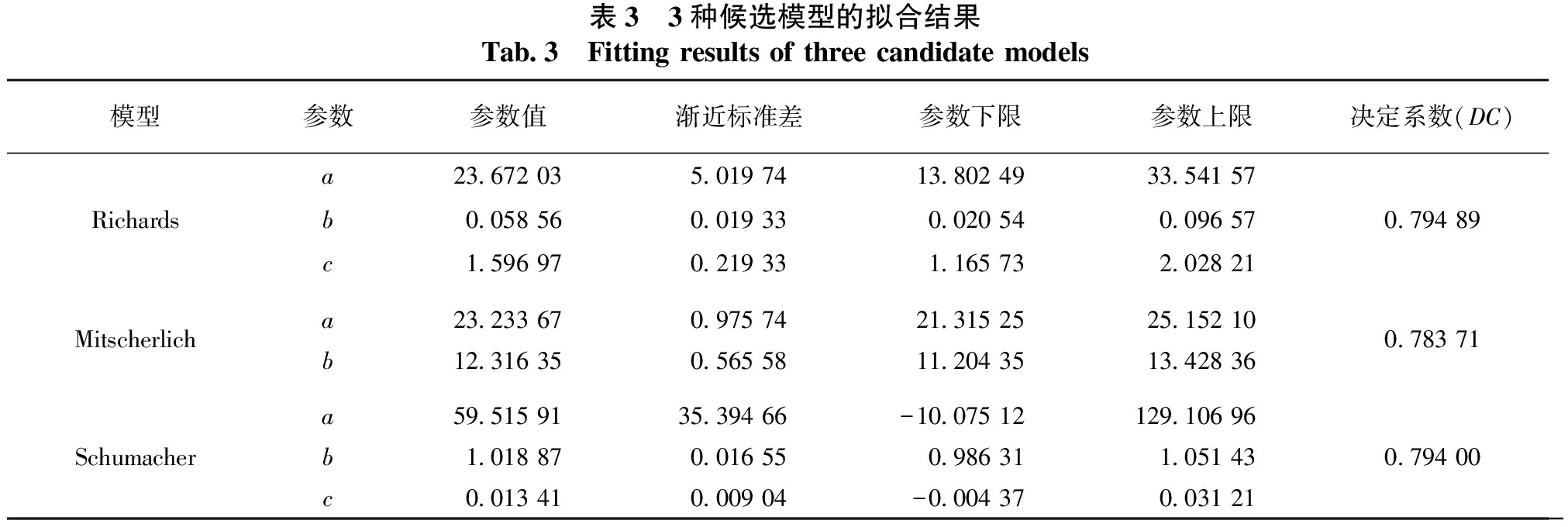
表3 3种候选模型的拟合结果Tab.3 Fitting results of three candidate models模型参数参数值渐近标准差参数下限参数上限决定系数(DC)a23.672 03 5.019 74 13.802 49 33.541 57 Richardsb0.058 56 0.019 33 0.020 54 0.096 57 0.794 89c1.596 97 0.219 33 1.165 73 2.028 21 Mitscherlicha23.233 67 0.975 74 21.315 25 25.152 100.783 71b12.316 35 0.565 58 11.204 35 13.428 36 a59.515 91 35.394 66 -10.075 12 129.106 96 Schumacherb1.018 87 0.016 55 0.986 31 1.051 43 0.794 00c0.013 41 0.009 04 -0.004 37 0.031 21

3.2 含哑变量(F)的优势木高-树龄生长曲线模型构建

确定基础模拟模型(Richards)后，以其为基础，纳入不同海拔对优势木高生长过程的影响，海拔以100 m为一个等级进行划分，将海拔等级变量(F)共划分为12个等级(见表1)，采用含哑变量的回归分析方法，构建优势木高-树龄生长曲线模型。含哑变量模型的表达式及其决定系数见表4。

表4 含哑变量模型的决定系数Tab.4 Determination coefficients of models with dummy variables模型表达式决定系数(DC)M1(F加在参数a上)HT(F)=(a,F)×(1-e-b×AGE)c0.843 52M2(F加在参数b上)HT(F)=a×(1-e-(b,F)×AGE)c0.844 41M3(F加在参数c上)HT(F)=a×(1-e-b×AGE)(c,F)0.842 80

由表4可知，含海拔哑变量模型M1(F加在参数a上)、M2(F加在参数b上)和M3(F加在参数c上)的决定系数分别为0.84352、0.844 41、0.84280，均大于Richards基础模型的决定系数0.79489(见表3)，表明加入哑变量(F)的模型所模拟的效果比不加哑变量(F)模型模拟的效果更好(见表5)。

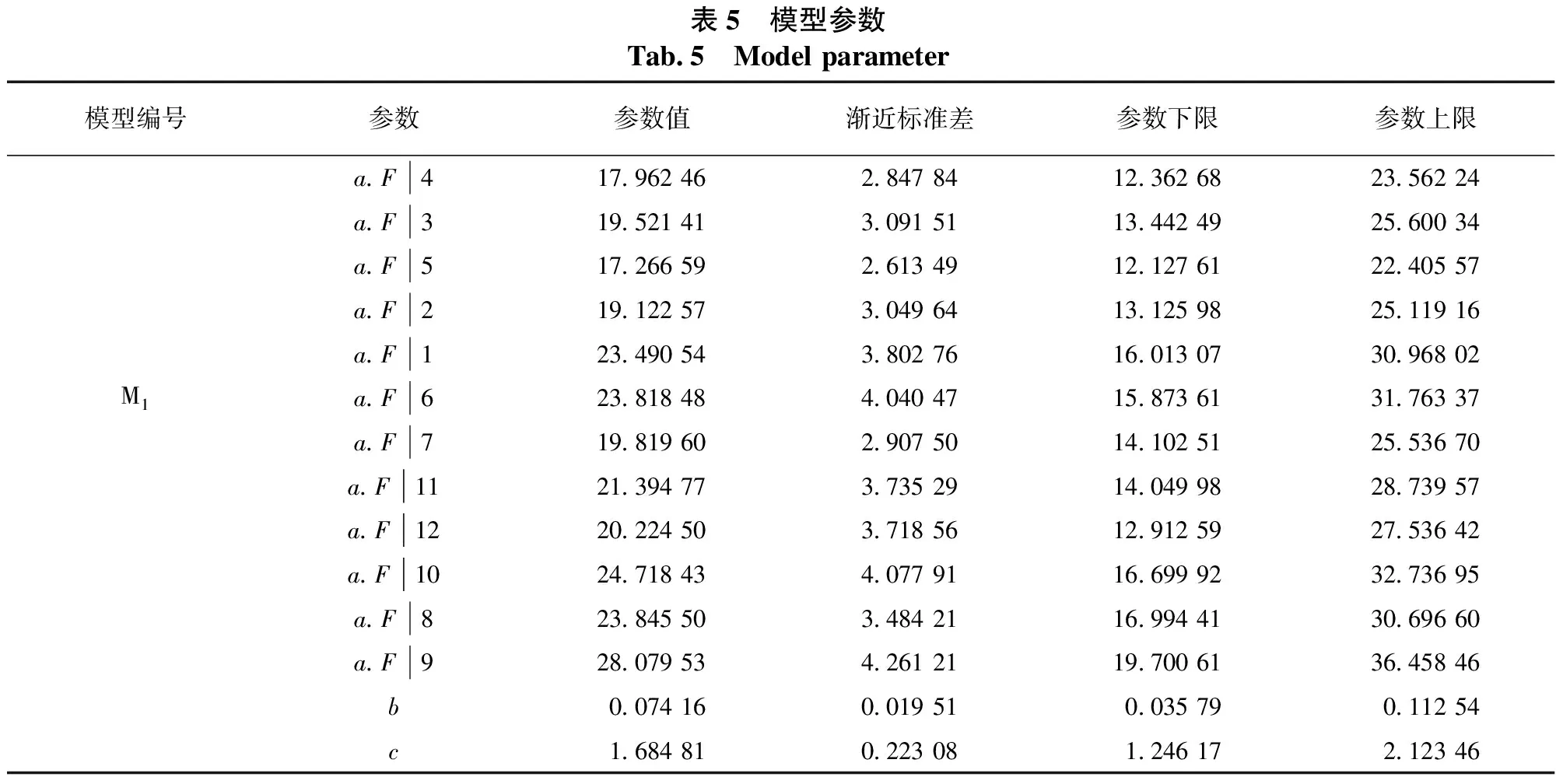
表5 模型参数Tab.5 Model parameter模型编号参数参数值渐近标准差参数下限参数上限a.F417.962 46 2.847 84 12.362 68 23.562 24a.F319.521 41 3.091 51 13.442 49 25.600 34a.F517.266 59 2.613 49 12.127 61 22.405 57a.F219.122 57 3.049 64 13.125 98 25.119 16a.F123.490 54 3.802 76 16.013 07 30.968 02M1a.F623.818 48 4.040 47 15.873 61 31.763 37a.F719.819 60 2.907 50 14.102 51 25.536 70a.F1121.394 77 3.735 29 14.049 98 28.739 57a.F1220.224 50 3.718 56 12.912 59 27.536 42a.F1024.718 43 4.077 91 16.699 92 32.736 95a.F823.845 50 3.484 21 16.994 41 30.696 60a.F928.079 53 4.261 21 19.700 61 36.458 46b0.074 16 0.019 51 0.035 79 0.112 54 c1.684 81 0.223 08 1.246 17 2.123 46

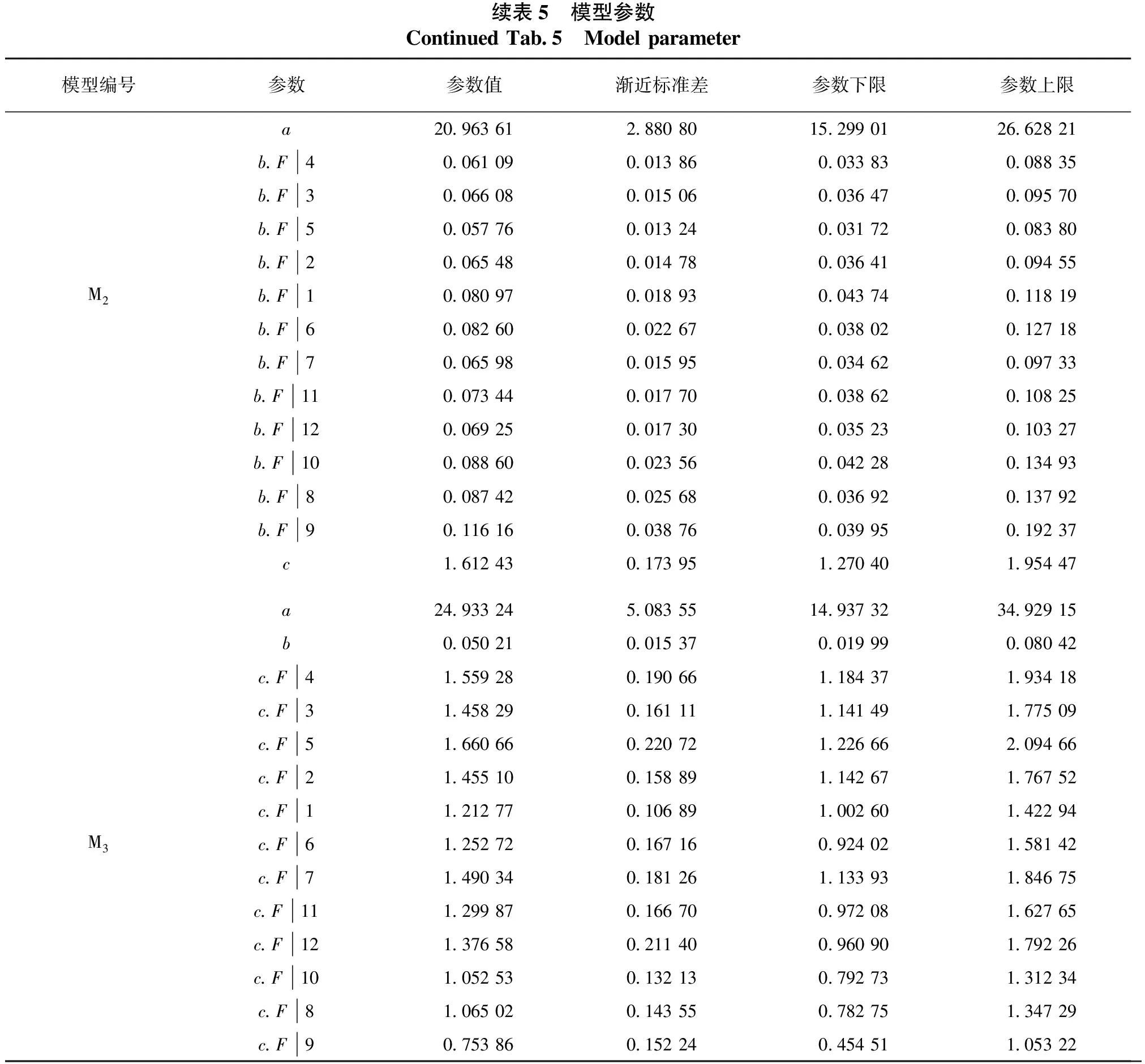
续表5 模型参数Continued Tab.5 Model parameter模型编号参数参数值渐近标准差参数下限参数上限a20.963 61 2.880 80 15.299 01 26.628 21b.F40.061 09 0.013 86 0.033 83 0.088 35b.F30.066 08 0.015 06 0.036 47 0.095 70b.F50.057 76 0.013 24 0.031 72 0.083 80b.F20.065 48 0.014 78 0.036 41 0.094 55M2b.F10.080 97 0.018 93 0.043 74 0.118 19b.F60.082 60 0.022 67 0.038 02 0.127 18b.F70.065 98 0.015 95 0.034 62 0.097 33b.F110.073 44 0.017 70 0.038 62 0.108 25b.F120.069 25 0.017 30 0.035 23 0.103 27b.F100.088 60 0.023 56 0.042 28 0.134 93b.F80.087 42 0.025 68 0.036 92 0.137 92b.F90.116 16 0.038 76 0.039 95 0.192 37c1.612 43 0.173 95 1.270 40 1.954 47a24.933 24 5.083 55 14.937 32 34.929 15b0.050 21 0.015 37 0.019 99 0.080 42c.F41.559 28 0.190 66 1.184 37 1.934 18c.F31.458 29 0.161 11 1.141 49 1.775 09c.F51.660 66 0.220 72 1.226 66 2.094 66c.F21.455 10 0.158 89 1.142 67 1.767 52c.F11.212 77 0.106 89 1.002 60 1.422 94M3c.F61.252 72 0.167 16 0.924 02 1.581 42c.F71.490 34 0.181 26 1.133 93 1.846 75c.F111.299 87 0.166 70 0.972 08 1.627 65c.F121.376 58 0.211 40 0.960 90 1.792 26c.F101.052 53 0.132 13 0.792 73 1.312 34c.F81.065 02 0.143 55 0.782 75 1.347 29 c.F90.753 86 0.152 24 0.454 51 1.053 22

3.3 模型精度检验

由表6可知，常规非线性Richards基础模型的绝对残差均值、决定系数、模型精度分别为1.412 85、0.794 89和97.39%。加入以海拔等级为哑变量的M1模型分别为1.207 33、0.843 52、97.66%，M2模型分别为1.206 30、0.844 41、97.77%，M3模型分别为1.227 21、0.842 80、97.75%。加入以海拔等级为哑变量的M1、M2和M3模型的绝对残差均值都小于常规非线性Richards基础模型的绝对残差均值；模型M1、M2和M3的决定系数与模型精度更接近于1，且均大于常规非线性Richards基础模型。

由于绝对残差均值越小，决定系数和精度越接近于1，则模型的模拟效果越好。因此，加入以海拔等级为哑变量的M1、M2和M3模型的精度要优于常规的非线性基础模型，其中以模型M2最优。

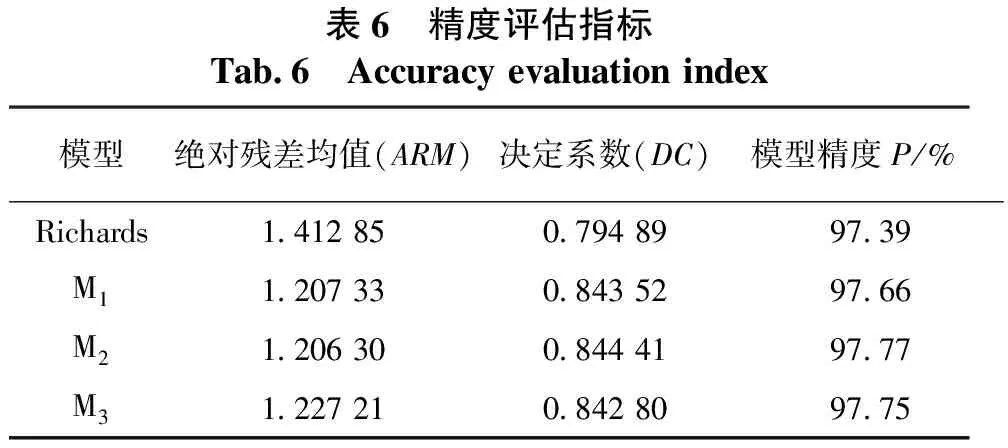
表6 精度评估指标Tab.6 Accuracy evaluation index模型绝对残差均值(ARM)决定系数(DC)模型精度P/%Richards1.412 850.794 8997.39M11.207 330.843 5297.66M21.206 300.844 4197.77M31.227 21 0.842 8097.75

3.4 模型适用性检验

130个杉木纯林标准地数据模型M2的残差分析结果见表7，其制作残差分布图见图1，以此进行适用性检验。

表7 模型适用性检验Tab.7 The model adaptability testHTHT预测值(F加在b上)残差0.500.712 18-0.212 180.500.722 06-0.222 060.600.720 27-0.120 270.750.588 840.161 150.900.978 63-0.078 63…8.7010.373 93-1.673 938.8010.447 57-1.647 579.109.793 32-0.693 329.1511.390 17-2.240 179.207.486 731.713 26…17.0015.950 871.049 1217.4012.763 654.636 3417.9010.363 997.536 0018.4018.095 150.304 84

图1 残差分布Fig.1 Residual distribution

从图1可知，模型M2(F加在参数b上)的残差值在横轴上下大致呈对称均匀分布，经计算其残差均值为-0.115 01，模型M2的适用性检验效果较好。

4 结论与讨论

(1)通过Richards、Mitscherlich和Schumacher 3种导向曲线模型构建和精度分析，筛选出最优的杉木优势木高与树龄Richards基础方程：HT=a×(1-e-b×AGE)c，其决定系数为0.794 89。

(2)以100 m为一个等级，将研究区内海拔分为12个等级，构建海拔分级变量(F)，通过含哑变量(海拔分级变量)的回归分析，对杉木平均优势木高与树龄的相关关系进行模拟。其结果含海拔哑变量F加在参数a、b和c上得到的决定系数分别为0.843 52、0.844 41、0.842 80，均大于Richards基础模型的决定系数0.794 89，以哑变量加在参数b上最优，其绝对残差均值为1.206 30，模型精度达97.77%。对最优模拟模型进行适应性检验，其残差均值为-0.115 01，残差均匀分布在预测值两侧，可作为湖南省杉木平均优势木高与树龄的关连的预测。

(3)与常用的线性或非线性回归模型相比，含哑变量模型通常能够更精确的反映树木生长受到的树种结构、立地条件等其他条件的影响，展现出不同立地条件下树木生长的差异，基于此特点的含哑变量回归模型已广泛应用于林业模型的构建[19]。王君杰等[20]以大兴安岭兴安落叶松(Larixgmelinii)为研究对象，构建了含区域哑变量的树高-胸径模型，发现含区域哑变量的模型精度要高于基础模型。Sharma等[21]基于捷克国家连续清查数据，将描述物种差异性、冠层差异性的哑变量纳入高径比模型，提高了模型的精度。可以看出，与传统的理论基础模型相比，构建含哑变量的模型能够有效的提升模型精度与适用性。考虑到湖南省地处丘陵地带，地形地貌复杂，海拔差异明显，对杉木生长有着显著影响，通过对研究区海拔进行分级，将其作为哑变量，构建了含海拔哑变量的杉木优势木高-树龄曲线模型，能明显的提升模型精度，这与康立[22]的研究结论一致，为区域性杉木人工林优势木高-树龄曲线模型的构建以及立地质量评价提供了一种有效的思路与途径。