激光追踪测量系统机械结构模态参数影响
2023-05-04陈洪芳郭治博李长亮宋辉旭石照耀
陈洪芳, 郭治博, 李长亮, 宋辉旭, 石照耀
(1.北京工业大学 材料与制造学部,北京 100124;2.北京工业大学 北京市精密测控技术与仪器工程技术研究中心, 北京 100124)
激光跟踪测量系统是在工业测量系统中的一种高精度、高可靠性、大尺寸测量系统,应用激光跟踪测量系统的仪器主要有激光跟踪仪和激光追踪仪,激光跟踪仪可实现在球坐标系下的测角测距,挡光或者断光后不可再续;具有高精度、高效率、实时跟踪的测量优点,适合大尺寸工件装配测量。激光追踪仪不涉及旋转角度的测量,并且激光追踪仪选用位置固定且不参与运动的标准球作反射机构,使误差源引入最少,提高了空间测量的效率和精度。激光追踪测量系统的机械结构是整个激光追踪测量系统的硬件平台,其结构设计的优良直接关系到整个测量系统的精度,机械结构首先是控制系统的执行端,在可编程多轴控制器(programmable multi-axes controller,PMAC)运动控制系统的控制下,进行两轴运动达到对目标靶镜的追踪,其次机械结构还集成了光学系统和激光干涉信号采集系统,因此,对激光追踪测量系统机械结构的研究与分析具有重要意义[1-2]。
模态分析是一种研究机械结构的方法,通过模态分析方法可以分析机械结构在某一个易受影响的频率范围内各阶主要模态的特性,进而给出机械结构在此频段内外部或内部各种振动源作用下实际响应[3-11]。Er等[3]提出了一种使用基于频率响应函数的实验模态分析进行机器振动分析的方法。该方法的优势是根据对机器模型进行的有限元分析的结果进行评估的。Jannifar[4]提出使用完善的时间同步平均技术与开发的自动驾驶冲击系统相结合,在运行谐波中执行实验模态分析。刘琳琳等[5]提出了三维针刺废棉纤维/环氧树脂复合材料的小尺寸微观结构模型,以有限元分析方法预测其关键振动参数(固有频率和振型),通过实验模态分析方法进行了测试,以验证有限元方法对固有频率和模态振型预测的准确性。曹儿芳等[6]基于其自行研发的飞秒激光精密跟踪转盘进行相关研究,总结了转台固有频率与刚度特性,摩擦和转动惯量之间的关系,确定了结构材料的特性,为激光精密跟踪转台结构的小型化和轻量化提供了有效的改进措施,但是其只做了有限元模态分析并未进行试验模态实验。
本文基于自主设计的激光追踪测量机械系统,提出一种分析激光追踪测量系统机械结构模态参数影响的方法,以提高机械系统的精度。
1 激光追踪测量系统机械结构
激光追踪测量系统机械结构主要由底座、两精密转轴轴系和2个伺服减速电机、光学系统支撑板和光学元件以及标准球调节座组成,如图1(a)所示[7]。回转轴轴系包括回转轴电机和回转轴轴系微调支撑板,回转轴轴系将整个俯仰轴部分作为负载进行工作。俯仰轴轴系运转光学系统平台,俯仰轴轴系主要包括俯仰轴电机和俯仰轴支撑架,通过水平轴系微调连接板与光学平台紧密相连。光学平台主要用来布置光学元件和激光干涉信号接收器以及位置敏感探测器。激光追踪测量系统的机械结构的性能和动态特性以及机械结构的参数都会影响测量系统的准确度和精确度。
对完整激光追踪测量系统进行动力学以及力学分析的过程较为复杂,存在许多非关键部件,如果在有限元模型中包含这些特征,就必须对这些区域划分极细小的网格,不仅过程复杂还对结果造成较大的影响,需对其进行简化处理。去除与结构无关的外购件标准球、光学仪器、防尘壳、细小结构螺纹和垫圈等,得到如图1(b)所示的激光追踪测量系统机械结构的简化模型。本文将基于此简化模型,基于有限元法的模态分析理论,对结构材料密度、弹性模量和不同材料对系统固有频率的影响进行分析。
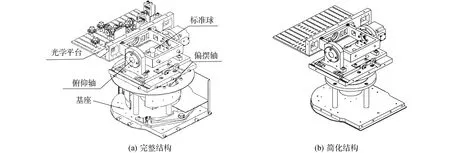
图1 激光追踪测量系统机械结构Fig.1 Schematic picture of laser tracer measurement system
2 机械系统模态分析
模态分析是分析结构固有频率和模态振型的主要方法[12]。线性多自由度系统可以分解为N个单自由度子系统。系统的频率响应函数是每个单自由度子系统的频率响应函数的加权和:
(1)
式中:Mi表示系统质量矩阵;Ki表示系统刚度矩阵;Ci表示系统阻尼矩阵;φi为频率矩阵;ω为振动角频率。
系统结构的频率响应函数矩阵的每一行或每一列都包含结构系统的所有模态参数,模态测试的基本原理是通过获得频率响应来获得结构的模态参数。
在有限元分析的基础上,结构整体运动方程为:
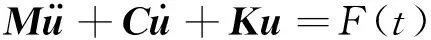
(2)
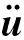
在无阻尼振动系统中,激光追踪测量系统机械结构基于有限个特征单元,结构的刚度和质量都保持恒定,结构的振动方程为:
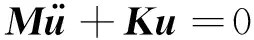
(3)
其中,刚度矩阵可以包括预应力效应带来的附加刚度,对于线性系统,自由振动满足:
{u}={φi}cos(ωit)
(4)
式中:{φi}表示第i阶模态形状的特征向量;ωi表示第i阶固有振动角频率为:
(5)
则第i阶固有频率为:
(6)
3 激光追踪测量系统机械结构模态仿真实验
完整激光追踪测量系统进行模态分析过程较为复杂,存在很多影响较小处理复杂的部件需进行简化处理,如图2为所示激光追踪测量系统机械结构的有限元模型。
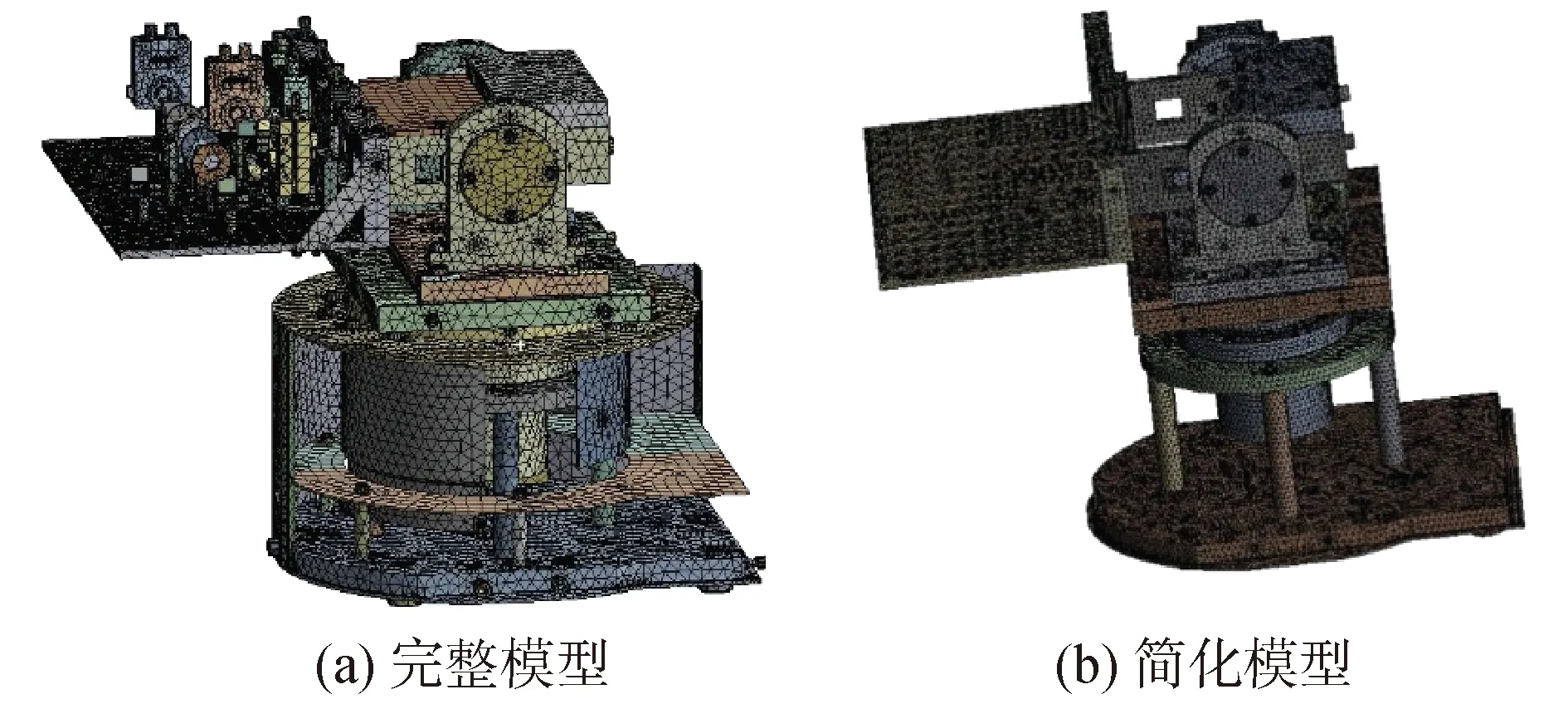
图2 激光追踪测量系统机械结构有限元模型Fig.2 Finite element models of mechanical structure of laser tracing measurement system
3.1 机械结构的计算模态仿真
在ANSYS Workbench中创建modal分析项目,将三维模型导入到项目工程中定义材料数据,选择的主要材料为45#结构钢和模具钢H13,定义各部件的连接方式。由于低阶模态对机械结构工作过程中影响比较大,在modal选项中的Analysis Settings中设置分析前6阶模态,利用Total Deformation求解器查看各阶模态固有频率和振型,结果如图3所示。
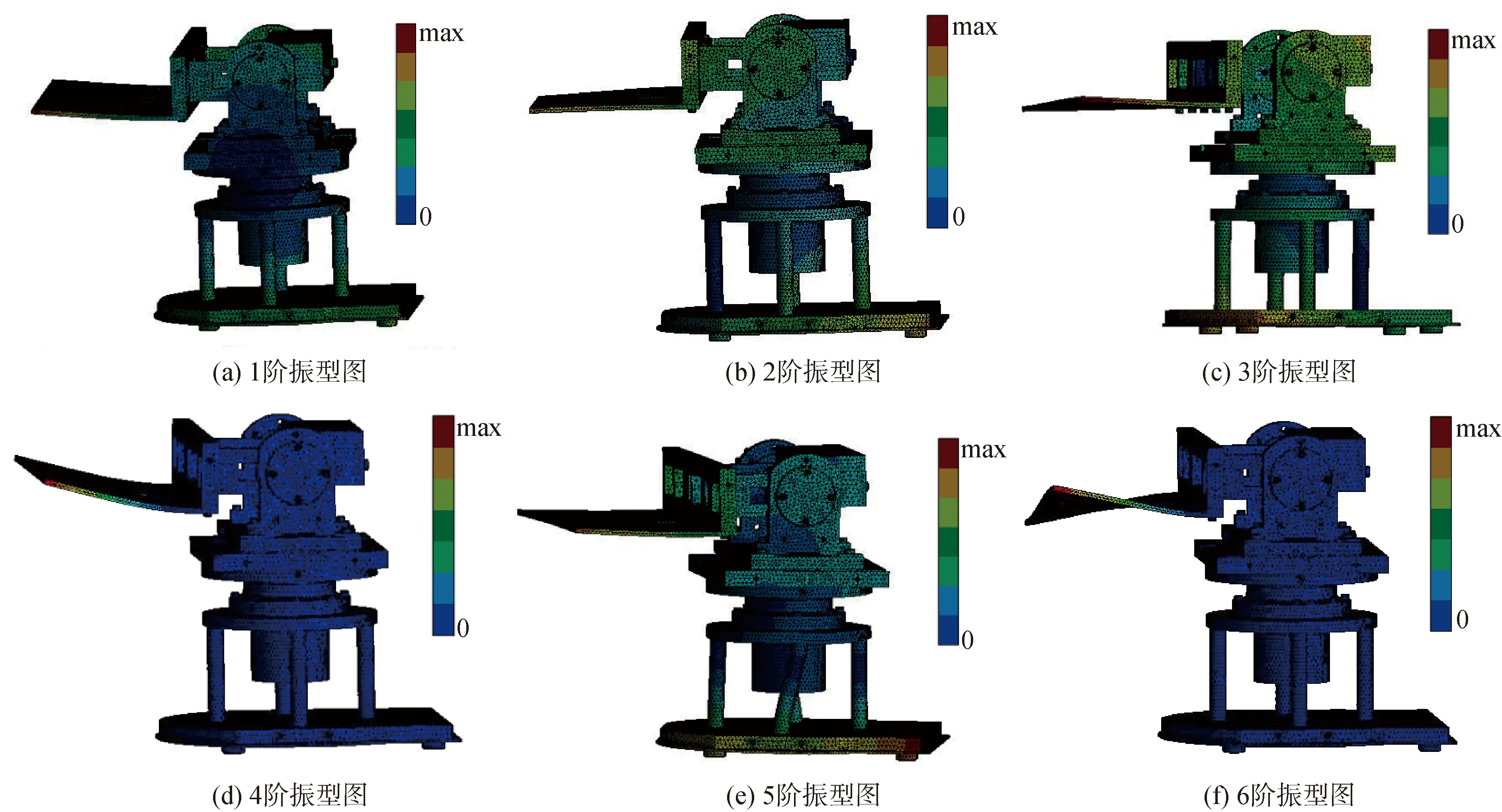
图3 激光追踪测量系统机械结构前6阶模态振型图Fig.3 The 6 modes of the mechanical structure of the laser tracer measurement system
激光追踪测量系统机械结构前6阶固有频率值分别为69.921,91.416,121.46,186.52,220.67,319.59 Hz,其固有频率值随阶数的增加而增大。
图3(a)和(b)为结构的1阶振型和2阶振型,结构变形较为不明显主要是光学底板的变形;图3(c)和(d)为结构固有频率在121.46、186.52 Hz时的3阶、4阶振型,主要是结构光学底板发生上下变形和扭转变形时的受力振型,变形同样集中在光学底板上;图3(e)和(f)为结构固有频率在220.67和319.59 Hz时的5、6阶振型,主要是机械结构扭转变形,集中在光学底板和底部支撑的4个立柱上,可以看到振动较为强烈的部分主要集中在光学底板和底部支撑立柱上面。
3.2 材料密度对系统固有频率影响分析
保持激光追踪测量系统机械机构的尺寸和结构材料参数不变,只改变材料的密度来模拟不同的结构质量参数。在实际结构选用材料结构钢的基础上分别改变密度值获取了10组模型进行了模态分析获得结构固有频率与材料密度即质量或惯量之间的数据如图4所示所示,材料密度的改变也即质量的改变会引起激光追踪测量系统机械结构固有频率的改变,随着结构密度的增大机械结构的固有频率逐渐减小;结构密度改变对不同阶固有频率的影响效果不同,相同密度参数变化率下,高阶频率的变化幅度较大。
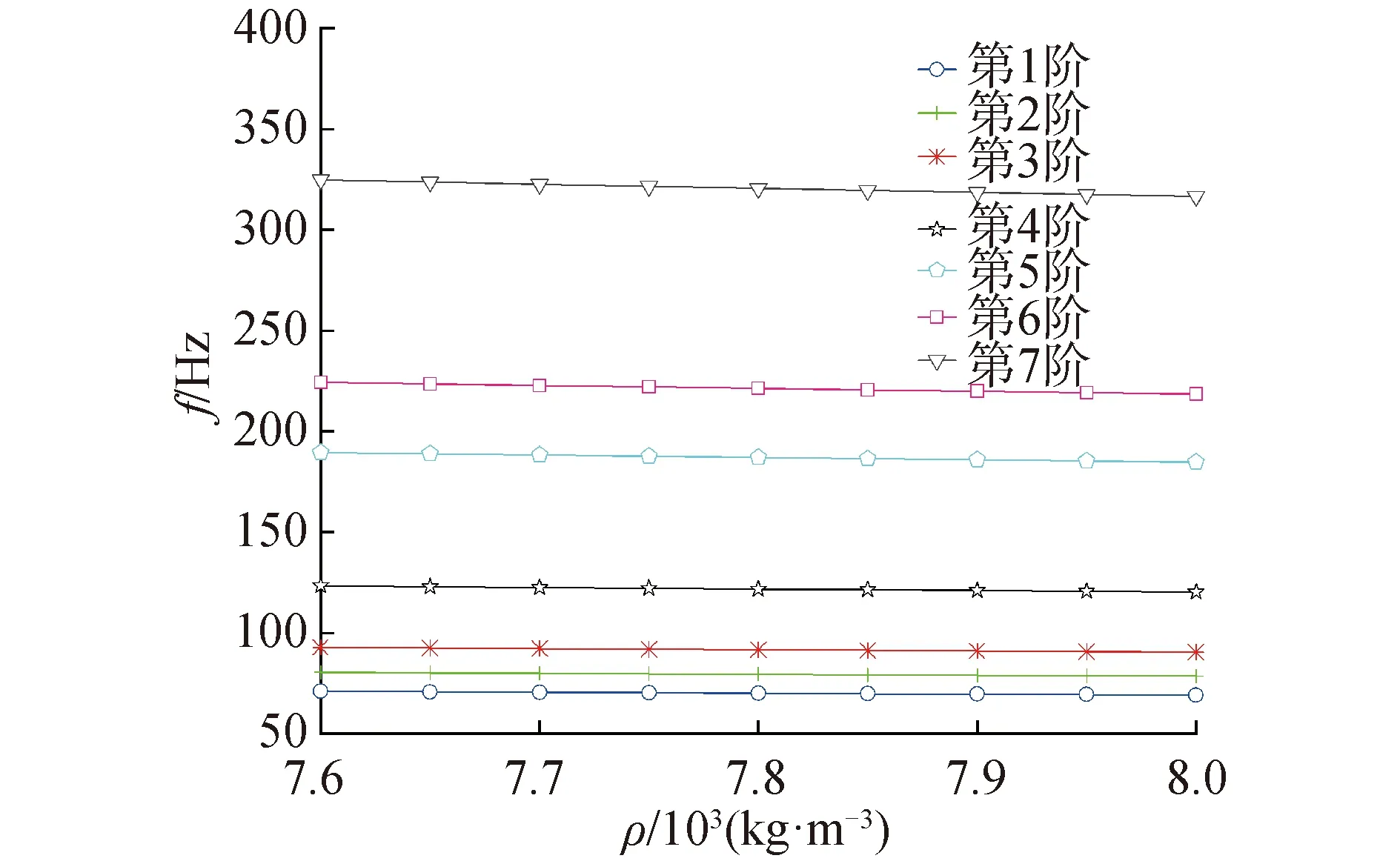
图4 材料密度与结构固有频率关系曲线Fig.4 Diagrams of material density and natural frequency of structure
3.3 弹性模量对系统固有频率影响分析
刚度特性是指材料或结构在受力时抵抗弹性变形的能力,弹性模量越大,材料刚性越好,抵抗弹性变形的能力越强。通过控制结构的材料密度、泊松比等参数不变,仅改变材料弹性模量数值,对结构进行模态分析。由图5弹性模量与结构固有频率关系曲线可知,随着结构材料刚度的增加激光追踪测量系统机械结构的固有频率逐步增大,弹性模量对结构固有频率的影响随着固有频率的阶数增加而逐渐增加。
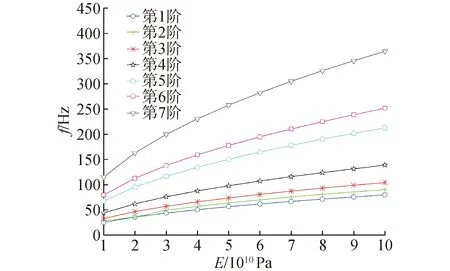
图5 弹性模量与结构固有频率关系曲线Fig.5 Diagrams of material elasticity and natural frequency of structure
3.4 不同材料对系统固有频率影响分析
不同材料之间有着不同的属性,仿真研究了不同材料下激光追踪测量系统机械结构固有频率的影响。由图6不同材料与结构固有频率的关系曲线可以看出,不同材料之间的固有频率值有明显的不同,从分析的5种常用材料发现,铝合金、镁合金和45#钢的前7阶固有频率变化趋势一致且大小相近,在满足强度条件下,就结构固有频率而言,铝合金材料密度相对较小且弹性模量大,可以作为激光追踪测量系统机械结构优先考虑选用的材料。
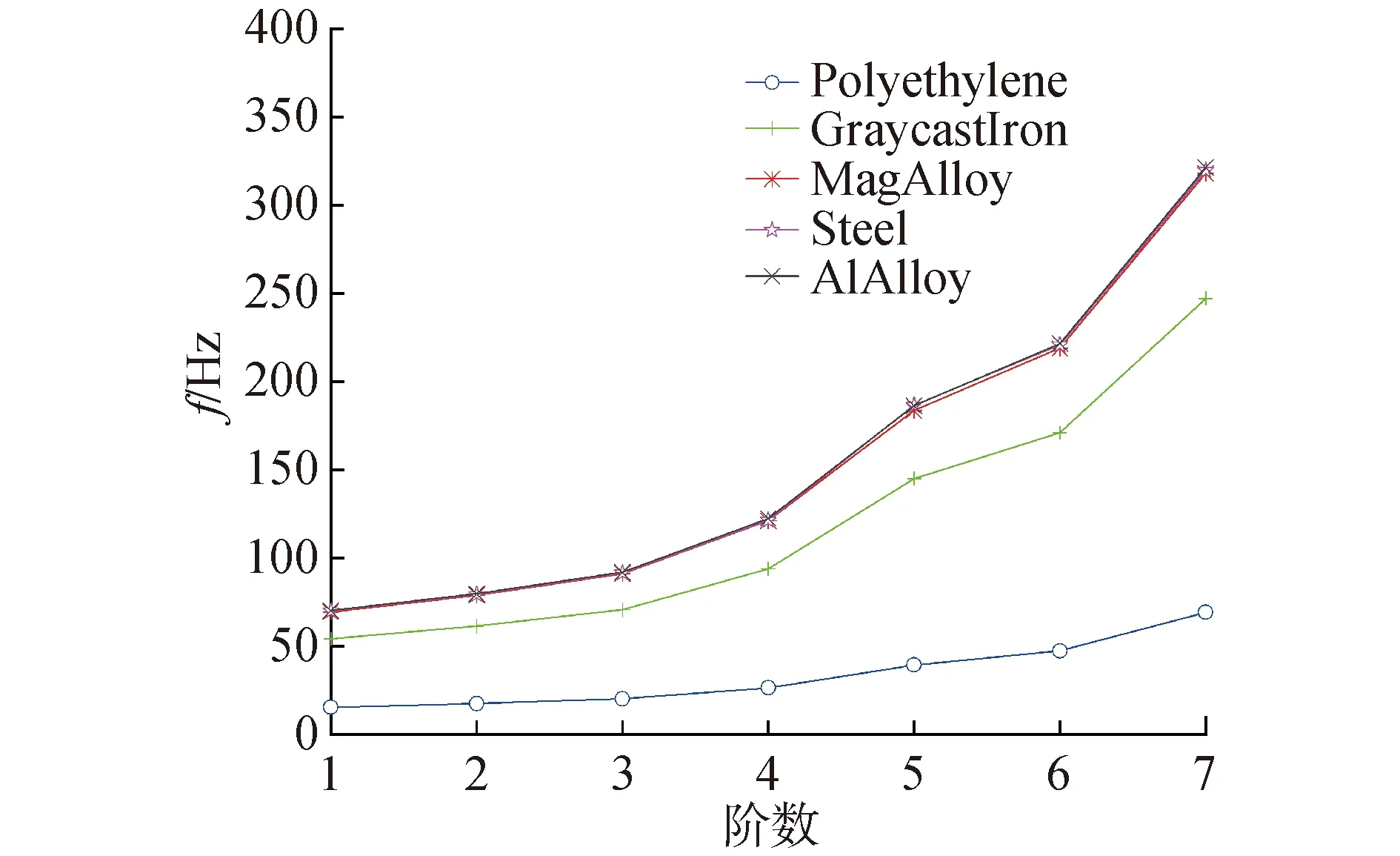
图6 不同材料与结构固有频率关系曲线Fig.6 Diagrams of material elasticity and natural frequency of structure
4 激光追踪测量系统机械结构模态实验
进行模态试验的对象是材料为45#结构钢的激光追踪测量系统,该材料弹性模量大,材料刚性好,抵抗弹性变形的能力强,可以减少由弹性变形引起的误差,相较于其他材料低成本和易获取。
通过试验模态实验,可以得到激光追踪测量系统机械结构的固有频率、阻尼、模态振型,为激光追踪测量系统的振动特性分析,振动故障诊断和预报以及结构动力特性的优化设计提供依据。实验模态分析的流程如图7所示,北京东方振动和噪声技术研究所的DASP V11软件进行结构生成。
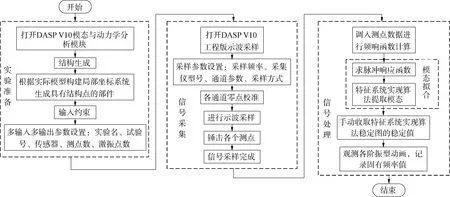
图7 实验模态分析流程Fig.7 Experimental modal analysis process
使用北京东方振动和噪声技术研究所的INV3020C仪器对激光追踪测量系统进行激振实验,对采集的振动信号数据进行处理识别从而得到机械系统的模态参数。通过对采样数据进行频响函数分析,并计算脉冲响应函数,用特征系统实现算法进行模态拟合。
通过脉冲响应函数进行特征系统实现算法,得到除模态频率、阻尼和振型外,也可得到模态质量和刚度,当模态频率较密集,频域法识别有难度时,将频响函数逆变换得到脉冲响应函数,用特征系统实现算法进行识别,对稳定点多的结构手动提取稳定模态,经实验模态分析观测模态振型如图8所示。
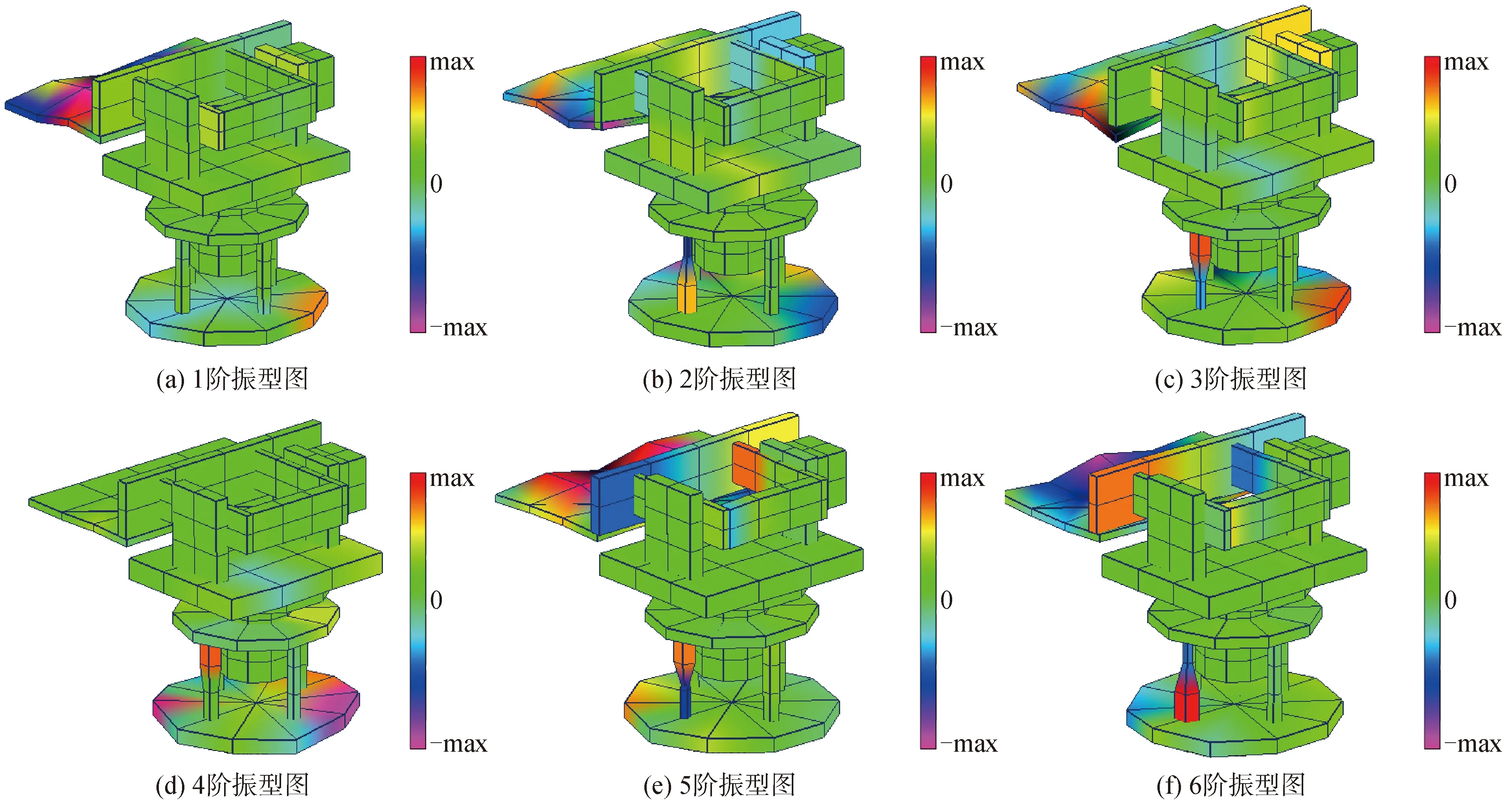
图8 激光追踪测量系统机械结构前6阶模态振型Fig.8 The 6 modes of the mechanical structure of the laser tracer measurement system
图8(a)为结构的1阶振型,结构变形较为不明显主要是光学底板的变形和底部支撑柱的变形;图8(b)~(d)为结构的2阶、3阶、4阶振型,主要是结构发生扭转时的受力振型,光学底板、仪器底板和4根支撑柱都有变形;图8(e)~(f)为结构的5、6阶振型,主要是仪器底座和光学底板的扭转变形,除了较为明显的光学底板变形外,俯仰轴支撑梁的前板也有发生变形。激光追踪测量系统机械结构的前6阶固有频率值随阶数的增加而增大,振动明显的部分主要集中在光学底板和底部支撑立柱的变形和扭转上,同时仪器底座也会有扭转变形,整体结果与仿真计算结果相一致。
仿真模态分析与试验模态分析的前6阶固有频率对比如表1所示,考虑到仿真的三维简化模型中去除了结构中全部的螺钉以及微小部件,与实际进行试验模态实验的结构有所差异,仿真与试验固有频率存在一定偏差。最终试验模态分析结果与计算仿真结果基本一致,螺钉等固定方式对结构固有频率产生影响。
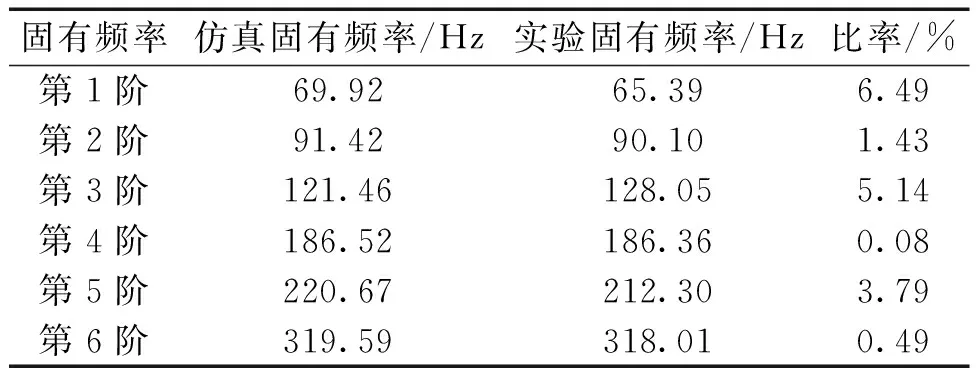
表1 仿真和实验的前6阶固有频率对比Table 1 The first six orders of nature frequency comparison
同时还进行了重复性实验,在相同测量条件下,重复上述实验过程5次,得到5组机械结构的实验模态结果,利用标准差σ分别为4.734、9.732、3.093、6.824、5.715、1.140进行重复性评定,如表2所示。
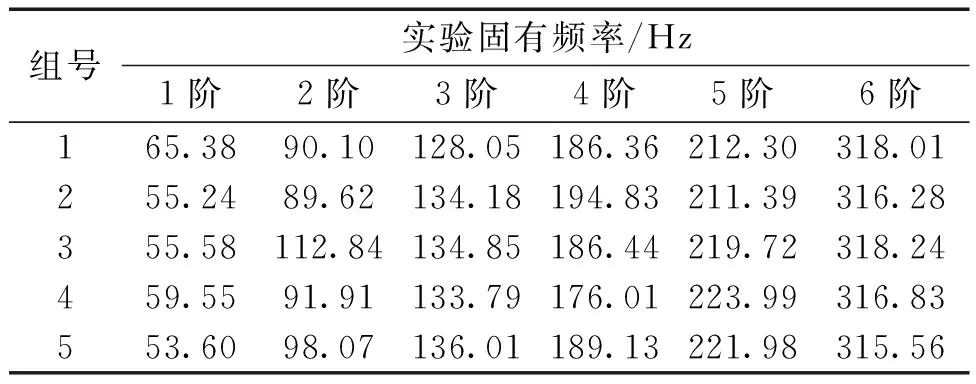
表2 机械结构的实验模态重复性实验结果Table 2 Repetitive experimental results
5 结论
1)机械结构存在的固有频率范围,在外界频率相近的激励下容易引起结构变形。
2)增加了系统的稳定性,提高机械系统的精度的优化方式,即机械系统的固有频率应远离控制系统的伺服带宽,通过改变回转电机支撑方式,考虑增大俯仰轴结构尺寸把光学元件放在结构内部,及光学元件考虑采用粘贴的固定方式。
3)为激光追踪测量机械结构系统的振动特性分析、振动故障诊断和预报,以及结构动力特性的优化设计提供了依据。
