砂土中吸力式筒形基础冲刷数值模拟分析
2023-05-04赵学亮隋淑环陈馨睿任彦忠吴成恩宋启明
赵学亮, 隋淑环, 陈馨睿, 任彦忠, 吴成恩, 宋启明
(1.东南大学 混凝土及预应力混凝土结构教育部重点实验室(东南大学), 江苏 南京 211189; 2.华北电力大学 河北省低碳高效发电技术重点实验室, 河北 保定 071003; 3.中广核(福建)风力发电有限公司, 福建 福州 350001; 4.福建永福电力设计股份有限公司, 福建 福州 350001)
吸力式筒形基础是近年来从深海基础中逐渐发展起来的一种新型海上风机基础,具有筒体入泥浅、海上施工周期短、施工成本低等优点,施工过程不需要复杂的嵌岩施工技术,安装过程无噪音,对环境友好。但筒形基础因阻水宽度大,在位工作期间受波浪和海流作用,基础周围土体极易受到冲刷,对海上风电机组的正常运行产生非常不利的影响。
在单向水流作用下,最大冲刷深度的影响因素主要有希尔兹数θ[1-2],相对水深hw/D(hw为水深,D为结构物直径)[3],泥沙级配[4],结构物尺寸[5-7],海床坡度[8]等。但对于结构物冲刷的研究集中于单桩基础,筒形基础作为一种新型海上风电基础,对其冲刷的研究较少。对于筒型基础局部冲刷问题的研究中,赵雁飞[9]建立了通过建立数值模型模拟了单桩基础和筒型基础周围的冲刷情况。于通顺[10]对3种不同比尺的复合筒型基础模型在粉砂质海床产生的局部冲刷情况进行模型试验,得到包括冲刷平衡时间、模型周围冲刷坑的范围、最大冲刷深度等的冲刷规律,并依据系列比尺模型试验原理推算得出实际工程中筒基的冲刷深度。Stroescu[11]对比单桩和单筒基础的冲刷形态,发现筒型基础自带防冲刷性质,在各种环境条件下,其表现类似于冲刷防护单桩。刘茜茜[12]通过物理模型试验研究变截面圆柱尺寸对基础局部冲刷的影响,结果发现筒型基础的最大冲刷深度与宽度随上部结构直径增大而增加,且当上部结构与主筒直径比值在0.2~0.5时,结构的防冲刷能力较好。
吸力式多筒基础在较深海域能表现出更好的安全和经济性,其筒与筒之间会因布置形式的不同导致基础周围水流特性的改变,从而影响局部冲刷。Sumer等[13]对波流共同作用下不同布置形式的群桩进行冲刷试验,分析了相对桩间距G/D(G为桩间距,D为桩径)和KC数对群桩基础局部冲刷的影响。Qi等[14]针对双柱基础研究其桩间距和水流攻角α对于冲刷深度的影响,并得出与G/D和α相关的双桩基础冲刷深度公式。刘明维等[15]对内河框架码头大直径桩柱串列及并列四桩柱绕流进行数值模拟,研究了桩柱周围的绕流流场形态和水动力特性,分析了流速、桩间距对遮流效应的影响。
由于海洋环境下吸力筒基础周围流场相对复杂,且筒形基础直径较大,模型试验因缩尺效应不能准确反映结构物周围冲刷形态,因此数值模拟成为研究吸力筒冲刷问题最有效和相对准确的方式。目前研究中,对于吸力筒基础冲刷问题的研究尚不充分,且多为单筒吸力筒基础,对于新型三筒基础的冲刷问题有待研究。本文通过CFD软件建立三维数值水槽,模拟砂土中单向流条件下海上风电吸力式筒型基础周围的局部冲刷,改变入射水流要素和筒基尺寸,通过分析吸力筒周围冲刷坑深度和地形,研究吸力式筒型基础的局部冲刷机理和影响因素。
1 局部冲刷数值分析
计算流体动力学(computational fluid dynamics,CFD)借助计算机对包含流体流动、热传导等相关物理现象的系统进行数值计算,并通过图像显示进行分析,利用流动基本方程对流动过程进行数值模拟。
1.1 湍流模型
常用的湍流模型包括普朗特混合长度模型、一方程模型、标准k-c模型、重正化群(renormalized group, RNG)k-ε模型以及大涡(large eddy simulation, LES)模型。其中RNGk-ε模型通过对湍动粘度的修正,考虑到了平均流动中的湍流涡旋及旋流流动情况,从而提高了模拟精度,因此本研究选用RNGk-ε模型。
1.2 自由表面处理方法
基于界面重构技术的自由表面处理方法(volume of fluid method,VOF)基于流体体积的百分比,每个网格(控制体积)在本身具备的流体属性外又增加了一个流体体积百分比函数F。计算自由表面随时间的变化,需要移动网格中的体积百分比,流体百分比的变化应满足的输运方程为:
(1)
式中:u、v、w分别为x、y、z方向上的速度分量。求解输运方程得到的每个单元体的F值可用以确定自由表面所在的单元。
1.3 泥沙冲刷模型
本文依托实际工程海域条件和工程地质环境,冲刷模型针对无粘性沙,通过预测泥沙的侵蚀、对流及沉积来估计泥沙的运动。
基于床面剪切应力τ的希尔兹数θ为:
(2)
式中:g为重力加速度;ds为沉积物中值粒径;ρx为沉积物密度;ρf为水密度。
床面泥沙启动可借助临界希尔兹数θcr来确定。临界希尔兹数θcr基于广泛使用的Soulsby[16]提出的经验公式进行计算:
(3)
考虑到沉积物坡度对泥沙起动的影响,式(3)可以改写为:
(4)
式中:D*=[g(ρx/ρf-1)/v2]1/3ds;v是流体粘滞系数;β是河床坡度;ψ是水流方向和坡度方向之夹角;φ为泥沙静止角。
悬移质沙通过与流体间的对流产生输运。如果不考虑VOF和FAVOR网格处理技术 (fractional-area/volume obstacle representation,FAVOR),悬移沙的输运方程为:
(5)
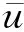
(6)
(7)
由方程(6)、(7)可以求出漂移速度。
采用梅叶-彼德(Meyer-Peter Muller)公式对推移质输运进行计算。平面单宽体积输沙率由该模型预测可得:
(8)
式中:βs为推移质系数,用于预测床面剪应力超过临界剪应力时推移质沙输运的几率,其默认值为8.0。
2 吸力筒基础冲刷数值模型
本研究模拟砂土中恒定流条件下海上风电吸力式筒型基础周围的局部冲刷。图1为参考实际工程吸力筒尺寸建立的基础模型图,吸力筒单筒基础和多筒基础的各筒直径D均为10 m,筒长L为10 m,单筒基础上下结构直径比为0.4,多筒基础的相对筒间距G/D为2.5(G为三筒基础各筒中心点之间的距离)。
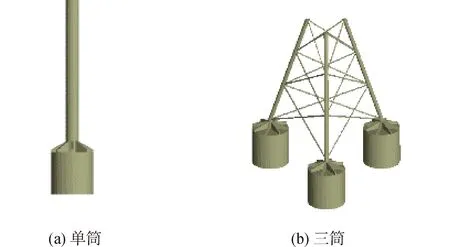
图1 吸力筒基础模型Fig.1 Suction bucket foundation models
2.1 模型建立
模型尺寸考虑入射波流稳定以及消除边界效应的影响,选取X方向总长为220 m(22D),Y方向宽度为80 m(8D),Z方向高度为38 m。设置结构物在模型中心,考虑我国近海岸实际情况,控制水深为25 m。为了减小初始模拟时来流水流对入口和出口边界处河床的淘刷,在上游入水口处、下游出水口设置厚2 m、宽70 m、高8 m的稳水挡板,模型底部铺设置8 m厚的床沙(图2)。网格划分X方向220个,Y方向80个,Z方向90个网格,为提高计算精度,采用嵌套网格法在筒周一倍筒径处和床附近进行局部网格加密[17]。

图2 数值模型与边界条件布置Fig.2 Sketch of numerical model and boundary conditions
在边界条件的设置中,单向流工况的入口选择速度作为边界,给定水流边界为均匀入流V,水流流速Uc为1.5 m/s,边界的入流水深设置为25 m。设置出口边界条件为静水压力边界P,流体高度以控制出流水深不变为条件,设置为水面高度。计算区域左右两侧为对称边界,上边界采用刚盖假定,各物理量的垂向梯度为0。底部边界条件设置为壁面无滑移条件。
初始水体设定在挡板上下游之间,上游初始水位与下游保持一致,水面无坡降,采用静水压力。设置Z方向为重力方向,重力加速度为-9.81 m/s2。冲刷模块中,泥沙中值粒径ds为0.135 mm,密度为2 670 kg/m3,水下休止角为30°。模拟为单一不可压缩流体,双精度条件。
2.2 数值模型验证
为验证数值模拟结果的合理性,选取Zhao等[5]的物理模型试验进行对比验证。以模型试验中test C工况为验证工况,结构物尺寸(长×宽×高)为40 cm×20 cm×20 cm,中值粒径ds=0.135 mm,泥沙比重ρx/ρf=2.67,临界希尔兹参数θcr=0.062 5,水深h=0.5 m,平均流速U=0.325 m/s。
首先对模型流场进行验证,沿水深方向设置测点,得到的水槽断面流速沿水深分布曲线,各流速测点的采样数据可按照流速对数分布规律进行拟合,即:
(9)
式中:uf为摩阻流速;z为流速测点距离理论底床零点的距离;ks为Nikuradse等效粗糙度。
图3对桩前行进水流断面流速进行对比,模型试验和数值模拟的断面流速重合度较高,且都满足对数分布规律,故模型流场拟合较好。

图3 水流速度沿水深分布对比Fig.3 Current velocity contribution with water depth
本文分别从冲刷形态、最大冲刷深度2个方面对试验和模拟的局部冲刷进行验证。从图4的地形云图对比可以看出,不同阶段下模型试验和数值模拟的冲刷地形结果基本一致,前期冲刷先发生在迎流侧桩角处,桩后两侧有八字形淤积。水流方向为自左向右t为10 min时,模型试验的最大冲刷深度S为5.8 cm,数值模型最大冲刷深度S为5.5 cm,两者相差5.5%,结果吻合较好。后期桩前侧冲刷坑逐步加深扩大,但最大冲刷深度仍发生在桩角处,桩后两侧淤积也逐步后移至正后方,桩周地形变化趋势与物理模型试验更为接近。t为1 h时,冲刷进入稳定阶段,模型试验的最大冲刷深度S为10.8 cm,数值模型最大冲刷深度S为10.1 cm,两者相差6.5%,结果基本吻合。由此,数值模型计算结果能够良好的反映物理模型试验的规律。
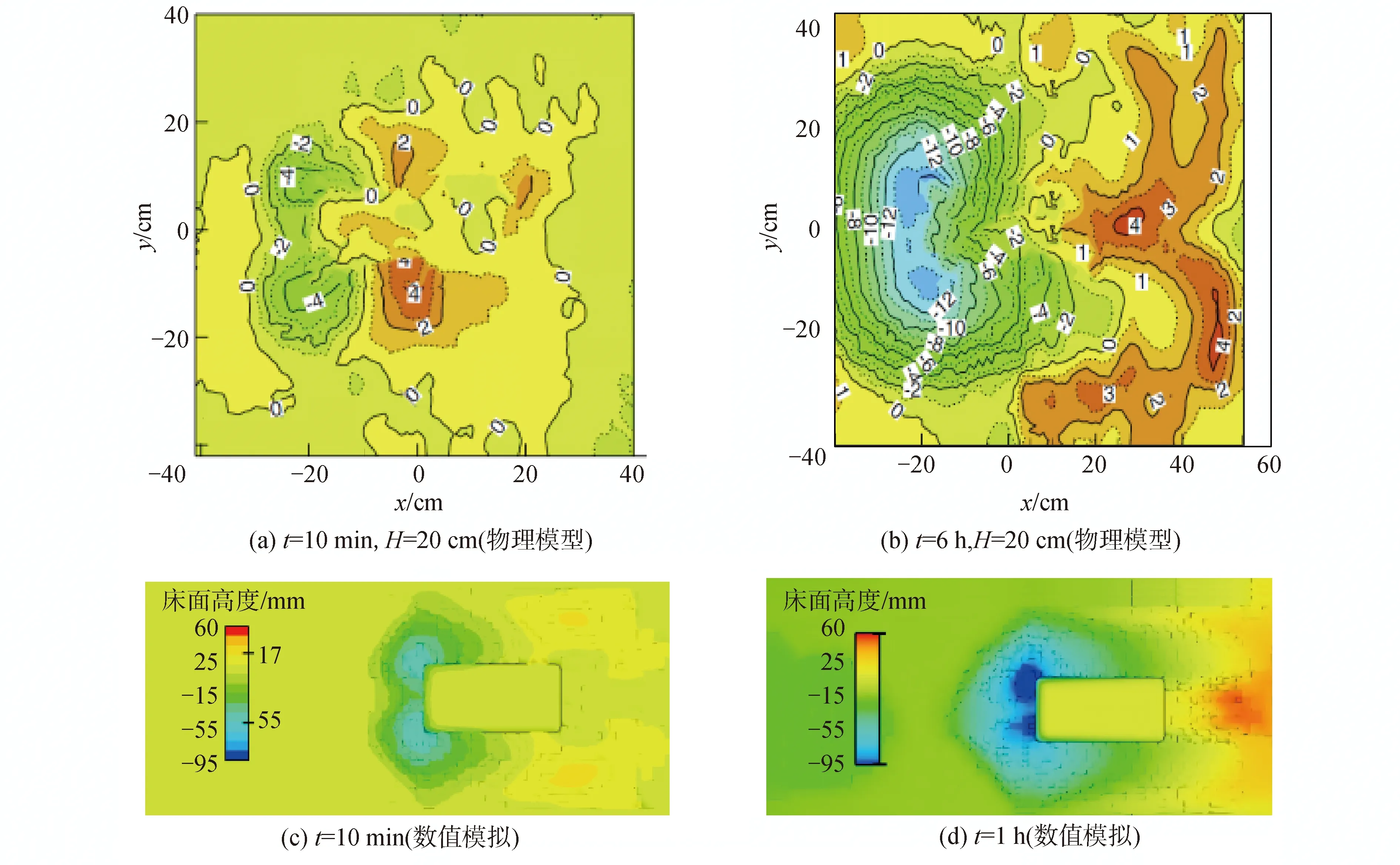
图4 物理模型试验与数值模拟地形云图对比Fig.4 Comparison of model test and numerical result of scour depth contour map
3 吸力筒局部冲刷机理与影响因素分析
3.1 吸力筒局部冲刷机理分析
根据实测潮流资料,选取水深为25 m、水流流速为1.5 m/s的单向流作为代表性水流条件。实际工程中吸力筒安装时,由于土塞的发生,筒体不能完全下沉至床面处。因此,设置吸力筒露出床面高度为0.1D,计算得到不同时刻的地形图见图5。
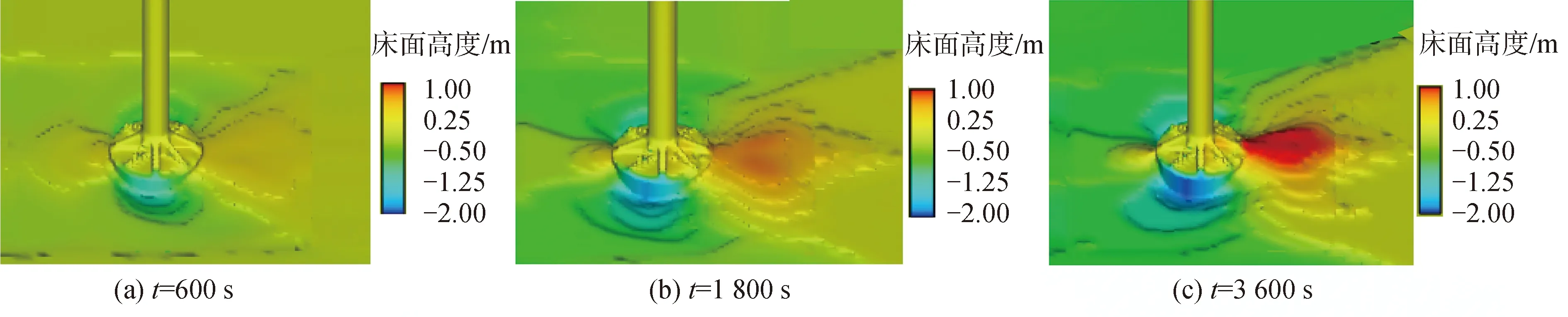
图5 单筒基础冲刷地形变化Fig.5 Process of scour around suction bucket foundation
通过对筒周冲刷坑形态变化的观察可以发现,侵蚀主要发生在吸力筒迎流侧两侧,最大冲刷位置发生在吸力筒迎流侧沿水流方向45°~90°。冲刷开始阶段,吸力筒两侧床面冲刷迅速发展,在10 min内最大冲深为1.246 m,已达到最大冲深的68.9%。随着床面高度的下降,冲刷深度随时间推移发展速度逐渐缓慢,且冲刷坑形态逐渐明显呈马蹄状,边坡与最大冲刷深度位置成一定角度保持不变,冲刷坑范围向外扩展。1 800 s开始,筒前后侧淤积逐渐明显,前侧泥沙淤积高度约0.081 m,远小于筒后侧淤积高度0.550 m。随着筒后淤积不断后移,冲刷坑的形态基本趋于稳定,3 600 s时冲刷深度达到1.809 m,约为0.18倍筒径,发生在筒周与水流方向夹角约为67.5°处,冲刷半径达到0.97D,此时局部冲刷趋于平衡。
露出床面部分同为0.1D的吸力式三筒基础在相同水流条件下,冲刷地形变化如图6,水流方向自左向右,即x轴正方向。可以看出,吸力式三筒基础的各筒冲刷坑形态和单筒相似,都为两侧冲刷,后侧淤积。

图6 三筒基础冲刷地形变化Fig.6 Process of scour hole around tripod-bucket foundation
各筒周围冲刷的发展趋势相似,都经历快速冲刷-缓慢冲刷-冲刷平衡的阶段,但平衡时达到的最大深度存在差异。3 600 s内,三筒基础的最大冲深发生在后筒内侧,深度达到2.441 m,比前筒最大冲刷深度1.809 m增加34.8%;后筒外侧冲刷呈波动上升趋势,最终冲刷平衡深度和前筒大致相同。通过对比可明显发现三筒基础的后侧桩基周围冲刷并非对称,内侧比外侧冲刷严重1.35倍。
图7~9分别为t=1 800 s时刻XY、XZ、YZ筒周平面流速分布图,从不同视角反映了冲刷过程中吸力筒基础周围的流场变化。可以看出,水流遇到吸力筒基础后发生绕流,桩前上部流速减小,经过基础两侧时流速增加,竖直方向上有向下的水流,靠近海床的底部有向上的水流,由于水流剪切层分离和桩前逆压梯度的影响,在桩侧形成马蹄形涡旋,导致床面切应力增大,从而在筒基两侧形成冲刷坑。水流经过桩基时,两侧边界层分离形成尾涡,尾涡在桩基下游脱落,桩后出现泥沙淤积。
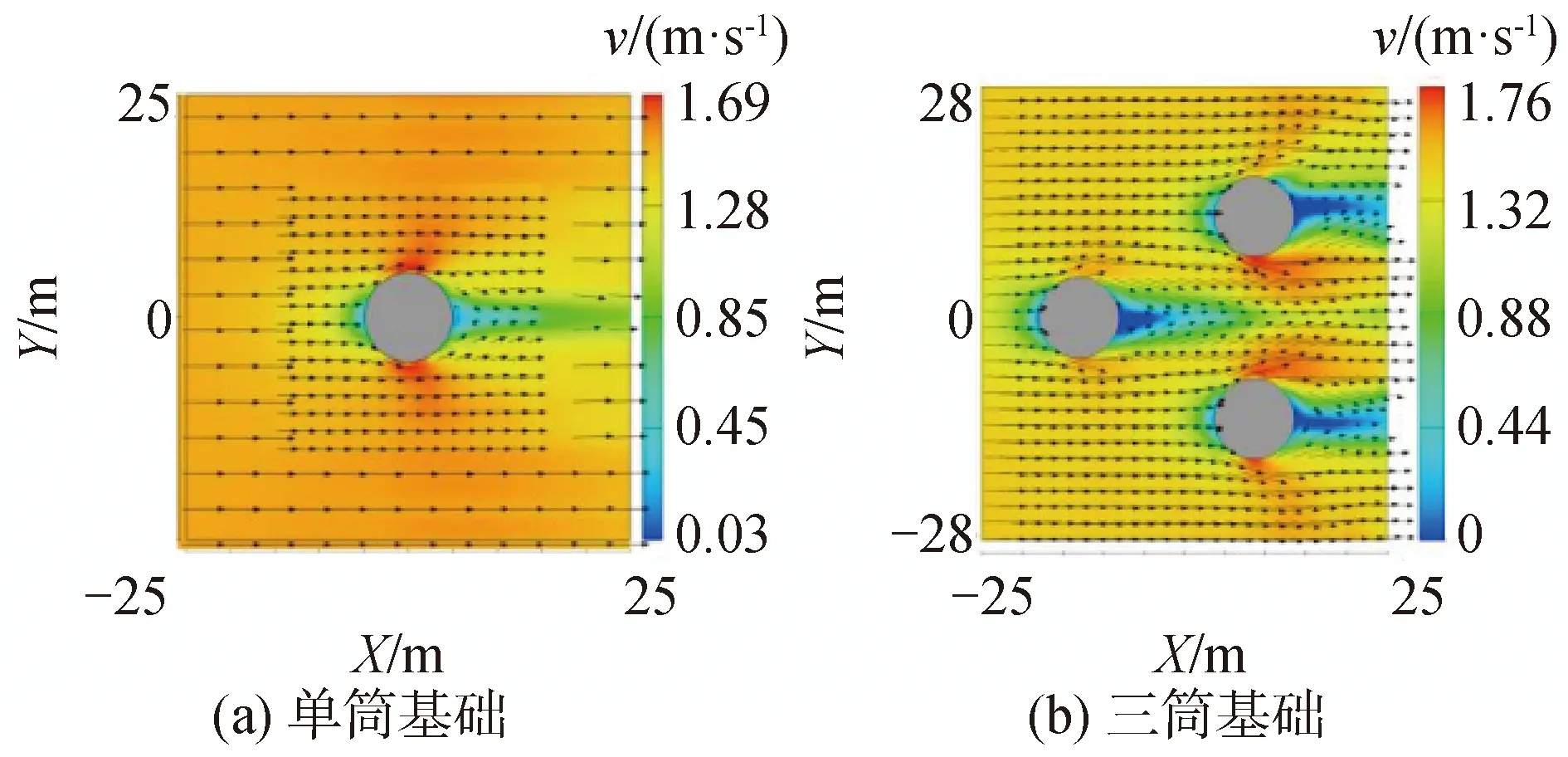
图7 XY平面流速分布Fig.7 Current contributions of XY plane

图8 XZ平面流速分布Fig.8 Current contributions of XZ plane
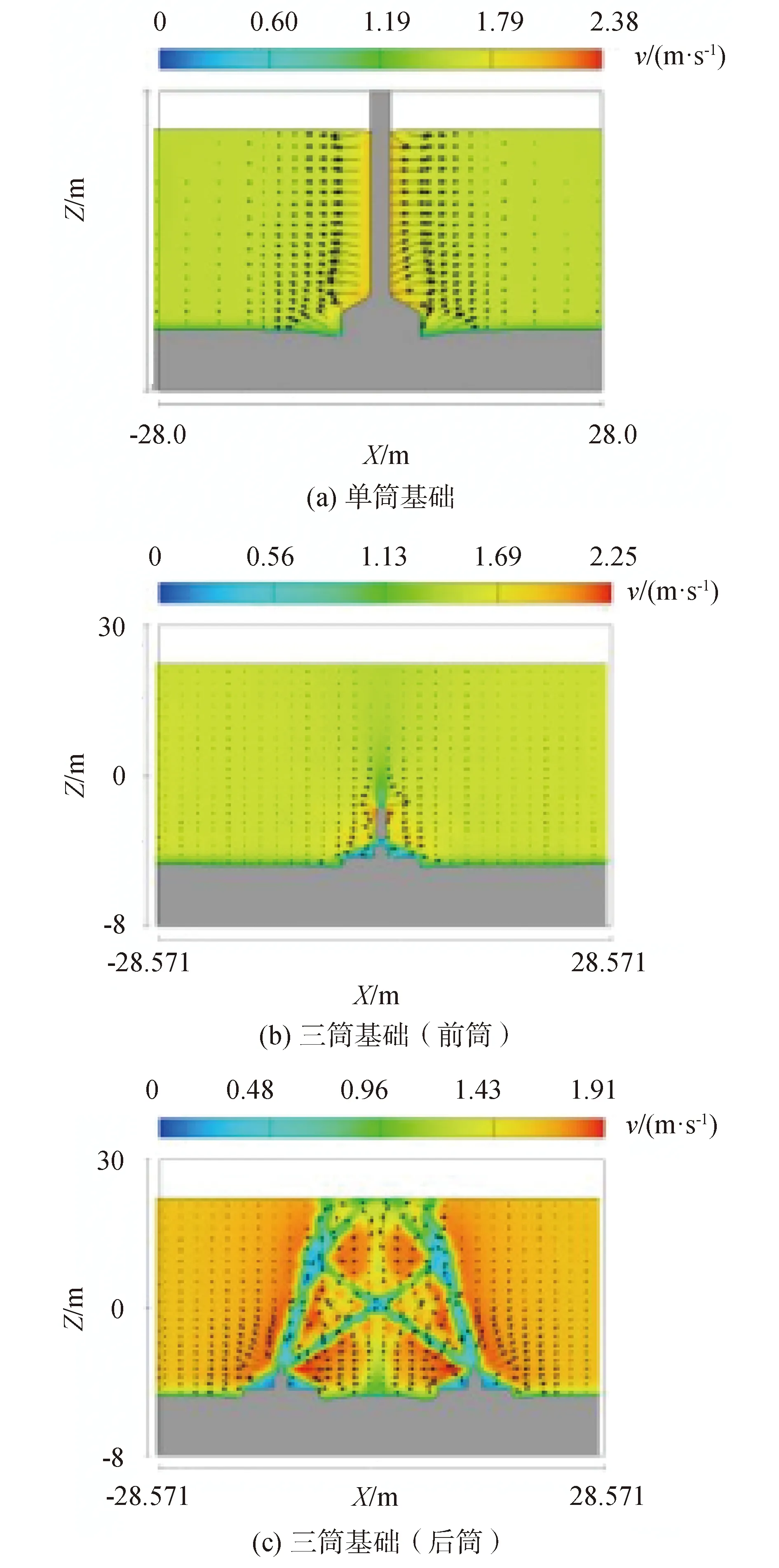
图9 YZ平面流速分布Fig.9 Current contributions of YZ plane
吸力式三筒基础受塔筒及支撑桁架的影响,床面上部流态紊乱,但靠近海床底部的各筒周流场变化与单筒基础类似。由于筒间存在互相影响,水流方向下游各筒基周围流场不对称,由XY平面流速分布图可以看出,上游水流经过前筒后发生绕流,由于后筒的阻碍,流线在后筒内侧集中并形成强度更大的桩侧马蹄涡,导致后筒内侧床面附近的水流流速局部增大,这也是形成冲刷坑不对称的主要原因。
3.2 吸力筒基础局部冲刷影响因素分析
3.2.1 高径比影响
露出海床部分基础尺寸对于结构物周围流场的形态有重要的影响。考虑实际工程中吸力筒下沉位置及筒顶结构高度,分别设置吸力筒露出床面高径比H/D为0、0.05、0.1、0.2(特别说明,这里的高径比是指吸力筒露海床面的高度H与筒径D的比值,与通常所说的整个吸力筒长度L与直径D比值的长径比L/D不同)。相同入射流条件下(水流流速Uc=1.5 m/s)不同高径比的吸力筒最大冲深随时间发展如图10所示。
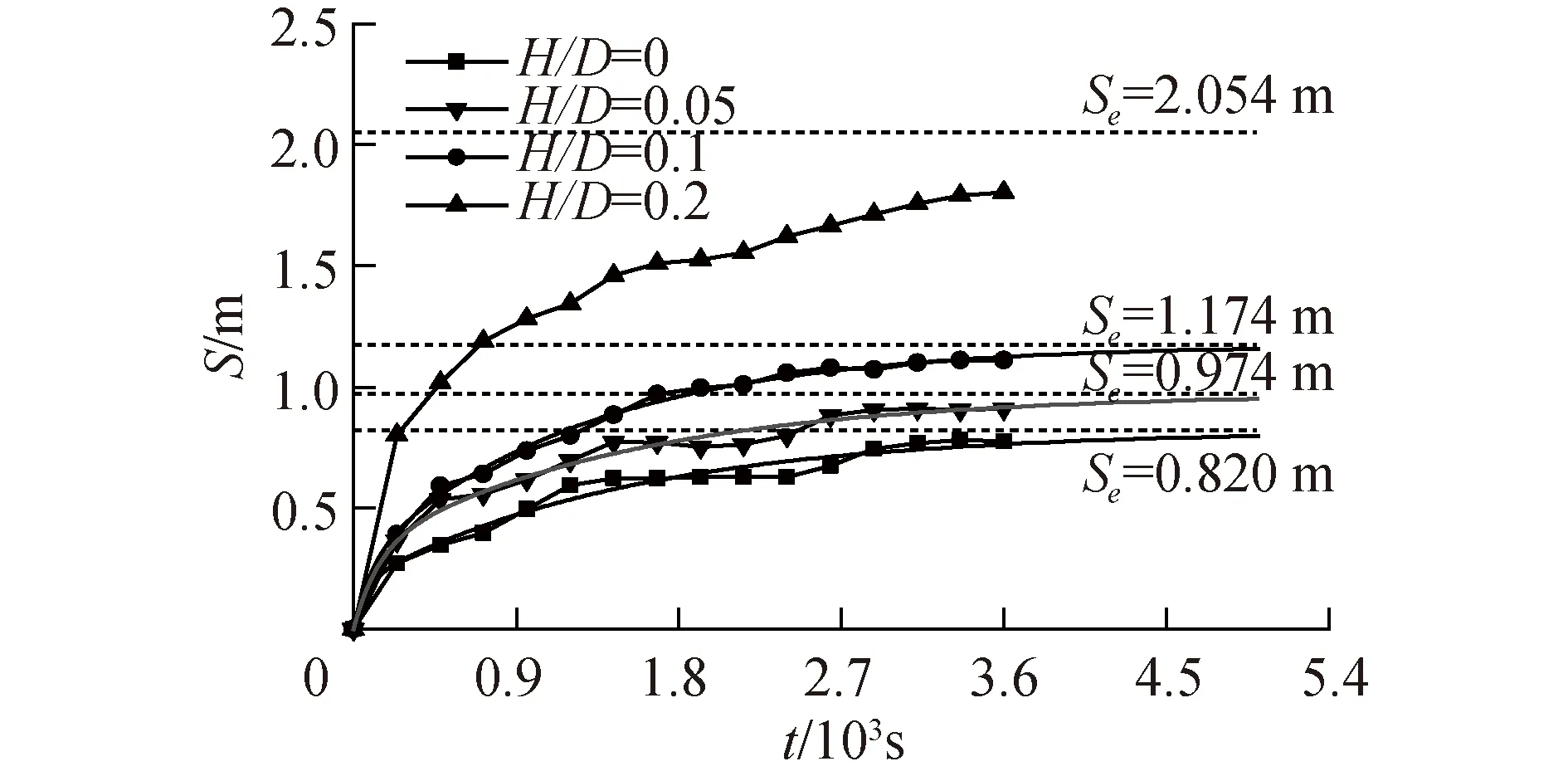
图10 不同高径比吸力筒的冲刷历程及拟合曲线Fig.10 Scour process around buckets with different high-diameter ratio and fitting curves
考虑到数值结果的稳定性和计算效率,各工况模拟冲刷时长统一取1 h,通过对比1 h内吸力筒的冲刷模拟情况,分析各参数对吸力筒基础的局部冲刷的影响规律。因1 h时冲刷还未达到完全平衡,最终的平衡冲深采用Sheppard[18]提出的单桩基础的冲刷深度与时间发展的指数函数关系来推算。
S(t)=a[1-exp(-bt)]+c[1-exp(-dt)]
(10)
式中:S(t)为时间t对应的冲刷深度函数;a、b、c、d为系数,可通过模拟所得数据采用最小二乘法进行拟合确定。当t取无穷大时,即可推算得平衡冲深Se=a+c。
图10为高径比分别为0、0.05、0.1、0.2的吸力筒基础的冲刷历程线,可以看出,不同工况下冲刷发展历史过程相似,分为3个阶段:快速冲刷、缓慢冲刷、冲刷平衡。冲坑形成初期,冲刷深度增加速率较快,600 s后增速逐渐放缓,最终冲刷深度趋于平稳,冲刷达到平衡。各工况的冲刷历时线与式(9)拟合的R2均大于0.9。R2为拟合优度,代表公式与原始数据的拟合程度,数值越接近1拟合程度越好。由此可知,式(9)也同样适用于吸力筒基础的冲刷历程拟合。由拟合函数可以推算出高径比H/D为0、0.05、0.1、0.2的吸力筒平衡冲刷深度分别为0.820、0.974、1.174、2.054 m。由图11的高径比和冲刷平衡深度的关系曲线,可以看出平衡冲深随高径比增大而增大,且增速也随高径比提高。分析原因是,吸力筒露出床面的部分越多,阻水面积越大,水流在筒周产生的马蹄涡强度越大,冲刷程度越大。
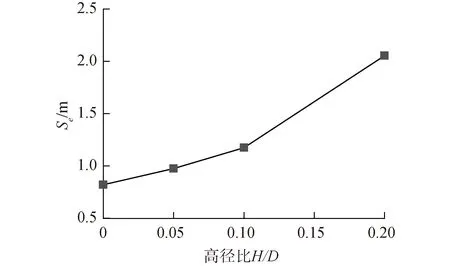
图11 高径比和平衡冲深的关系曲线Fig.11 Curve of high-diameter ratio vs. equilibrium scour depth
3.2.2 水流因素影响
吸力筒基础工作区域水流运动复杂,故本模拟设定了不同流速的恒定流条件,研究流速对吸力筒周局部冲刷的影响。由3.2.1节结论可得高径比为0.2时,平衡冲深能达到0.21D,冲刷坑的形态也更明显,为了更清晰地研究水流因素对于冲刷的影响,后续模拟仍选择高径比为0.2的吸力筒模型。
由图12可以看出,流速对于最大冲深有较大影响。当Um<1.5 m/s时,冲刷趋势遵循快速冲刷-缓慢冲刷-冲刷平衡的3个阶段。Uc=0.5、1、1.5 m/s时,平衡冲刷深度Se分别为0.108、0.894、2.054 m。当Uc=2 m/s时,冲刷首先进入快速发展的阶段,但当450 s后,冲刷深度开始波动上升,且冲刷速率减缓,拟合得冲刷平衡深度Se为4.970 m。当Uc=2.5 m/s时,冲刷深度波动上升的幅度更大,平衡冲刷深度可达7.979 m。以上分析可得,当单向流流速大于2 m/s时,冲刷发展过程变为快速冲刷-波动冲刷-冲刷平衡的3个阶段,图13为水流流速和平衡冲刷深度的关系曲线,可直观看出,流速越大,其对于平衡冲深的影响越剧烈;通过图12各拟合曲线的对比可得,流速越大,吸力筒周达到冲刷平衡所需时间越长。
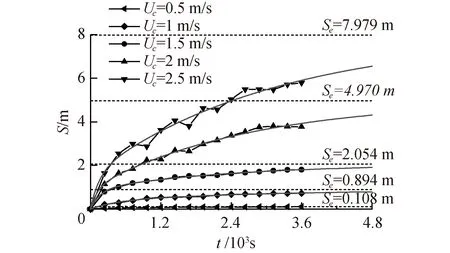
图12 不同流速下冲刷时间历程线Fig.12 Scour process around buckets under different current velocity and fitting curves
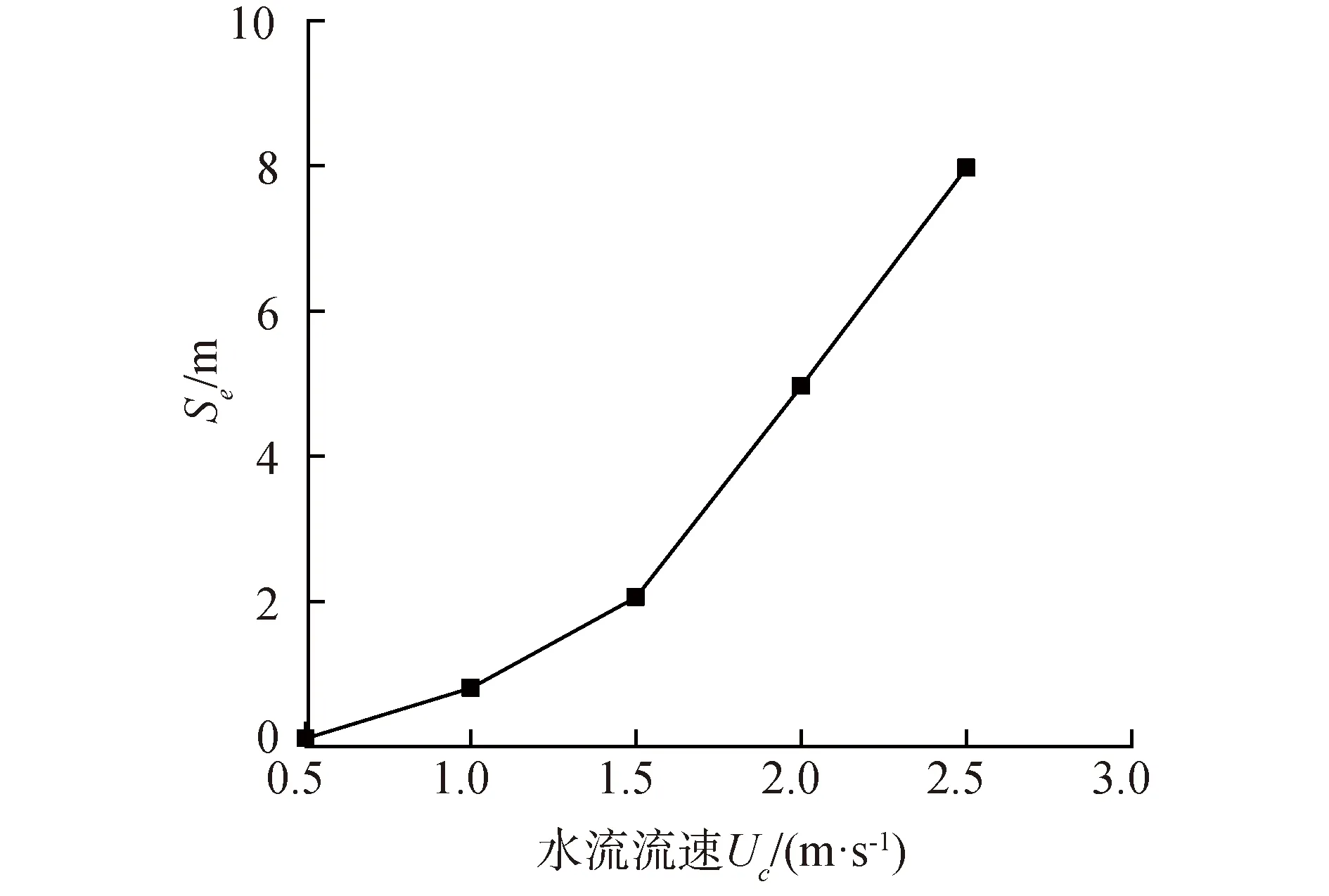
图13 流速与平衡冲深的关系曲线Fig.13 Curve of current velocity vs. equilibrium scour depth
3.2.3 筒间距影响
吸力式三筒基础的筒间距G是影响局部冲刷的重要影响因素。筒间距小于1.5D(D为单筒直径)时,与单筒基础区别不明显,不具备组合式多筒基础分析意义;当筒间距大于4D时,整体结构不利于实际施工,没有现实研究意义。有研究认为多筒基础的筒间距对吸力筒结构整体用钢量和水平极限承载力有较大影响,在满足承载力的基础优化上推荐长径比为1.25的三筒基础相对筒间距G/D值为3[19],故本研究建立4种吸力式三筒基础,筒间距G分别为2D、2.5D、3D、3.5D。
图14对比了不同筒间距的三筒基础在单向流(Uc=1.5 m/s)下,各筒的冲刷深度随时间变化曲线。可以看出各曲线发展趋势相似,重合度较高,即筒间距对于水流方向上游筒基的局部冲刷影响不明显,且与单筒基础的冲刷历程比较相似。图14(b)中筒间距G≤3D时各曲线重合度较高,冲刷历程相似,且1 h时的冲刷深度明显高于单筒基础,筒间距G=2D,2.5D,3D时,后筒内侧冲刷深度对比单筒基础分别增加38.7%、34.8%、31.5%,但当筒间距G>3.5D时,后筒内侧冲刷深度只增加了9.9%。说明当筒间距G≤3D时,其对于后筒内侧的局部冲刷影响较大,冲刷深度随筒间距的提高而减小;当筒间距G>3.5D时,其对于后筒内侧冲刷坑深度的影响迅速下降。原因为水流流经后侧两筒时,筒间压缩水流导致筒内侧局部水流流速增强,而该增强效应随着筒间距的增大而逐渐减弱。由图14(c)中可以看出不同筒间距的筒基外侧冲刷发展相似,都经历快速冲刷-波动发展-缓慢冲刷阶段,且冲刷1 h时冲刷坑最大深度与单筒基础相差较小,可见筒间距对后筒外侧几乎没有影响。综上分析,吸力式三筒基础筒间距G≤3D时,水流方向下游的筒基内侧的局部冲刷受筒间距G影响较大,冲刷坑随G变大而缓慢变深,但当筒间距G>3.5D时影响变小。
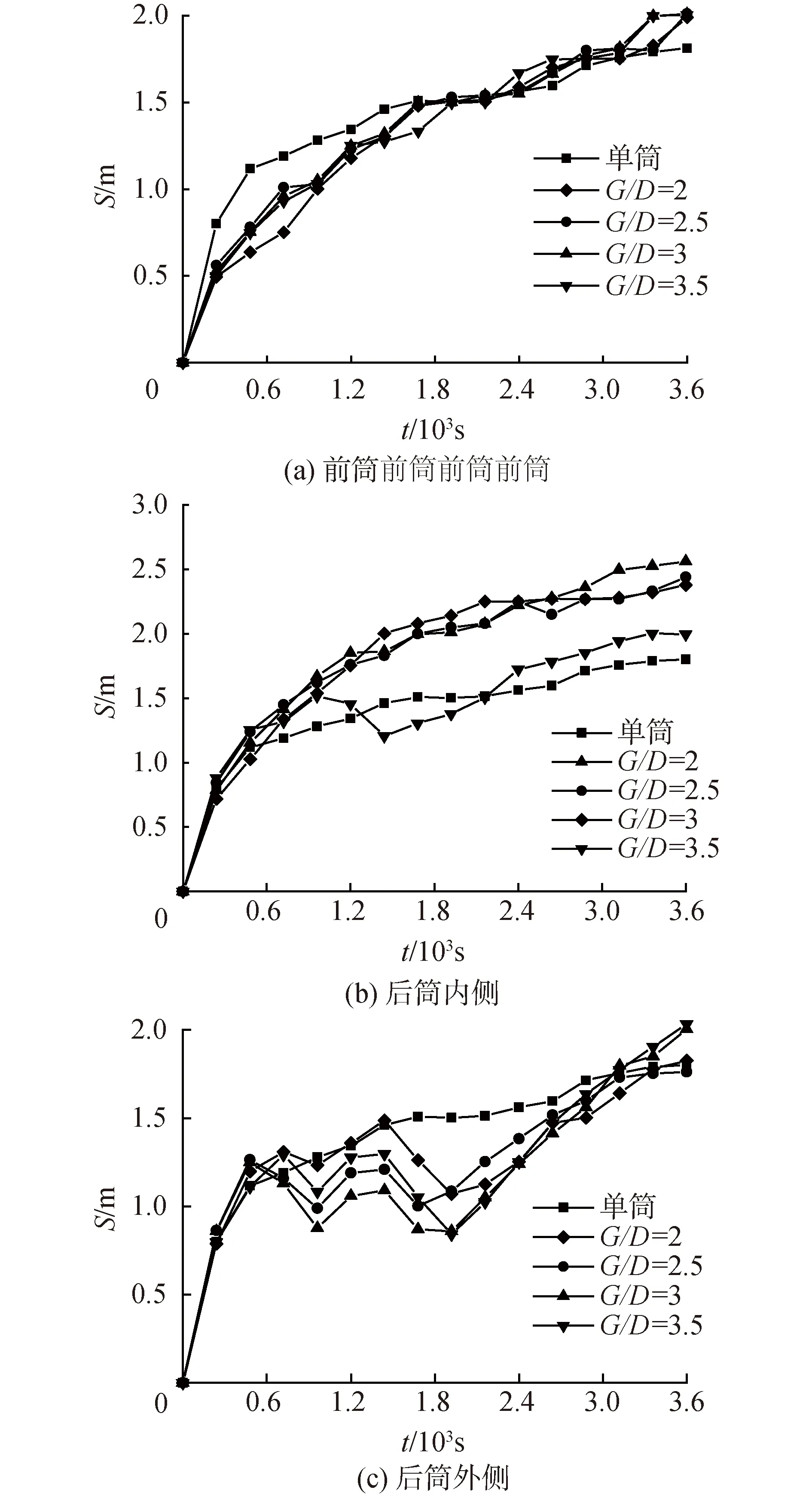
图14 不同筒间距的三筒基础各筒冲刷历程Fig.14 Scour process around each bucket with different bucket spacing
4 结论
1)吸力式单筒基础的冲刷较相等直径的单桩基础程度较小,冲刷坑呈对称马蹄状,3 600 s时冲刷深度S达到1.809 m,约为0.18D,发生在筒周与来流方向夹角约为67.5°处,冲刷半径达到0.97D。三筒基础各筒周冲刷形态接近马蹄状,但形状不对称,后侧桩内侧冲深比外侧深1.35倍。
2)不同高径比的筒形基础局部冲刷发展历史过程相似,分为3个阶段:快速冲刷-缓慢发展-冲刷平衡。但最大冲刷深度和平衡时间有所差异,吸力筒露出床面的部分越多,冲刷程度越大,达到冲刷平衡更慢。
3)单向流流速较低时,冲刷趋势遵循快速冲刷-缓慢冲刷-冲刷平衡的3个阶段,而当单向流流速较高大于2 m/s时,冲刷发展过程变为快速冲刷-波动冲刷-冲刷平衡的3个阶段,且流速越大,其对于最大冲深的影响越剧烈。
4)吸力式三筒基础的筒间距G对水流方向下游的筒基的局部冲刷影响较大,会扩大筒基内侧冲刷坑的深度和宽度,且该影响随着G的扩大不断变弱,当G>3.5D时,其影响可忽略不计。
