归纳思维的理论探析及其在小学数学中的应用*

□陈 蒨 徐文彬

归纳思维是数学思维的基本方法之一，在数学研究和数学学习中有着丰富且独特的应用。高斯曾经说过，运用归纳思维可以萌发出极漂亮的新的真理［1］。《义务教育数学课程标准（2022年版）》在核心素养主要表现部分强调了要“能够通过简单的归纳或类比，猜想或发现一些初步的结论”。由此可见，在数学教学中，归纳思维至关重要。本文将从理论的角度对归纳思维进行深度剖析，并基于教学实践探析归纳思维在小学数学中的应用。

一、问题的提出

引例：仔细观察下面的式子，你有什么发现？

6=3+3

8=3+5

10=3+7=5+5

12=5+7

14=3+11=7+7

16=3+13=5+11

……

分析：观察这些等式，这些等式左边都是偶数，右边都是两个奇质数的和，这就是著名的“哥德巴赫猜想”。1742年，德国数学家哥德巴赫就是运用归纳思维提出了这个著名的猜想：任何一个大于4的偶数都是两个奇质数之和。

通过“哥德巴赫猜想”这一引例，我们可以看到归纳思维的重要性。其实，数学史上很多假说和猜想都是运用归纳思维提出的，比如著名的“四色猜想”“费马猜想”“梅森猜想”等。那么归纳思维的内涵究竟是什么？归纳思维有哪些类别？归纳思维在小学数学中又有哪些应用呢？下面将对归纳思维进行理论剖析，并通过数学教学实践对归纳思维在小学数学中的应用进行探析。

二、归纳思维的理论探析

归纳思维是数学发现和创造的基本方法，同时又是解决数学问题的重要思想方法。下面将从归纳思维的内涵和归纳思维的类别两方面展开对归纳思维的理论探析。

（一）归纳思维的内涵

归纳思维是通过对某类事物中的若干特殊情形的分析得出一般结论的思维方法。归纳思维的认识依据在于同类事物的各种特殊情形中蕴含的同一性和相似性。［2］116归纳思维具有以下特征：一是归纳思维必须把实践归入思维的过程，以各种感性的、具体的材料作为思维的前提，要从具体的、个别的事物中概括出一般；二是归纳思维推出的结论具有或然性，要使之成为可靠的结论需要严格的证明和实践的检验；三是归纳思维是个体从感性认识上升到理性认识的工具，个体在感性认识的基础上，通过归纳思维获得新概念、新判断或新理论。［3］

（二）归纳思维的类别

归纳思维有多种分类方法，根据考查对象的范围是涉及了某类事物的一部分还是全体，可把归纳思维分为两种类别：不完全归纳和完全归纳。

1.不完全归纳

不完全归纳是根据某类事物的部分对象具有（或不具有）某种属性而得出该事物的全体也具有（或不具有）这种属性的思维方法。［2］117其推理形式如图1。不完全归纳又称经验归纳，由于仅根据所考查的部分对象就得出一般性的结论，因此，常常带有想象、猜测等主观臆断的成分，所以得出的结论具有或然性。

图1 “不完全归纳”的推理形式

不完全归纳是激发创造性思维的基本方法，推动着数学的发现和发明。古往今来，很多数学家都是运用不完全归纳的思维方法来提出猜想的，比如引例中的“哥德巴赫猜想”。小学数学中也经常用到不完全归纳，常见的“找规律填数”就是根据有限项（部分对象）具有的某种共同的属性，从而运用不完全归纳得出规律，再把得出的规律用到未知项（未知对象）中。此外，不完全归纳在“探索规律（如间隔排列、钉子板上的多边形等）”“2、3、5 的倍数特征”“运算律”“字母表示数”“图形的性质与特征（三角形/多边形内角和、三角形三边关系等）”“可能性”等相关内容中有着广泛的应用。

2.完全归纳

完全归纳是根据某类事物的每个对象都具有（或不具有）某种属性而推出该类事物的全体具有（或不具有）这种属性的思维方法。［2］118完全归纳的推理形式如图2。由于这一思维方法考查了某类事物的所有对象或一切特殊情况，所以得出的结论必定是正确的，因而是一种严格推理。

图2 “完全归纳”的推理形式

完全归纳有助于概括和证明，能得到正确的结论。上面提到的“四色猜想”就是运用完全归纳证明的。［4］小学数学中用到的完全归纳比较少，主要与分类讨论相结合。比如，要得出“两个加数奇偶性相同，和一定是偶数”这一结论，便可以分为两类分别讨论，一类是“两个加数均为奇数，和一定是偶数”，另一类是“两个加数均为偶数，和一定为偶数”，如此便可运用完全归纳得出结论。

特别要指出的是，不完全归纳和完全归纳都属于归纳推理，只是推理的强度不同。而“数学归纳法”虽然名字里面有归纳，但它并不属于归纳推理，而属于演绎推理。原因有二：其一，完全归纳不能用于无穷集合；其二，数学归纳法是典型的三段论，其基础是自然数列的性质，也就是皮亚诺公理中提到的自然数的后继性［5］。

三、归纳思维在小学数学中的应用

数学家舒尔指出，在数学研究中，归纳思维起着重要的作用。［6］波利亚也提出，数学是学习归纳思维最合适的材料。［7］由此可见，归纳思维能推动数学的发展，数学的学习也能推动个体归纳思维的发展。小学数学中渗透着很多有关归纳思维的内容，下面将从数学教学实践的角度，讨论归纳思维在“数与代数”“图形与几何”和“统计与概率”领域的应用。

（一）“数与代数”领域的应用

小学数学中，“数与代数”领域中很多内容都渗透着归纳思维，较为典型的有“探索规律（如找规律填数、间隔排列、有趣的乘法计算等）”“运算律”“2、3、5的倍数特征”“用字母表示数”等相关内容。下面以“间隔排列”为例进行分析说明。

课例1：间隔排列

苏教版教材三年级上册《间隔排列》是一节探索规律的课。图3 呈现了小兔与蘑菇、木桩与篱笆、夹子与手帕的排列。观察每排两种物体的排列，它们有什么特点？比较每排两种物体的数量，你有什么发现？

图3 《间隔排列》主题图

【教学片段1】

师：请大家说一说你的发现。

生：小兔的只数比蘑菇的个数多1，木桩的根数比篱笆的块数多1，夹子的个数比手帕的块数多1。

师：还有补充吗？这三组数据有没有什么共同点？

生：每排第一种物体都比第二种物体多1。

师：是啊，反过来，每排第二种物体都比第一种物体少1。也可以说，每排两种物体的数量相差1。

师：每排两种物体的数量为什么会相差1 呢？

……

教学分析：教学片段1 呈现了“探索间隔排列规律”的学习过程。可以看到，间隔排列规律的初步得出需要学生对三组数据进行观察、分析，基于三组数据的共同属性，运用不完全归纳来思考。《间隔排列》这节课体现了归纳思维和演绎思维的结合。在教学片段中，仅根据三组数据运用不完全归纳得出的“每排两种物体的数量相差1”这一结论不一定是正确的，还需要通过演绎思维来验证或证明。于是教师及时追问“为什么两种物体的数量会相差1”，引导学生进一步思考，并让他们用圈一圈、连一连等操作把两个相邻的不同物体看成一组，结果最后有1 个多余，从而证明了这一结论的正确性。这节课的教学就是要引导学生通过归纳思维来发现规律，再通过演绎思维来证明规律，这是数学发现与发明的重要方法。

（二）“图形与几何”领域的应用

小学数学中，“图形与几何”领域也有很多内容的教与学都需要运用归纳思维，比较典型的有“图形与几何”中的“规律（如钉子板上的多边形、表面涂色的正方体等）”“图形的特征与性质（如三角形三边关系、三角形/多边形的内角和）”等相关内容。下面以“三角形的内角和”为例进行分析说明。

课例2：三角形的内角和

苏教版教材四年级下册“三角形的内角和”中，教材呈现了一个例题的主题图（如图4）。这个内容旨在引导学生探究三角形的内角和。

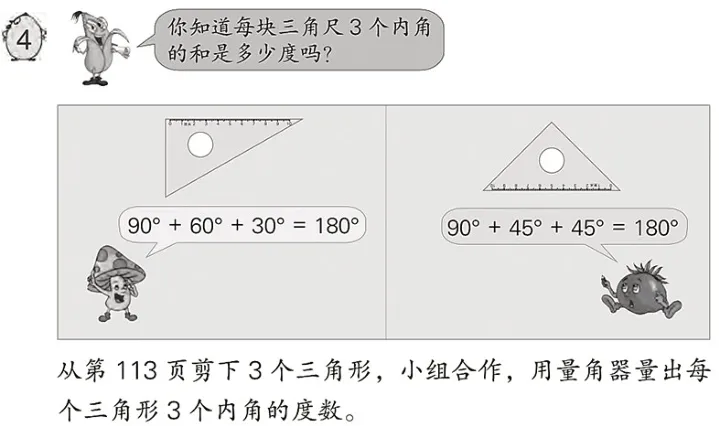
图4 “三角形的内角和”主题图

【教学片段2】

师：今天我们一起来研究三角形的内角和。我们可不可能研究完所有三角形的内角和是多少？你认为要研究三角形的内角和，只需要研究哪几种三角形的内角和就可以了？

生：直角三角形、锐角三角形、钝角三角形。

（教师引导学生通过量一量、算一算等活动，分别研究提供的直角三角形、锐角三角形、钝角三角形的内角和。）

（生提出猜想：三角形的内角和都是180°。）

师：怎样验证大家的猜想？

（小组合作，运用不同的方法验证并交流。学生提出度量验证、剪拼验证、折拼验证等方法。）

师：刚才大家验证了那么多不同的三角形，有没有穷尽所有不同的三角形？

生：没有。

（教师借助几何画板演示，任意变化三角形验证其内角和。最后，教师介绍帕斯卡的证明方法。）

教学分析：“三角形的内角和”这一内容充分体现了归纳思维的应用。第一，把三角形分成直角三角形、锐角三角形、钝角三角形来研究体现了完全归纳的思维。第二，在量一量、算一算等活动中提出猜想“三角形的内角和是180°”，这个过程充分运用了不完全归纳的思维。第三，全班通过度量、剪拼、折拼等方法验证不同的三角形，虽然验证了四五十个不同的三角形，但仍然是极其有限的，对猜想的验证仍然属于不完全归纳。第四，利用几何画板任意拖动三角形的顶点改变其形状、大小，不管如何变化，三角形的内角和始终为180°，这样验证的不同三角形的个数从有限趋向于无限，归纳思维的运用也从不完全归纳趋向于完全归纳，因此更加有说服力。第五，帕斯卡的证明是严谨的数学证明，属于演绎推理，能完全证明猜想的正确性。这一内容的教学，既渗透了归纳思维，又渗透了演绎思维，归纳思维用于发现结论，演绎思维用于证明结论的正确性。

（三）“统计与概率”领域的应用

逻辑学指出，概率通常是指应用于推理的归纳概率。［8］赖欣巴哈关于概率基础的描述指出，概率被定义为无限一般事件序列的性质，由于不知道无限事件序列的极限，所以只能根据这些序列的有限初始段进行归纳推理，从有限推断无限。［9］所以概率中体现着归纳思维。小学数学中，“统计与概率”领域中“随机现象发生的可能性”这部分内容中渗透着概率，同样也渗透着归纳思维。下面以《可能性》为例分析归纳思维的应用。

课例3：可能性

苏教版教材四年级上册《可能性》中，教材呈现了两道例题的主题图（如图5）。《可能性》这一课引导学生在摸球、摸牌等游戏中认识可能性，感受可能性有大有小。

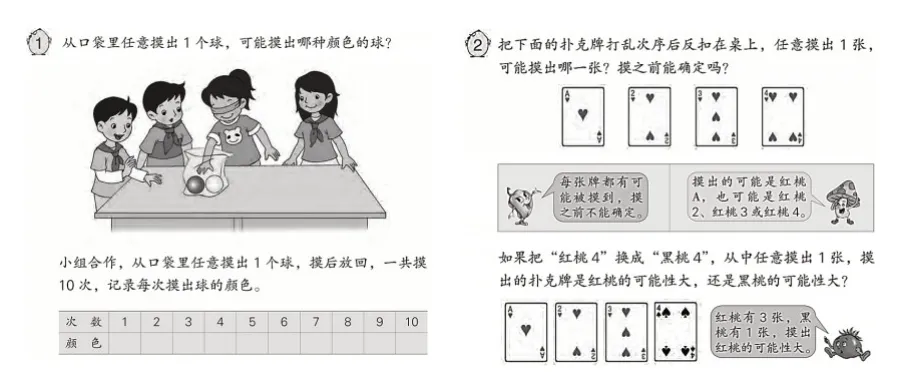
图5 《可能性》主题图

【教学片段3】

（教师组织全班学生分小组进行摸牌游戏，学生汇报后用表格呈现各小组数据。）

师：仔细观察每个小组的摸牌结果，结合你们组摸牌的情况，说说你的想法。

生：每个小组都是摸到红桃的次数多，说明摸到红桃的可能性大。

生：每个小组摸到红桃的次数都差不多是摸到黑桃次数的3倍，所以摸到红桃的可能性是摸到黑桃可能性的3倍。

师：为什么摸到红桃的可能性会比摸到黑桃的可能性大呢？

……

教学分析：《可能性》一课体现了归纳思维的应用。教学片段3中呈现的是摸牌游戏的教学过程。在全班学生参与摸牌游戏后，得到每个小组摸到红桃、黑桃的数据并以表格的形式呈现，引导学生观察数据再说想法，这一过程其实就是引导学生根据各小组的数据，通过归纳思维得出关于可能性大小的判断。要注意的是，这种根据归纳思维得出的结论只是学生对可能性大小的一种初步的感知，所以教师一定要追问“为什么摸到红桃的可能性比摸到黑桃的可能性大”，以此来引导学生进一步说理。这种归纳思维与演绎思维的结合能让学生对可能性有更加清晰的认识，也为后续概率的学习奠定了基础。

小学数学中归纳思维的应用是比较浅层次的，大多是不完全归纳。尽管如此，归纳思维仍然发挥着巨大的作用，学生通过观察、归纳去探索、发现甚至创造。数学课堂中归纳思维的应用还进一步促进了学生归纳思维的发展，同时结合演绎思维对归纳结果进行验证、证明，还发展了学生的理性精神和科学精神。当然，数学思维的发展应贯穿于个体数学学习的全过程、全阶段，甚至人的一生。希望本文对归纳思维的理论分析和实践探索能给广大数学教育工作者带来一些启发。