由稳定流形和不稳定流形证实氢原子的粘性效应
2023-04-29刘照军王丁薄文静王培杰
刘照军 王丁 薄文静 王培杰

摘要:本文研究了氢原子哈密顿系统暴露在强激光场下的粘性效应,即使对于单电子系统,其庞加莱截面也显示出了由激光场引起的混沌部分和规则部分,并可以用KAM理论来解释.通过变分方法对混沌“海”中的不稳定周期軌道进行了寻找,并数值求解了相应的稳定流形和不稳定流形.研究结果表明,单电子系统电离的动力学性质由不稳定周期轨迹控制.一方面,不稳定周期轨迹的稳定流形很好地与递归图叠加在一起,表明稳定流形只与相空间中稳定的初始点重叠.另一方面,不稳定流形几乎与庞加莱表面上密集分布的点重合.这表明不稳定流形只是通过激光场驱动轨迹演化的电离通道.此外,在稳定流形与不稳定流形相互穿插的不稳定岛附近的不同区域的存活概率也被深入研究.它们服从代数衰减规律.相同的衰减趋势也出现在不稳定流形上,它们具有与不稳定周期轨迹附近区域相近的衰减参数.这些观察证实了不稳定周期轨迹的稳定性对在KAM稳定岛附近相空间的粘滞效应起着非常重要的作用.
关键词:光电离;粘性;不稳定周期轨迹;稳定流形;不稳定流形
收稿日期: 2023-10-03
基金项目: 国家自然科学基金面上项目(21872097)
作者简介: 刘照军(1966-),男,河南南阳人,博士,教授,研究方向为原子分子物理和分子光谱学理论和应用.
E-mail: liuzhaojun@tsinghua.org.cn
通讯作者: 王培杰. E-mail:pjwang@cnu.edu.cn
The stickiness effect of hydrogen atom
evidenced by stable and unstable manifolds
LIU Zhao-Jun1, WANG Ding2, BO Wen-Jing2, WANG Pei-Jie2
(1. Department of Physics, Luoyang Normal University, Luoyang 471934, China;
2. The Beijing Key Laboratory for Nano-Photonics and Nano-Structure,
Department of Physics, Capital Normal University, Beijing 100048, China)
In this paper, we investigated the stickiness effect of the Hamilton system of the Hydrogen atom exposed to intense laser field. Even for the one electron system, its Poincare surface of section shows the chaotic and regular parts due to the laser field which can be explained by KAM (Kolmogorov, Arnold, and Moser)theory. The unstable periodic orbit (UPO)in chaotic "sea" was located by variational method and the corresponding stable manifold (SM)and unstable manifold (UM)of the UPO were numerically calculated. It was shown that the dynamics of ionization of the one electron system is governed by the UPO. On one hand, the SM of UPO is well superposed with the recurrence plot, which indicates that the SM overlaps just the stable initial points in phase space. On the other hand, the UM is almost coincide with the densely distributed points on Poincare surface of section. This indicated that the UM is just the ionization channels of the trajectories driven by laser field. Furthermore, the survival probabilities of different regions which gradually cross the UM and SM tangential flow nearby the stable island are studied. They obey an algebraic decaying law. The similar decay trend are also observed on different regions on the UM which possess almost the same decay parameters with that of region nearby the UPO. These observations confirmed that the stability properties of UPO play very important role in the stickiness effect of the phase space nearby the KAM stable islands.
Photo ionization; Stickiness; Unstable periodic orbit; Stable manifold; Unstable manifold
1 Introduction
The phenomenon of recurrence, introduced by Poincare[1, 2], has attracted much intention over the last three decades in the theory of nonlinear dynamics [3-6]. The nonlinear Hamiltonian systems usually present phase space composed of a coexistence of regular and chaotic orbits[7]. With the increasing of the nonlinearity by energy or by external perturbation, the quasi-periodic orbits would be destructed to zero measure according to KAM theorem[8-12]. And the related phase space would undergo from regular to chaotic structures. The destruction of quasi-periodic, periodic orbits, and regular structures in phase space is a gradual process. During this process the regions of regular motion are formed by complex structure of KAM islands. Then, the stickiness of the trajectories to regular regions takes place, and the recurrence time probability (defined as the probability of a trajectory to return at time t to a pre-defined region)or the survival probability (defined as the probability of a trajectory to be ionized at time t)is believe to decay algebraically:
P(τ)~t-α(1)
This algebraic decay was first observed by Channon and Lebowitz[13]. Then Venegeroles reported the universality of algebraic laws in Hamiltonian systems where the decay of recurrence time statistics (α), and superdiffusion (β), satisfies the relation α+β=3, consequently, the algebraic decay of the recurrence distribution and anomalous diffusion are two sides of one coin[3, 7]. Taline group studied how hyperbolic and nonhyperbolic regions in the neighborhood of a resonant island perform an important role allowing or forbidding stickiness phenomenon around islands in conservative systems [14]. Stickiness was also studied using finite time Lyapunov exponents and the results showed that the distribution of the finite time Lyapunov exponents was bimodal due to orbits sticking near elliptic regions [15].
Despite significant progress made with these theories, the understanding of algebraic decay equation (1)by sticky effect from the simple Hydrogen atom exposed to intense external laser field is still very limited. Different from the map and conservative systems, this system is open system in which energy is not conservative due to the external laser field perturbation. The sticky effect forces a trajectory injected into the boundary area to stay near the boundary for long periods of time. Therefore, one of the main consequence of this phenomenon is that for non integrable systems, there exists a survival time distribution with long-term algebraic decay. In this paper, we investigated the sticky effect of Hydrogen atom exposed to external laser field and showed that the stickiness is associated with the presence of injection channels related to the crossing of stable and unstable manifolds of unstable periodic orbit.
This work is organized as follows: in Chapter 2 we focus our attention on the model and stabilization effect. In Chapter 3 we develop our main results concerning the effect of the (non)hyperbolic surrounding of resonance island in the dynamics of the system. Our conclusions are presented in Chapter 4.
2 The defined model and the stabilization
2.1 The Hamiltonian of the system
We consider the classical model for Hydrogen atom interacting with an intense linearly polarized laser field in the dipole approximation. The Ha-miltonian of the system in one dimension (1D)can be expressed as the followings equation:
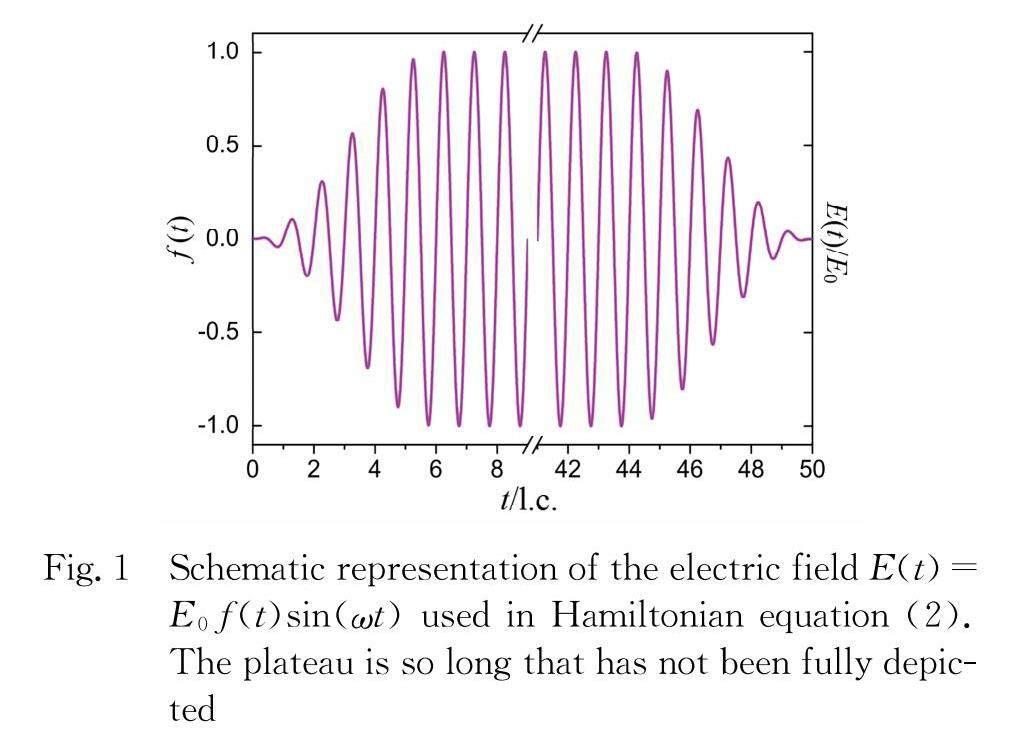
Here,pxis the momentum of the electron canonically conjugate to the position x along the polarization axis;E0is the amplitude of the electric field;f(t) is the pulse envelope (schematically represented in Fig.1);ω is the frequency of the laser which is chosen as 0.8 a.u. corresponding to a wavelength of 57 nm laser throughout this paper. We have chosen a soft Coulomb potential[16]as the interaction potential between the electron and its parent ion. The soft Coulomb potential parameter is set as 1.
2.2 Ionization probability stabilization
We recall the numerical experiment result in Ref.[17] which hints the stabilization of the ionization of Hydrogen atom exposed to the external laser field. For the envelope function f(t), we select a smooth turn-on consisting of a linear ramp-up of duration Tu=6T, a plateau of Tp=44T, and a linear ramp-down of duration Td=6T, where T=2π/ω is the period of the laser. All the initial conditions just are from ground state of the Hamiltonian (2)and uniformly distributed in phase space (x,p) for|x|<10. For calculating the ionization probability, we use a distance criterion for ionization which the chosen threshold is 50 a.u.. The ionization curve is shown in Fig.2 where the ionization probabilities as functions of E0(in atomic units a.u.)obtained for Hamiltonian (2)with a linear ramp-up of duration Tu=6T, a plateau of duration Tp=44T and a linear ramp-down of duration Td=6T.
Here we qualitatively reproduced the results obtained in reference[17], where the ionization at very high intensity and the global decrease of the ionization probability as the intensity of the laser field is increased (see Fig.2). It is just the stabilization phenomenon induced by intensity of laser field which has been reported by our previous work[18]. It is demonstrated in the paper that the stabilization of atom in a strong laser field is dri-ven by a set of periodic orbits.
3 Results and discussion
3.1 The recurrence properties imprinted by the SM
For the recurrence properties of the Hamiltonian (2)during the plateau (here set the envelope function f(t)=1), we evolved its equations of motion by selecting the initial points in phase space where coordinates ranges are as x(-3,3), px(-2.25, -2.75)by Runge-Kutta method[19]. Then we record the number of times which the initial points return to the small window in the Poincare surface of section (stroboscopic plot with period T). The small window in Poincare surface of section is set as x(-50, 50) (50 a.u. is the distance criterion for ionization)to ensure that the electrons are not ionized by the laser field. The recurrences plot in phase space at final integrating time as shown in Fig.3. The different colours demonstrates the times of the initial points in phase space return to the Poincare surface of section. Here the laser intensity is set as E0=1.8 and the total integrating time is set as 100 laser periods.
Fig.3 shows very regular pattern which has two big regular island regions. The boundary of the two stable regions are becoming obscure which indicating the escaping of the electron from the regular region leading to the ionization. The further the regions, the deeper the colours. This hints that more trajectories do not return back to the defined Poincare surface of section. By the smooth outlines of the regular regions, they hint the relation to the stable manifolds of some unstable periodic orbit. We recall the conclusion in our previous paper[18]that the dynamics of the Hamiltonian (2)was govern by the periodic orbits. With the increase of the nonlinearity of system, the periodic orbits would bifurcate and the KAM tori would be destroyed. Then the total phase space become chaotic even to ergodic. Even the total measure of period orbits is approaching to zero. For the phase space of Hamiltonian (2), there are three periodic orbits of particular interest and organize the dynamics (they are all shown in Fig.3 denoted by star symbol for the unstable periodic orbit O and white circle symbol for the two stable periodic orbits O+, O-). It is noted that the two stable periodic orbits O+, O-are located in the center of two big regular islands while the unstable period O is located in the middle of the two big regular islands which is the separatrix and the saddle point. In fact, as laser intensity E0is small, the Hamiltonian (2)is almost integrable, and the periodic orbit is elliptic and it would undergoes a pitchfork bifurcation with E0increasing at a critical value. Then the orbit O turns hyperbolic and two asymmetric and elliptic periodic orbits are created as O+, O-). So, the unstable periodic orbit plays very important role on the dynamics of Hamiltonian (2). So does its manifolds.
Here we characterize a hyperbolic region of the phase space as an ensemble for which the tangent phase space splits continuously into SM and UM. SM and UM are invariant under the system dynamics: infinitesimal displacements in the stable (unstable)direction suffer exponential decay as time goes forward (backward)[20]. We calculated SM and UM of the unstable periodic orbit O by numerical method [21].
As shown in Fig.5 and Fig.4b, the SM (by orange colour line)and UM (by red line)of UPO O are completely symmetric with the x=0 axis. The homoclinic tangles by SM and UM cross nearby of the UPO with infinite times. The stable manifold of the UPO are also demonstrated in Fig.3. The outline and the lateral boundary of the recurrence plot is perfect superposed. This hint the dynamics of recurrence near the regular island is controlled or depicted by the SM of the UPO.
3.2 The escaping channel of UM
For the initial points [x=(-1.69,0), px=-2.41], the evolving time is set as 300 laser periods, then we recorded the Poincare surface of section (stroboscopic plot with period T)as shown in Fig.4 by blue dot symbols. It is interesting that the densely distributed points of Poincare surface of section are imprinted just by the traces of UM. We also confirmed that with different evolving time, the initial points would be driven by laser to escape from the regular region gradually just along the flows of the UM of UPO. This also could be clearly observed by Fig.4d where the initial points is in the left regular island. With the time evolving under the laser field, the trajectories would evolving along the paths of UM to the periphery of right regular island. This observation demonstrates that the UM of UPO O is the channel of the ionization of the trajectories! At least it is the ionization channel of the initial points which near the regular island.
3.3 The stickiness effects
From Fig.3, it is clearly hinting that the manifolds tails embrace the stable recurrence islands, hence it may also associates with the stickiness effect of the trajectories near the regular islands centered by two asymmetric and elliptic periodic orbits. The stickiness effect of the phase space can be demonstrated by the recurrence time probability defined by equation (1).
Firstly, we investigated the stickiness effect of the region nearby the stable island with different laser intensities (It is not clear in the text how these curves are computed. As can be seen later, it depends on the chosen initial conditions. Is it for the initial condition of Sec.3.2? The Cristel comment is reasonable, we should selected the initial points with similar standard.). As shown in Fig.6, by changing the intensity from 1.8 a.u. to 2.0 a.u. and 2.6 a.u., the survival probabilities decay with time (here the unit of time is laser cycle (l.c.))by algebraic law. The corresponding fitted parameters α are 1.56, 2.38 and 2.14. This means that the stickiness effect is most stronger for the selected initial points nearby the stable region when the intensity of laser is at about 2.0 a.u.. As we recalled the maximum eigenvalues of monodromy matrix[22]associated with O as a function of E0(refer the Fig.4 of Ref. [18])has a maximum value as E0=2.0. So both of the stickiness effect and the maximum eigenvalues of monodromy matrix associated with UPO O correlated to each other. The both trends with the increase of the nonlinearity induced by laser are just coincident. This indicates that the local properties of stickiness effect of phase space nearby the stable island just associated with the stabilization of UPO.
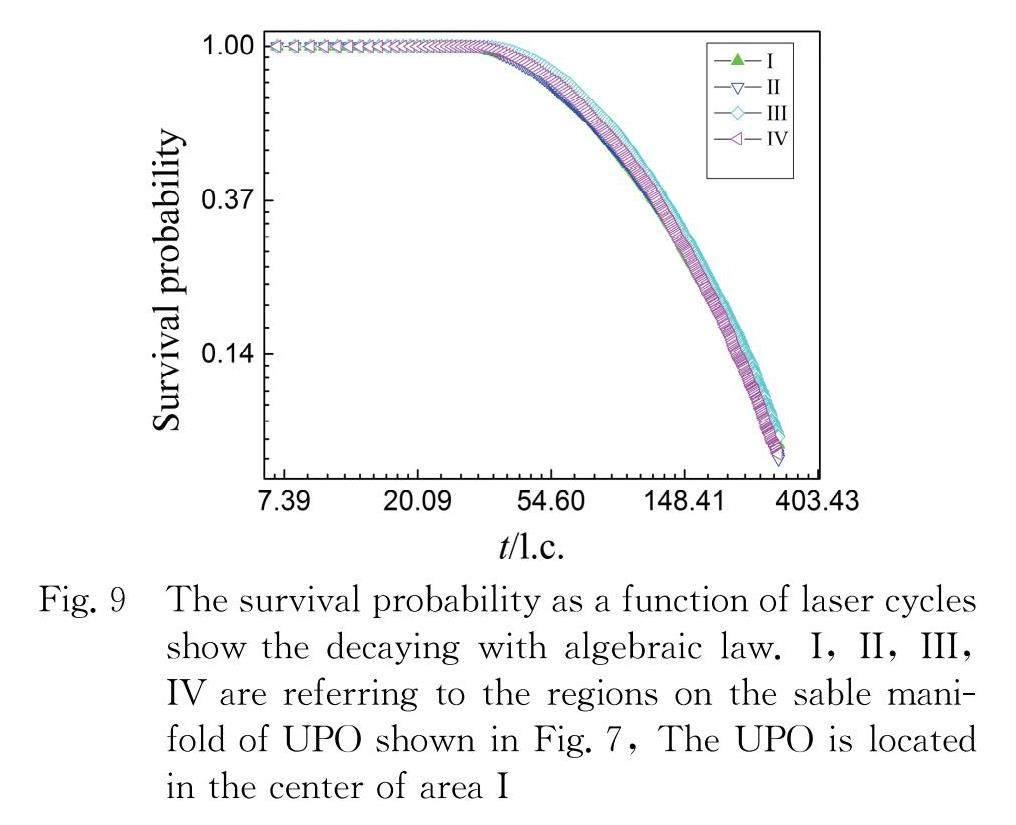
For the local properties of stickiness, we selected the initial conditions of the regions nearby the regular island as shown in Fig.7. The regions of small rectangles labeled as a,b,c,d,e,f,g were selected as observed initial points. The related survival probabilities as function of time is shown in Fig.8. The corresponding parameters α are 10.28, 1.67, 1.85, 1.79, 1.26, 0.04 and 0. The bigger the parameter α, the faster the survival probability decaying. As the regions adjoin to the regular island, the stickiness is increasing. For
the region a, the decaying parameter is bigger than 3 which contradict with the conclusion of the relation α+β=3[3]. The reason is the fact that configuration space (x) is unbounded in this system. For the region e, which was mostly overlapped by stable manifold, the parameters α proximately equal to 1.3 and the stickiness effect is prominently! This stickiness effects are globally spread by the stable manifold of UPO. If we selected smaller region just on the SM overlapping area as shown in Fig.7 I, II, III, IV, here the region I embrace the UPO in phase space. Then the global properties of stickiness by SM are shown in Fig.9. The similar trend of decay of survival probabilities (the parameter α approximately equals to 1.41)indicates that the SM of UPO do play very important role for the escaping of the trajectory away from the regular island.
4 Conclusions
In summary, we investigated the stickiness effect of 1D hydrogen atom exposed to intense laser field. It is demonstrated that the UPO plays crucial role in governing the ionization dynamics of the hydrogen atom. Its UMs are well superposed the densely distributing points of the Poincare surface of section. It was confirmed that the UMs are the channels of ionizing of the trajectories nearby the stable region. We also observed that the well superposed phenomena of the SM with the recurrence plot of the Hydrogen atom system. This indicated that the stickiness effects of the trajectory nearby the regular island are dominated by the SM of the UPO. Further investigating the survival probabilities of different regions in phase space as a function of laser cycles revealed that the stickiness effects of the regions nearby the regular island obey the algebraic law. The local and global properties of stickiness associated with the SM of UPO are also discussed. However, the more interesting phenomena associated with stabilization of Hydrogen atom exposed to external intense laser field need to be investigated. How stickiness effect behave in quantum mechanics of Hydrogen atom? What is the quantum correspondence of the SM and UM of the UPO? These topics would be our next research.
References:
[1]Poincare H. On the three-body problem and the equations of dynamics [J]. Acta Math, 1890, 13: 1.
[2]Frisch H L. Poincar recurrences [J]. Phys Rev, 1956, 104: 1.
[3]Venegeroles R. Universality of algebraic laws in Hamiltonian systems [J]. Phys Rev Lett, 2009, 102: 064101.
[4]Altmann E G, Motter A E, Kantz H. Stickiness in Hamiltonian systems: from sharply divided to hierarchical phase space [J]. Phys Rev E, 2006, 73: 026207.
[5]Altmann E G, Tel T. Poincar recurrences and transient chaos in systems with leaks [J]. Phys Rev E, 2009, 79: 016204.
[6]Meiss J D. Thirty years of turnstiles and transport [J]. Chaos, 2015, 25: 097602.
[7]MacKay R S, Meiss J D, Percival I C. Stochasticity and transport in Hamiltonian systems [J]. Phys Rev Lett, 1984, 52: 697.
[8]Altmann E G, Endler A. Noise-enhanced trapping in chaotic scattering [J]. Phys Rev Lett, 2010, 105: 244102.
[9]Bernal J D, Seoane J M, Sanjuan M A F. Weakly noisy chaotic scattering [J]. Phys Rev E, 2013, 88: 032914.
[10]Gutzwiller M C. Chaos in classical and quantum mechanics [M]. New York: Springer Science and Business Media, 2013: 116.
[11]Ott E. Chaos in dynamical systems [M]. Cambridge: Cambridge University Press, 2002: 160.
[12]Kruscha A, Ketzmerick R, Kantz H. Biased diffusion inside regular islands under random symplectic perturbations [J]. Phys Rev E, 2012, 85: 066210.
[13]Channon S R, Lebowitz J L. Numerical experiments in stochasticity and homoclinic oscillation [J].Ann Ny Acad Sci, 1980, 357: 108.
[14]Kruger T S, Galuzio P P, Prado T L, et al. Mechanism for stickiness suppression during extreme events in Hamiltonian systems [J]. Phys Rev E, 2015, 91: 062903.
[15]Szezech J D, Lopes S R, Viana R L. Finite-time Lyapunov spectrum for chaotic orbits of non-integrable Hamiltonian systems [J]. Phys Lett A, 2005, 335: 394.
[16]Becker W, Liu X J, Ho P J, et al. Theories of photoelectron correlation in laser-driven multiple atomic ionization [J]. Rev Mod Phys, 2012, 84: 1011.
[17]Grobe R, Law C K. Stabilization in superintense fields: a classical interpretation [J]. Phys Rev A, 1991, 44: R4114.
[18]Norman M J, Chandre C, Uzer T, et al. Nonlinear dynamics of ionization stabilization of atoms in intense laser fields [J]. Phys Rev A, 2015, 91: 023406.
[19]Ascher U M, Ruuth S J, Spiteri R J. Implicit-explicit Runge-Kutta methods for time-dependent partial differential equations [J].Appl Numer Math, 1997, 25: 151.
[20]Guckenheimer J, Holmes P. Nonlinear oscillations, dynamical systems, and bifurcations of vector fields [M]. New York: Springer Science and Business Media, 2013: 227.
[21]Hobson D. An efficient method for computing invariant manifolds of planar maps [J].J Comput Phys, 1993, 104: 14.
[22]Cvitanovic P, Artuso R, Mainieri R, et al. Chaos: classical and quantum [M]. Nelson: Niels Bohr Institute, 2010.
引用本文格式:
中 文: 刘照军, 王丁,薄文静, 等. 由稳定流形和不稳定流形证实氢原子的粘性效应[J]. 四川大学学报: 自然科学版, 2023, 60: 064002.
英 文: Liu Z J, Wang D, Bo W J, et al. The stickiness effect of hydrogen atom evidenced by stable and unstable manifolds [J]. J Sichuan Univ: Nat Sci Ed, 2023, 60: 064002.
