类别型缺失数据的聚类半参数logistic学习插补法
2023-04-29夏怡凡陈玉邹普越
夏怡凡 陈玉 邹普越
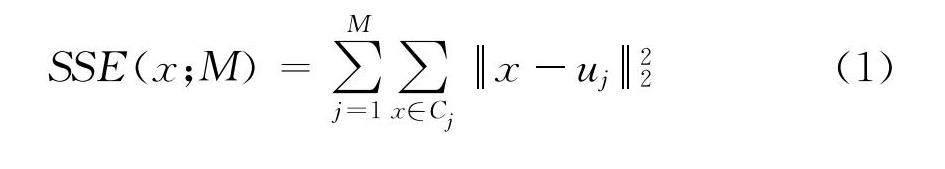
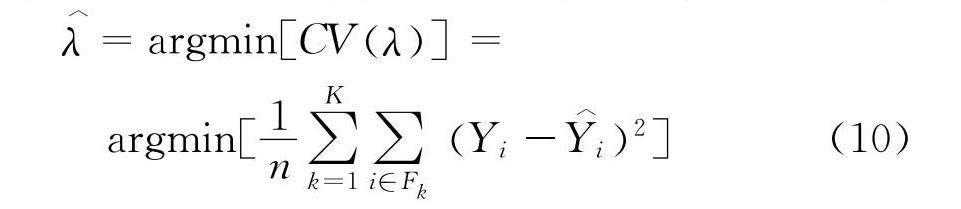

摘要:缺失数据插补是数据科学中的基本方法之一. 本文针对类别型缺失数据提出了一种基于聚类和半参数logisitic学习模型的插补法. 该方法首先采用K-近邻法对缺失数据进行预插补,然后用聚类算法将数据分类,提高数据间的相似性,再为每一类数据集建立半参数logistic学习模型,进而完成最后的插补. 基于中国家庭金融调查(CHFS)数据集的实证研究表明,该方法优于常用的K-近邻插补法和随机森林插补法.
关键词:类别型缺失数据; K-means聚类; 半参数logisitic学习模型; 缺失数据插补
收稿日期: 2023-05-16
基金项目: 国家社会科学基金(16BTJ013)
作者简介: 夏怡凡,男,教授,博士生导师,主要研究方向为多元统计与数据融合. E-mail: xiayifan@swufe.edu.cn
A clustering semi-parametric logistic learning inputation method for categorical missing data
XIA Yi-Fan1, CHEN Yu1, ZOU Pu-Yue2
(1. School of Statistics, Southwestern University of Finance and Economics, Chengdu 611130, China; 2. SWUFE-UD Institute of Data Science at SWUFE, Southwestern University of Finance and Economics, Chengdu 611130, China)
Missing data interpolation is a basic method in data science. In this paper, we introduce a new method for categorical missing data based on the clustering and semi-parametric logistic learning model. Firstly, the K-nearest neighbor method is used for the pre-interpolation of missing data. Then the data are classified into related clusters with the K-means clustering method. Finally, the semi-parametric logistic learning model is established for each cluster to complete the interpolation. The simulation based on the China Household Finance Survey (CHFS)dataset exemplify the superiority of new method compared with the classic K-nearest neighbor method and the random forest interpolation method.
Categorical missing data; K-means clustering; Semi-parametric logistic learning model; Missing data interpolation
1 引 言
随着大数据及人工智能技术的快速发展,数据发挥着越来越重要的作用. 然而,在生产实践中,数据往往存在着缺失问题,降低数据的价值. 正因如此,对数据缺失问题的研究成为统计学中的一个热点.
数据缺失的原因众多,有些是因为数据记录工具故障,有些是因为在调查过程中被访者无回应,有些则是因为跟踪样本丢失. 为便于研究,学界一般将数据缺失模式分为单变量缺失和多变量缺失,其中多变量缺失模式又可以进一步细分为单调(Monotonic)缺失和一般(General)缺失. 从缺失机制看,数据缺失可分为完全随机缺失(Missing Completely at Random,MCAR)、随机缺失(Missing at Random,MAR)及非随机缺失(Not Missing at Random,NMAR). 一般而言,实际应用中的数据缺失问题大多数属于多变量、非随机缺失,而只有在非随机缺失情况下数据插补问题才有研究的必要.
对数据缺失问题进行处理主要有事前预防和事后补救两大类方法. 从实际应用出发,事后补救法是研究的主流. 1940年,Stephan等[1]提出了抽样概率的倒数加权法. 1944年,Deming[2]在误差因素分析基础上总结了前人对数据缺失问题的研究,指出调查研究中的偏差主要源于数据缺失. Yates[3]针对实验数据中缺失数据较多的问题提出了一种插补方法,并发展出均值插补法、冷卡插补法、回归插补法、热卡插补法、多重插补等方法. 1963年,Bltekjaer等[4]研究了冷卡插补法在调查研究缺失数据集上的插补效果. 1977年,Dempster等[5]提出了期望极大化算法(EM算法),并将其应用于缺失值插补,这是对传统插补法的颠覆性创新,是缺失数据处理研究的一个里程碑. 1978年,Rubin等[6]认识到单值插补的缺点,提出了填充效果更好的多重插补法. 1984年,Kalton等[7]吸收了热卡法的思想,创造性地提出了K-最近邻插补法,有效解决了热卡插补法的缺点,并影响到后来的缺失插补方法研究.
进入二十一世纪后,越来越多的研究将机器学习模型和深度学习模型应用于数据缺失处理. 例如,Batista等[8]对机器学习的四种缺失数据处理方法进行了分析比较,发现K-最近邻插补算法在四种模型中具有天然的优越性. 2006年,Gan等[9]针对基因表达数据中存在的缺失问题提出了一种基于凸集投影的理论框架,用于缺失数据插补. 2018年,Noor等[10]利用环境科学领域收集到的环境温度和湿度监测数据评估了均值填充、回归填充、多重填充和最近邻填充的效果. 2000年,金勇进等[11]通过模拟实验对几种缺失值插补方法进行了比较,结果表明均值填充更符合真值,而随机回归插补则更能保持样本分布. 2005年,茅群霞[12]重点研究了多重插补法在缺失值问题下的应用. 2007年,张宏亭等[13]提出了使用神经网络插补缺失值的方法,并将其应用于飞机真实数据处理,结果表明神经网络插补法能有效解决特定场景下的记录数据缺失问题. 此后,邓银燕[14],石丽[15]及罗永峰等[16]分别研究了均值插补、随机插补、期望最大化(EM)插补、线性回归模型插补、多重插补等缺失数据插补方法. 2013年,张婵[17]采用支持向量机回归理论分别对连续型、类别型缺失数据进行了预测. 2014年,孟杰等[18]将随机森林模型引入调查问卷缺失数据的插补. 2015年,庞新生等[19]将半参数回归模型与插补方法相结合,利用最小二乘核估计构建半参数模型,再利用辅助变量对目标变量进行估计来建立缺失数据的插补数据集,实现缺失数据插补. 2019年,蒋辉等[20]提出了基于朴素贝叶斯和EM算法的交替迭代的插补方法. 2021年,熊中敏等[21]对近年来国内外的缺失数据处理方法进行了综述,总结了各自的优缺点、适用范围、效果评价指标.
此外,半参数方法也被应用于数据插补研究. 特别地,针对被解释变量因受某种随机干扰而被右截断的情形,王启华[22]对半参数模型的相合性进行了讨论. 针对响应变量存在缺失的半参数回归模型,范承华等[23]对未知参数构造了经验对数似然比统计量,并与最小二乘法进行了优劣比较. 裴晓换[24]则对随机缺失和固定设计下的半参数回归模型进行了估计,在较弱的条件下证明了参数向量、非参数部分及误差方差的强相合性.
总的来看,目前对半参数方法应用于数据插补的研究还比较少,且大多集中于随机缺失模式,对非随机缺失数据的插补问题,即利用变量间的相关性进行插补的研究更少. 本文将运用半参数方法研究非随机缺失数据的插补问题.
后文的安排如下. 在 第2节中,我们将基于快速聚类和半参数logistic学习模型建立新的缺失值插补法(后文简称新方法). 我们在第3节讨论新方法的效果和性质. 在验证新方法的有效性后,第4节中我们将该方法用于解决全国家庭金融调查(CHFS)中的缺失数据插补问题. 第5章是结论与展望.
2 基于聚类和半参数logistic学习模型的插补法
针对非随机缺失机制的不完全数据集,本文提出一个适用于类别型单变量缺失情形的基于半参数logistic模型的缺失数据两阶段插补算法.
第一个阶段是数据预处理和聚类阶段,主要流程是数据预插补和样本聚类. 首先,将含有缺失值的原始不完备数据集划分为两个独立数据集,一个是不含缺失记录的完整数据集(D1),另一个是含有缺失值的缺失数据集(D2). 对完整数据集(D1)进行相关性分析后,以完整数据集训练K-最近邻插补算法进行训练,之后将训练完毕的K-最近邻插补算法应用于缺失数据集. 同时,对缺失数据进行第一次插补(也称为预插补),预插补可以大大减少各变量相关系数的估计误差. 其次,待预插补完成后,选择高效率和适用性广的K-means聚类算法将初步得到的完备数据集划分为M个数据聚类C1,C2,…,CM,同一数据聚类中的样本具有高相似度,不同数据聚类之间的样本的相似度则较低.
第二阶段为半参数logistic学习和插补阶段,主要流程是完成半参数logistic学习模型的参数估计后利用其对缺失数据集(D2)进行再次插补. 根据第一阶段得到的M个聚类C1,C2,…,CM,每个聚类一般既包含完整数据集(D1)中的部分样本,也包含缺失数据集(D2)中的部分样本(若某类中不含D2的样本,则不进行插补). 在每一个数据聚类中建立半参数logistic学习模型,把自变量划分为线性部分和非线性部分,然后利用该数据聚类中属于完整数据集的数据样本通过迭代法估计半参数logistic学习模型参数,最后利用训练完毕的半参数logistic学习模型对该数据聚类内的属于不完整数据集的样本进行缺失值插补.
综上,基于半参数logistic学习模型的类别数据插补法的核心思想是:将缺失值的插补从大范围慢慢缩小到若干个小范围,然后在小范围内利用半参数模型准确地进行缺失值插补,类似于近似逼近.
类别缺失值插补算法的流程如下.
(1) 将数据集D划分为D1和D2,D2有缺失数据,D1不含缺失数据.
(2) 区分变量. 进行因变量和自变量的线性相关性分析,相关性较强的变量纳入半参数模型的参数部分,较弱的变量纳入半参数模型的非参数部分.
(3) KNN预插补.
(4) K-Means聚类. 通过下述的公式(1)和(2)形成C1,……,CM数据聚类. K-means聚类是一种快速聚类方法,该算法通过计算数据之间的距离来对样本进行分类. K-means算法的目标是在已知样本分M类的条件下最小化平方误差
其中uj是数据聚类Cj,j=1,2,…,M的均值向量,有时也称为质心,表达式为
因问题(1)的求解是一个NP难问题,K-means聚类算法采用贪心策略,通过迭代优化来近似求解问题(1)(2),具体执行过程如下. 首先,选取M个数据聚类的初始聚类中心点,计算数据集中的其他数据对象与各数据聚类中心点间的距离,并按照最小距离原则对样本进行分类. 然后,更新每个类的聚类中心点,再对整个数据集中的数据重新划分所属聚类,重复上述步骤,直至各类的聚类中心点不再变化,算法终止执行.
(5) 半参数logistic学习模型线性部分估计.如式(3)所示,本文建立的模型包括线性部分和非线性部分:
初始化非线性部分后,可以把非线性部分视为常数项,利用Adaptive Lasso和交叉验证对半参数logistic学习模型线性部分进行参数估计,Lasso方法的参数估计式为
其中λ为调和参数. 由(4)式可知,Lasso估计对于每一个待估计参数βj,j=1,2,…,p给予相同的惩罚权重. 值得注意的是,已有改进的Lasso估计方法出现,如Zou提出的改进Lasso,即Adaptive Lasso. 具体到模型(3),Adaptive Lasso方法的参数估计式为
进而,β的估计值可以写成
利用Adaptive Lasso进行参数估计时,调和参数λ的选择至关重要. 常用的选择方法有交叉验证(Cross-Validation)、广义交叉验证(Generalized Cross-Validation)及BIC准则(Bayesian Information Criterion)等. 本文将使用交叉验证选择调和参数λ,具体算法如下:
(i) 将数据集随机等分为K个子集,F1,…,FK;
(ii) 将其中一个子集作为验证集,其他子集作为训练集,对于调和参数λ的每一个取值计算模型在验证集上的误差
(iii) 对于调和参数λ的每一个取值,计算在所有验证集上的平均误差
显而易见,使交叉验证值CV达到最小的调和参数为最优的调和参数λ,最优的调和参数λ可由下式得到:
(6) 半参数logistic学习模型非线性部分估计.如式(3)所示,其中因变量Y取值为0或1,线性部分自变量为X=(X1,X2,…,Xp),非线性部分自变量为S=(S1,S2,…,Sq),线性参数部分有待估计参数β=(β1,β2,…,βp)′. 假设选定的三次样条基为B1,B2,…,Bj+4,那么三次样条函数的表达式为
其中参数θj可以通过极小化下式求解:
以具有两个节点(t1,t2)的三次样条模型为例,非线性关系的样条估计为如下线性回归模型:
在本文的模型中,非线性部分考虑形式(15)的可加模型, 即
利用三次样条估计模型中的非参数部分M(S),对于任意的i=1,2,…,q,存在如下转换:
其中l为节点数,通常设定为2,故可加模型M(S)可以由下式得到:
此时,对于非参数部分的估计已经不成问题. 值得注意的是,之前由式(7)估计得到的参数βj在本节中视为常数项,此时半参数logistic学习模型中的非参数部分如式(17)所示,参数θij,i=1,2,…,q,j=1,2,…,l+4可由最小化下式得到:
其中调和参数λ′可通过交叉验证选择最优λ′.
非参数部分MSα在第k+1次的估计为
重复步骤(5)(6),直至M(S)和β收敛,得到最终的参数估计值.
3 评价标准与仿真分析
要评价缺失值插补算法的好坏,必须对缺失值插补的有效性进行评价.下面我们给出缺失值插补有效性的评价标准.
假设Y为原始真值数据,?为根据插补模型插补的数据,n为缺失数据总数. 由于本文的研究对象为类别型缺失变量,为了使后续数据分析结论更准确可信,本文借鉴Breiman提出的算法思想,利用预测精度来衡量插补效果,即将缺失值插补算法在缺失数据集上的分类错判率作为插补有效性和可信度的评价标准,缺失值插补算法在缺失数据集上的分类准确率越高,插补的效果越好,可信度越高,分类准确率(Accuracy)定义如下:
该指标的取值在0~1之间,若指标值等于1则说明该变量被完全插补正确.
为进行仿真,我们选用半参数线性函数
Zi=β0+β1X1+β2X2+…+βpXp+MS1+MS2+…+MSq+ε,
其中β0,β1,β2,…,βp为半参数模型的参数部分,X1,X2,…,Xp为半参数线性函数参数部分的自变量,MS1,MS2,…,MSq为非参数部分的表达式,参数部分的自变量
Xm~N0,Σ,m=1,…,p,Σ(i,j)=r|i-j|,
这里取r=0.5. 设置非线性部分的解释变量Sj为[0,1]区间上连续的随机变量,ε为随机误差,服从正态分布,即ε~N(0,1).
总量为n的样本的产生过程如下所示. 给定p+1个随机数,依次赋值给β0,β1,β2,…,βp.生成n个p维正态分布的随机数,依次赋值给(xi1,xi2,…,xin),i=1,2,…,n. 生成n个服从N(0,1)的随机数,依次赋值给ε1,ε2,…,εn. 非线性部分考虑不同的表达式下的模拟情况. 计算函数值
zi=β0+β1xi1+β2xi2+…+βpxip+Msi1+Msi2+…+Msiq+εi
及其中位数zme. 对于i=1,2,…,n,当zi≥zme时,yi=1;当zi
在本文中,我们用众数插补法、K-近邻插补法和随机森林插补法作为对比. 为了图表简洁,本文用Mode代表众数插补法,KNN代表K-近邻插补法,RF代表随机森林插补法,K-SemiLR代表本文提出的插补方法.
根据已有的研究可知,在同一插补方法下不同的样本量和不同的数据缺失比例会影响插补模型的有效性. 因此,本文的仿真将考虑样本量n分别为2000、3000、5000时数据缺失比例ROM (Rate of Missing)分别为10%、20%、30%和50%的情况下各插补模型的效果,并给出不同线性参数值、不同非线性部分表达式下的仿真结果.
对于新方法中的参数估计问题,我们采用五折交叉验证. 我们用100次模拟结果的平均模型分类错判率作为评价插补模型估计表现好坏的指标,模拟结果保留4位小数,部分用到的参数和变动范围参见表1,调整参数的变化范围可以生成不同的数据集,用于检验缺失值处理方法的性能.
仿真结果参见表2~表4及图1.
仿真2的结果显示,在数据样本为2000、线性部分自变量维度p=9的条件下,本文提出的插补算法比KNN插补算法、众数插补算法及随机森林插补算法的准确率都高. 此外,综合仿真1和仿真2,考查相同的样本量、不同的线性部分维度下各个插补算法的仿真结果,我们有以下的结论.
(1) 若增加数据集中线性部分的维数,各插补算法的性能均呈下降趋势. 以本文提出的算法为例,在线性部分维数分别为6和9的仿真下,K-semiLR插补法在各个缺失率下的准确率分别为91.70%,89.63%,91.25%,89.55%和90.25%,91.60%,88.13%,88.20%,逐渐降低.
(2) 随着线性部分维数的增加,各插补算法性能的下降幅度存在差异,K-semiLR插补算法的性能下降幅度较小,优于随机森林插补算法,随机森林插补算法的性能下降幅度大,表明随机森林插补算法对高维数据的性能表现不稳定. 此外,另两种算法无论准确性和预测下降幅度都较差.
仿真3的结果显示,在数据样本为2000、非线性部分自变量维度q=3的条件下,在所有算法中K-semiLR插补算法的准确率最高. 综合仿真1和3,以及不同的非参数部分构成,对各类插补算法我们有以下的结论.
(1) 随着数据集中非线性部分复杂度的提高,各插补算法的性能呈现下降趋势. 以K-semiLR插补算法为例,在非线性部分表达式分别为
的仿真下,不同缺失率下的准确率分别为91.70%,89.63%,91.25%,89.55%和87.38%,87.18%,87.10%,88.20%,逐渐下降.
(2) 在算法的稳定性上,随着非线性部分复杂程度的提高,K-semiLR插补算法的波动幅度进一步收窄,其他插补算法的波动幅度则呈现扩大趋势,表明K-semiLR插补算法对于含有复杂非线性影响因素的缺失数据集有更好表现.
4 实证分析
本节中我们分析2017中国家庭金融调查数据集(China Household Finance Survey,SCHF)来比较K-semiLR插补算法与常用插补方法之间的性能.
CHFS由西南财经大学中国家庭金融调查与研究中心开发,每两年调查一次,形成一个大型问卷调查数据集. 调查属性包括人口统计学特征,资产与负债,保险与社会保障,支出和收入,金融知识基础治理与主观评价. 本文研究的数据来源于问卷中的家庭部分数据. 我们将对CHFS数据集中关于二胎意愿的缺失值进行插补.
选取其中涉及生育意愿的H3345问题、涉及医疗支出g1019_imp问题、涉及消费的g1011_imp问题以及涉及家庭经济情况的家庭金融资产问题(共7个变量). 二胎生育问题Y共有2个取值,其中A选项(取值为1,表示有二胎生育意愿)共1191个样本,B选项(取值为0,表示没有二胎生育意愿)共2812个样本. 为保证两类样本的均衡,我们采用欠抽样的方法得到平衡数据集,此时A选项和B选项的样本数均为1191,样本总数为2382.
此外,3个自变量X1、X2、X3与因变量Y的单因素logistic分析结果如表5所示.
在显著水平值0.05下,医疗支出和家庭资产呈现显著性,在后续基于聚类和半参数logisitic学习模型中我们将其作为线性部分. 另一方面,由于消费支出不呈现显著性,我们将其作为非线性部分. 采用节点数为5的三次幂基样条估计半参数logisitic学习模型的非线性部分,将M(S)化为线性形式,再采用Adaptive Lasso方法结合交叉验证,得到参数估计. 在不同缺失率(10%,20%,30%,50%)下,我们运用K-semiLR插补法,并采用五折交叉验证. 这样,我们建立半参数logisitic学习模型
在得到模型拟合估计后,我们将其应用于数据聚类内的缺失数据插补,结果见表7.
实证分析结果显示,在中国家庭金融调查数据集上考虑变量Y、X1、X2和X3,当缺失率分别为10%,20%,30%和50%时K-SemiLR插补算法均比其他插补算法的准确率高,次之是随机森林插补算法,而众数插补算法的插补值错误率最大,说明K-SemiLR插补算法对数据具有较好的还原能力.
5 结论与展望
针对类别型变量数据缺失问题,本文基于聚类和半参数logistic学习模型提出了一个新的缺失数据插补方法,该插补算法充分考虑数据集样本间的空间关系及样本属性间的线性和非线性关系. 插补算法由预插补-聚类阶段和半参数logistic模型插补两个阶段构成. 通过插补准确性的仿真,本文比较了K-SemiLR插补法与其他三种经典数据插补方法的正确率,证明本文提出的插补法对原始数据的还原能力优于众数插补法和KNN插补法,也略优于随机森林插补法,具有较好的插补准确性.
此外,实证研究显示,K-SemiLR插补算法的效果均优于众数插补法和KNN插补法插补法,这就验证了该模型在缺失数据上的有效性. 因此,我们认为,使用K-SemiLR算法插补类别型数据缺失值能够有效提高数据质量、提升调查研究精确度.
在后续研究中,我们将对以下两个问题进行进一步的探索:第一,采用其他聚类方法替代K-means聚类是否能显著改进插补算法准确率;第二,如何提高本文提出的插补算法的计算效率.
参考文献:
[1]Stephan F F, Deming H. The sampling procedure of the 1940 population census [J]. J Amer Stat Assoc, 1940,35: 615.
[2]Deming W E. On errors in survey [J]. Amer Soc Rev, 1944, 7: 359.
[3]Yates F. The analysis of replicated experiments when the field results are incomplete [J]. Empire J Exp Agr, 1933, 1: 129.
[4]Bltekjaer K, Malsnes B, Nordbotten A. An experimental investigation of transverse-wave interaction in periodic magnetostatic fields [M]. London: Macmillan Education, 1963.
[5]Dempster A P, Rubin N. Maximum likelihood from incomplete data via the EM algorithm [J]. J Royal Stat Soc Series B, 1977, 39: 1.
[6]Rubin D B, Service E T. Multiple imputations in sample surveys: a phenomenological Bayesian approach to nonresponse [C]// Alexandria V A. Proceedings of the survey research methods section of the American Statistical Association. Washington: American Statistical Association, 1978.
[7]Kalton G, Kish L. Some efficient random imputation methods [J]. Comm Stat, 2007, 13: 1919.[8]Batista G, Monard M. An analysis of four missing data treatment methods for supervised learning [J]. Appl Art Int, 2003, 17: 519.
[9]Gan X, Wee-Chung L A, Yan H. Microarray missing data imputation based on a set theoretic framework and biological knowledge [J]. Nucl Acid Res, 2006, 34: 1608.
[10]Noor N M, Zakaria N A. Imputation methods for filling missing data in air pollution data [J]. Urban Arch Const, 2018, 9: 159.
[11]金勇进, 朱琳. 不同差补方法的比较[J]. 数理统计与管理, 2000, 19: 5.
[12]茅群霞. 缺失值处理统计方法的模拟比较研究及应用[D]. 成都: 四川大学, 2005.
[13]张宏亭, 李学仁, 孔韬. BP神经网络在缺失数据估计中的应用[J]. 计算机工程与设计, 2007, 206: 3457.
[14]邓银燕. 缺失数据的填充方法研究及实证分析[D]. 西安: 西北大学, 2010.
[15]石丽. 多重插补在成分数据缺失值补全中的应用[D]. 太原: 山西大学, 2012.
[16]罗永峰, 叶智武, 郭小农. 钢结构施工过程监测数据缺失机理与处理方法[J]. 同济大学学报: 自然科学版, 2014, 42: 823.
[17]张婵. 一种基于支持向量机的缺失值填补算法[J]. 计算机应用与软件, 2013, 30: 226.
[18]孟杰, 李春林. 基于随机森林模型的分类数据缺失值插补[J]. 统计与信息论坛, 2014, 29: 86.
[19]庞新生, 李萌. 基于半参数模型的插补方法研究[J]. 太原师范学院学报: 自然科学版, 2015, 14: 1.
[20]蒋辉, 马超群, 许旭庆, 等. 仿EM的多变量缺失数据填补算法及其在信用评估中的应用[J].中国管理科学, 2019, 27: 11.
[21]熊中敏, 郭怀宇, 吴月欣. 缺失数据处理方法研究综述[J]. 计算机工程与应用, 2021, 57: 27.
[22]王启华. 随机截断下半参数回归模型中的相合估计[J]. 中国科学(A辑), 1995, 25: 819.
[23]范承华, 薛留根. 缺失数据下半参数回归模型的经验似然推断[J]. 应用数学, 2008, 88: 106.
[24]裴晓换. 带有缺失数据统计模型的估计和检验[D]. 西安: 西北大学, 2011.
引用本文格式:
中 文: 夏怡凡,陈玉,邹普越. 类别型缺失数据的聚类半参数logistic学习插补法[J]. 四川大学学报: 自然科学版, 2023, 60: 061001.
英 文: Xia Y F, Chen Y, Zou P Y. A clustering semi-parametric logistic learning inputation method for categorical missing data [J]. J Sichuan Univ: Nat Sci Ed, 2023, 60: 061001.
