基于GCN的复杂网络关键节点识别研究

杨洋 王俊峰

准确识别出网络中的关键节点是复杂网络研究的重要内容之一.现存的关键节点识别方法多数是基于网络结构提出的中心性度量方法，识别准确率低且适用范围具有局限性.因此本文提出了基于图卷积网络的关键节点识别方法，不仅考虑了节点属性，还考虑了网络结构和邻居节点结构.首先，根据网络图例数据提取多维度特征并构建特征向量;其次，将节点特征向量输入到GCN层学习;最后，通过回归损失函数计算出最小损失，识别出关键节点.本文选取传播动力学中的SIR模拟实验和牵制控制实验作为评价方式，在不同类型的真实网络上进行验证.结果表明本文提出的方法在适用范围和准确率方面较其他方法更具优势.

关键节点; 复杂网络; 图卷积网络

TP301.6A2023.032002

收稿日期： 2022-06-28

基金项目： 基础加强计划重点项目（2019-JCJQ-ZD-113）; 国家自然科学基金（U2133208）； 四川省青年科技创新研究团队（2022JDTD0014）

作者简介： 杨洋（1998-）， 河南平顶山人， 硕士研究生， 研究方向为网络空间安全. E-mail： 305004556@qq.com

通讯作者： 王俊峰. E-mail： wangjf@scu.edu.cn

Research on key node identification of complex network based on GCN

YANG Yang， WANG Jun-Feng

（College of Computer Science， Sichuan University， Chengdu 610065， China）

Accurately identifying the key nodes in the network is one of the important research topics in complex networks. Most of the existing key node identification methods are based on the centrality measurement method by the network structure， which has low identification accuracy and limited scope of application. A key node identification method， based on Graph Convolutional Network （GCN）， is proposed in this paper， which considers not only the node attributes， but also the network structure and neighbor node structure. Multidimensional features are extracted first from the network legend data to construct feature vectors and then the node feature vector is input to the GCN layer for learning. Finally， the minimum loss is calculated with the regression loss function， and the key nodes are identified. In this paper， SIR （Susceptible Infected Removed） is choosed as the evaluation method in the propagation dynamics simulation experiment and Pinning Control experiment， the proposed method is verified on different types of real networks， the results show that the GCN-based method proposed in this paper outperforms other methods in terms of scope of application and accuracy.

Key node; Complex network; Graph convolutional network

1 引 言

在网络理论的研究中，生物网络、电力网络以及通讯网络等都被证实为复杂网络［1］.关键节点［2］是能高度影响复杂网络功能的少数特殊节点.定位关键节点对网络信息传递、网络同步、网络控制起着至关重要的作用［3］.例如：社交网络中权威账号对舆论的引导作用明显;社会网络中控制流行病的爆发点能抑制传染病大规模传播;交通网络中挖掘关键枢纽能够为规划航线做出理论支撑［4］.此外，研究复杂网络中的关键节点在案件侦察、舆情控制等方面也有广阔前景［5］.

目前存在的关键节点识别方法是基于网络物理结构的中心性度量方法［6-8］，他们从网络的局部属性、全局属性、位置属性以及不同的随机游走策略4个方面度量节点的关键程度［9］.相关方法有：度中心性（Degree Centrality）算法、介数中心性（Betweenness Cen-trality）算法、K-Shell算法、PageRank算法等［10］.由于这些方法通常从单一角度寻找反映节点关键程度的因素，考虑得并不全面，且忽略了不同网络的结构差异性，导致识别准确率较低.

相关研究［9］表明，节点的关键性与多种因素有关，例如：网络的结构、节点的特征以及邻居节点间的结构.因此，对网络中多类信息进行融合分析能更准确地反映网络的真实情况，识别出关键节点.图卷积网络（Graph Convolutional Network， GCN）［11］是一种深度学习模型，由于它能够处理图形结构数据，且能研究网络拓扑中的节点和连边信息，因此已经成为处理复杂网络相关任务的有效方法之一［12］.对于关键节点识别任务， GCN能够迭代地聚集网络中节点及邻居节点间的结构信息，综合分析影响节点关键性的多种因素.

基于此，本文提出了基于GCN的关键节点识别方法.该方法从节点自身属性、复杂网络结构与邻居节点间的结构等三方面提取了7个具有代表性的特征，结合节点的二度子图进行分析.这些特征综合了网络局部属性、全局属性、位置属性以及随机游走属性，适用于不同类型的复杂网络［13-18］.此外，本方法还增加了节点的圈比［13］、桥接性［16］、节点嵌入［17］3个更具判别能力的特征，相较于单一特征工程方法［18］，特征维度更加广泛.本文在8个真实的复杂网络上对此方法进行验证，使用传播动力学中的SIR模拟实验和牵制控制实验作为评价方式［13］.在SIR模拟实验中平均感染率为其他方法的1.3倍;在牵制控制实验中牵制效率P的性能在36次实验中有34次排名第一，2次排名第二.实验结果表明，本文提出的方法在准确性和适用范围方面较其他方法更具有优势.

2 相关工作

基于中心性的关键节点识别方法［19］主要从复杂网络的局部属性、全局属性、位置属性以及随机游走四个方面进行研究.

（1） 局部属性. 基于网络局部属性的关键节点识别方法主要考虑了节点自身的属性及其邻居的相关信息，这些指标的计算复杂度较低，在结构复杂的大规模网络中使用广泛.度中心性算法［20］是网络中刻画节点关键程度最简单的指标，它通过节点度（与其相连的邻居节点数量）的大小来判断该节点的重要程度.在网络传播过程中，大度节点可以最大限度地传染它的邻居，也会以较大概率被邻居所传染.度中心性算法只计算了节点的邻居数目，却没有考虑邻居节点的属性.局部中心性算法（Local Centrality）［20］考虑了节点邻居的属性与间接邻居的属性，但不适用于有向网络.半局部算法（Cluster Rank）［21］是针对有向网络的关键节点识别算法，该算法考虑了节点邻居的属性与聚类系数在网络传播中的影响.半局部算法的准确性优于局部中心性算法与度中心性算法.

（2） 全局属性. 基于网络全局属性的关键节点识别算法考虑的是节点在整个网络中的属性.较为常用的算法有介数中心性算法（Betweenness Centrality）［21］和接近中心性算法（Closeness Centrality）［21］.在介数中心性算法中，判断节点的关键性指标是该节点在网络中进行信息传播时的负载量.具体的判别方法是计算出任意两个节点之间的最短路径，若一个节点包含的最短路径数越多，则该节点的关键程度越大.接近中心性算法表达节点到达网络其他节点的快慢程度.基于网络全局属性的关键节点挖掘算法准确性较高，但计算复杂度也很高.

（3） 位置属性. 基于网络位置属性的关键节点识别算法是根据节点在网络中所处的位置来度量该节点的关键程度.若一个节点在网络中处于核心位置，则认为其影响力较大.反之，则认为该节点的影响力有限.K-壳分解算法（ K-Shell）［22］是最经典的基于网络位置属性的关键节点挖掘算法. K-壳分解算法的实现方式是逐层去除小于等于度为K的节点，将节点归为不同的层次，处于网络内层的节点最为关键.基于网络位置属性的挖掘算法对网络结构有一定的要求.例如K-壳分解算法对星型网络和BA无标度网络不适用，并且难以确定各个指标的最佳权重因子.

（4） 随机游走. 基于随机游走的关键节点识别算法是一种动态识别关键节点的过程，主要应用领域是搜索引擎用来分析网页间质量的排序.该算法具体的实现方式是研究网页之间的关联指向，若一个网页被多个高质量网页所指，则证明其本身质量较高.常见的方法有HITS算法（Hypertext-Induced Topic Search）、谷歌搜索引擎使用的PageRank算法以及Leader Rank算法等［23］.

除了以上方法外，还有一些方法从其他角度出发，基于网络的连通程度、网络中边的属性等方面对节点的关键程度进行判断.这些方法都是从单一角度对节点进行度量，存在着表征不全、准确率低等问题.节点的关键性不仅由网络结构决定，还与节点自身特性以及邻居节点的信息有关.

3 基于GCN的关键节点识别技术

3.1 关键节点识别架构

基于GCN的关键节点识别方法流程如图1所示.

该方法主要分为4个步骤：数据处理、特征提取、生成关键节点识别模型、网络关键节点预测.首先，在数据处理过程中我们将一些网络数据中含有的极少量孤立的节点进行移除操作，使得本方法所使用的输入图例均为连通图;其次，进行特征提取.在网络中提取每个节点的二度子图，构建子图网络，提取子图网络的特征（详见第3.2节），并为每个节点构建7个特征组成的特征向量（详见第3.3节）.将每个节点的子图网络特征和特征向量作为模型的原始输入.为了避免实验过度拟合，在将特征送入模型进行学习前，对提取的特征进行归一化处理;接着，构建关键节点识别模型.根据提取到每个节点的特征输入到GCN层进行学习，同时为了更好地利用节点自身属性，该层增加了跳跃连接.然后通过三个全连接层对关键节点预测任务学习;最后，输入图例数据，通过回归损失函数MSE计算出最小损失，该模型的输出值是预测网络中每个节点的关键性得分情况.

3.2 构建子图网络

本文的研究对象是无权无向网络G，每个G由点集V={v1，v2，…，vn}和边集E={e1，e2，…，en}构成.在本文中N代表网络中存在节点的数量，E代表网络中存在边的数量.网络G的邻接矩阵为A=aijN×N，定义为

aij=1， 节点i和节点j存在连边0， 节点i和节点j不存在连边（1）

在GCN模型中，节点的特征与其邻居网络关联较大，节点的邻居网络对该点关键性起着至关重要的作用.每一层GCN的输入是邻接矩阵和节点的特征.根据三度影响力原则［24］，本文选取距离目标节点不超过3的邻居节点构建该点的二度子图网络，计算出子图网络的对称归一化拉普拉斯矩阵 （Symmetric Normalized Laplacian），其中节点的搜索方式为广度优先搜索（BFS）.

3.3 特征提取

根据现存关键节点识别方法的诸多不足，我们对此模型的特征有了以下三方面的考虑：（1） 对目前使用广泛的基于网络的局部属性、全局属性、位置属性等方法进行综合；（2） 增加了节点的圈比、桥接值、节点嵌入等三个更具判别能力的点的特征属性，用于弥补和完善其它方法存在的缺陷；（3）根据GCN的特点，抽取图例中节点的子图构建特征.

本文方法使用的7个特征具体如特征（1）～（7），这些特征对网络结构、节点信息以及邻居节点的信息进行汇总，从不同的角度深入剖析复杂网络.其中，特征（1）～（3）弥补和完善了现存方法的缺陷，特征（4）～（7）对使用广泛的基于网络结构的方法进行综合.

（1） 节点的圈比（Node Cycle Ratio）.节点的圈比指一个节点参与到其他节点的最短圈（包含这个节点的长度最小的圈）的程度.定义Si表示与节点i相关联的最短循环的集合，S=∪i∈VSi是G中所有最短圈的集合.定义圈数矩阵C=cijN×N刻画G的圈结构，N是节点数.如果i≠j，则cij是通过节点i和j的圈数.如果i=j，Cij是S中包含节点i的圈数.圈比ri估计了节点i参与S中其他节点的最短圈的重要性.

ri=0， cii=0∑j，cij>0cijcjj， cii>0（2）

在此定义中，仅考虑与每个节点相关的最短圈.在节点的圈比中节点是否重要取决于它对邻居节点的参与程度，圈上的邻居节点越多，节点本身的圈数越多，则该节点越重要.将节点的圈比作为特征对网络局部属性的缺陷做出了完善和补充.

（2） 节点的桥接值.复杂网络具有社团结构，符合社会学的“弱连接的强度”理论：1）弱连接（Weak Tie）各个社团之间联系稀疏；2）强连接（Strong Ties）社团内部节点联系紧密，使用社区发现法能将网络分为不同的社团.

本文采用Louvain社区发现算法对网络进行划分，模块度（Modularity）为衡量社团划分质量的标准.令C代表网络社团，Ci与Cj表示节点i与节点j在网络中的分属社团.若节点i与节点j同属一个社团，则δ的值为1，反之δ的值为0.令ev w为社团v和w之间的连边占整个网络中边的比例，则有以下公式：

ev w=12M∑ijaijδCi，vδCj，w（3）

av=12M∑idiδCi，v（4）

其中，αv是一边与社团v中节点相连的边在整个网络中的比例，di表示点i的度数.

模块度Q的表示公式是

Q=12M∑ij（aij-didj2M）∑vδCi，vδCj，v，

简化后表示为

Q=∑ev v-a2v（5）

桥接值VC描述节点连接的社团种类，即该节点的邻居节点所属的社团情况.VCi定义为与节点i直接相连的社团数量（包括自己所在的社团）.

例如，在图2网络中，可以将网络分为4个社团G1、G2、G3、G4.

其中，G1=v1，v2，v3，v4，v5，v6；G2=v11，v12，v13，v14；G3=v7，v8，v9，v10；G4=v15，v16，v17，v18，v19，v20，v21.节点1的桥接值为VC（1）=2，节点2的桥接值为VC（2）=1，节点11的桥接值为VC（11）=4.

节点桥接值越大，证明该节点参与社团越多，能够获得的信息种类越多.将节点的桥接值作为特征弥补了节点位置属性存在的缺陷.

（3） 节点嵌入.图的表示学习的特点是自动学习网络的特征，能够针对不同任务学习得到适合任务的嵌入表示.节点嵌入的学习方式为无监督学习.本文使用node2vec［25］进行编译用以保留网络的结构信息，将节点映射到嵌入空间，为节点做One-hot［26］编码，然后用One-hot编码乘以嵌入矩阵，得到每个节点的节点嵌入向量（Node Embedding Vector）.

（4） 度中心性.节点的度是网络局部属性中使用最广泛的一种方法，节点i的度ki为与该节点直接相连的邻居节点的数量.

ki=∑Nj=1aij=∑Nj=1aji（6）

节点的度属性因计算方便快捷、时间复杂度低等优点使之成为基于网络局部属性中最具有代表性的关键节点识别算法.它的适用范围很广，特别是在网络中边稠密、网络结构复杂的情况下，可以快速计算出网络中的大度节点.除此之外，在研究网络脆弱性问题中，保护网络中的大度节点对维护网络鲁棒性起着至关重要的作用.

（5） 介数中心性.节点的介数中心性是该节点在网络中进行信息传播时的负载量.计算出G中任意两个节点间的最短路径，若一个节点被最短路径包含的次数越多，则该节点i的负载量越大，该节点越重要.节点vi的介数定义为

BCi=∑i≠s，i≠t，s≠tgis tgs t（7）

其中，gs t代表点s到点t最短路径的数目；gis t代表点s到点t的最短路径里经过点i的数量.介数中心性考虑到了网络的整体结构属性，因其表示信息在网络中传播时的忙碌程度的特性，在研究网络通信问题中使用广泛.在网络中移除介数大的点可对信息传播造成巨大影响，介数中心性的时间复杂度较高，是基于网络全局属性中经典的关键节点识别算法.

（6） K-shell分解法.节点的K-shell值是对节点所处网络位置的评分.节点所处于的位置越贴近网络的内部，则该节点的影响力越大.相反，若节点处于网络的边界位置，则节点关键程度较小.实现方法是将网络中处于最边缘的节点逐层删去，留下的处于网络核心位置的节点作为关键节点.具体的过程如图4所示.

K-shell分解法时间复杂度低，适用于大型网络中关键节点的识别，是基于网络位置属性中常用的关键节点识别算法.

（7） 紧密中心性.节点的紧密中心性是用来描述节点到达其他节点的速度快慢，体现了节点在网络中的紧密性，表达节点i到达网络中其他节点的速度快慢.紧密中心性的计算公式如下.

CC（i）=n-1∑j≠idij（8）

di=1n-1∑j≠idij（9）

式中，dij是节点i和节点j之间的距离.可以看出，节点的紧密中心性越大，该节点距离其他节点越近，则该点处于网络的中心位置.在信息传播中，接近中心性可以很好地衡量信息的流动性.节点处于网络中心位置具有更好的传播能力，它的时间复杂度较高，是基于网络全局属性中常用的关键节点识别算法.

3.4 基于GCN的关键节点识别模型

GCN是针对图的特征提取器，其操作对象是图数据，能够对图的空间特征进行提取.利用这些特征可以实现图分类、链路预测以及图嵌入表示等功能.GCN可以分为两类：（1） 基于空间的GCN方法，它将图卷积核定义为来自邻居网络的特征信息，迭代地对邻居信息进行聚合，同时考虑了节点特征和子图特征;（2） 基于频谱的GCN方法，它主要涉及信号处理范围，通过引入滤波器来定义卷积核.

本文选取的是第一类基于空间的GCN方法.本文建立的复杂网络关键节点识别模型的GCN层定义如下.

Hi+1=σAHiWi+bi（10）

其中，A是二度子图网络的对称归一化拉普拉斯算子（Laplace Operator）；Hi表示第i个GCN层的节点；Wi和bi分别是可训练的权重和偏差参数；σ是非线性激活函数.我们将其设置为指数线性单元（Exponential Linear Unit，ELU）函数［27］.H0是输入层中邻居节点的特征向量.此外，为了更好地利用节点功能，我们在GCN层添加了Skip Connection［28］.同时，为了避免过度拟合，应用了基于退化学习率的Dropout技术.

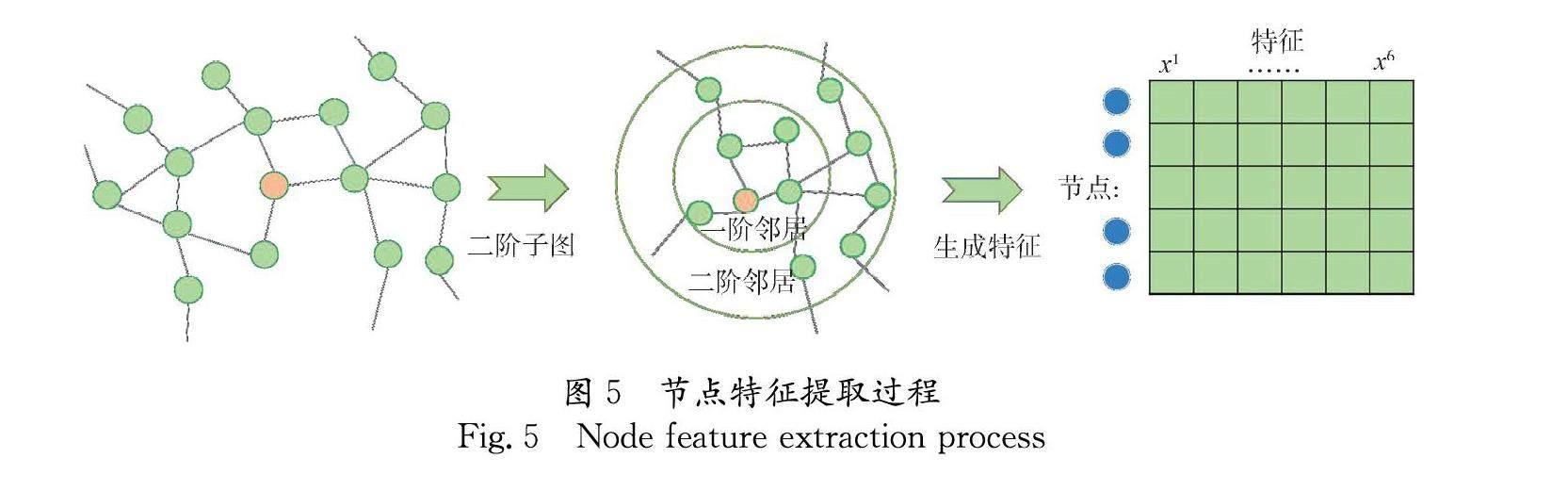
本方法中节点的特征提取过程如图5所示.首先，根据网络结构提取出节点i的二度子图;然后根据上文，分别提取出描述网络与节点相关信息的7个特征;最后，与子图特征一起拼接成特征向量，作为模型的输入.

为了加速实验拟合过程，本文使用最大最小标准化（Min-Max Normalization）方法对特征进行归一化处理，使每个特征值映射到［0，1］之间.

GCN层后是三个全连接层，起到分类作用.通过特征学习将网络中的节点进行统一评分，得分高的节点关键程度高，被分为关键节点.第一个全连接层后使用基于退化学习率的Dropout技术拟合数据集.为了避免出现过度拟合的现象，第二和第三个全连接层后使用了指数化线性单元ELU非饱和激活函数，用以缩短训练时间并提高准确度.模型的输出值是网络中每个节点的关键程度得分情况，本文选取得分前0.1N的节点为网络中的关键节点.

4 实验评估

4.1 实验数据

本文所用的实验数据均为公开数据集.这些数据是来自不同领域的真实网络，网络规模与网络类型多样化［27］.包括： （1） Zebra是一个动物网络;（2） Email是西班牙罗维拉维尔吉利大学的电子邮件通信网络;（3） C.elegans是秀丽隐杆线虫的神经网络;（4） NS-GC是从事NS42的科学家合作网络;（5） Erdos是一个科学合作网络，其中节点和链接代表个人和科学合作;（6） BA网络是无标度网络;（7） Air traffic control是美国航空运输网络;（8） Friendship是一个包含网站Hamsterster的用户之间友谊的网络.所有网络的详细参数如表1所示.

表1中，N表示的是网络的节点数目；E表示的是网络的连边数目；〈k〉表示网络的平均度〈k〉=1N∑Niki； 〈L〉表示平均路径长度；〈c〉表示网络的平均聚类系数.

〈c〉=1n∑ni=12IiΓiΓi-1′ （11）

其中，Ii表示节点i的直接邻居之间的边数.

本文采用流行病传播模型与牵制控制两种评估方式对实验结果进行评价.对比的五种算法有：节点度（D）、介数中心性算法（BC）、接近中心性算法（CC）、H-度中心性算法（H-index）和K-壳分解算法（K-shell）.

4.2 流行病传播实验

评价关键节点识别方法的准确性时，采用较为广泛的方法是基于传播动力学中的SIR传播实验.在SIR仿真实验中，网络中的节点具有三个状态，分别是易染态S（能够被处于感染态的邻节点感染）、感染态I（感染态的节点在固定时间后会变为免疫态）以及免疫态R（免疫态的节点稳定，不会被其他状态感染）.其中处于易染态S的节点会在每个时间步长t内以概率β被处于感染态I的节点所感染，也变为感染态I.随后，处于感染态I的节点会以固定速率γ变为免疫态R.SIR模型从传播速度与传播范围两方面对节点关键程度进行考察.本文选择排序索引中的前0.1N个节点作为初始感染源，时间步长为t，对其他节点进行感染.按某一时间步t的累计感染节点数量作为最终的传播范围，通过比较t时刻累计感染节点数量来衡量初始感染源的重要程度.被感染的节点越多，表明选取的初始感染源节点的传播能力越强，关键程度越大.

本文选取扩散阈值β = βc和γ=1对每个网络进行SIR实验，感染源为每种关键节点识别方法排序索引的前0.1N个节点.

βc=〈k〉〈k2〉-〈k〉（12）

其中，〈k〉是网络的平均度数；〈k2〉是平均平方度数.

图6是在时间步长t=1，t=2，…，t=10、扩散阈值β=βc、 γ=1的情况下，五类关键节点识别方法与本方法感染的关键节点数量.横坐标为时间步长t，纵坐标为感染的节点数量，由于实验存在随机性，以下为500次独立运行SIR模型的结果.

由图6可以看出，在8个网络中，将本文方法求得的节点作为感染源在SIR模型中的感染规模均大于其他5种关键节点识别方法.特别是在Friendship网络中，在扩散阈值β取0.08的条件下，使用本方法时每个时间步长t时的感染规模都远远高于其他五种方法.在t=10时网络趋于稳定状态，使用本文方法网络的平均感染规模为727.95，另外五种对比方法中最大平均感染规模为470.48.在NS-GC网络和C.elegans网络以及Air traffic-control网络中，本文方法在每一个时间步长t时的感染规模都高于其他方法;在Email网络中，虽然前5个时间步长内本文方法略低于K-shell方法，但是当SIR仿真模型在网络中感染的节点最终达到平衡时，本文方法的感染规模为323.03，K-Shell方法的平均感染规模为312.42，低于本文中的方法.

图7是进行SIR仿真实验中部分网络在每个时间步长t时网络的感染详情.横坐标为时间步长t，纵坐标为几类关键节点识别方法，颜色越深代表感染节点数越多，识别出的关键节点越准确.

由图7可以看出，在SIR模型中本文方法的感染速率与感染规模均明显优于其他方法.综上所述，在传播动力学SIR模型中，本文方法识别出的关键节点在传播速度与传播范围两个方面均高于其他方法.使用本文提出的基于GCN的关键节点识别方法比传统方法更具有优势.

4.3 牵制控制实验

现实中网络规模庞大且结构复杂，因此想要实现对网络的完全控制需要耗费大量成本.在现实场景中，为了节约控制网络过程中使用的资源成本，通常会对网络中的少量节点施加控制使目标网络在有限时间达到相应状态，这个过程被称为网络的牵制控制.在牵制控制实验中，根据节点索引逐个固定节点，并量化网络的可同步性.通过测量在同步过程中控制节点所产生的影响来评估节点的关键程度.

复杂网络G由N个节点构成，它们之间相互作用的动力学公式为

x˙i=fxi+σ∑Nj=1lijΓxj+Uixi，…，xN（13）

其中，向量xi∈Rn是节点i的状态；函数f（·）描述节点的自动力学；正常数σ表示耦合强度；内耦合矩阵Γ：Rn→Rn是半正定的；Ui（xi，…，xN）是施加在节点i上的控制器.网络G的拉普拉斯矩阵的定义如下：L=lijN×N，如果（i，j）∈E，则lij=-1；如果（i，j）E and i≠j，则lij=0；如果i=j，则lii=-∑j≠1lij.

假设网络在时间为t时的目标状态s（t）满足：s˙（t）=f（s（t）），s（0）=s0，牵制控制实验的目的就是通过控制网络中的部分节点使网络状态趋近于目标状态s（t）.此时网络的真实状态与目标状态中存在的误差为：ei=xi（t）-s（t）.

若对网络中前l个节点施加控制，控制器Ui（xi，…，xN）的定义如下式.

Ui=-diΓei，di=hieTiΓei，1≤i≤lUi=0，l+1≤i≤N（14）

其中，hi是一个任意的正常数.

在这里，提出了一个度量P，名为牵制效率，以表征受牵制控制的索引的性能.

P=1Qmax∑QmaxQ=11μ1L-Q（15）

其中，Qmax表示固定节点的最大数量；L-Q是主子矩阵，通过从原始拉普拉斯矩阵L中删除对应于Q个固定节点的Q个行和列而获得；μ1L-Q是L-Q的最小非零特征值.

P随着固定节点数量的增加而衰减.P值越小，衰减越快.更快的衰减对应于更好的性能.本文将Qmax设置为每种关键节点识别方法排序索引的前0.05N～0.1N个节点.

表2和表3是数据集中的5个网络在Qmax设置为0.05N和0.1N两种情况下，不同方法下的牵制效率P.其中加粗数据为表现最佳的牵制效率.

由表2和表3可知，选取前0.05N个节点与前0.1N个节点的实验结果相似，本文方法总体占据优势.从牵制效率P的性能考虑，在36组实验中本方法有34次表现为最佳的牵制效率.剩余2次实验为Email网络的实验，本方法的性能略低于K-Shell方法，排名第二.但是与BC、D、H-index、CC等四类方法的结果相比明显具备更快的衰减率和更高的性能.综上所述，本方法识别出的节点对网络控制产生的影响更大，节点关键程度更高.

5 结 论

复杂网络中关键节点识别研究取得了一定进展，但仍存在着方法适用范围局限、识别准确率低等缺陷.本研究根据上述缺陷提出了基于GCN的复杂网络关键节点识别方法，优势如下：（1） 考虑全面.使用深度学习的方法对网络结构、节点属性、邻居节点间结构进行融合分析. （2） 算法适用范围广.在不同类型的真实网络中实验结果良好.（3） 识别准确率高. SIR实验证明本方法确定的关键节点在复杂网络中的传播速度与传播范围两方面均优于其它方法;牵制控制实验证明本方法确定的关键节点对网络控制产生的影响更大.综上所述，本研究提出的方法与其他方法相比更具优势.

参考文献：

［1］ Ju Y， Zhang S， Ding N， et al. Complex network clustering by a multi-objective evolutionary algorithm based on decomposition and membrane structure ［J］. Sci Rep： UK， 2016， 6： 1.

［2］ 韩忠明， 吴杨， 谭旭升， 等. 面向结构洞的复杂网络关键节点排序［J］. 物理学报， 2015， 64： 058902.

［3］ Malliaros F D， Rossi M E G， Vazirgiannis M. Locating influential nodes in complex networks ［J］.Sci Rep： UK， 2016， 6： 19307.

［4］ De Domenico M， Solé-Ribalta A， Omodei E， et al. Ranking in interconnected multilayer networks reveals versatile nodes ［J］. Nat Commun， 2015， 6： 1.

［5］ 任晓龙， 吕琳媛. 网络重要节点排序方法综述［J］. 科学通报， 2014， 59： 1175.

［6］ 韩忠明， 陈炎， 李梦琪， 等. 一种有效的基于三角结构的复杂网络节点影响力度量模型［J］. 物理学报， 2016， 65： 168901.

［7］ Bellingeri M， Bevacqua D， Scotognella F， et al. A comparative analysis of link removal strategies in real complex weighted networks［J］. Sci Rep： Uk， 2020， 10： 1.

［8］ Zhu C， Wang X， Zhu L. A novel method of evaluating key nodes in complex networks ［J］. Chaos Soliton Fract， 2017， 96： 43.

［9］ 朱军芳， 陈端兵， 周涛， 等. 网络科学中相对重要节点挖掘方法综述［J］. 电子科技大学学报， 2019， 48： 595.

［10］ Lü L， Chen D， Ren X L， et al. Vital nodes identification in complex networks［J］. Phys Rep， 2016， 650： 1.

［11］ Chiang W L， Liu X， Si S， et al. Cluster-gcn： An efficient algorithm for training deep and large graph convolutional networks［C］//Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Alaska：ACM， 2019： 257-266.

［12］ Fan T， Lü L， Shi D， et al. Characterizing cycle structure in complex networks［J］. Commun Phys： UK， 2021， 4： 1.

［13］ 赵之滢， 于海， 朱志良， 等. 基于网络社团结构的节点传播影响力分析［J］. 计算机学报， 2014， 37： 753.

［14］ 梁世娇， 柴争义. 基于多目标自适应Memetic算法的复杂网络社区检测［J］. 江苏大学学报： 自然科学版， 2020， 41： 262.

［15］ 张淼，梁延研，黄相杰.基于集成学习的复杂网络链路预测及其形成机制分析［J］.重庆邮电大学学报： 自然科学版， 2020， 32： 759.

［16］ Cavallari S， Zheng V W， Cai H， et al. Learning community embedding with community detection and node embedding on graphs［C］// Proceedings of the 2017 ACM on Conference on Information and Knowledge Management. Singapore. ［S.l.］： ACM， 2017： 377.

［17］ 潘侃， 尹春林， 王磊， 等. 基于特征工程的重要节点挖掘方法［J］. 电子科技大学学报， 2021， 50： 930.

［18］ Zhong L， Gao C， Zhang Z， et al. Identifying influential nodes in complex networks： A multiple attributes fusion method［C］// Proceedings of the Inte-rnational conference on active media technology. Warsaw， Polan： Springer， 2014： 11.

［19］ Kang W， Tang G， Sun Y， et al. Identifying influential nodes in complex network based on weighted semi-local centrality［C］// Proceedings of the 2016 2nd IEEE International Conference on Computer and Communications （ICCC）. Chengdu： IEEE， 2016： 2467.

［20］ Samadi N， Bouyer A. Identifying influential spreaders based on edge ratio and neighborhood diversity measures in complex networks［J］. Comb Probab Comput， 2019， 101： 1147.

［21］ Vernize G， Guedes A L P， Albini L C P. Malicious nodes identification for complex network based on local views ［J］. Comput J， 2015， 58： 2476.

［22］ 喻依， 甘若迅， 樊锁海， 等. 基于 PageRank 算法和 HITS 算法的期刊评价研究［J］. 计算机科学， 2014（Z6）： 110.

［23］ 王名扬， 贾冲冲， 杨东辉. 基于三度影响力的社交好友推荐机制［J］. 计算机应用， 2015， 35： 1984.

［24］ Ribeiro L F R， Saverese P H P， Figueiredo D R. struc2vec： learning node representations from structural identity［C］//Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2017： 385.

［25］ Buckman J， Roy A， Raffel C， et al. Thermometer encoding： One hot way to resist adversarial examples ［C］//International Conference on Learning Representations. Vancouver： ICLR， 2018.

［26］ Clevert D A， Unterthiner T， Hochreiter S. Fast and accurate deep network learning by expon-ential linear units （elus）［ EB/OL］.（2015-11-23）［2022-08-22］.https：//doi.org/10.48550/arXiv.1511.07289.

［27］ Bae W， Yoo J， Chul Y J. Beyond deep residual learning for image restoration： Persistent homology-guided manifold simplification ［C］// Proceedings of the IEEE Conference on Computer Vision and Pattern recognition Workshops. Honolulu： CVPRW， 2017.

［28］ Rossi R， Ahmed N. The network data repository with interactive graph analytics and visualization［C］//Twenty-ninth AAAIConferen-ce on Artificial Intelligence.Austin： AAAI Press， 2014： 753.

引用本文格式：

中 文： 杨洋， 王俊峰. 基于GCN的复杂网络关键节点识别研究［J］. 四川大学学报： 自然科学版， 2023， 60： 032002.

英 文：  Yang Y， Wang J F. Research on key node identification of complex network based on GCN ［J］. J Sichuan Univ： Nat Sci Ed， 2023， 60： 032002.