复杂环境下多传感器信息融合的无人驾驶汽车智能悬架自动控制方法

丁鹏 邹晔 郭祥龙 陈珣 鲁福硕

关键词：无人驾驶汽车；半主动悬架；多传感器信息；信息融合

型障碍物路面（如碎石、凹坑、减速带）时，会影响悬架的减振效果，甚至在没有驾驶员（或系统）干预车速的情况下，严重影响汽车行驶的平顺性和安全性[1-2]，因此需对无人驾驶汽车悬架阻尼和车速根据路面状况提前控制。目前对无人驾驶汽车的研究多集中在驾驶行为的决策与路径规划，重点发掘人类驾驶员认为具有挑战性或缺乏操纵能力的复杂动态场景下的潜力[3-7]，普遍忽略了悬架控制对智能汽车安全性能的影响。

悬架控制方法有多种，文献[8]采用卷积分神经网络方法识别路面等级，并应用于半主动悬架控制策略中。文献[9]提出反馈线性化Kalman观测器控制磁流变悬架，设计了非线性磁流变悬架系统系统。文献[10]提出阻尼连续可调的抗俯仰液压互联悬架系统。陈龙等设计了阻尼可切换的半主动悬架，通过仿真方法获取各阻尼模式的减振系数，改善了汽车的平顺性[11]。孙晋伟等研究了多目标布谷鸟优化和路面识别算法，提出非线性悬架系统自适应控制方法[12]。AbTalib等提出萤火虫算法（fireflyalgorithm，FA）的智能优化器，结合比例积分微分控制器对半主动悬架进行控制[13]。文献[14]提出模糊保证成本H∞控制器（fuzzyguaranteedcostH∞control，FGCHC），以确保所控的闭环车辆主动悬架系统渐近稳定。文献[15]设计了加速度驱动刚度模糊控制策略（acceleration-driven-stiffnessfuzzycontrolstrategy，ADSFC）和基于Skyhook的控制策略，控制空气弹簧内压和磁流变阻尼器电流，实现刚度和阻尼的调节。上述悬架控制方法在一定程度上改善了汽车的平顺性，但是鲜有涉及无人驾驶车辆在随机性小型障碍物或破损路面时，对悬架平顺性和安全性的控制。

无人驾驶汽车悬架控制基础是路面识别，现有研究对路面识别集中在两类，一类是基于激光、雷达等检测手段的路面纹理和裂缝的识别，主要应用于破损道路的质量监控[16-19]；另一类是基于视觉图像处理技术的路面不平度检测与识别，主要应用于道路等级的识别[20-24]。上述路面检测方法不能有效计算路面小型障碍物或破损路面的长宽高等详细信息。另外，由于汽车行驶受恶劣天气影响，现有检测方法不能满足汽车实时对路面状况的提取，最终影响阻尼输出质量。无人驾驶汽车凭借多传感信息融合技术能够提高路面不平度的检测精度，在此基础上对悬架和车速提前预控制，以满足行驶的平顺性与安全性。

本文提出一种多传感器信息融合的无人驾驶汽车智能悬架控制方法。利用摄像头和雷达波扫描并识别不平路面状况，并创建基于摄像头和雷达波采集信息的路面不平度数学模型，通过检测边缘交并比和GNN算法对不平路面进行信息融合和匹配，得到复杂环境下可信度较高的路面不平数学模型;结合悬架振动模型，构建路面不平数学模型与汽车预振动量之间的关系;提出利用车速和路面不平信息的方法计算半主动悬架最佳阻尼比，并将悬架调节至该阻尼比，以使悬架提前适应不同路面状况，提高汽车平顺性。

1悬架模型

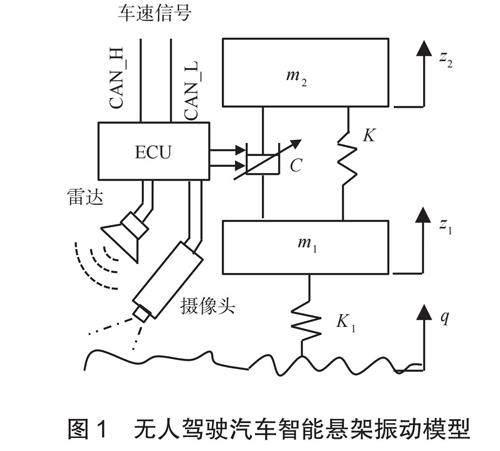
为了从理论上对提出的方法进行可行性判断，同时为悬架模块（electroniccontrolunit，ECU）调节阻尼提供控制参数，需要建立基于多传感器信息融合车辆1/4悬架模型，以揭示路面不平度与汽车预振动量之间的关系，模型图1所示。

图1中m1为悬架非支撑质量（簧下质量）；m2为悬架支撑质量（簧上质量）；K为减震器弹簧刚度；C为减震器阻尼可变系数；K1为轮胎的刚度；q为输入的路面不平度函数；z1为轮胎的垂直方向位移；z2为车身的垂直方向位移；根据牛顿第二定律，结合图1悬架模型的受力关系，建立悬架二自由度微分振动方程：

由式（8）―（11）可知，已知路面不平度输入，可求出对应的车身与车轮的振动量。假设预先检测到路面不平度输入数值，则可预测车身振动量，多传感器信息融合技术能够提前够精准的检测车辆前方的路面状况，输入悬架ECU并计算车身预振动量，根据此预振动量提前控制半主动悬架的阻尼，使车辆悬架阻尼提前适应路面振动输入。路面状况的感知和输入是该系统的基础和关键环节之一。

2多传感器融合的路面不平度识别

汽车行驶路面状况和环境条件复杂多变，单一传感器检测的路面信息具有一定程度的不确定性和不可靠性，这种可信度不高的病态数据结构会对悬架阻尼造成错误的控制，导致汽车平顺性、操纵性和安全性变差。多传感器信息融合技术是将不同类型的传感器在相同的时间内对同一路面信息进行数据采集，悬架控制器对不同传感器取得路面图像和序列信息进行融合和综合决策，形成新的路面信息阐述。

2.1基于图形视觉的路面不平度检测

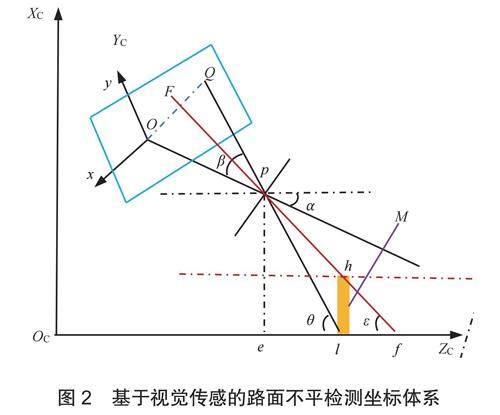
路面不平度也称路面平整度（roadsurfaceroughness），指道面表面相对于理想平面的竖向偏差[25]。运用可见光电荷耦合元件（charge-coupleddevice，CCD）图像传感器扫描具有一定不平度的路面状况，该类型传感器具有较高的几何纹理信息、时空分辨率以及丰富的外观和颜色信息。基于此，运用典型的基于图像灰度阈值的分割方法识别并规划不平路面区域边缘[26]，将图像灰度值大于閾值的像素归为图像目标（不平路面），反之将像灰度值小于阈值的像素归为图像背景（正常路面）。建立路面物理坐标系和图像坐标系的对应关系，以路面小型障碍物（落石、砖块、减速带等）为例构建路面不平度计算方法，将三维物理场景投影到摄像机二维平面，图2中物理场景用三维场景坐标系Xc，Yc，Zc轴表示，投射到摄像机的二维平面用x、y轴表示，O点为图像坐标系的原点。

图2中p点为车载摄像头的安装位置，p点到O点之间的直线为摄像机光轴，两者之间的距离即为摄像机焦距，用Lop表示。假设摄像头在地面的垂直投影为e点，则p点到e点之间的距离，为摄像头到地面之间的距离，用Lpe表示。M为遗落路面上的小型障碍物，运用基于图像灰度阈值的分割方法识别并规划障碍物区域边缘，依据最大类间方差法选取像素最佳阈值，将路面图像中扫描的图像像素灰度值与该阈值相比较，小于该阈值的像素判定为正常路面，反之则为障碍物区域，由此即可得到不平区域边缘图像点的集合。障碍物边缘任一点为l，l点在图像坐标系的投影点记为Q，l点e点之间的距离则为摄像头到障碍物之间的距离，记为Lqe。设镜头安装俯仰角为α，l点的投影直线与路面（YCOCZC平面）之间的夹角为θ，该投影直线与光轴之间的夹角记为β。f点为障碍物上方任一点在地面上的投影，该投影直线与地面之间的夹角用ε表示。

根据坐标系（像素坐标系、图像坐标系、相机坐标系和世界坐标系）之间的关系，已知路面障碍物边缘投影点的像素坐标，可推出其在图像坐标系中的图像坐标，即Q点坐标。根据像素值，即可得出O点到Q点之间的距离LOQ。又因摄像机的焦距Lop可通过标定求出，根据图2中的几何关系（tgβ=LOQ/Lop），可求出β角。

根据式（12）可求障碍物边缘点集合到摄像机之间的距离Lpe，进一步判断障碍物边缘及长宽信息。同理可求出ε角数值、F点像素与图像坐标，由此推导障碍物高度集合信息。至此通过摄像头可以完整获得障碍物的边缘及高度信息等情况以及障碍物到摄像头之间的距离。

2.2雷达波检测路面不平度

毫米波雷达具有抗干扰能力较强、穿透能力优异，探测分辨较高的特点，适用于全天候路面状况的检测，是机器视觉传感与检测路面的有效补充。以破损路面凹坑为例，说明雷达波检测路面的方法如图3。

雷达在发射多束波检测路面过程中，图3中部分波（虚线表示）在凹坑底部发生偏转，偏离了原来的回波路线成为废波，其为有效波（实线表示），照射在路面反射之后返回雷达。假设雷达射出的n束波，根据缺失的废波和接收的有效波可以提取破损路面的轮廓和形状信息。定义照射在破损路面边缘区域的任意两条射线之间的距离为d，其中一条射线与地面的夹角为ψ，它可通过雷达接收到的回波信号间的相位差确定，深度为h，则通过缺失的废波可以测量和计算d的数值，则根据图3中的照射关系可得：

其中：Δτ为雷达的扫描角度误差，η为测量误差，破损路面凹坑的宽度为w。由于废波的存在，深度h仅能得到最小值，根据测量的最小值集合，可计算其数值。根据以上分析与计算即可构建雷达波检测到的路面信息。

2.3传感器信息融合策略

采用检测边缘框交并比的融合策略，假设视觉传感器与雷达波传感器对某一不平路面区域检测的边框分别为Kcam与krad，2个边框重合（交集）区域的面积为Sj，而2边框总面积（并集）区域为Sh，定义IOU交并比，即：

根据相关文献[27]可知，当式（14）中IOU的数值在0.6～1之间，可判断摄像机和雷达波均检测出目标路面，其测量结果相互认证和匹配，可信度较高。

对匹配不成功的数值，则用全局最近邻（graphneuralnetworks，GNN）算法进行数据关联[28]，设雷达和摄像头匹配不成功的目标点分别为m、n，它们到指定点（原点）的距离分别dr、dc，将所目标点到原点的距离按照数值大小进行排序，可得到视觉和雷达的目标点矩阵R，K，将雷达监测点作为已知点，摄像头检测点作为测量点。设vij（k）为k时刻雷达检测点和摄像头检测点的残差，它可使用式（15）表达为

其中：Sij-1（k）表示vij（k）的协方差矩阵，设Gi表示雷达检测点i的门限值，当归一化距离小于等于门限值时，表示摄像头检测点位于雷达检测点范围内，可以相互匹配。每个雷达检测点最多匹配一个摄像头检测点，反之亦然。计算GNN算法中的代价函数式为

通过计算代价函数，可完成剩余不平路面区域目标点的对接与匹配，实现雷达和摄像头传感信息的有效融合。

3多信息融合下悬架控制方法

在设计无人驾驶悬架自动控制策略中，既要满足悬架振动的舒适性指标，又要考虑突发性障碍物对悬架和车辆安全性能的影响。通过建立最佳阻尼比数学模型，分析无人驾驶汽车半主动悬架舒适性和安全性控制方法。根据悬架振动理论和相关文献研究[29-30]可知悬架的舒适性与安全性最佳阻尼比为其中：ζcom为舒适性最佳阻尼比，γ为刚度比，φ为质量比。

由式（18）和式（19）可知，悬架舒适性最佳阻尼比与安全性最佳阻尼比之间相互影响和制约，为了兼顾车辆安全与舒适性要求，需要对两者进行权衡与匹配，匹配之后的阻尼比称为综合性最佳阻尼比为ζopt，其取值方法为：当ζopt≤ζcom，取ζopt=ζcom；当ζopt≥ζcsec，取ζopt=ζcse；当ζcom<ζopt<ζsec，最佳阻尼比控制曲线如图4所示。

图4为路面不平输入、车速以及最佳阻尼比之间的控制曲面图。图中路面不平输入为多传感器采集并融合后输出的路面障碍物高度信息及凹坑深度信息，正值表示障碍物高度，负值表示凹坑深度。在路面输入良好的路面，即图4路面输入为0时，最佳阻尼比0.12为舒适性的最佳阻尼比，即在良好的路面上为保证乘员舒适性，悬架阻尼调整为最舒适性阻尼。分析图4还知，在同一路面，最佳阻尼比随车速的升高而增大，直到升至最大安全性最佳阻尼比0.42。正负路面（障碍物或凹坑距离地面距离）的数值越大，最佳阻尼比调整的数值愈大，這是出于汽车安全性考虑，防止汽车发生跳动。

半主动悬架采用电液连续阻尼控制减振器（continuousdampingcontrol，CDC），CDC通过电机控制杆旋转一定的角度，改变内外腔室节流孔流通面积，实现阻尼值的无级变化。控制器首先由路面状况和车速信号确定悬架最佳阻尼比，并以电压信号的形式输出作为基本控制电压；基本电压与反馈控制器输入的电压相比较（相减）取得偏差电压信号，偏差信号通过放大后控制电机转角，随后驱动减速齿轮副转动，带动控制杆旋转，从而调节减振器节流孔流通面积。转轴旋转的同时驱动一个滑动变阻器，传感该轴转角，作为系统的实时反馈信号，系统控制原理图如图5所示。

图5中最佳阻尼比控制信号为v0（s），G1（s）为放大器传递函数，G2（s）为电机传递函数，G3（s）为机械传动传递函数，G4（s）为反馈系统的传递函数。根据图5，可求出系统的闭环传递函数为其中，τ=JLa+KmKb为电机等效时间常数。

了定性分析系统机械传动过程，简化控制过程，设传动系统刚性为无穷大的理想状态，且齿轮副无传动间隙，机械传动传递函数为其中：N1、N2分别为输入和输出齿轮的齿数。

4悬架试验

对装有半主动悬架的无人驾驶汽车开展垂向典型工况下整车路面试验。样车为自制无人驾驶电动车，样车参数：悬架非支撑质量，即簧下质量m1为42kg；悬架支撑质量，即簧上质量为254kg；悬架的弹簧刚度m2为18kN/m；轮胎的刚度K1为2261kN/m。

图6为装有多传感器控制的悬架试验样车，毫米波雷达和标注摄像头用于车辆半主动悬架的控制，而激光雷达和其他摄像头则用于识别行人、车辆以及道路标志线，在这里不再赘述。

为了验证多传感器数据融合的有效性，分别在车辆前方5、10、20m的距离放置小型障碍物，其尺寸为长178mm、高35mm、宽45mm，分别记录雷达、摄像头及融合后的测量数据，结果如表1。

从表1的试验数据可得在5m范围内摄像头和毫米波雷达的测量数据准确率均在99%以上，此时摄像头测量准确率要高于毫米波雷达。在数据融合时，需考虑目标障碍物与车辆之间的距离，当近距离时，需增加摄像头测量数据的权重，多传感器融合后的数据的准确率可达99.5%以上，其最大误差较雷達和摄像头准确率分别提高4.6%、2.3%。随着距离的增加，在10m距离时摄像头和毫米波雷达的准确率均降低，多传感器融合数据准确率也随之降低，但与单个传感器相比准确度有所提升，融合后准确率仍可提升至99%以上，最大误差较雷达和摄像头准确率分别提高了4.4%、4.6%。在20m距离时，毫米波雷达的准确率要高于摄像头，数据融合时，需增加毫米波雷达测量数据的权重，分析表1可知，此时数据测量的准确率可达97.9%，最大误差较雷达和摄像头准确率分别提高了5.4%、5.6%，说明多传感器数据融合策略能够提高路面状况识别的准确性。

为了最大程度地展示多传感器信息融合控制的半主动悬架控制效果，在试验过程中选取单凸块试验，试验符合国标GB/T4970-2009要求。将单凸块置放于试验道路中间，按照车辆轮距调整两个单凸块之间的距离。试验道路平直，且路面干燥，不平度均匀无突变。汽车以均匀的速度驶过单凸块试验路段，测量并记录车辆加速度时间历程。分别记录装有被动悬架、常规的基于加速度控制式半主动悬架（传统半主动悬架）以及多传感器信息融合的智能悬架的样车通过试验路段产生的车身振动加速度信号，试验结果如图7—图10。

需要说明的是：被动悬架几何机构与参数确定之后，其刚度和阻尼都是不可调的，它只能保证在特定的情况下达到最优减振效果，难以适应不同的道路和使用状况；一般被动悬架的阻尼比设定范围为0.2～0.4。

传统半主动悬架指通过传感器感知路面状况和车身姿态，对阻尼参数进行调节，从而改善汽车行驶平顺性和稳定性的一种可控式悬架系统。传统半主动悬架主要采用加速度传感器采集车辆行驶过程中的振动状态，控制器根据加速度传感器反馈的振动量调节悬架阻尼，即“先振后调”。由于调控时滞的存在，可能会导致反馈控制系统的失稳，出现对安全极为不利的轮跳，严重影响了半主动悬架对车辆平顺性的改善，特别对短距离恶劣路况和不规则越野路面完全不起作用，其阻尼比调整范围为0.175～0.414。

与传统半悬架“先振后调”的控制模式不同，无人驾驶车辆悬架控制方式为“先调后振”。首先利用摄像头和雷达波扫描并识别不平路面状况，得到复杂环境下可信度较高的路面不平数学模型。提出利用车速和路面不平信息计算半主动悬架最佳阻尼比，并将悬架调节至该阻尼比（0.12～0.42），以使悬架提前适应不同路面状况，提高汽车舒适性。

试验车辆以30km/h速度驶过放置有单凸块的B级路面，分别记录被动悬架、基于加速度控制的传统半主动悬架以及多信息融合下控制的半主动悬架的车身加速度时域响应信号，如图7所示。图7被动悬架通过单凸块，车身垂直加速（verticalacceleration）最大峰值为7.8m/s2，且有多个余波峰值出现，随后波形逐渐趋于平稳，说明被动悬架减振效果弱。传统半主动悬架车身加速度最大值为7.6m/s2，随后出现的振动余波峰值迅速衰减，说明传统半主动悬架能够迅速衰减振动，但由于传统半主动悬架是基于振动加速度调控，即先振后调，所以会有一个较大的初始峰值出现。智能悬架架最大振动峰值为3.4m/s2，随后经历几个较小峰值的余波而趋于稳定，说明悬架系统检测到单凸块的存在，电脑模块根据单凸块的信息对悬架阻比进行了提前干预，悬架系统提前适应该路面状况，其最大振动加速度峰值与传统悬架振动加速度最大值减少43%。图8中0～30Hz频率区间功率谱响应情况，在20Hz频率附近形成共振，但对人体振动敏感区域4～8Hz范围内，功率谱增益值较小，说明改善效果显著。

图9中智能悬架动行程（suspensionworkingspace，SWS）的均方根值与被动悬架和传统半主动悬架分别下降了11.8%和8.6%，且最大值并未超出限位值，在驶过偶发性的落石等路面能够有效避免撞击。分析图10中轮胎的动变形（tiredynamictravel，TDT），发现智能悬架轮胎动变形，其均方根值相对于被动悬架和传统半主动悬架分别下降12.7%和5.9%，说明智能悬架能够增加车辆的附着能力，提高汽车的操纵性和安全性。

了进一步评估智能悬架悬架的控制效果，开展随机路面条件下时域和频率振动试验。车辆以60km/h速度匀速通过B级路面，记录车身振动加速度数值，并对比智能悬架、被动悬架和传统半主动悬架的试验结果，如图11和图12。

分析图11，在给定的试验条件下，装有被动悬架车辆车身振动速度峰达到3.72m/s2，传统半主动悬架车身振动加速度峰值为3.46m/s2，多传感器智能悬架车震振动加速度最大值为3.21m/s2，振动加速度有一定减少，与单凸块路面试验相比，振动改善减少，说明该类系统在破损路面、偶发性路障等条件下更能有效改善悬架平顺性。

图12为加速度频域响应曲线，由经典振动理论可知频率在4.0～12.5Hz区间内振动对人体的影响最大，对比图12中该段频率内，智能悬架幅值比与被动悬架和传统半主动悬架相比，功率谱增益值明显较小，说明改善效果显著。通过分析上述数据可知智能悬架在结构化路面能够有效减少车身振动量，提高汽车行驶的平顺性和舒适性。

5结论

在建立汽车悬架振动模型的基础上，研究了复杂环境下多传感器信息融合的无人驾驶汽车半主动悬架自动控制方法，开展了垂向典型工况下整车路面试验，取得了以下结论：

1）基于多传感器信息融合控制的无人驾驶汽车，能够在复杂的环境下，利用摄像头和毫米波雷达识别正常路面的不平区域，特别对路面随机出现的凸块、凹坑以及减速带有较高的辨识度。车辆根据提前检测的路面信息和车速对悬架阻尼进行预调节，可有效提高汽车行驶的平顺性和安全性。

2）建立了基于单目视觉和毫米波雷达检测路面模型，利用GNN算法对两类型路面模型进行融合，使车辆在复杂环境下测量的结果相互认证和匹配，得到了可信度较高的适用于悬架控制的路面不平数学模型。

3）分析了不同悬架在典型工况下的振动试验，特定条件下，多传感器信息融合控制的半主动悬架振动峰值减少了43%以上，验证了数学模型的正确性，为分析无人驾驶汽车悬架控制提供了理论基础和创新方法，对无人驾驶汽车的研制和设计具有一定的工程价值。