重型载货汽车长下坡制动工况辨识
2023-04-29史培龙高艺鹏张子豪赵轩余强
史培龙 高艺鹏 张子豪 赵轩 余强

关键词:汽车工程;重型载货汽车;制动工况;Markov-MonteCarlo方法;工况辨识;滚动时间窗
传统持续制动系统的开启和关闭主要依靠驾驶人的主观判断和操作,由于疲劳驾驶或路况不熟悉等因素影响,重型载货汽车在下坡行驶过程中过度依赖行车制动系统而引起整车热衰退问题,因此有效识别车辆的行驶状态为车辆控制提供决策依据对于提高行驶安全性有重要意义。车辆的行驶工况能够表征特定车辆在某种交通环境中的运行状态[1],但是传统的汽车行驶工况用于新能源汽车的能量管理,未考虑山区公路车辆行驶特性。为了实现持续制动系统主动控制,有必要开展重型载货汽车长下坡制动工况构建及辨识方法研究,为持续制动系统介入或退出决策提供依据。
关于行驶工况的构建,国内外相关学者做了不少研究,并取得了一定成果。为了反映车辆在真实道路下行驶状态,速度、加速度[2-3]通常作为重要参数用于构建工况,一些学者[2]考虑了交通流带来的影响,选择城市、环路、乡村、高速路段等不同等级的道路建立循环工况;一些学者考虑到城市地理特征因素,建立了典型城市(如西安[3]、呼和浩特[4]、大连[5]等)循环工况。但是,建立工况目的均用于混合动力汽车或纯电动汽车的能量管理,车型多针对乘用车或城市客车。通过片段划分[6]、主成分分析等数据处理后,运用Markov-MonteCarlo[7]、Multi-dimensionalMarkov链[8]、多岛遗传算法(multi-islandgeneticalgorithm)[9]、两阶段聚类等方法建立相应工况。上述参数及方法构建的工况未含道路坡度信息和制动踏板动作特性数据,不能够准确反映山区道路车辆行驶状态特征。
工况辨识方面,目前有遗传混合整数优化算法[10]、模拟退火算法[11]、PSO-SVM算法[12]等用于工况辨识,但是用于构建工况的数据未考虑山区公路车辆行驶特性。余强等[13]提出了几种制动方式联合制动的智能控制方案,但是未对持续制动系统介入和退出方法展开研究;韩云武等[14-15]提出了辅助制动系统平滑进入与退出的控制策略,但是仅针对新能源汽车;利用坡度参数能够实现自动控制,但是道路坡度大小和长度是随机,且不同的驾驶人驾驶风格差异性较大,该方法适用性较差。
基于以上研究状况和存在问题,本研究依托京昆高速雅安-西昌段典型山区路况试验,提出包含制动踏板状态、道路特征和车辆行驶状态参数的重型载货汽车长下坡制动工况构建及基于滚动时间窗的神经网络辨识方法,构建适用于重型载货汽车山区道路的制动工况和辨识模型,为重型载货汽车长下坡制动电气化智能控制提供依据。
1长下坡制动工况构建
1.1制动短行程定义与划分
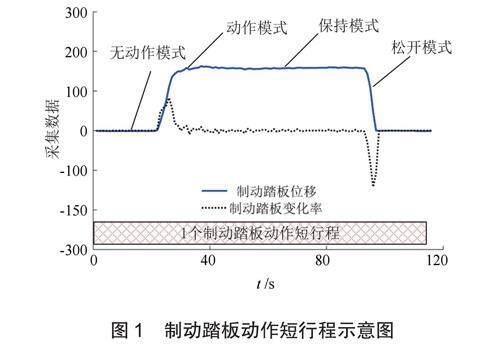
传统循环工况中短行程通常是指从车辆运行的一个怠速时刻开始到下一个怠速开始时刻之间的运行过程[5]。由于重型载货汽车在长下坡道路行驶时,车辆长时间处在运行状态,传统短行程不能详细体现其制动情况。为拓展工况所包含的车辆运行状态信息,基于传统工况构建中短行程的定义,根据车辆制动行为,本文定义重型载货汽车在长下坡道路运行过程中,从一个制动踏板无动作状态开始到下一个制动踏板无动作状态开始的行驶过程为一个制动短行程,即一次完全制动行为,称“制动踏板动作短行程”,如图1所示。一个制动踏板动作短行程同样包含4种模式,具体如表1所示。
本研究基于京昆高速雅安―西昌段典型山区路段车辆道路试验数据开展制动工况构建方法研究,试验路段左线和右线全长约298km,垂直落差将近1600m,大于2%纵向坡度道路占58.14%,大于3%纵向坡度道路占27.49%,属于典型的山区长大下坡路段,道路线型统计见图2。试验过程实时获取制动踏板动作参数和车辆运行状态参数。
按照制动踏板动作短行程定义,对试验数据进行划分,并剔除其中上坡制动踏板异常动作等无效短行程,共得到51条制动踏板动作短行程數据。
1.2状态分类
1)片段划分。以片段为数据单位合成工况可以区分道路类型,规避一个制动踏板动作短行程中不同时刻坡度出现较大变化的问题。将制动短行程划分为制动踏板无动作模式、动作模式、动作保持模式、松开模式4种数据片段。依照图3所示流程,共得到866个片段。
2)特征参数选取。车辆下坡行驶过程中,运行速度、制动踏板位移和道路坡度存在强烈的非线性关系,为此文中选择制动踏板位移、坡度和速度参数,通过该参数的特征参数对状态片段进一步划分,相应特征参数如表2。
3)状态分类。为了构建车辆行驶工况,文中对数据片段进行状态分类。针对制动踏板、坡度和速度数据的不同特点,采用不同的方法进行聚类。针对制动踏板动作,首先利用制动踏板位移变化率和制动踏板位移参数进行主成分分析,再进行K聚类,设置聚类数为4,聚类结果如图4。状态1为低制动踏板位移,保持制动状态;状态2为中制动踏板位移,施加制动状态;状态3为中制动踏板位移,解除制动状态;状态4为高制动踏板位移,保持制动状态。
对于坡度特征,由于单个片段时长较短,仅根据片段平均坡度,设置不同步长的区间,对坡度进行分类。设置坡度状态数为3,即小坡度0~2.5%、中坡度2.5%~4.5%、大坡度4.5~6%。分类结果如图5。
考虑到车辆行驶速度变化与制动强度、坡度等因素相关,通过平均速度vm等8项特征参数进行主成分分析,并利用主要特征参数进行状态聚类,设置聚类数为4,聚类结果如图6。状态1为低速匀速行驶;状态2为加速行驶;状态3为减速行驶;状态4为高速匀速行驶。
4)片段状态求解。当前车辆行驶片段t的制动踏板位移状态为Ds(t),坡度状态为is(t),速度状态为vs(t),根据文献[4]中的编码方式,由当前车辆行驶片段t的Ds(t)、is(t)、vs(t)获得当前片段的编码值。
其中:KD制动踏板位移状态数;Ki:坡度状态数。根据式(1),共有48个片段状态,编码状态部分如表3。
5)状态转移概率矩阵。车辆从某时刻状态变化到下一时刻某一状态的过程称为状态转移。对于车辆行驶片段构成的Markov过程,全部片段状态之间的一步转移概率组合形成状态转移概率矩阵P,如式(2)。
其中,pij表示从片段状态i一步转移至片段状态j的状态转移概率。
本文对48个状态的片段以及相邻2个片段的状态关系进行统计,根据出现的频率计算概率,得出不同状态之间的转移概率为
其中,Nij为片段状态从状态转移到状态j的频数,pij为从状态i转移至状态j的转移概率。
根据式(2)和(3)获得3个参数运行工况片段的状态转移概率矩阵,其二维投影如图7所示。ct表示当前行驶片段状态,ct+1表示下一行驶片段状态。实心圆的大小表示当前行驶片段状态ct转移到下一时刻状态ct+1的概率。根据车辆运行特点,车辆行驶时保持自身状态及其向相邻状态转移的概率最大,沿着状态转移概率矩阵二维投影图45°角平分线上分布。
1.3制动工况构建
重型载货汽车长下坡制动过程中,制动踏板动作、道路坡度与车速变化存在明显的因果关系,前一片段特征参数与后一时刻片段状态变化具有明显的时序性关系。但是,后一时刻片段的状态取决于当前时刻的状态,车辆在长下坡制动时,制动踏板位移从零开始,即车辆制动时制动踏板位移是从无动作状态开始然后到动作状态,或者继续保持无动作状态,因此,Markov理论在起始片段的确定上存在一定的欠缺。为此文中采用Markov-MonteCarlo模拟的方法克服先验不足的问题,以车速平均值为依据,选择与其差的绝对值最小的片段作为起始片段,坡度起始片段不予考虑。
运用Markov-MonteCarlo模拟方法生成符合状态转移概率矩阵的随机数组,由此来确定后续状态,并在对应片段集合选取最合适片段作为下一最优片段。具体过程为:设片段共有n个状态,当前状态为i,下一状态为j,则从状态转移至状态j的概率为Pij。状态转移矩阵的性质可知其每一行概率和为1,即式(4)
利用MATLAB中rand函数命令生成[0,1]之间符合均匀分布的随机数x,如果随机数符合式(5),则下一状态就为k。将所属状态k的片段中,依据制定规则确定下一最优片段,并给k赋值i。重复步骤合成工况,直到达到设定的总时长。
以制动踏板位移、坡度和速度下一片段首位点与当前片段末位点差值绝对值之和最小值确定最优片段,如式(6),记录其位置标号,并将其从片段集中剔除,以防止重复选择片段。
其中:Dt+1,it+1,Vt+1分别为制动踏板位移、道路坡度、速度下一片段首位点,Dt,it,vt分别为制动踏板位移、道路坡度、速度当前片段首位点,asum为绝对值之和。
重复上述过程,直至工况长度满足设定时长且最终制动踏板位移为零,完成一条候选工况构建,重复上述过程完成一定数量的候选工况构建,构建流程如图8。本文共构建100条时长为1200s的重型载货汽车长下坡制动工况。
2.1Markov特性
Markov过程是典型的随机过程,具有“无后效应”。假设X是随时间t变化的连续随机过程,下一状态Xt+1只与当前状态Xt有关,与当前状态之前的其他状态无关。“无后效应”的强弱用相关系数表示。对于一个状态序列{X},长度为L,取{X}中[1:L-k]个状态分量构成新状态序列{X1},取{X}中[k-1:L]个状态分量构成新状态序列{X2}。当状态转移间隔k较小时,{X1}与{X2}的相关系数较大,{X}受相邻位置状态影响明显;随着状态转移间隔k增大,{X1}与{X2}的相关系数变小,{X}受相邻位置状态影响减弱。
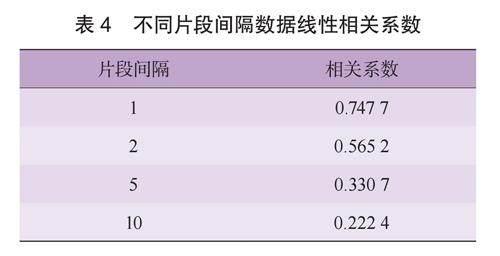
文中采用制动踏板位移、道路坡度和车速三参数构建时间连续Markov过程工况片段,分别选取片段間隔为1、2、5、10构造新状态序列{X1}和{X2},片段如图9,不同片段间隔数据线性相关系数如表4。
为了定性分析不同片段间隔对{X1}与{X2}相关性的影响,采用Pearson相关系数进行评价,如式(7)。
不同片段间隔下新状态序列的相关系数,如表4,当状态转移间隔k较小时,{X1}与{X2}的相关系数较大,说明当前片段状态受相邻位置处的状态影响明显;随着状态转移间隔k增大,{X1}与{X2}的相关系数变小,说明当前片段状态受相邻位置处的状态影响减弱,因此具有“Markov性”,其Markov过程合理。
2.2典型工况选取
为了解决Markov-MonteCarlo方法构建的工况的差异性,本文通过多次构建不同候选工况,从中选出与总体数据差异最小的工况构建典型工况。如表5所示,针对制动踏板位移、坡度、速度3个参数,共选取了22个具有统计意义的特征参数作为工况评估指标,工况评估指标之间的权重相同。
由式(8)与式(9),根据候选工况与总体数据各项特征参数的偏差δ及其均值确定工况,以偏差均值最小的工况构建典型工况。
其中,θi为候选工况第i类特征参数,θ为总体数据特征参数,δi为第i类特征参数偏差,δ?为候选工况偏差均值。
依据上述方法构建的典型工况,如图10。为使数据可视化,将道路坡度信息与速度和制动踏板位移同步转化为海拔高度随行驶时间的变化序列,如图11。获得典型工况数据与总体数据特征参数对比如表6。
经对比分析,文中构建的典型工况数据与总体数据的偏差均值为5.66%,其时长为1238s,制动踏板平均位移为5.93mm,工作时长1194s,平均车速为65.34km/h,运行里程为21.18km,高差为757.10m,符合重型载货汽车长下坡制动运行的特征。重型载货汽车长下坡制动工况制动踏板位移范围0~15mm,坡度范围为0~6%,速度范围为55~80km/h。
3制动工况辨识
3.1制动工况标准数据库建立
标准数据库采用K聚类方法建立,依据工况特征参数建立聚类分析与反向传播(backpropagation,BP)神经网络模型。考虑到制动工况特征参数较多,聚类边界不明显,为此通过特征参数之间的Pearson相关系数选取特征参数,如式(7)所示,部分结果如表7。
通常,Pearson相关系数0.8以上,两者间有极强的相关性;0.6~0.8,有强相关性;0.4以下,有弱相关性或者没有相关性。据此,选择平均制动踏板动作位移Dom、最大制动踏板位移Dmax、平均制动踏板踩踏变化率Gsm、平均制动踏板位移松放变化率Glm4个特征参数,用于聚类分析与建立工况识别模型。
设置聚类状态数K为3,聚类结果如图12,横坐标为平均制动踏板动作位移Dom,即短行程内制动踏板动作状态下的位移平均值,纵坐标为短行程内最大速度与短行程末速度的差值Δv2,反映一个制动踏板动作短行程(一次制动行为)的制动效果。聚类结果分为3类,即弱制动工况,一般制动工况,强制动工况,每类工况各参数统计值见表8。
由表8,工况1制动踏板位移平均值与制动踏板位移最大值均处于较低水平,制动强度较弱,其短行程初速度与末速度差值为负值,呈现加速状态;工况3制动踏板位移平均值与制动踏板位移最大值均处于较高水平,制动强度较强,其短行程初速度与末速度差值为正值,呈现减速状态;工况2制动踏板工作位移平均值与制动踏板位移最大值均处于工况1与工况3之间,制动强度处于一般水平,短行程初速度与末速度差值接近于零,整体呈现匀速状态。
综上所述,定义以上工况为加速弱制动工况,其特征如工况1所述;匀速一般制动工况,其特征如工况2所述;减速强制动工况,其特征如工况3所述。为简化工况特征,忽略坡度特性。
3.2工况模型训练
BP神经网络属于多层前向网络,具有复杂非线性映射、自学习能力,可用于求解内部机制复杂的问题,且不会随数据量增大增加计算量,为此利用BP网络建立制动工况识别模型。基本结构如图13,由输入层、隐含网络层与输出层组成,不同层之间通过具有一定权值与阈值的神经元连接。前向传播由输入层至输出层逐层处理;如不能得到期望输出,通过误差逆向反馈,并以此对权值和阈值进行更新,迭代使输出与期望值之间的误差越来越小,以此训练神经网络模型。
设置学习效率η为0.0015,目標误差为0.01,最多训练次数为200万次,中间神经元的数量为12,进行神经网络训练。针对本文数据块数量特点,采用训练集与测试集7:3将工况块分类,即70%的样本作为训练集,工况1、工况2、工况3数量分别为4组、62组、191组;30%样本作为测试集,工况1、工况2、工况3数量分别为4组、28组、83组。
3.3工况辨识与在线验证
为了验证构建工况的准确性,选取训练集和验证集数据进辨识验证,测试集和验证集神经网络识别率达到100%,可以用于构建工况的识别,验证结果如图14和图15。
为了保证在线识别的时效性,采用滚动时间窗识别策略,根据时间窗宽度内制动踏板动作数据,识别当前制动工况,以一定时间步长向前滚动采集制动踏板动作数据,实现对制动工况的持续识别。依据短行程片段进行定步长辨识,如图16。
为提高识别精度,选择合理时间步长,分别选取10、20……120s时间窗宽度以确定最优步长,比较结果如图17,时间窗宽度60s时识别准确性最高,为此文中选取识别步长为60s。
以60s为步长对工况块化处理,将其输入至神经网络,其识别结果如图18所示。
依据表9对构建工况序列进行工况状态赋予,如表9,验证状态如图19所示。
构建工况识别与状态赋予结果对比如图20。定步长工况块识别一般制动工况和强制动工况正确率为89.30%。
4结论
文中以山区公路行驶试验数据为基础,利用短行程划分、K聚类和编码技术建立了重型载货汽车长下坡行驶工况,并对辨识方法展开研究。
以车辆行驶速度、制动踏板位移和道路坡度等特征参数对短行程数据进行统计分析,得到在山区公路行驶车辆的典型运动学片段,分析了片段间的Markov特性并利用Markov-MonteCarlo模拟方法弥补了Markov先验不足的缺点,依据具有统计意义的特征参数对候选工况进行评估,最终得到重型载货汽车长下坡制动工况,工况总时长1194s,长度21.18km。
以一定时间步长向前滚动实现对制动工况的持续识别,时间窗宽度60s时识别准确性最高;为了验证重型载货汽车长下坡制动工况识别模型的准确性,依据工况特征在线辨识,结果显示一般制动工况和强制动工况正确率为89.30%,研究表明建立的工况识别模型可有效对制动工况进行识别。
下一步开展典型工况与特征参数权重的映射关系及基于长下坡制动工况辨识的制动控制策略研究。
