BDS/GPS PPP固定解精度分析及其在地震中的应用
2023-04-28黄剑明李敬伟杨南南张鸿洋徐宗秋
黄剑明,庄 典,李敬伟,杨南南,张鸿洋,徐宗秋
BDS/GPS PPP固定解精度分析及其在地震中的应用
黄剑明1,庄 典1,2,李敬伟3,杨南南1,张鸿洋1,徐宗秋1
(1. 辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000;2. 沈阳市勘察测绘研究院有限公司,沈阳 110000;3. 河北省国土整治中心,石家庄 050002)
为了提高北斗卫星导航系统(BDS)和全球定位系统(GPS)精密单点定位(PPP)性能,提出一种BDS/GPS PPP固定解精度分析方法:采用无电离层组合PPP模型,给出基于未校准相位延迟(UPD)估计的PPP模糊度固定(AR)方法;并分析将动态PPP AR应用于估计地震中全球卫星导航系统(GNSS)测站位移量的可行性。实验结果表明,UPD产品估值相对稳定,利用该UPD产品可实现BDS/GPS PPP AR,提高PPP定位性能,其中,BDS/GPS组合动态PPP收敛时间在东(E)、北(N)和天(U)方向上分别为15、12.5和20 min,其固定解在3个方向上的定位精度可达1.52、1.34和2.81 cm,较浮点解分别提升12.6%、5.6%和9.4%;利用BDS/GPS动态PPP AR分析青海地震中清水河站(QSHZ)测站位移量,验证了BDS/GPS PPP AR可实现厘米级地震位移监测。
精密单点定位(PPP);未校准相位延迟;模糊度固定(AR);收敛时间;定位精度;地震
0 引言
近年来,全球卫星导航系统(global navigation satellite system,GNSS)的快速发展为提高定位性能创造了条件[1-2]。精密单点定位(precise point positioning,PPP)采用单台GNSS接收机,利用国际GNSS服务组织(International GNSS Service,IGS)提供的精密星历和卫星钟差,能达到全球静态毫米级、动态厘米到分米级的定位能力。PPP具有单机作业,不受作业距离的限制,数据利用率更高等优势[3-4],广泛应用于航空测量、海洋测量和地震位移监测等领域。但是由于模糊度参数部分难以固定,严重影响了PPP的定位精度和收敛速度,在一定程度上限制了PPP在相关领域内的深入应用。研究表明,在卫星端和接收机端都存在着未校准相位延迟(uncalibrated phase delays,UPD),且很难将它们与模糊度参数分离,导致模糊度参数丢失整数特性而无法快速固定[5-6]。因此,如何分离PPP模糊度中的UPD并精确估计及校正是实现PPP模糊度固定(ambiguity resolution,AR)的重要前提,也是实现GNSS高精度定位的关键[7]。
PPP比双差定位模型估计了更多的待估参数,其中,接收机钟差、电离层延迟、接收机伪距频间偏差(differential code biases,DCBs)、模糊度之间具有较强的相关性[8];另外,当有新的卫星出现以及周跳或数据中断发生时,部分模糊度参数不再收敛,如何正确固定所有模糊度参数就变得十分困难[9-10]。将模糊度参数恢复为整数的主要方法包括利用小数周偏差产品(fractional cycle bias,FCB)、钟差去藕模型法(decoupled clock model,DCM)以及整数钟法[11-13]。有研究表明,利用正则化方法可以解决北斗卫星导航系统(BeiDou navigation satellite system,BDS)单历元进行整周模糊度解算中存在的法方程秩亏问题,并得到较准确的模糊度浮点解,使单历元模糊度固定成功率达到100%[14]。北斗三号全球卫星导航系统(BeiDou-3 navigation satellite system,BDS-3)进行多频相位模糊度解算,可有效进行单历元模糊度固定,同时频率数增加可显著提高模糊度固定成功率[15]。BDS星间单差UPD在连续时段内具有一定的稳定性,时长越短模糊度固定率越低,固定解精度提高越显著,较浮点解定位精度均提高12%以上[16]。对BDS、全球定位系统(global positioning system,GPS)和BDS/GPS组合进行PPP AR的结果表明,BDS的AR的首次固定时间(time to first fix,TTFF)大于6 h,而GPS/BDS AR组合的静态和动态PPP的TTFF分别为16.9和24.6 min[17]。在PPP固定解技术的实际应用中,有一种位置聚类法对短时间的静态PPP固定解结果进行优化的方法,优化结果在东(E)、北(N)、天(U)方向的定位精度分别为3.03、0.92、3.39 cm,较浮点解和固定解均有厘米级的精度提升[18]。
本文首先估计了BDS/GPS的UPD,主要从UPD稳定性、残差、数据利用率等方面对UPD产品质量进行评估;然后,利用估计的UPD进行PPP模糊度固定,研究BDS/GPS静态PPP AR定位精度,并重点研究BDS/GPS动态PPP AR首次固定时间、固定百分比、收敛时间和收敛后定位精度;最后,分析PPP AR在监测地震测站位移量方面的应用。
1 数据处理原理
1.1 PPP函数模型
PPP中常采用双频消电离层组合模型消除电离层一阶项误差的影响。采用双频伪距和载波相位观测值进行消电离层模型组合的数学模型为:


1.2 UPD估计模型
在无电离层组合PPP函数模型中,由于受到卫星端初始相位、相位观测值信号延迟、伪距观测值群延迟和实数伪距基准等因素的影响,非差观测方程中模糊度不再具有整数特性。因此,PPP整周模糊度固定的关键是有效分离模糊度参数中的小数部分和整数部分,恢复模糊度整数特性。对于无电离层组合模糊度通常分解为宽巷(wide lane,WL)和窄巷(narrow lane,NL)模糊度依次尝试固定。WL模糊度是根据墨尔本-维贝纳(Melbourne-Wübbena,MW)组合计算得出,而NL模糊度是从整数WL模糊度和PPP估计的无电离层组合模糊度得出。WL和NL的模糊度可表示为:

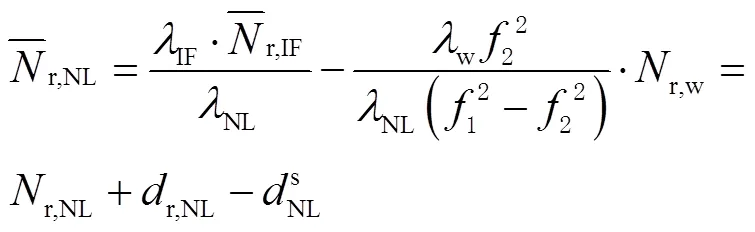
基于单站PPP浮点解获取非差WL和NL模糊度估值,然后在UPD估计过程中,利用迭代最小二乘对所有测站的输入模糊度参数统一处理。对于任一连续观测弧段WL和NL浮点模糊度都可表达为
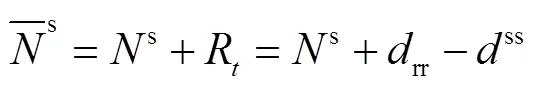
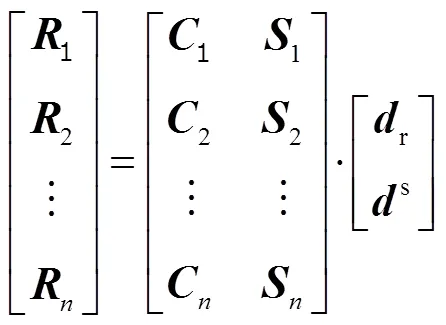
获得UPD产品后可进行PPP AR,过程如下:
1)基于MW组合观测值计算WL浮点模糊度,并形成星间单差WL模糊度,利用WL UPD改正WL模糊度。WL模糊度因为波长较长,且与观测误差和测量噪声关联不大,所以WL模糊度固定一般直接采用取整法。
2)PPP解算,获得无电离层组合模糊度。将星间单差WL整数模糊度代入由无电离层组合模糊度分解为WL和NL模糊度的线性组合方程,求出星间单差浮点NL模糊度,并利NL UPD进行改正。由于窄巷模糊度相关性较强,NL模糊度固定通过最小二乘模糊度降相关平差方法搜索得到。
3)将NL模糊度参数固定为整数之后,基于混合整数最小二乘参数估计方法获得PPP模糊度固定解。
2 实验与结果分析
2.1 UPD估计结果与分析
2.1.1 UPD稳定性
在精密轨道与钟差产品方面选择德国地学研究中心(Deutsches GeoForschungs Zentrum,GFZ)提供事后多GNSS精密钟差(GFZ multi-GNSS precise clock,GBM)的产品,GBM最新产品包含了BDS-3所有卫星的轨道与钟差数据。选择全球范围128个多模GNSS实验跟踪网(multi-GNSS experiment,MGEX)测站2021年年积日(day of year,DOY)第102—108天的观测数据,测站均匀分布全球各地,下载30 s采样率的观测数据,用于估计BDS和GPS卫星UPD产品。由于地球同步轨道(Geostationary Earth Orbit,GEO)卫星轨道精度较低,未估计GEO卫星的UPD。每天估计一组WL UPD,每历元估计一组NL UPD。2021年DOY第102—108天7 d 的WL UPD和2021年DOY 第103天1 d 的NL UPD估计结果如图1所示。
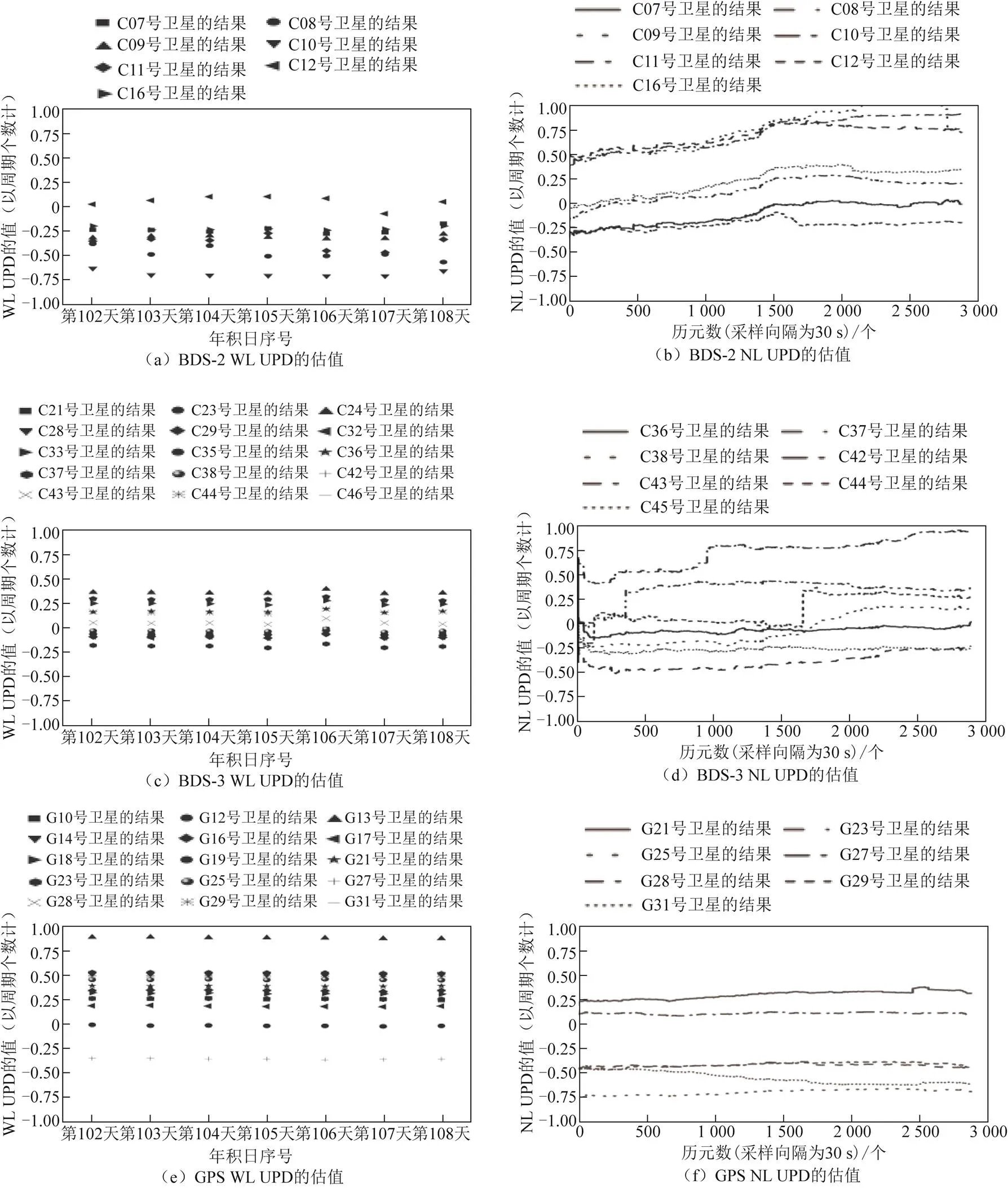
图1 BDS-2、BDS-3、GPS WL和NL UPD估值结果
以22颗BDS卫星、15颗GPS卫星的UPD估计结果为例,北斗卫星导航(区域)系统即北斗二号(BeiDou navigation satellite (regional) system,BDS-2)、BDS-3、GPS的参考卫星分别为C13、C19、G26卫星。总体来看,BDS-3卫星的WL UPD估计结果和稳定性均优于BDS-2卫星,而GPS卫星则明显优于BDS卫星;BDS-2卫星的NL UPD估计值在1 d中相对比较稳定。从图1(d)中(仅挑选部分卫星)可以看出,C42、C43和C44卫星NL UPD出现较大幅度波动,其余BDS-3卫星NL UPD序列相对平稳;如图1(f)(仅挑选部分卫星)所示,GPS卫星的NL UPD估计值在1 d中非常稳定。
2.1.2 UPD残差
将UPD从模糊度中分离后,模糊度参数与整数值的偏差为UPD估计的残差,UPD的残差分布也是检核UPD一致性的重要指标之一。2021年DOY 第103天的BDS-2、BDS-3和GPS卫星UPD产品估计的验后残差分布结果如图2所示。对于BDS-2、BDS-3、GPS卫星的WL UPD残差,分布于±0.15个周期以内的残差分别为85.19%、96.19%和94.88%,分布于±0.25个周期以内分别为99.79%、99.96%和99.87%;对于NL UPD残差,则分布于±0.15个周期以内的分别为80.36%、78.9%和80.71%,分布于±0.25个周期以内分别为99.59%、99.51%和99.16%。实验结果表明,估计的BDS和GPS卫星UPD产品估值相对稳定,良好稳定的UPD产品为接下来的PPP AR奠定了基础。
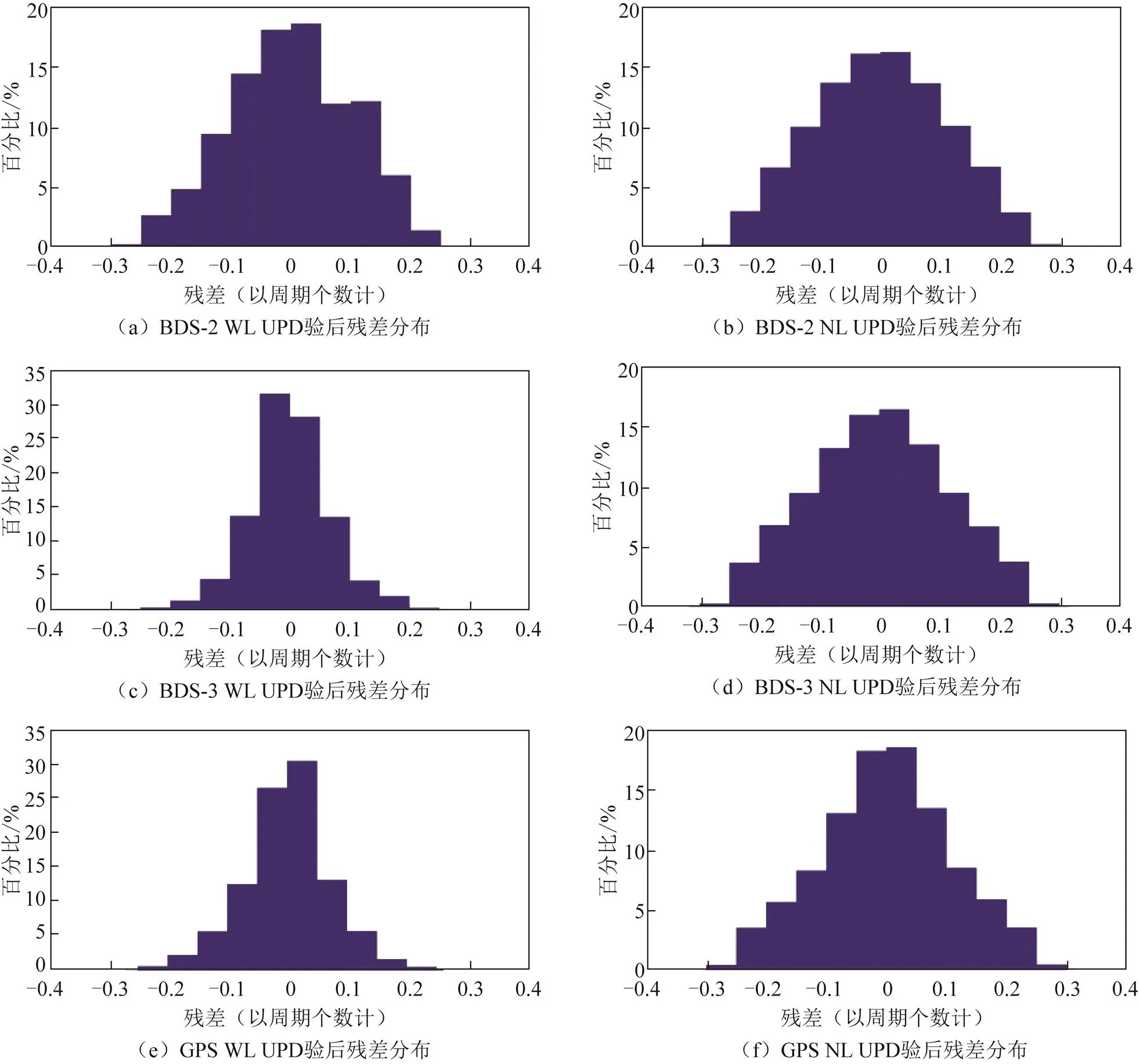
图2 BDS-2、BDS-3、GPS UPD验后残差分布结果统计
2.1.3 数据利用率
数据利用率是衡量UPD产品内符合性的重要指标之一,其定义为用于UPD估计的模糊度个数与所有模糊度个数的比值。利用128个MGEX测站估计BDS-2、BDS-3和GPS卫星WL UPD和NL UPD产品,数据利用率如图3所示。WL UPD平均数据利用率方面,BDS-2、BDS-3和GPS分别为73.3%、83%和89.9%;NL UPD方面,则分别为67.4%、74.5%和81.1%。显然,BDS-3卫星的UPD数据利用率略高于BDS-2卫星,GPS卫星的UPD 数据利用率最高。
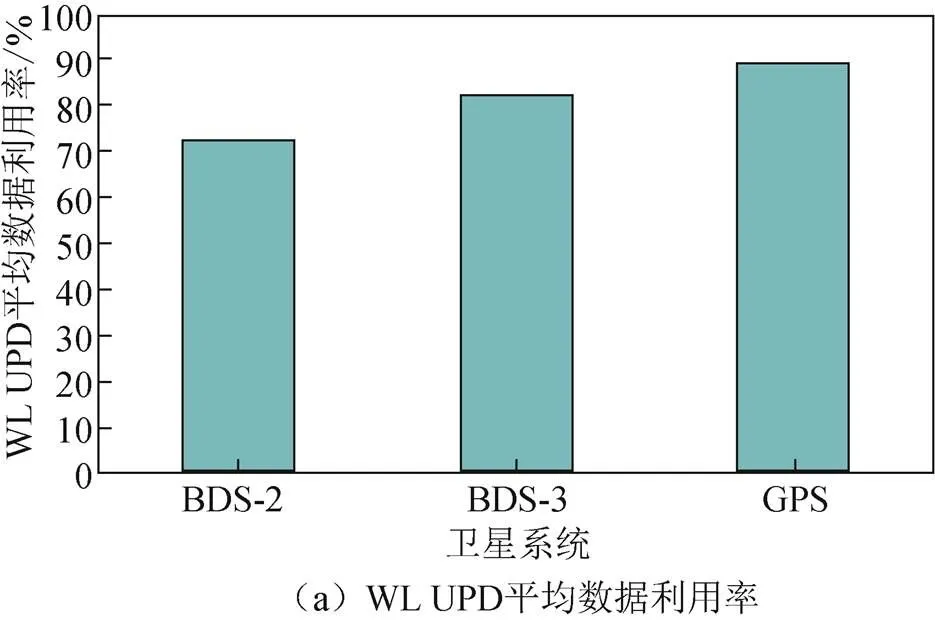
2.2 PPP AR结果与分析
基于上述UPD产品,利用相应的观测值文件、精密轨道和钟差等进行PPP AR实验。PPP实验选取未参与UPD估计的10个MGEX测站(brst、ganp、krgg、mayg、mch1、parc、ptgg、rgdg、str2、unb3)2021年DOY第102—108天的GNSS观测数据,数据采样率为30 s,在精密轨道与钟差产品方面选择GBM提供的产品,站点坐标以IGS中心发布的周解文件中坐标作为参考值。实验数据处理策略如表1所示。利用上述数据及处理策略分别开展了BDS、GPS以及BDS/GPS组合的PPP AR静态和模拟动态实验。

表1 PPP数据处理策略
2.2.1 BDS、GPS、BDS/GPS静态定位结果与分析
以IGS中心发布的周解文件中坐标作为参考值,分析静态模式下PPP固定解的定位性能。静态PPP将最后一个历元的绝对定位误差值作为定位精度。10个测站3种卫星系统模式下静态PPP的定位误差结果如表2和图4所示。从平均统计结果来看,固定解定位精度均优于浮点解,少数测站的PPP固定解N方向定位精度比浮点解略有降低,但降低值均不超过0.2 mm。BDS静态PPP固定解E、N和U方向平均定位精度分别为0.35、0.25和1.17 cm,较浮点解分别提高了14.6%、7.4%和11.4%,E方向定位精度提升明显;而GPS和BDS/GPS组合静态PPP固定解E和U方向定位精度提升明显;BDS/GPS组合固定解平均定位精度最优,GPS平均定位精度略优于BDS。

表2 3种卫星系统模式下静态PPP平均定位误差结果统计
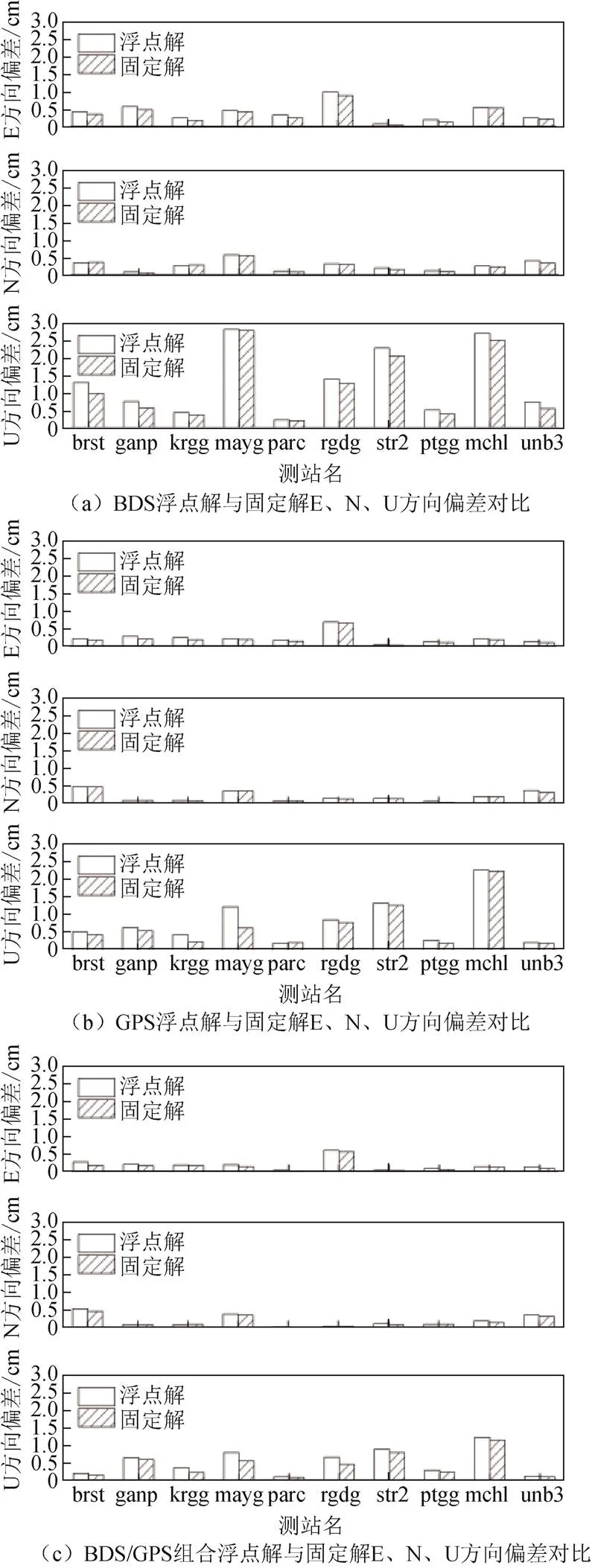
图4 3种卫星系统模式下静态PPP定位误差结果统计
2.2.2 BDS、GPS、BDS/GPS动态定位结果与分析
以IGS中心发布的周解文件中坐标作为参考值,分析模拟动态模式下PPP固定解的定位性能。为了详细分析动态PPP AR定位性能,从首次固定时间、模糊度固定百分比、收敛时间和定位精度 4个方面进行评估。实现模糊度首次成功固定的时间即为首次固定时间。模糊度固定百分比的定义为成功固定的历元数与实现首次固定后的历元数的比值。动态PPP的收敛时间定义为E、N、U定位偏差均优于0.1 m,且当连续20个历元的偏差都在限值以内时,才认为PPP解在当前历元收敛。动态PPP定位精度为收敛后定位偏差的均方根。对每个测站7 d的统计结果取均值,分析PPP定位性能。
1)TTFF及模糊度固定率。10个测站3种卫星系统模式下动态PPP TTFF及模糊度固定率结果统计如表3和表4所示。以单测站为例,最快的TTFF为BDS和BDS/GPS组合系统模式下的ptgg站,为13.5 min,最慢的TTFF为BDS模式下的unb3站,为31 min。BDS、GPS以及BDS/GPS组合平均TTFF分别为22、21和19.5 min。BDS/GPS组合加快了模糊度首次固定时间。在BDS动态PPP模糊度固定率方面,除了krgg测站,其余测站模糊度固定率均低于80%,模糊度固定率较低;在GPS、BDS/GPS组合2种模式下,除了ganp测站和mchl测站外,其余测站模糊度固定率均在85%以上,最高为GPS模式下的str2测站,高达94.4%。BDS、GPS以及BDS/GPS组合平均模糊度固定率分别为73.1%、88.9%和87.7%。
2)收敛时间。在3种卫星系统模式下,动态PPP在3个方向上的平均收敛时间结果如图5所示。BDS在E、N和U方向平均收敛时间分别为16、14和23 min,GPS分别为16、12和21.5 min,BDS/GPS分别为15、12.5和20 min。整体上BDS/GPS组合收敛速度最快。

表3 3种卫星系统动态PPP模式下10个测站TTFF及模糊度固定率结果统计

图5 3种卫星系统模式下动态PPP平均收敛时间

表4 3种卫星系统动态PPP模式下10个测站平均TTFF、平均模糊度固定率结果统计
3)定位误差。10个测站在3种卫星系统模式下,动态PPP的定位误差结果如表5和图6所示。对于BDS模糊度固定解,大部分测站的固定解精度均有提升,E方向提升率最高,其中ptgg测站的E方向提升率高达48.6%。GPS模拟动态PPP固定解,3个方向提升幅度均不超过10%。模拟动态PPP模糊度固定解定位精度均优于浮点解,BDS/GPS组合定位精度优于单系统定位精度。

表5 3种卫星系统模式下动态PPP平均定位误差结果统计
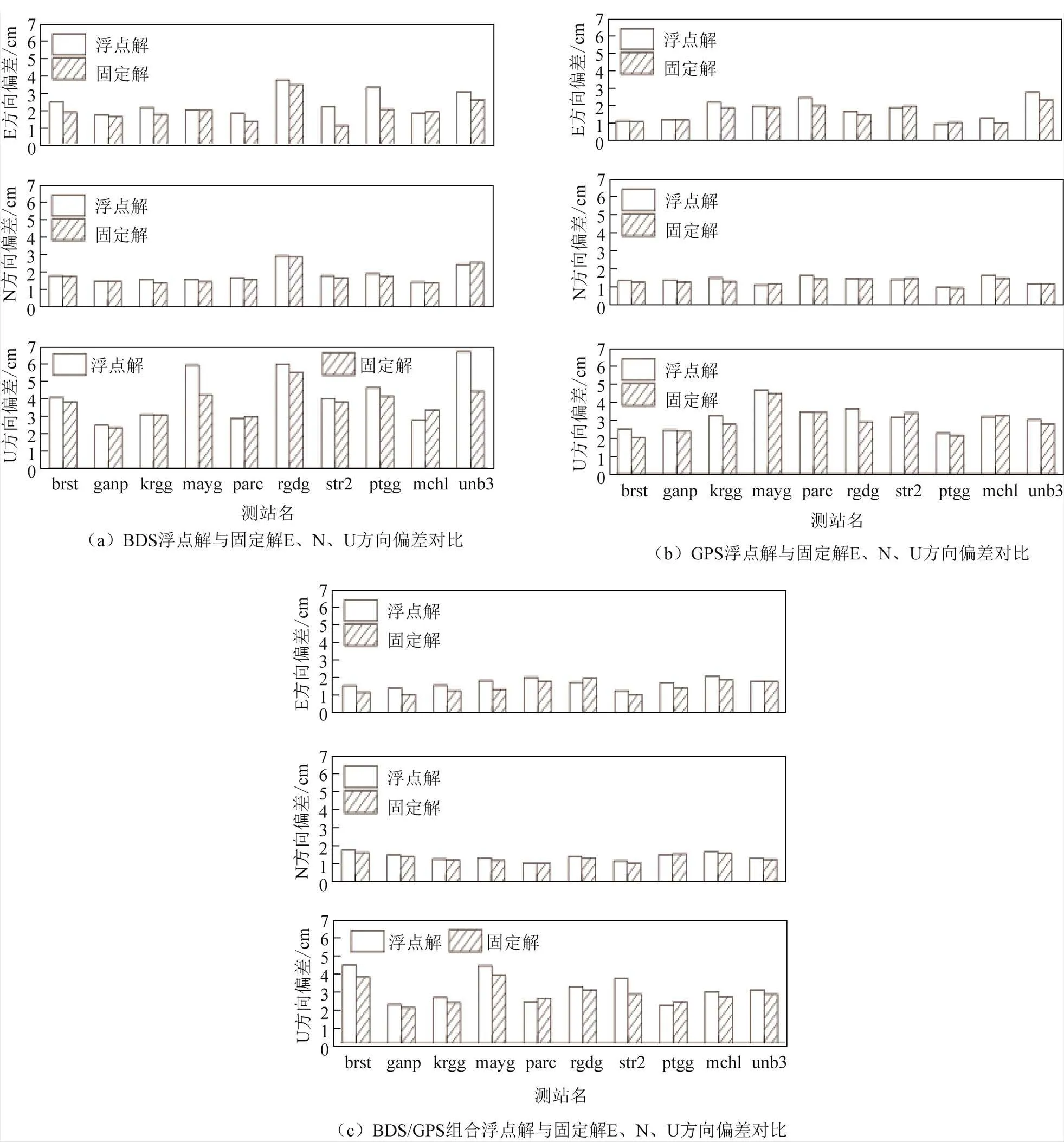
图6 3种卫星系统模式下动态PPP定位误差结果统计
3 青海果洛州玛多县地震清水河站位移量分析
据中国地震台网测定,2021年5月22日2时4分,也就是2021-05-21协调世界时(universal time coordinated,UTC)18:04,在青海果洛州玛多县(北纬34.59°,东经98.34°)发生7.4级地震,震源深度17 km,震中10 km范围内平均海拔约4200 m。利用动态BDS/GPS PPP AR技术处理距离震中140 km左右清水河站(Qing Shui He Zhan,QSHZ)GNSS数据,估计地震使测站的位移量。分别统计震前(15 min)和震后(15 min)定位误差序列的标准差(standard deviation,STD)和平均偏差作进一步分析。QSHZ测站在3种模式下,地震前、后定位误差序列统计结果如表6所示。BDS PPP AR定位误差序列在E和N方向上地震前、后的STD为2~4 mm,地震后在E和N方向上的位置偏移量分别为21和12 mm;U方向误差序列地震前、后的STD分别为7和9 mm,数值与U方向偏移量11 mm接近。GPS动态PPP AR STD水平方向上达5~7 mm,高程方向上达13~15 mm。BDS/GPS动态PPP AR重复性定位精度水平方向上达3~4 mm,高程方向上达9 mm。
图7为地震期间QSHZ测站水平运动轨迹。从图7可以看出,3种结果均表明在地震期间QSHZ测站发生了明显的水平位移,且运动方向趋势相似,测站位置从缓慢移动到剧烈移动,最后恢复平稳。由BDS PPP AR解算结果可以看出,QSHZ测站发生了可恢复性的弹性形变,最大达到10 cm。平稳后测站发生的永久性水平位移约为2.4 cm。研究成果可为GNSS动态PPP AR技术用于监测地震测站位移量提供参考。

表6 地震前、后定位误差序列统计 m
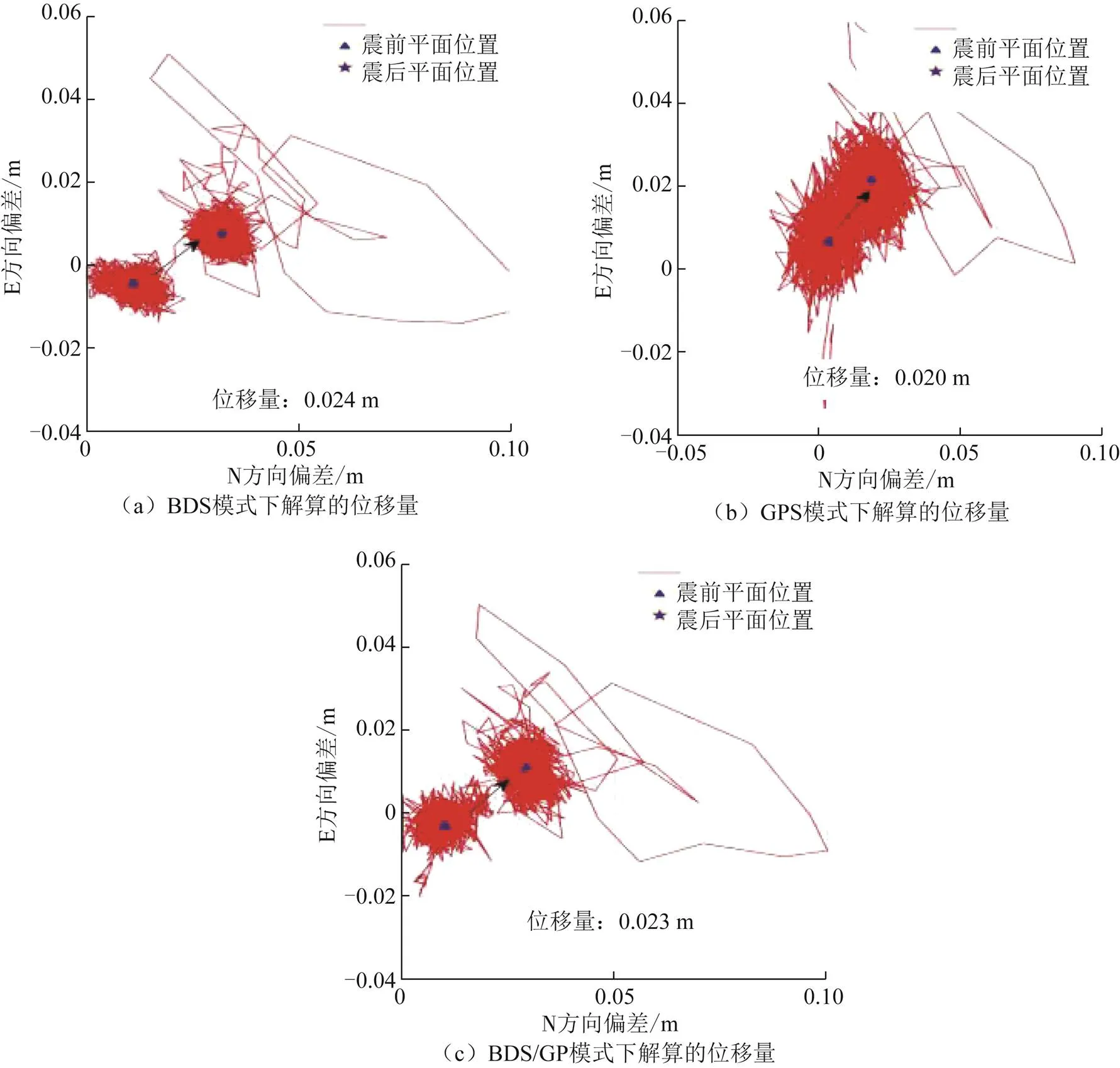
图7 地震期间QSHZ测站水平运动轨迹
4 结束语
本文选取全球范围128个MGEX测站估计UPD产品,之后选取10个未参与估计UPD产品的MGEX测站进行PPP AR实验,分析BDS、GPS、以及BDS/GPS组合PPP AR静态、模拟动态定位性能,另外,利用动态BDS/GPS PPP AR技术分析了青海地震使距离震中140 km左右QSHZ测站产生的位移量,结果表明:
1)UPD产品估值相对稳定,利用估计的UPD产品进行静态和动态PPP AR,实现了定位性能的提高。其中,BDS/GPS组合静态PPP在E、N和U方向上的固定解定位精度分别为0.16、0.17和0.43 cm,较浮点解分别提高了20%、10.5%和18.9%。BDS/GPS组合模拟动态PPP 3个方向的固定解定位精度分别为1.52、1.34和2.81 cm,较浮点解分别提高了12.6%、5.6%和9.4%。
2)BDS、GPS和BDS/GPS组合模拟动态PPP平均TTFF分别为22、21和19.5 min,平均模糊度固定率分别为73.1%、88.9%和87.7%。BDS/GPS组合动态PPP较单系统加快了收敛速度,其E、N和U方向收敛时间分别为15、12.5和20 min。
3)将BDS/GPS动态PPP AR技术用于分析地震中QSHZ测站的位移量,结果表明,QSHZ测站地震中发生了可恢复性的弹性形变,最大达到10 cm。平稳后测站发生的永久性水平位移约为 2.4 cm。验证了动态PPP AR可用于监测地震中GNSS监测站厘米级位移量。
[1] MONTENBRUCK O, STEIGENBERGER PRANGE L. The multi-GNSS experiment (MGEX) of the international GNSS service (IGS) achievements, prospects and challenges[J]. Advances in Space Research, 2017, 59(7): 1671-1697.
[2] 赵昂, 杨元喜, 许扬胤, 等. GNSS单系统及多系统组合完好性分析[J]. 武汉大学学报(信息科学版), 2020, 45(1): 72-80.
[3] ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5005-5017.
[4] KOUBA J, HEROUX P. Precise point positioning using IGS orbit and clock products[J]. GPS Solutions, 2001, 5(2): 12-28.
[5] LI X X, ZHANG X H. Improving the estimation of uncalibrated fractional phase offsets for PPP ambiguity resolution[J]. Journal of Navigation, 2012, 65(3): 513-529.
[6] LI P, ZHANG X H, GUO F. Ambiguity resolved precise point positioning with GPS and BeiDou[J]. Journal of Geodesy, 2017, 91(1): 25-40.
[7] 孙孝波, 顾天琪, 谷守周, 等. 模糊度固定技术的GPS/BDS-2/BDS-3精密单点定位性能分析[J]. 测绘科学, 2022, 47(4): 26-33.
[8] 伍冠滨, 陈俊平, 伍晓勋, 等. 基于非差非组合PPP-RTK的大气改正模型及其性能验证[J]. 测绘学报, 2020, 49(11): 1407-1418.
[9] 赵兴旺, 张翠英. 精密单点定位部分模糊度固定方法[J]. 中国空间科学技术, 2013, 33(1): 37-44, 68.
[10] 潘宗鹏, 柴洪洲, 刘军, 等. 基于部分整周模糊度固定的非差GPS精密单点定位方法[J]. 测绘学报, 2015, 44(11): 1210-1218.
[11] GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008, 82(7): 389-399.
[12] LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination[J]. Navigation, 2009, 56(2): 135-149.
[13] COLLINS P, BISNATH S, LAHAYE F, et al. Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing[J]. Navigation, 2010, 57(2): 123-135.
[14] 李博, 徐爱功, 祝会忠, 等. 一种BDS单历元整周模糊度固定的解算方法[J]. 导航定位学报, 2018, 6(2): 77-81.
[15] 章浙涛, 李博峰, 何秀凤. 北斗三号多频相位模糊度无几何单历元固定方法[J]. 测绘学报, 2020, 49(9): 1139-1148.
[16] 徐宗秋, 丁新展, 徐彦田, 等. BDS静态精密单点定位模糊度固定解精度分析[J]. 测绘科学, 2019, 44(7): 30-34.
[17] LIU Y, YE S, SONG W W, et al. Integrating GPS and BDS to shorten the initialization time for ambiguity-fixed PPP[J]. GPS Solutions, 2017, 21(2): 333-343.
[18] 罗玉山, 张小红. 利用聚类法实现PPP固定解的快速静态定位[J]. 导航定位学报, 2021, 9(4): 104-109, 136.
Precision analysis of BDS/GPS PPP fixed solution and its application in earthquake
HUANG Jianming1, ZHUANG Dian1,2, LI Jingwei3, YANG Nannan1, ZHANG Hongyang1, XU Zongqiu1
(1. School of Geomatics, Liaoning Technical University, Fuxin, Liaoning 123000, China;2. Shenyang Geotechnical Investigation & Surveying Research Institute Co.Ltd., Shenyang 110000, China;3. Hebei Provincial Land Control Center, Shijiazhuang 050002, China)
In order to improve the precise point positioning (PPP) performance of BeiDou navigation satellite system (BDS) and global positioning system (GPS), the paper proposed a precision analysis method of BDS/GPS PPP fixed solution: a combined PPP model with ionospheric-free was used, and a PPP ambiguity resolution (AR) method based on uncalibrated phase delay (UPD) estimation was given; then the feasibility of applying kinematic PPP AR to estimate the displacement of global navigation satellite system (GNSS) stations in earthquakes was analyzed. Experimental results showed that the valuation of UPD products would be relatively stable, and BDS/GPS PPP AR could be realized by using the UPD product, which helps improve the PPP positioning performance. Among them, the convergence time of BDS/GPS combined kinematic PPP in East (E), North (N) and Up (U) directions would be 15, 12.5 and 20 min, respectively. Moreover, the positioning accuracy of the fixed solution in three directions would be 1.52, 1.34 and 2.81 cm, and compared with the floating solution, the improvement rates would be 12.6%, 5.6% and 9.4%, respectively. Finally, it was verified that BDS/GPS PPP AR could realize cm-level seismic displacement monitoring by using BDS/GPS kinematic PPP AR to analyze the displacement of the Qing Shui He Zhan (QSHZ) station during the Qinghai earthquake.
precise point positioning (PPP); uncalibrated phase delays; ambiguity resolution (AR); convergence time; positioning accuracy; earthquake
P228
A
2095-4999(2023)02-0106-11
黄剑明, 庄典, 李敬伟, 等. BDS/GPS PPP固定解精度分析及其在地震中的应用[J]. 导航定位学报, 2023, 11(2): 106-116.(HUANG Jianming, ZHUANG Dian, LI Jingwei, et al. Precision analysis of BDS/GPS PPP fixed solution and its application in earthquake[J]. Journal of Navigation and Positioning, 2023, 11(2): 106-116.)DOI:10.16547/j.cnki.10-1096.20230212.
2022-05-12
国家自然科学基金项目(42074012,42030109);辽宁省重点研发计划项目(2020JH2/10100044);辽宁省“兴辽英才计划”项目(XLYC2002101,XLYC2008034,XLYC2002098);自然资源部测绘科学与地球空间信息技术重点实验室经费资助项目(2020-1-1)。
黄剑明(1996—),男,福建莆田人,硕士研究生,研究方向为卫星定位与导航。
