导管架平台管节点疲劳裂纹的断裂评估
2023-04-27徐绍勋张勇刘圆田其磊
徐绍勋,张勇,刘圆,田其磊
(1.中海石油(中国)有限公司深圳分公司,广东 深圳 518067;2.中国船级社海洋工程技术中心,天津 300457)
导管架平台长期受到波浪力的循环载荷作用,管节点环焊缝焊趾处的热点应力区易引发疲劳裂纹。疲劳裂纹会在长度和深度方向逐渐扩展,从而导致管节点失效[1-2]。含裂纹管节点的完整性一般根据BS7910[3]采用失效评定图(FAD)进行断裂评估,通过“合于使用”原则判定当前裂纹尺寸是否满足结构安全要求。然而,BS7910的管节点裂纹的断裂评估方法存在不足,该方法没有给出弯曲强度折减系数公式。因此,含裂纹管节点的极限强度的计算没有统一的指南;只给出管节点关键位置处(冠点、鞍点)的应力集中系数公式和应力弯曲度公式,评估时假设裂纹位于这些关键位置,导致评估结果非常保守。此外,也没有给出贯通裂纹的应力强度因子公式。
疲劳裂纹的断裂评估同时考虑断裂失效和塑性失效。断裂评估需计算断裂比Kr和荷载比Lr。其中Kr是应力强度因子和断裂韧性的比值;Lr是荷载和极限强度的比值。含裂纹管节点极限强度的计算需考虑裂纹面积对轴向承载面积和塑性剖面模数的影响,对完好管节点的极限强度进行折减。BS7910只给出含裂纹管节点的轴向强度折减系数,没有给出含裂纹管节点的弯曲强度折减系数公式。弯曲强度折减系数公式应该根据裂纹面积对管节点塑性弯矩的影响进行推导,但相关的研究非常有限。大多数研究者都试图对试验结果或有限元分析数据进行拟合,提出含裂纹T/Y型[4-8]、K型[9]、DT型[10]等节点形式的弯曲强度折减系数的经验公式。但是这些经验公式中,弯曲强度折减系数都表达为裂纹面积的线性函数,和塑性剖面模数没有直接关系。另外,不同的管节点形式对应不同的公式,尚未实现统一,并且大多数公式都保守地假设裂纹位于鞍点或冠点。导管架管节点受轴向荷载、平面内弯矩和平面外弯矩的共同作用,因此弯曲强度折减系数的通用公式对极限强度的计算非常重要,该公式需直接考虑裂纹面积对塑性剖面模数的影响。因此,基于净截面破坏(NSC)准则,提出含裂纹管节点受平面内和平面外弯矩作用的弯曲强度折减系数公式,该公式可以考虑位于焊缝任何位置的裂纹,并考虑裂纹扩展的不同阶段,即裂纹全部位于截面受拉应力区域和裂纹部分位于受压应力区域。
大量的管节点疲劳试验研究表明,管节点的疲劳寿命和断裂性能不但依赖于热点应力,而且与裂纹处厚度方向的应力分布有很大关系,应力弯曲度是裂纹处厚度方向的弯曲应力和总应力的比值,该比值可以用来代表厚度方向的应力分布;很多研究者通过大量的有限元分析拟合,推导出应力弯曲度的经验公式[11-16]。但是,多数文献只给出节点关键位置处(冠点、鞍点、热点)应力弯曲度的计算公式,没有给出沿撑杆-弦杆连接处的应力弯曲度的分布公式。为此,考虑总结各种类型管节点应力弯曲度的计算公式,提出应力弯曲度沿撑杆-弦杆连接处的分布公式,该公式可以考虑位于焊缝任何位置的裂纹。通过将其应用于南海导管架平台管节点裂纹的裂纹扩展分析,以验证其在管节点疲劳裂纹断裂评估中的准确性。
1 弯曲强度折减系数
强度折减系数定义为含裂纹管节点和完好管节点极限强度的比值。BS7190给出的轴向强度折减系数FAR如下。
(1)
式中:Ac为裂纹面积;lw为焊缝长度;T为弦杆壁厚。
基于净截面破坏(NSC)准则,推导弯曲强度折减系数的计算公式。为简化公式的推导,考虑等高度的表面裂纹;断裂力学评估中通常假设裂纹为半椭圆形,半椭圆形表面裂纹可以简化为等效的等高度表面裂纹。由此,裂纹的半角度可以表示为
(2)
式中:φ为裂纹的半角度;c为裂纹的半长度;ro为撑杆的外半径。含等高度表面裂纹的撑杆横剖面见图1。
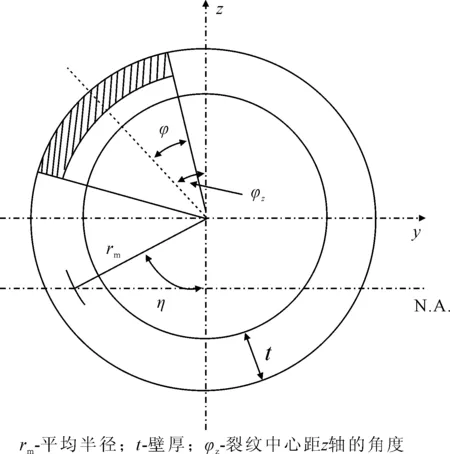
图1 含有等高度表面裂纹的撑杆横剖面
1.1 裂纹全部位于受拉应力区
含裂纹撑杆横截面受平面内弯矩Mi作用,在净截面破坏时的应力分布见图2。图2中的σf为流动应力。假定裂纹全部位于受拉区域,即φ+η≤π-φz。
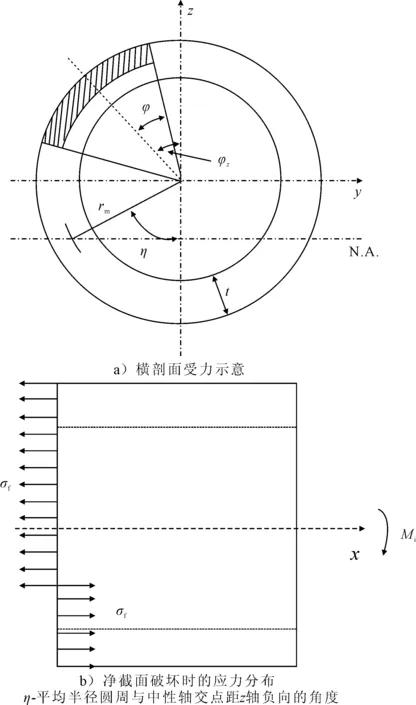
图2 裂纹全部位于受拉应力区的撑杆横剖面受 平面内弯矩作用净截面破坏时的应力分布
根据图2中的轴向力平衡可以得到:
(π-η+π-η-2φ-2η)σf=0
(3)
式中:a为裂纹高度;ri为撑杆的内半径。
由式(3)可以得到塑性中和轴关于z轴的角度η,见图2。
(4)
根据图2中的弯矩平衡可以得到:
(5)
由式(5)可以得到平面内塑性弯矩Mi。
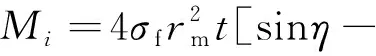
(6)
(7)
同理,含裂纹管节点受面外弯矩作用的弯曲强度折减系数FMRo的计算公式为
(8)
1.2 裂纹部分位于受压应力区
含裂纹撑杆横截面受平面内在弯矩Mi作用下净截面破坏时的应力分布见图3。裂纹部分位于受拉区域,部分位于受压区域,即φ+η>π-φz。
根据图3中的轴向力平衡得到:
(9)
由式(9)得到塑性中和轴关于z轴的角度η。
(10)
根据图3中的弯矩平衡可以得到平面内塑性弯矩Mi。
(11)
含裂纹管节点受面内弯矩作用的弯曲强度折减系数FMRi为
(12)
同理,含裂纹管节点受面外弯矩作用的弯曲强度折减系数FMRo的计算公式为
(13)
2 应力弯曲度
应力弯曲度Ω为
(14)
式中:σb为弯曲应力;σ为总应力。
管节点一般受轴向荷载、平面内弯矩和平面外弯矩的组合作用,应力弯曲度为
(15)
式中:Ωax、Ωipb、Ωopb分别为轴向力、面内弯矩和面外弯矩作用下的应力弯曲度;σax、σipb、σopb分别为轴向应力、面内弯曲应力和面外弯曲应力;SCFax、SCFipb、SCFopb分别为轴向、面内弯曲和面外弯曲的应力集中系数。
API RP2A[17]推荐使用Efthymiou公式计算应力集中系数,但该公式只给出管节点焊缝鞍点和冠点的应力集中系数。若裂纹位于焊缝鞍点和冠点之间,应力集中系数可以采用下面的公式计算。
SCFax=SCFax,crcos2φ+SCFax,sasin2φ
(16)
SCFipb=SCFipb,crcosφ
(17)
SCFopb=SCFopb,sasinφ
(18)
式中:φ为裂纹中心距冠点的角度;SCFax,cr、SCFax,sa分别为冠点、鞍点的轴向应力集中系数;SCFipb,cr为冠点的面内弯曲应力集中系数;SCFopb,sa为鞍点的面外弯曲应力集中系数。
文献[11-16]分别给出不同类型管节点在轴向力、面内弯曲、面外弯曲下的应力弯曲度的经验公式,这些参考文献公式总结见表1。
但是,除文献[12]外,所有文献只给出节点关键位置处(冠点、鞍点)应力弯曲度的计算公式,没有给出沿撑杆-弦杆连接处的应力弯曲度的分布公式。根据相关文献中关于沿撑杆-弦杆连接处的应力、应力集中系数以及弯曲比率分布特点,应力弯曲度可采用下面的分布公式确定。
(19)
Ωipb(φ)=Ωipb,crcosφ
(20)
Ωopb(φ)=Ωopb,sasinφ
(21)
3 管节点裂纹断裂评估推荐做法
断裂评估就是判断管节点裂纹尺寸能否满足“合于使用”要求。管节点裂纹的断裂评估采用失效评定图(FAD)的方法进行,见图4。
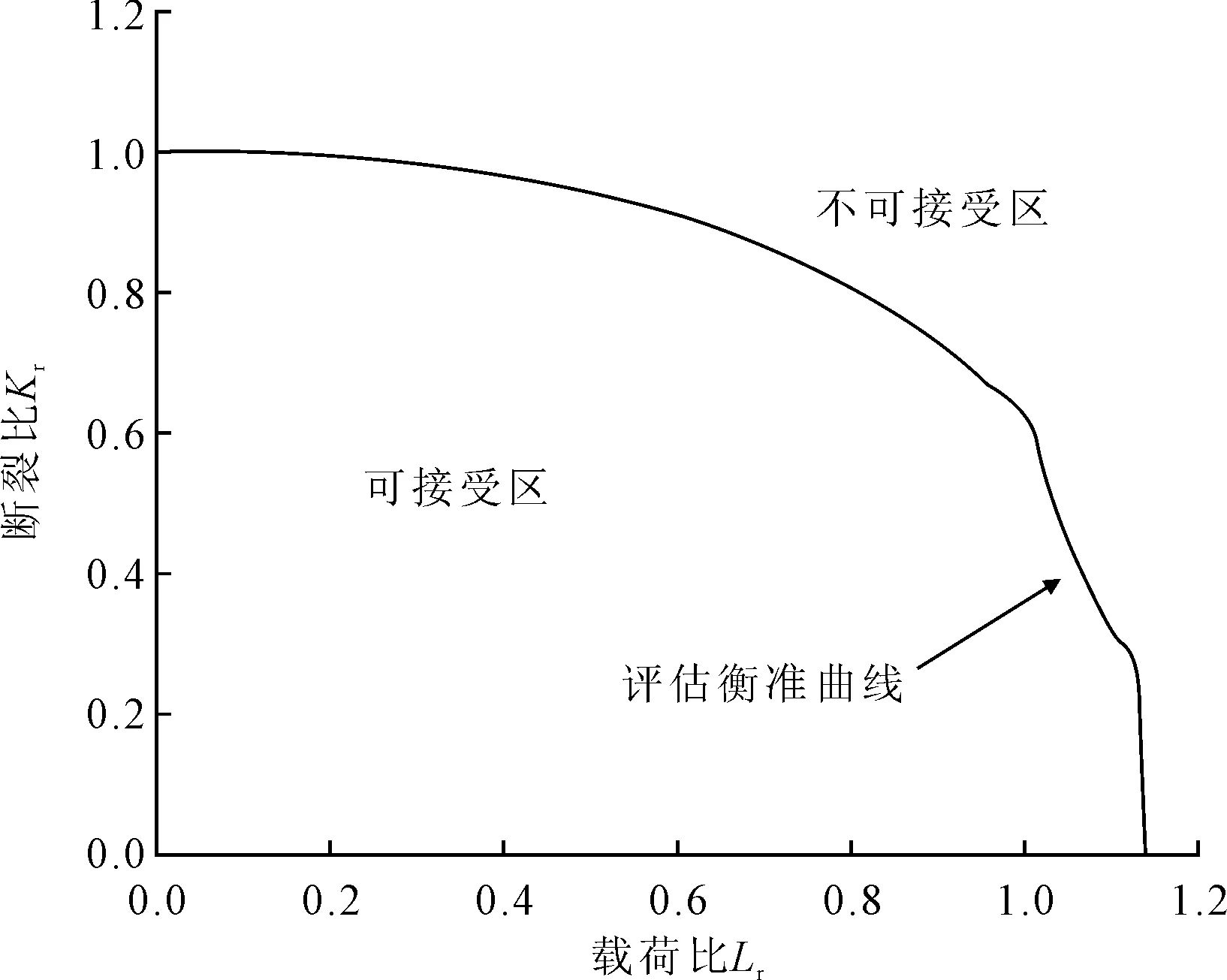
图4 管节点裂纹失效评定图(FAD)
管节点裂纹失效评定曲线采用BS7910的Option 2,根据对应公式可以确定图4的失效评估曲线,计算某一具体缺陷(评估点),得到其坐标值,当评估点位于评估曲线内部时,该缺陷可以接受;当评估点位于评估曲线上或曲线外部时,缺陷不可接受。
断裂比Kr按下面的公式计算。
(22)
式中:Kmat为断裂韧性;Kp、Ks分别为一次应力和二次应力的应力强度因子;V为塑性修正因子。
(23)
式中:Mkm、Mm为膜应力强度因子放大系数;Mkb、Mb为弯曲应力强度因子放大系数;σHS为焊趾处热点应力;a为裂纹深度;Ω为应力弯曲度。
如果是贯通裂纹,应力强度因子为
(24)
荷载比Lr为
(25)
式中:Pa、Mai、Mao分别为轴向力、平面内弯矩和平面外弯矩;Pc、Mci、Mco分别为含裂纹管节点的轴向极限强度、平面内弯曲极限强度和平面外弯曲极限强度;σy为材料屈服强度;σf为流变应力,σf=(σy+σu)/2,σu是材料拉伸极限强度。
含裂纹管节点的极限强度为
(26)
(27)
(28)
式中:T为弦杆壁厚;d为撑杆外径;θ为撑杆与弦杆的夹角;Qu、Qf分别为极限强度系数和弦杆荷载系数,参见API RP 2A 22版。
4 验证和实例
4.1 验证
对弯曲强度折减系数的试验值、有限元分析值与基于式(7)、式(8)、式(12)和式(13)的计算值的比较见图5。
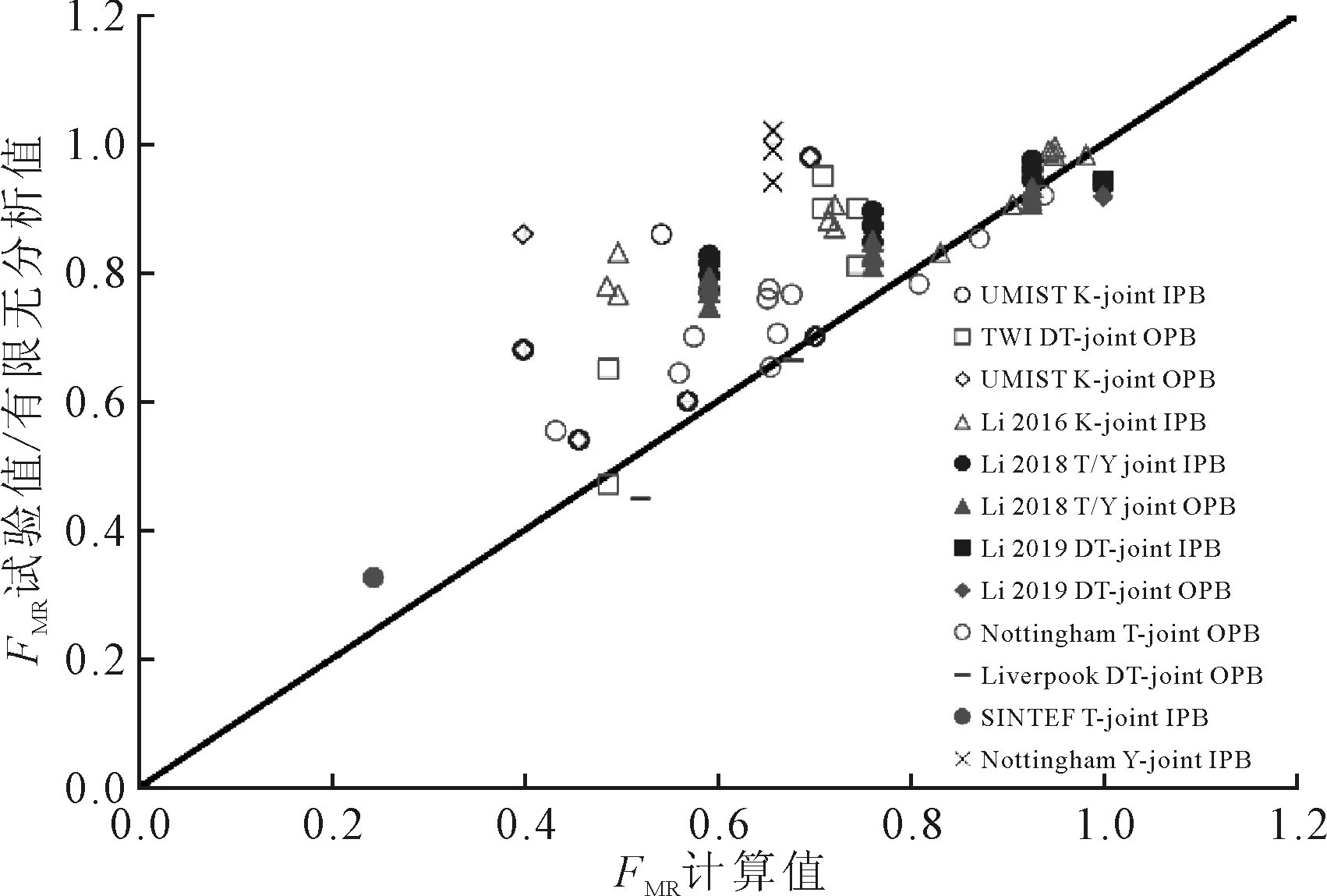
图5 弯曲强度折减系数的试验值/有限元分析值与公式计算值的比较
可以看出,试验数据和有限元分析数据都比较分散,这主要是由试件和有限元模型的几何尺寸和材料差异所引起。与有限元分析不同,试件的失效受到断裂的影响,失效模式不是完全的塑性失效,因此个别试验值小于计算值。但总体趋势:试验值和有限元分析值都大于或接近计算值。以上验证表明,式(7)、式(8)、式(12)和式(13)可以给出偏于安全的弯曲极限强度折减系数的下限值。
4.2 实例
该推荐做法应用于南海某导管架平台的裂纹扩展分析。某导管架在例行检测时发现裂纹,在导管架EL(+)3.8 m水平层节点无损探伤(NDT)时发现54条疲劳裂纹,典型裂纹见图6。以N701-M583裂纹为例进行断裂评估,裂纹初始长为50 mm,深度为6.7 mm。

图6 导管架管节点裂纹群位置图及照片
1)裂纹评估基础数据确定,包括:裂纹类型、尺寸和位置,结构和焊缝的几何形状、尺寸,材料性能数据如屈服强度、抗拉强度、弹性模量、泊松比、应力应变曲线、断裂韧性,管节点处载荷及应力,焊接残余应力。
2)断裂力学方法疲劳分析确定裂纹尺寸随时间的扩展数据,如图7a)所示(该部分内容裂纹评估准备数据,不在此讨论)。
3)选择某时刻裂纹尺寸,利用式(7)、式(8)、式(12)和式(13)计算强度折减系数。
4)利用式(25)~(28)计算载荷比Lr。
5)利用式(16)~(21)计算应力集中系数和应力弯曲度。
6)利用式(22)~(23)计算应力强度因子和断裂比Kr。
7)画管节点裂纹失效评定图,绘出点(Lr,Kr)。
8)选取另一时刻裂纹尺寸,重复步骤3)~7)。
9)评定整个服役期间的裂纹是否可以接受。
图7b)是位于管节点N701和撑杆M583环焊缝的一个弦杆焊趾裂纹的失效评估图(FAD)。结构探伤已确定裂纹深度,管节点裂纹扩展分析结果表明,裂纹可以接受,计算的剩余疲劳寿命是32年。
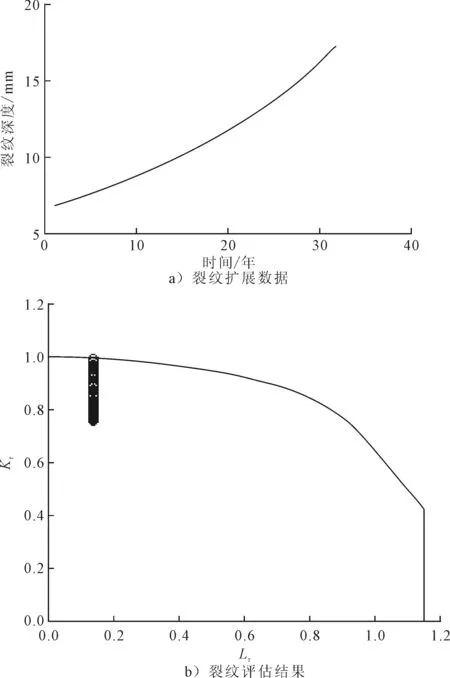
图7 N701-M583裂纹(50 mm×6.7 mm)失效评估
5 结论
1)改进的BS7910关于导管架管节点的裂纹失效评估方法适用于各种类型管节点环焊缝任何位置的裂纹评估和载荷评估,改进的裂纹失效评估方法已应用于南海导管架管节点疲劳裂纹评估分析。
2)基于净截面失效(NSC)准则,提出了含裂纹管节点平面内和平面外弯曲强度折减系数的封闭形式解析解和含裂纹管节点的极限强度计算方法,该公式的适用性与已有的试验数据和有限元分析结果比较并得到了验证。
3)提出了各种类型管节点的应力弯曲度沿撑杆-弦杆连接环焊缝处的分布公式。
4)循环应力范围时历曲线对裂纹扩展起到重要作用,下一步将对管节点裂纹处循环应力范围时历曲线进行更多研究,提出适合工程实践的准确方法。
