基于参数辨识的推进电机模型参考自适应控制
2023-04-27吕长龙周毅李萌蒙学昊罗文忠
吕长龙,周毅,李萌,蒙学昊,罗文忠
(中海油能源发展股份有限公司采油服务分公司,天津 300452)
对于永磁同步电机(PMSM)无传感器控制系统,准确估计电机转速和转子位置是控制系统实施的主要任务。目前研究和应用最广泛的方法主要有开环磁链法、观测器法、模型参考自适应系统(MRAS)、旋转/脉冲高频注入法、神经网络等[1-2]。MRAS在PMSM无传感器控制系统中的应用是通过电流传感器测量电机定子电流实际值与数学模型计算出的估计值之间的误差,设计自适应率,进而估计出电机的转子位置信息。这种方法由于物理意义明确、设计相对简单、识别准确率高而被广泛使用[3]。
为保证PMSM无传感器控制系统对电机转速具有较高的估测精度,控制系统中的电机参数必须足够精确。在实际应用中,电机参数会随电机运行状态,环境温度等发生改变。因此控制系统必须具有电机参数实时在线修正的能力。在基于MRAS的PMSM无传感器控制系统中,MRAS的实现离不开电机模型中准确的电机参数。电机定子电阻和电感随温度而变化,从而降低了估计转子位置信息方法的准确性。针对这一问题,提出使用参数辨识实时修正控制系统中模型参数的设计方案。利用计算速度快,结构简单的Adaline神经网络对电机参数进行参数辨识,将辨识值反馈至MRAS中,实时修正MRAS中的模型参数,提高MRAS对电机转速和转子位置角的估测精度,提升推进电机的控制性能。
1 PMSM矢量控制
1.1 PMSM数学模型
PMSM在dq坐标系下的等效电路见图1[4]。
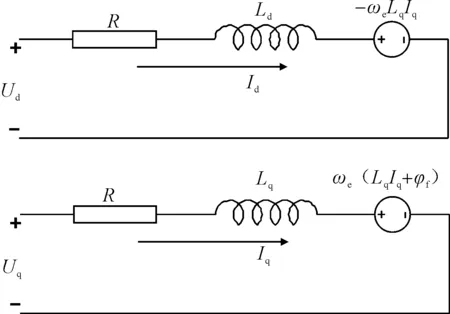
图1 PMSM在dq坐标系下的等效电路
则PMSM在dq轴的等效电路电压方程为
(1)
式中:Id、Iq是dq坐标系下的定子电流;Ud、Uq是dq坐标系下的定子电压;R是定子电感;Ld、Lq是dq轴的电感;ωe为转子电气角速度;φf为转子磁链。
电机的电磁转矩方程为
(2)
式中:pn为电机磁极对数。
此时,电机的运动方程为
(3)
式中:TL为电机负载转矩。
根据公式(2)和(3)可知,在dq坐标系中,电磁转矩与机械角速度成正比,而在(3)中,电磁转矩又与q轴电流成正比。因此在PMSM的控制系统中,可以通过对q轴电流的控制,实现对电机转速的控制,因此选择id=0的矢量控制。
1.2 基于id=0矢量PMSM矢量控制系统的实现
PMSM矢量控制系统组成见图2[5]。

图2 PMSM矢量控制系统组成
图中,ia、ib、ic是三相定子电流;id、iq是dq坐标系下的定子电流;θe是电气角度;ωe是电机实际电气角速度。PMSM矢量控制是一个由电流控制环和速度控制环组成的双闭环控制系统。速度控制环的输入由电机转子给定机械角速度ωmc和电机转子实际机械角速度ωm构成,两者做差后经速度控制器,输出为电流控制环q轴电流的输入量iqc。电流控制环的输入由给定的d轴电流idc=0和q轴电流iqc构成,将给定的d轴电流与反馈得到的d轴电流id做差,经d轴电流控制器输出d轴控制电压Vcond;将q轴电流iqc与反馈得到的q轴电流iq做差,经q轴电流控制器输出q轴控制电压Vconq。之后两相控制电压经电压空间矢量脉宽调制(SVPWM)生成功率开关管的控制信号,从而实现PMSM的速度控制。
2 无传感器控制系统的设计
2.1 模型参考自适应系统
MRAS的结构图见图3,其基本思路是以参数未知的数学表达式为参考模型,参数未知的表达式为可调模型。两种模型的输出物理意义相同。通过使用两个模型的输出值之间的误差来估计转子速度和转子位置来设计参数适应率[6]。

图3 MRAS系统结构
在图3中,u是系统的输入,Ym和Yn是期望模型和可调模型输出的状态量,e是Ym和Yn之间的误差。
根据PMSM在dq轴上的电压方程得到电流方程为
(4)
为了获得PMSM的可调模型,将公式(4)重写为
(5)
式中:
(6)
将公式(5)改写为:
(7)
将输出误差定义为e=I-I′,则误差方程为
(8)
其中:
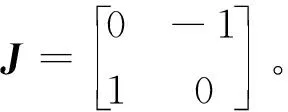
为保证控制系统稳定,根据Popov超稳定性判据,须满足以下条件。
1)传递函数H(s)=(sI-Ae)-1为严格正定矩阵。

根据Popov积分不等式可得电角速度的自适应律为
(9)
将式(6)代入式(9),可得
(10)
则估测得到的转子位置角为
(11)
2.2 Adaline神经网络在线参数辨识
Adaline神经网络结构见图4,图中X1、X2、…、Xn为网络输入,W1、W2、…、Wn为网络各输入量对应的权值,O(k)为神经网络的实际输出,d(k)为目标输出,k代表第k次采样[7]。
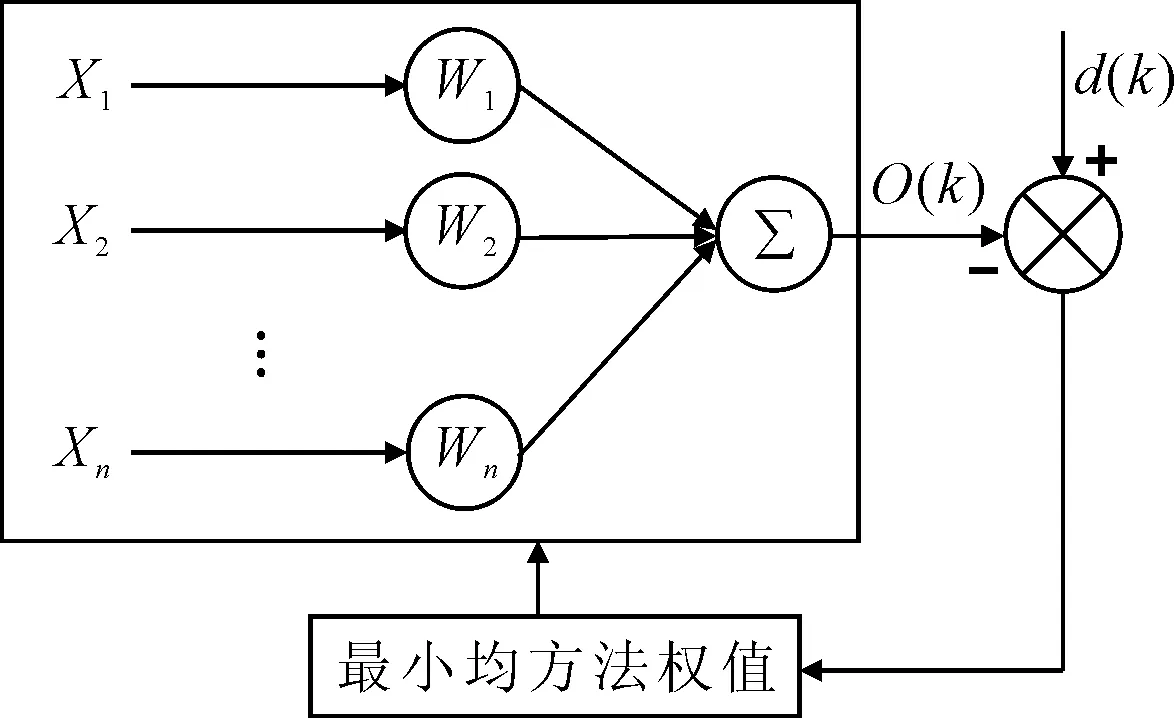
图4 Adaline神经网络系统框图
此时网络输入矢量为
X=[X1,X2,…,Xn]T
(12)
权重矢量为
W=[W1,W2,…,Wn]T
(13)
X和W之间的函数关系可以表示为
(14)
式中i=1,2,3,…,n。
根据最小均方误差法调整网络权重,通过最速下降法可以得到
ΔW=2η·[d(k)-O(k)]·X(k)
(15)
η是一个大于0的有界正数。通过使网络权重适应最小均方误差法,可以得到
(16)
式中:X(k)、O(k)、W(k)和d(k)分别为Adaline神经网络在第k次采样时的输入、输出、权重和目标输出;ε(k)是O(k)和d(k)之间的误差信号;λ是权重计算的步长。
在使用Adaline神经网络对PMSM进行在线参数识别时,λ需要满足下式,以保证Adaline神经网络的收敛性。
0<2λ|X(k)|2<1
(17)
根据id=0矢量控制策略,PMSM的参数辨识模型为
(18)
由于(18)中电压方程的秩为2,Ls,R和φf不能同时识别。故采用注入d轴电流法来解决这一问题[8]。此时,Ls,R和φf的全秩辨识模型为
(19)

那么,PMSM的参数自适应率为
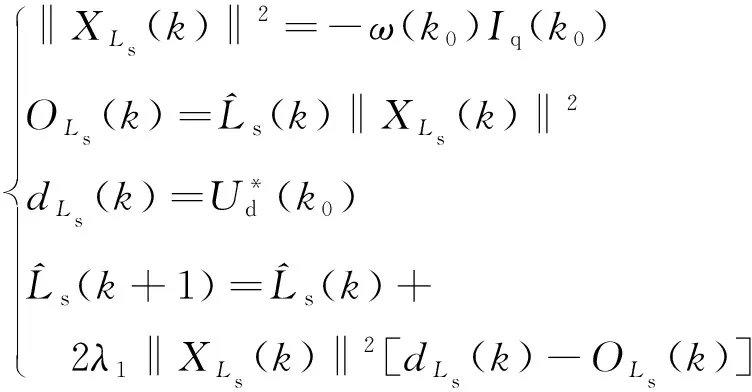
(20)
(21)
(22)
式中:XL(k)、XR(k)、Xφf(k)为各参数辨识模型的输入;OL(k)、OR(k)、Oφf(k)为各参数辨识模型的输出;dL(k)、dR(k)、dφf(k)为各参数辨识模型的目标输出。根据公式(20)、(21)、(22)即可对PMSM的Ls、R和φf进行参数辨识。
3 控制系统仿真
3.1 基于SVPWM的PMSM矢量控制
根据图1搭建基于id=0的PMSM矢量控制仿真模型。仿真模型选用某船用PMSM的主要参数见表1。
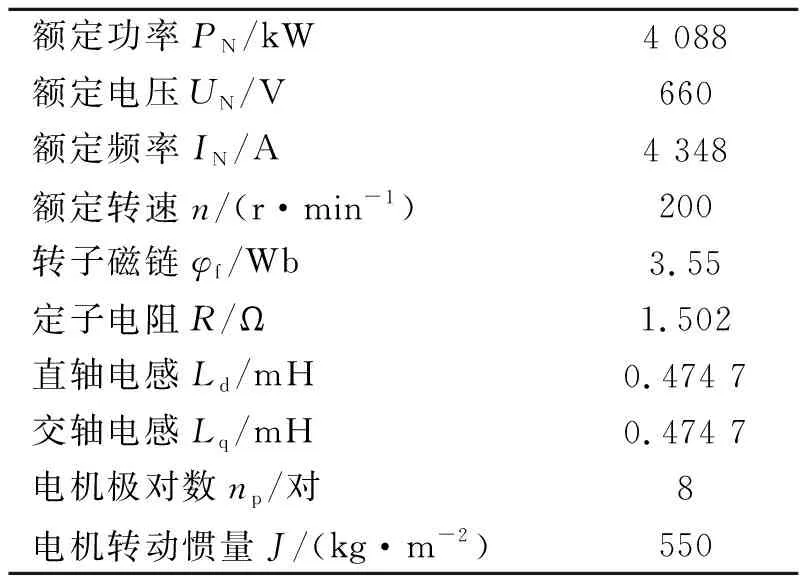
表1 PMSM主要参数
仿真过程中,设定电机起动时负载转矩为100 000 N·m,给定转速为150 r/min,0.5 s时转速突变为200 r/min,仿真时间为1 s。仿真得到的电机转速、转子位置和三相定子电流见图5。

图5 基于SVPWM的PMSM矢量控制仿真结果
分析转速波形图可知,转速变化过程中无超调量,转速变化速度快且平滑。在电机运行过程中,定子电流随转速的变化而发生响应变化。从仿真结果可知,该控制系统在转速发生变化时,响应速度快,曲线平滑,证明该系统具有很好的动、静态性能。
3.2 基于MRAS的PMSM无传感器控制
根据图6搭建基于MRAS的PMSM无传感器控制仿真模型。
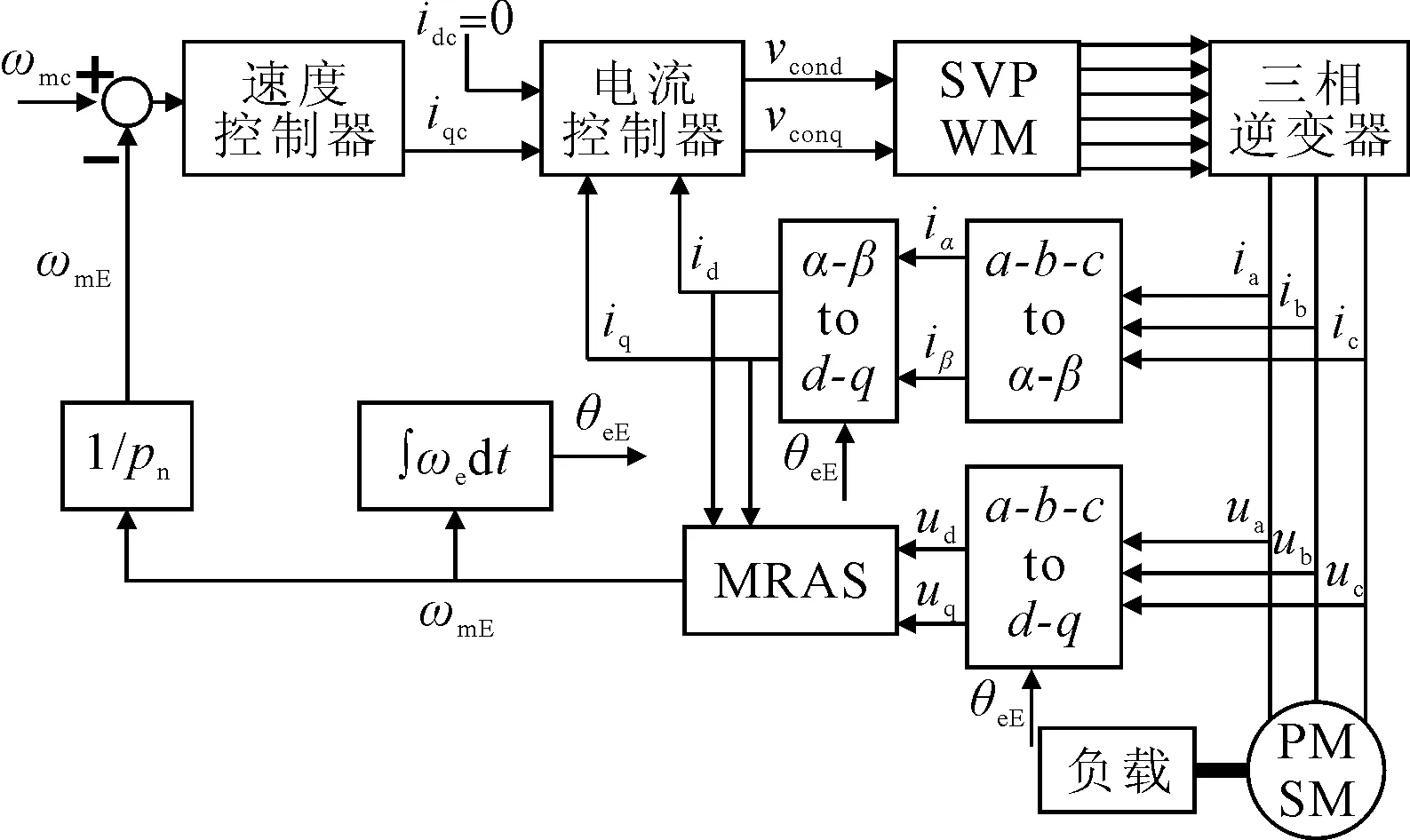
图6 基于MRAS的PMSM无传感器控制系统图
仿真过程中,按照上节仿真过程进行仿真实验。电机转速、转速估测误差和转子位置角估测误差的仿真结果见图7。

图7 基于MRAS的PMSM无传感器控制仿真结果
由图7可知,使用MRAS估测电机转速和转子位置时,在电机稳定运行时对转子转速的估测误差约为9 r/min,转子位置角的估测误差约为0.12 rad。在转速突变时,MRAS对转速的估测误差增大。总体分析可知,基于MRAS的PMSM无传感器控制仿真模型对转子转速和转子位置具有较好的估测性能,但对电机转速的估测精度需进一步提高。
3.3 基于参数辨识的PMSM模型参考自适应控制
根据图8在Simulink中搭建基于参数辨识的PMSM模型参考自适应控制系统仿真模型。控制系统包含SVPWM控制模块,MRAS模块和Adaline神经网络参数辨识模块等。在控制系统中ud、uq、id、iq作为MRAS的输入,ωeE是MRAS输出值。ud、uq、id、iq为Adaline神经网络的输入量,经Adaline神经网络模块,测量出电机运行时的电机参数。利用该辨识值修正无传感器控制系统中的模型参数,按照上节仿真过程进行仿真实验,得到的仿真结果见图9。
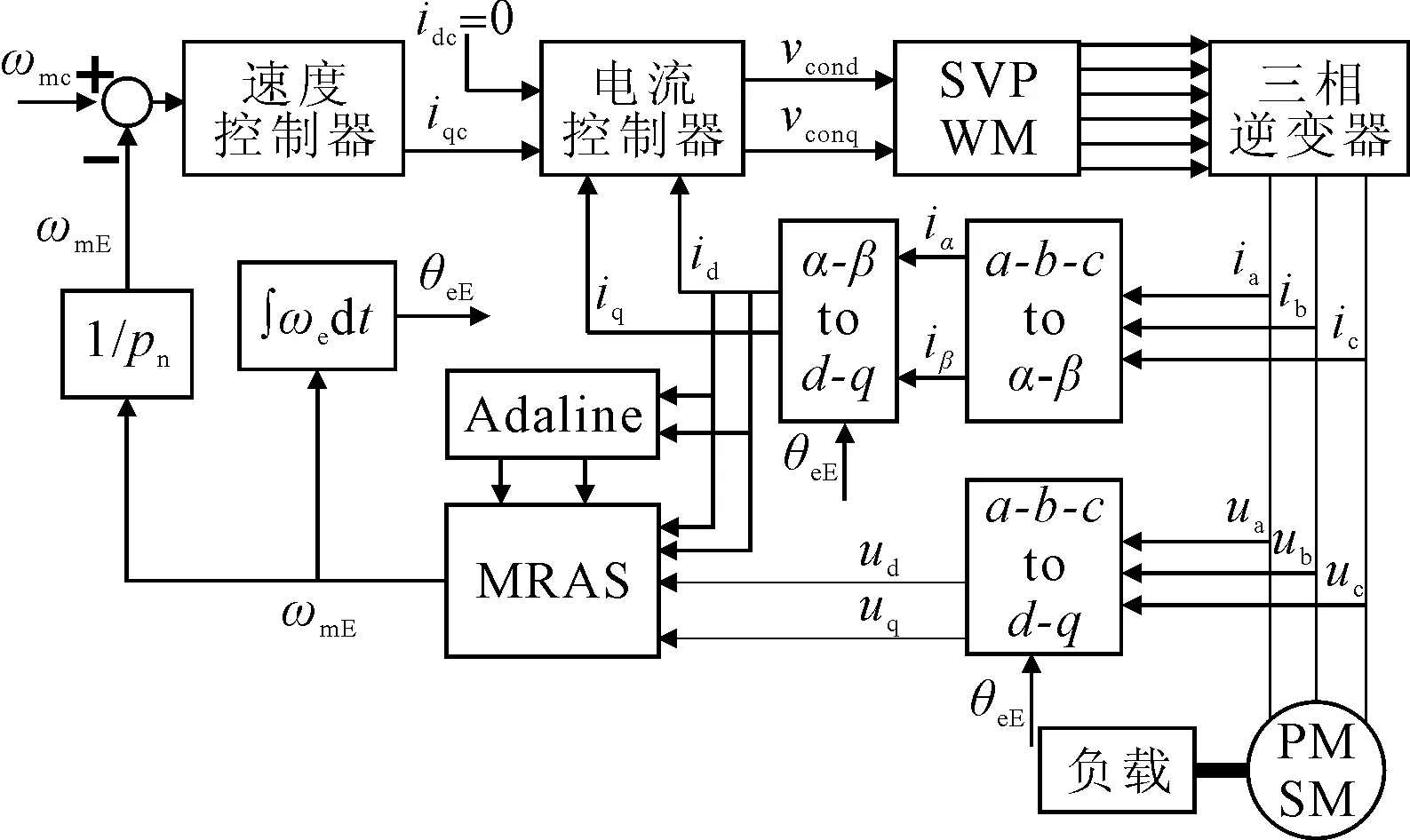
图8 基于参数辨识的PMSM模型参考自适应控制系统图

图9 基于参数辨识的PMSM模型参考自适应控制仿真结果
由图9可知,当转速变化时,使用Adaline神经网络对模型参数进行修正,可有效提高MRAS对转子转速和转子位置的估测精度。同时通过对转速变化曲线的分析,基于参数辨识的PMSM模型参考自适应控制系统使转速更加平滑。
仿真过程中电机定子电阻、电感和转子磁链的参数辨识见图10。

图10 参数辨识曲线
由图10可知使用Adaline神经网络参数辨识在电机稳定运行时响应速度快,检测精度高,可以很好地检测电机运行时的状态参数,满足该控制系统的设计要求。
4 结论
在船舶推进电机的控制系统中,使用MRAS估测电机转速摆脱了对机械传感器的依赖,可提高船舶航行的安全性。使用Adaline神经网络实时修正MRAS中的模型参数,可提高MRAS对电机转速的估测精度。通过利用Simulink进行仿真验证,结果表明,基于参数辨识的PMSM模型参考自适应控制系统提高了对电机转速的估测精度,并保持控制系统具有很好的抗干扰能力。面对船舶智能化的发展趋势,船舶推进电机的无传感器控制需进一步提高电机转速的估测精度。
