穿梭油轮外输工况系船缆张力影响分析

韩宇,钟启源,李英

(1.中海油能源发展股份有限公司采油服务分公司,天津300452;2.天津大学 建筑工程学院,天津 300072)

采用穿梭油轮外输作业时,FPSO与穿梭油轮靠泊方式分为并靠和串靠,串靠外输作业过程涉及多浮体的耦合运动,并且受风、浪、流等多种环境参数及多种装载工况影响,针对FPSO外输工况,国内外的研究主要集中在建立多体数值模型开展耦合时域模拟,将模拟结果与力学模型或试验模型结果相比较,验证可靠性,并且重点关注系泊缆索的张力变化[1-10]。本文主要针对FPSO串靠外输工况下的系船缆张力,开展多种工况条件下的多浮体时域耦合分析,获取系船缆张力时历变化,分析多参数对系船缆张力变化的影响,保障外输作业安全进行。

1 计算理论

1.1 一阶波浪力

浮体在水中运动时会受到波浪力的作用,一般情况下波浪力包括浮体强迫振动产生的辐射力、浮体固定时入射波浪产生的入射力、浮体固定时产生的绕射力以及静水力载荷,对于FPSO这种大尺度结构物而言,一阶波浪力主要包括未扰动入射波的波压强对浮体产生的Froude-Krylov力和扰动波压强对浮体产生的绕动力。

采用线性伯努利方程计算浮体表面的波压强,将散射波速度势与入射波速度势线性叠加,得到波动场内任意一点总速度势,求出浮体表面S各点的波压强,公式如下:

ωρRez[i(φI+φS)e-iωt]

(1)

沿着浮体静水湿表面积分得到浮体受力:

(2)

求得一阶波浪力为

(3)

式中:φI(x,y,z,t)为入射波速度势;φS(x,y,z,t)为散射波速度势;ω为波浪圆频率;ρ为海水密度。

1.2 二阶波浪力

浮体在水中运动既会受到一阶波浪力,也受到二阶波浪力的影响,二阶波浪力主要包括波浪平均漂移力、低频波浪力和高频波浪力。对于FPSO和穿梭油轮,二阶波浪力主要是平均漂移力和低频波浪力。低频波浪力由一阶波场的二次积和入射波和绕射波的二阶速度势组成,严重影响海上平台的正常作业。求解二阶低频载荷常采用Newman近似法,对于M个波浪单元,低频载荷为

(4)

Newman近似法求解较为简便,精度可以满足工程上一般要求。

2 外输作业多体耦合分析模型

2.1 模型参数

FPSO、系船缆、钢臂系泊系统及穿梭油轮主要参数见表1。

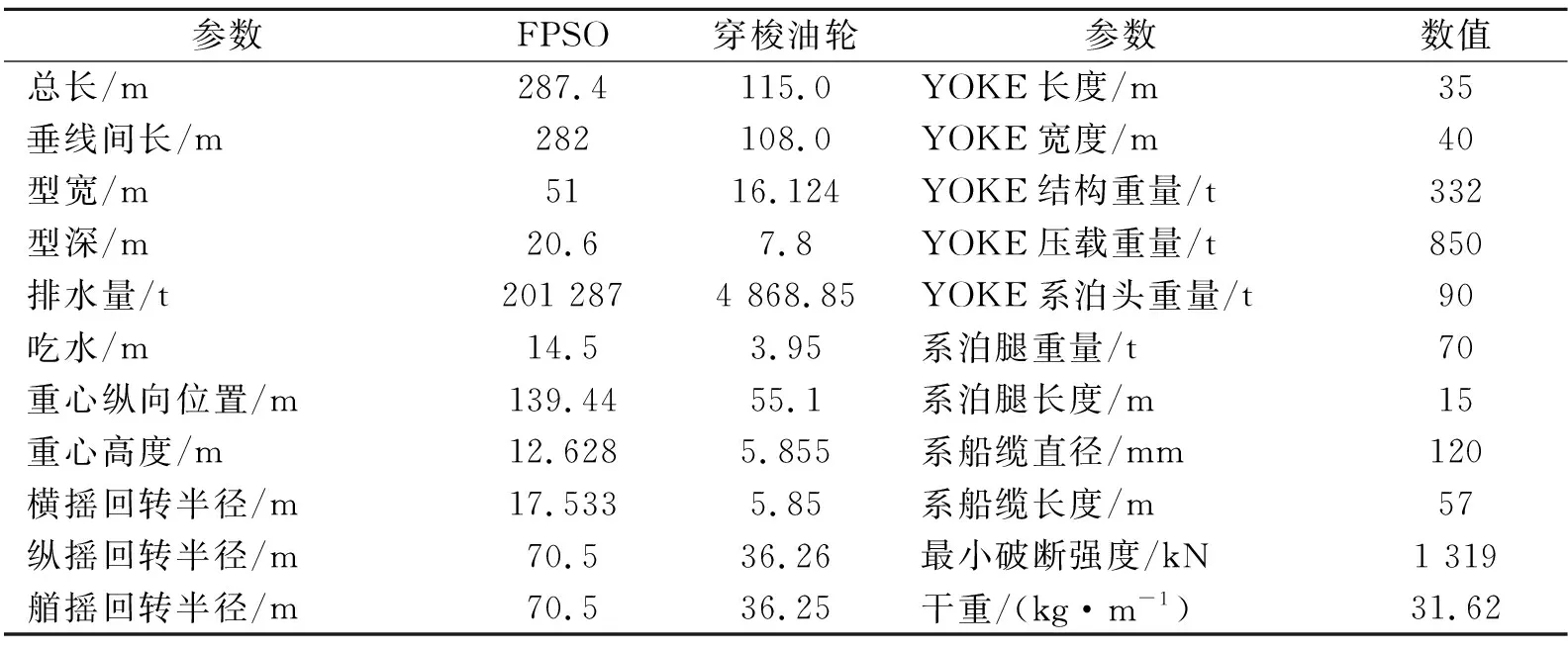
表1 时域模型主要参数

设定船体坐标系原点位于船体重心处,x轴由船尾指向船艏,y轴由右舷指向左舷,z轴由船底指向甲板,穿梭油轮与FPSO船体坐标系定义保持一致。在OrcaFlex中建立软钢臂系泊系统、FPSO、系船缆与穿梭油轮多浮体模型见图1。FPSO在渤海海域作业,海洋环境条件见表2。图1给出了应用AQWA 开展水动力分析的FPSO一阶水动力响应RAO。

表2 作业海域环境条件

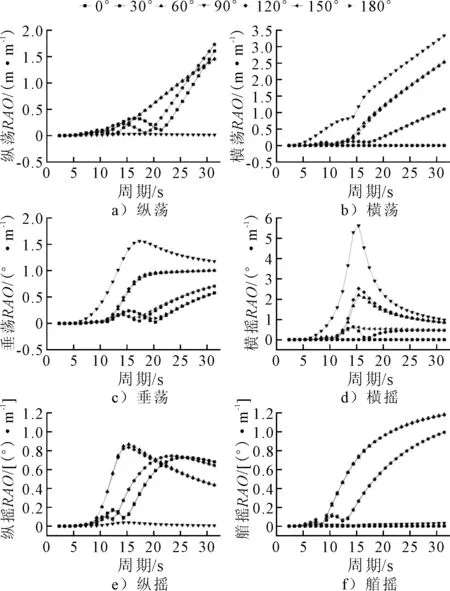
图1 FPSO满载工况六个自由度RAO

2.2 时域分析

开展外输工况下的多浮体时域分析时,考虑风浪流载荷的联合作用,依照作业海域海况以及规范要求,组合计算工况,并依据OCIMF规范计算船体所受风、流载荷。

根据ABS规范[11],对风浪流角度按照以下方式进行组合。考虑多浮体系统具有对称性,环境载荷作用方向在0～180°范围内按照15°间隔作用在浮体上。风浪流不同向时,风与波浪方向相差30°,流与波浪方向相差90°。组合工况见表3。

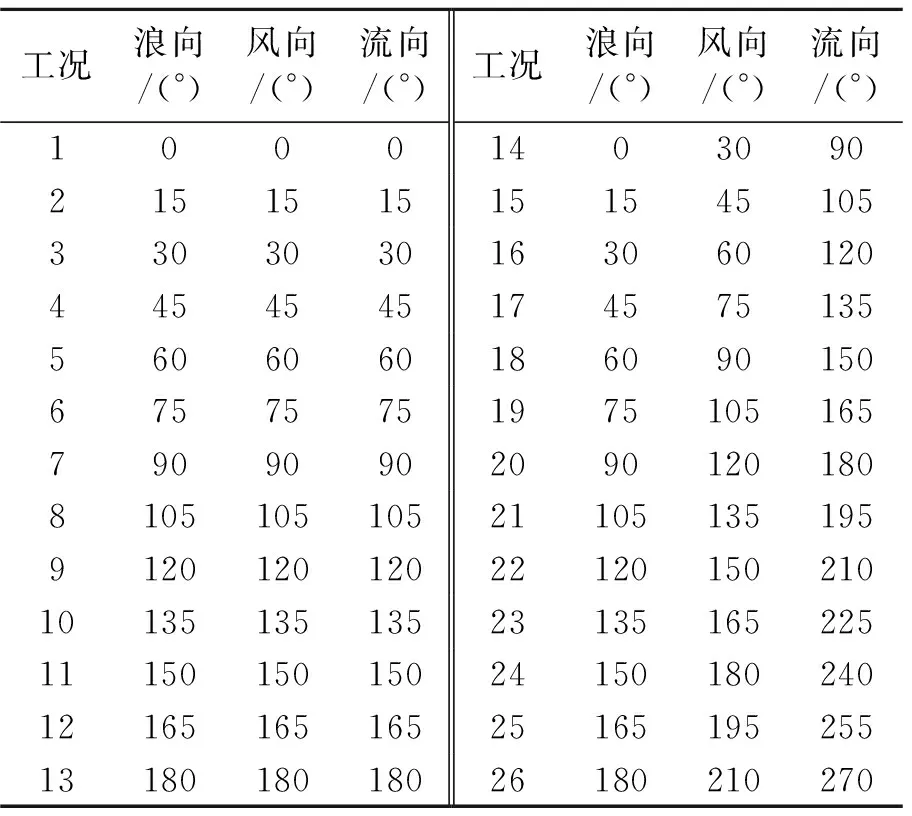
表3 时域耦合分析工况

本文动力计算方法选取隐式时域计算,一般短期海况是3 h,考虑到计算时间及工作量,在对比了1 h和3 h模拟结果的基础上,本文时域模拟时长设置为1 h。

2.3 结果分析

2.3.1 系船缆最大张力

依据规范API RP 2SK[12]要求,在进行浮体响应分析时,系泊缆的安全系数应不小于1.67。本文系船缆的破断张力为1 319 kN,经计算,所涉及的全部工况,系船缆校核后都符合规范要求,所有工况中安全系数最小值也大于2,超过规范要求的安全系数,说明各工况下系船缆的张力均处于较为安全的水平。

风浪流联合入射的角度从0°～180°,系船缆张力最大值呈现出先增大后减小的规律,在45°和135°附近达到最大值,在90°时,系船缆张力达到最小值,见图2。

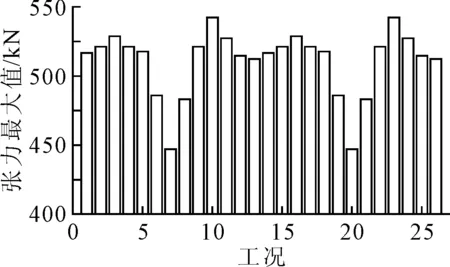
图2 外输工况系船缆最大值

以工况1和14为例,两种工况的区别主要是风与流的作用方向,波浪作用方向一致,这可以说明在风浪流联合作用于多浮体系统时,波浪载荷起主导作用。

2.3.2 FPSO与外输油轮最小间距

FPSO外输作业时其与穿梭油轮串靠在一起,而穿梭油轮没有系泊,为了保证作业时FPSO与穿梭油轮不发生碰撞,重点分析二者之间的最小间距。实际工程中常常在穿梭油轮尾部使用一艘拖轮施加拉力以减小穿梭油轮运动响应,本文中未考虑拖轮。通过提取一年一遇风浪流同向工况下系船缆两端位置时历变化,计算得出FPSO与穿梭油轮之间间距最小值,见图3。

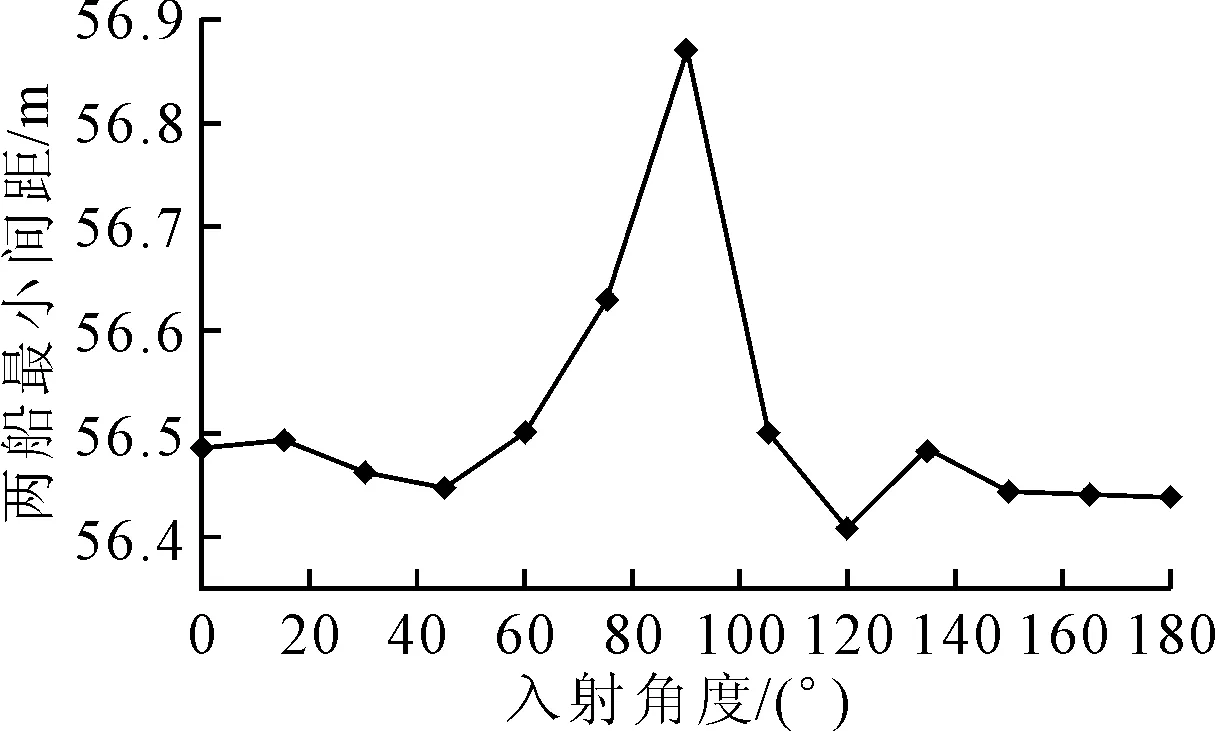
图3 FPSO与穿梭油轮间距最小值变化

图3表明,FPSO与穿梭油轮间距的最小值整体上呈现随着风浪流入射角度先增大后减小的趋势,在入射角度为90°达到最大。这是由于在风浪流横向入射时,船体纵荡方向RAO较小,所以两船体间距较大。两船体间距变化总体上较为稳定,在外输工况中的最小值也大于56 m,处于较为安全的距离,可以保证安全开展外输。

3 系船缆张力敏感性分析

3.1 有效波高的影响

本文外输作业海域为渤海,一年一遇操作工况的有效波高为2.5 m,另外,在实际工程中也往往选择海况较好的天气进行外输作业,有效波高都不会大于2.5 m。因此本文针对波浪有效波高为0.5、1.0、1.5、2.0和2.5 m,分析风、流载荷不变的情况下波高对系船缆张力的影响,见图4。

图4表明,系船缆张力的最大值和平均值随有效波高的增大而增大,并且系船缆张力的均方差也随之增大,说明张力随时间变化更加剧烈,但是在风浪流90°即横向入射时,三者的变化较小,这主要是由于横向浪对纵向张力的影响较小,有效波高增加的影响不够明显。

3.2 波周期的影响

在一年一遇风浪流同向入射的工况下,保持有效波高2.5 m不变,改变谱峰周期为5、6、7 s,分别开展时域耦合模拟,与谱峰周期8 s的原工况进行对比,分析多种海况下的多浮体耦合系统响应,见图5。

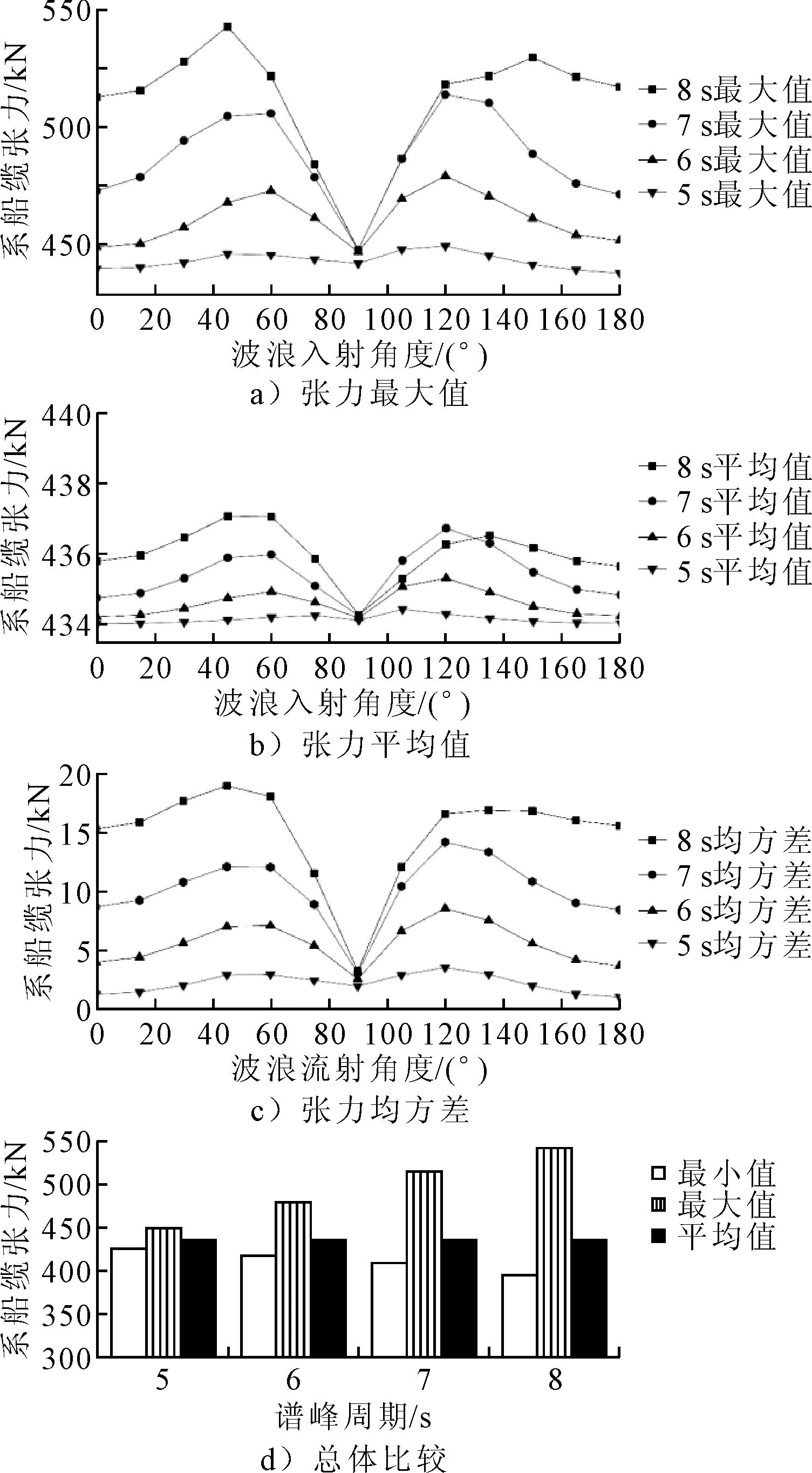
图5 不同谱峰周期系船缆张力变化

图5表明在本文选取的谱峰周期内,整体上系船缆张力的最大值与平均值随着谱峰周期的增大而增大,最大值的增大幅度要大于平均值的增大幅度。在入射角度为105°和120°时,谱峰周期7 s的系船缆张力平均值大于周期为8 s,并且最大值十分接近,说明系船缆张力与谱峰周期存在着一定的非线性关系。

3.3 系船缆长度的影响

系船缆的长度在外输工况中同样会影响张力的时历变化,保持其他条件不变的情况下,分别计算系船缆长度为50、60、70和80 m情况下的系船缆张力变化。

图6表明,系船缆张力的最大值与平均值随着系船缆长度的增大而增大,增大程度较为明显,可以呈现出较为显著的分层,并且随着载荷入射角度的变化,张力最大值的变化趋势是一致的,即从0°～90°先增大后减小,在90°时达到最小值,从90°～180°先增大后减小,整体上的极值出现在45°和135°附近。张力的均方差随着系船缆长度的增加,有一定程度的减小,说明随着系船缆长度的增大,张力的变化剧烈程度减弱,趋于稳定,整体的外输工况也较为安全。

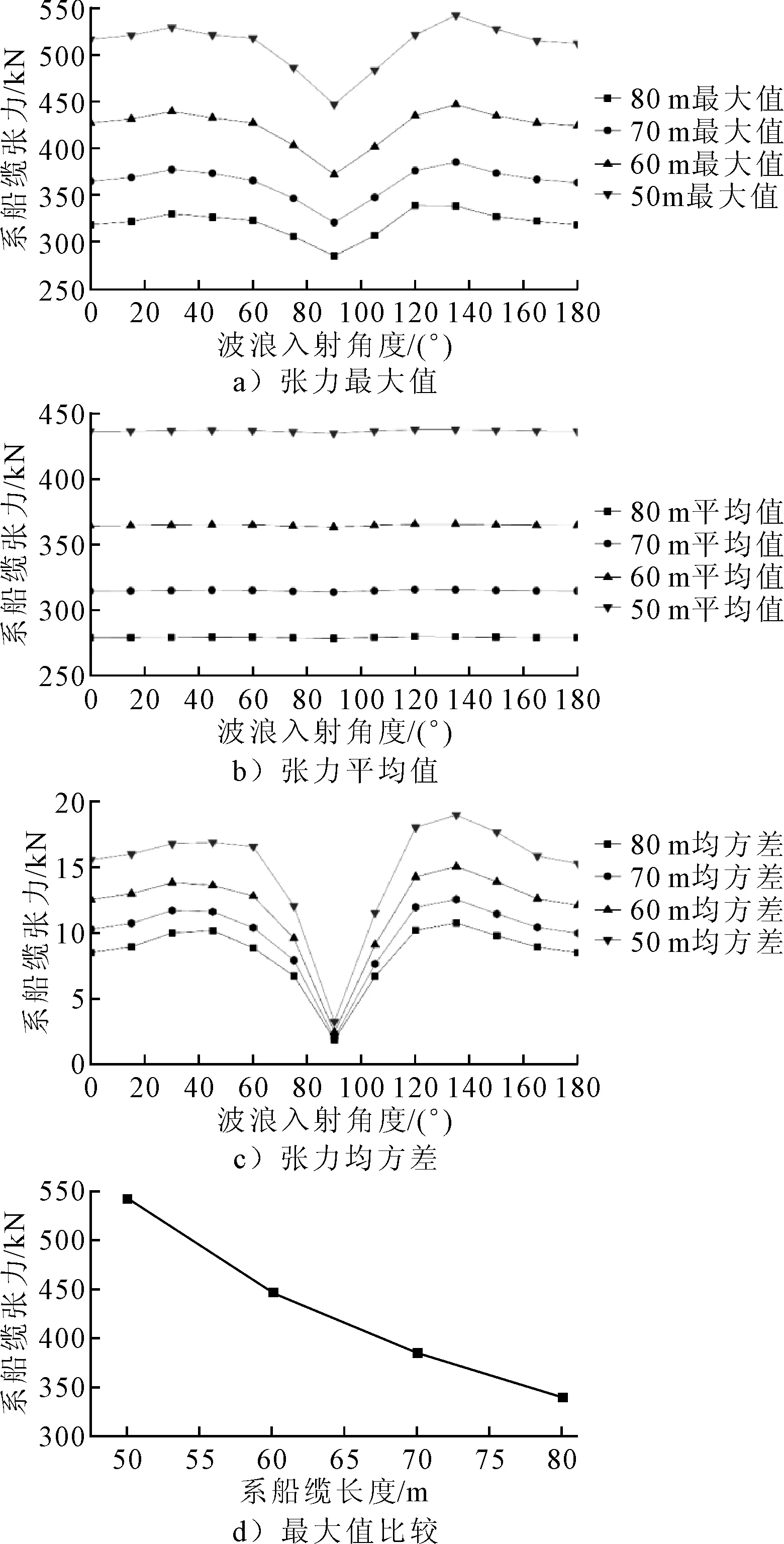
图6 不同系船缆长度张力变化

虽然增大系船缆长度会减小系船缆张力的最大值,但是在50 m的长度下,张力最大值的安全系数大于2.0,已经处于一个较为安全的情况,增大系船缆的长度虽然有助于外输工况的安全开展,但也会增加项目所需的资金,经济性较差,具体系船缆长度的选取需要结合项目的多方面综合考虑。

4 结论

1)外输作业时风浪流联合入射角度对系船缆张力的影响,从0°～180°时,张力呈现先增大后减小的趋势,系船缆张力的峰值集中在入射角度45°和135°附近,当风浪流90°入射时,整体张力水平最小。

2)有效波高从0.5～2.5 m变化时,系船缆张力的整体水平增大,张力的均方差出现明显增大,说明张力水平随时间变化更剧烈,浮体的运动响应也随之增大。

3)波浪谱峰周期从5 s增加到8 s时,系船缆张力整体呈现增大的趋势,但是在部分工况下,出现系船缆张力减小的情况,说明谱峰周期与系船缆张力呈现一定的非线性影响,主要是与FPSO和穿梭油轮的RAO相关。

4)当系船缆长度变化时,会对外输工况中的系船缆张力产生较大影响,从50 m增加至80 m时,系船缆张力最大值与平均值均出现明显减小,需要结合现场施工条件、船体运动响应、经济条件等多方面因素确定合适的系船缆长度。