思想引领,能力提升——函数与导数的综合问题

■江苏省常州市金坛第一中学 宫鸡明

导数及其应用是数学史上的一个重要转折,由此数学发展到了变量数学的新阶段,开辟了数学研究的崭新天地,是一个具有划时代意义的里程碑。导数不仅为有效解决初等数学问题提供了一般性的方法,而且激活了高中数学的各种知识应用及其关系,如求曲线方程、函数的单调区间、函数的最值等,而且涉及了高中数学中很多重要的数学思想方法。

一、函数与方程思想

函数与方程思想就是回归问题的函数或方程本质,利用函数(或方程)知识或函数(或方程)观点来观察、分析与处理问题。函数与方程思想在导数及其应用中主要用来解决生活中的优化问题,以及构造函数证明等式或不等式等。

例1(2023 年江苏省百校联考高三数学试题)已知函数f(x)=2ex-1-a(xlnx-1)-2x,x∈(1,+∞)。

(1)当a=0时,求曲线y=f(x)在x=2处的切线方程;

(2)若f(x)>0,求实数a的取值范围。

解析:(1)当a=0时,函数f(x)=2ex-1-2x,求导可得f′(x)=2ex-1-2,结合导数的几何意义可得k=f′(2)=2e-2,而切点为(2,2e-4),故所求切线方程为y=(2e-2)(x-2)+2e-4,即y=(2e-2)x-2e。

点评:借助不等式恒成立来确定相关参数的取值范围时,关键就是利用参数分离法分离参数,借助函数与方程思想,引入新函数,利用导数及其应用求得新函数的最值或取值范围,综合函数与不等式的相关性质,从而求得参数的范围。

二、分类讨论思想

分类讨论思想就是当我们面临的数学问题不能以统一形式解决,或因为一种形式无法进行概括时,往往可以采用分类讨论思想解决相关问题。分类讨论思想在导数及其应用中主要用来求解单调区间、参数范围、极值、最值及恒成立等问题。

点评:在不同的参数取值情况下对应的函数的极值点的个数也不相同,这时不需要通过参数的取值情况加以分类讨论,而是在不同条件下加以分析与讨论。分类讨论思想在解决一些含参的函数与导数应用问题中,往往是离不开的一种基本数学思想方法。

三、数形结合思想

数形结合思想就是实现“数”与“形”之间的等价转化,或给抽象的数量关系赋予形象和直观的几何意义,或用数量关系描述直观的几何性质等。数形结合思想在导数及其应用中主要用来解决有关方程的根的问题等。

例3(2023 年浙江省名校协作体高三数学试卷)已知函数f(x)=(2a-x)lnx,a>0。

(1)当a=e时,求f(2e-x)的单调区间。

(2)设函数g(x)=f(2a-x)-f(x)。

①若g(x)有且只有一个零点,求实数a的取值范围;

②记函数h(x)=若关于x的方程h(x)=2lna-2 有4 个根,从小到大依次为x1,x2,x3,x4,求证:x3-x2>2;x4-x1<

解析:(1)令f(2e-x)=xln(2e-x)=p(x),x∈(-∞,2e),则p′(x)=ln(2e-x)因为p′(x)在定义域上是单调递减的,且p′(e)=0,所以当x>e时,p′(x)<0;当x0。所以x=e 为p(x)的极大值点,所以f(2e-x)在(0,2e)上单调递增,在(e,2e)上单调递减,所以f(2e-x)的单调递增区间为(-∞,e),单调递减区间为(e,2e)。

又g(a)=0,符合要求。

又g(a)=0,与g(x)有且只有一个零点矛盾,故实数a的取值范围(0,e]。

②因为h(x)=①知,h(a-x)=-g(a-x)=g(a+x),h(a+x)=g(a+x)=h(a-x),故h(x)关于x=a轴对称,h(x)=2lna-2有4个根,如图1所示,其中x1与x4关于x=a对称,x2与x3关 于x=a对称。由①中分析可知,当a≤e时,g(x)单调递减,则h(x)=2lna-2 最多只有两个根,所以a>e,ax2=x3-a,x3-x2=2(x3-a)。不妨考虑x∈(a,2a),此时h(x)=g(x),记φ(x)=g(x)-(2lna-2)(x-a),由①得φ′(x)=g′(x)-(2lna-2)≤0,φ(x)是单调递减的,即φ(x)<φ(a)=0,即g(x)<(2lna-2)·(x-a)在x∈(a,2a)上恒成立。

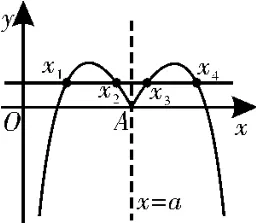
图1

由0=g(x3)+2-2lna<(2lna-2)·(x3-a)+2-2lna,可得x3>a+1,所以x3-a>1,即x3-x2>2。

当x∈(a,2a)时,(2a-x)lnx>(2ax)ln e>0,g(x)

点评:经历了由函数与方程之间的转化,通过“数”到“形”的构建,又由“形”到“数”的概括。在逻辑推理过程中,数学基础知识综合应用,数学思想方法相互渗透,数形结合与化归转化思想则起到了画龙点睛的作用。

函数与导数的综合问题,一直是历年高考试卷中最重要、占比最多的基本知识点之一,考查涉及小题(选择题或填空题)和大题(解答题),正因为其蕴含着丰富的数学思想方法,还涉及化归与转化、一般与特殊、类比等许多数学思维方法,因此,我们要在学习过程中,探索并充分体会其数学思想方法,巧妙思想引领,必会收到事半功倍的效果,全面提升数学能力。