垂尾装配尺寸链公差分析与优化

张 勇，余志明，陈里根，李根生

（航空工业洪都，江西 南昌，330024）

0 引言

在机械零件生产制造过程中，为保证零件的装配和互换，设计师在进行零件设计时往往允许零件存在一定的尺寸公差，避免影响到机械产品的质量和装配精度。在机械装配或零件加工过程中，离不开尺寸的计算问题，一组首尾相接的相互关联的尺寸形成一个尺寸链。尺寸链的合理使用对于保证产品质量、提高经济效益、降低生产成本具有重要意义[1]。一方面，在零件的加工过程中，根据加工工序，通过尺寸链的计算，保证每个工序的加工精度，从而确保零件的精度要求；另一方面，通过尺寸链的计算，可以得到间隙即封闭环的大小，判断其是否满足产品质量要求，从而以最经济的方案设计零件加工精度，保证零件互换性，达到预期目的。

某型机垂尾由垂尾安定面和方向舵组成，其中垂尾安定面由前后梁、外蒙皮、肋、长桁等结构组成。垂尾通过垂尾安定面的前后梁单耳接头与机身框双耳接头对接装配，单耳接头与双耳接头之间通过螺栓固定，如图1 所示。为保证垂尾的装配与互换，应避免基于经验式的尺寸公差分配而造成装配过程中的零件干涉，本文基于尺寸链对垂尾装配过程中相互关联的零件尺寸进行公差分析与优化，减少装配过程中现场不必要的修挫打磨量与加垫调整，提高装配效率。

图1 垂尾装配示意图

1 尺寸链

尺寸链是研究机械产品中尺寸之间的相互关系，分析影响装配精度与技术要求的因素，确定各有关零部件尺寸和位置的合适公差，从而求得保证产品达到设计精度要求的经济合理的方法[2]。

1.1 尺寸链定义与特性

在机械装配或零件加工过程中，由相互关联的尺寸连接形成的封闭尺寸组，称为尺寸链。其中，尺寸是包括长度、角度和形位公差的广义尺寸。

尺寸链特性：

1） 封闭性：组成尺寸链的各个尺寸按一定顺序构成一个封闭系统；

2） 相关性：尺寸链中一个尺寸变动将影响其他尺寸的变动。

1.2 尺寸链的组成及基本关系式

构成尺寸链的各个尺寸称为环，尺寸链的环分为封闭环和组成环。

封闭环：指加工或装配过程中最后自然形成的尺寸；

组成环：指尺寸链中除封闭环以外的其他环，根据其对封闭环的影响不同，又分为增环和减环。

1） 增环：与封闭环同向变动的组成环，同向变动指该组成环尺寸增大（或减小）而其他组成环不变时，封闭环的尺寸也随之增大（或减小）。

2） 减环：与封闭环反向变动的组成环，反向变动指该组成环尺寸增大（或减小）而其他组成环不变时，封闭环的尺寸也随之减小（或增大）。

设尺寸链中总环数为n，其中有m 个增环，则减环有 n-m-1 个，用 Ai、ESi、EIi、Ti、Δi分别表示增环基本尺寸、上偏差、下偏差、公差、中间偏差；用 A0、ES0、EI0、T0、Δ0分别表示封闭环基本尺寸、上偏差、下偏差和公差、中间偏差，根据完全互换法（又称极值法），对线性尺寸链，封闭环与组成环之间的关系式为：

对非线性尺寸链，需考虑传递系数ξ，如果是增环，ξ 取正值，减环 ξ 取负值，有：

完全互换法是按尺寸链的极限尺寸来计算公差。但是，由生产实践可知，在成批生产和大量生产中，零件实际尺寸的分布是随机的，多数情况下，考虑成正态分布或偏态分布。 换句话说，如果加工中工艺调整重心接近公差带中心时，大多数零件的尺寸分布于公差带中心附近，靠近极限尺寸的零件数目较少。因此，可利用这一规律，将组成环公差放大，这样不但使零件易于加工，同时满足封闭环的技术要求，从而获得更大的经济效果。当然，此时封闭环超出技术要求的情况是存在的，但其概率很小，所以这种方法称为概率法（又称大数互换法）[3]，其基本关系式为：

式中σ0、σi分别为封闭环和各组成环的标准偏差。 令传递系数为 ξ，则：i

式中：e 为相对不对称系数，k 为相对分布系数，e和k 的取值主要决定于加工工艺过程。大批量生产稳定的工艺过程，其工件尺寸趋近正态分布，取e=0，k=1[3]。

按照统计概率法，某独立随机事件重复试验n次，其统计结果应符合正态分布律，σ 为其正态分布图的均方差，在±3σ 范围内正态分布图的覆盖率占99.73%，因此，常用统计结果落在正态分布图的±3σ（即6σ） 范围内的概率来判断样品是否满足规定要求，这就是6σ 原则[4]。 对组成环和封闭环尺寸偏差服从正态分布，有Ti=6σi，此时封闭环的公差与组成环的公差关系为：

尺寸链分析的极值法和概率法求解过程如图2所示。

图2 求解过程

2.3 尺寸链分析步骤

不管是极值法还是概率法，传统尺寸链分析的基本步骤包括建立尺寸链线图、确定封闭环、判断增减环、求解未知量[5]。但对总环数较多的复杂尺寸链而言，增、减环的判断耗时易错，为解决这一问题，文献[6]提出“矢量五步法”：

1） 分析工况，找出要计算的尺寸（或间隙或过盈）；

2） 将该尺寸的两端点设定为起点和终点，划定从起点到终点的方向，即为正方向（+）；反之，即为负方向（-）；

3） 沿起点依次按顺序找出每一个首尾相接的关联尺寸（即组成环），并用箭头表示其方向，最终回到终点，形成一个封闭的链环，此时所有尺寸的方向已唯一确定；

4） 根据所绘制链环，箭头方向与正方向一致的尺寸为正尺寸，反之为负尺寸；

5） 基于零部件实际公差呈正态分布的假设，根据式（12）计算公差值。

2 垂尾装配

垂尾通过垂尾安定面的前、后梁单耳接头与机身框双耳接头对接装配，其对接示意图见图3。 前、后梁接头孔内两侧均安装有相同的带凸肩的圆环状衬套，起到保护梁且避免磨损的作用，各接头之间通过螺栓固定。为保证装配精度，机身框开有装配定位孔，其中两处中心定位孔轴线位于飞机对称面内，避免装配偏心。

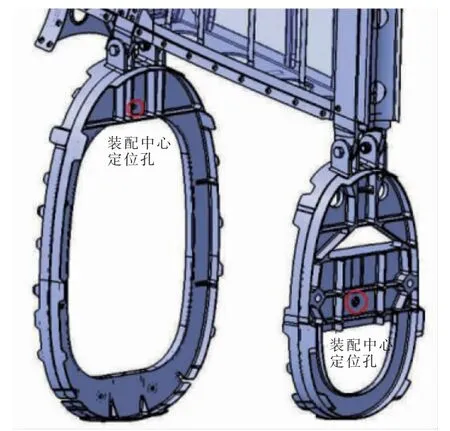
图3 对接示意图

设计时，为避免对接接头间隙过大，在装配附注中注有：垂直安定面左侧梁接头与机身框接头对接处耳片间隙大于0.3mm 时，需要加铝垫，垫片方向可按需调整。

3 垂尾装配尺寸链公差分析与优化

垂尾装配分两部分，先将垂尾各零件装配成整体，然后将垂尾对接到装配好的机身框接头上。装配对接涉及前后梁接头、框接头、衬套等零件尺寸，各零件尺寸如图4~图5 所示，单位为mm，根据装配现场前后梁左侧接头与机身框接头间间隙进行加垫，保证垂尾正常装配。

图4 前梁与框装配尺寸图

图5 后梁与框装配尺寸图

3.1 垂尾装配尺寸链分析

3.1.1 垂尾装配尺寸链绘制

根据垂尾装配尺寸关系，对垂尾装配进行尺寸链分析。 一方面，由于前、后梁与机身框对接形式一样，为避免垂尾整体装配受前、后梁对接顺序影响，前、后梁接头，前、后框接头相互对应尺寸的上下偏差相同；另一方面，由于垂尾是整体与机身框对接，前、后梁对接相互影响，需考虑一方装配好后另一方与框接头对接是否会产生干涉从而影响装配，故需考虑前、后梁装配尺寸链间的相互影响。

由图6 所示，设计时考虑左侧梁接头加垫，故分析时假设后梁右侧单耳接头、衬套凸肩，机身框右侧的双耳外侧接头相互贴合，前后梁对接尺寸示意如图7~图8 所示，根据矢量五步法绘制垂尾装配尺寸链。

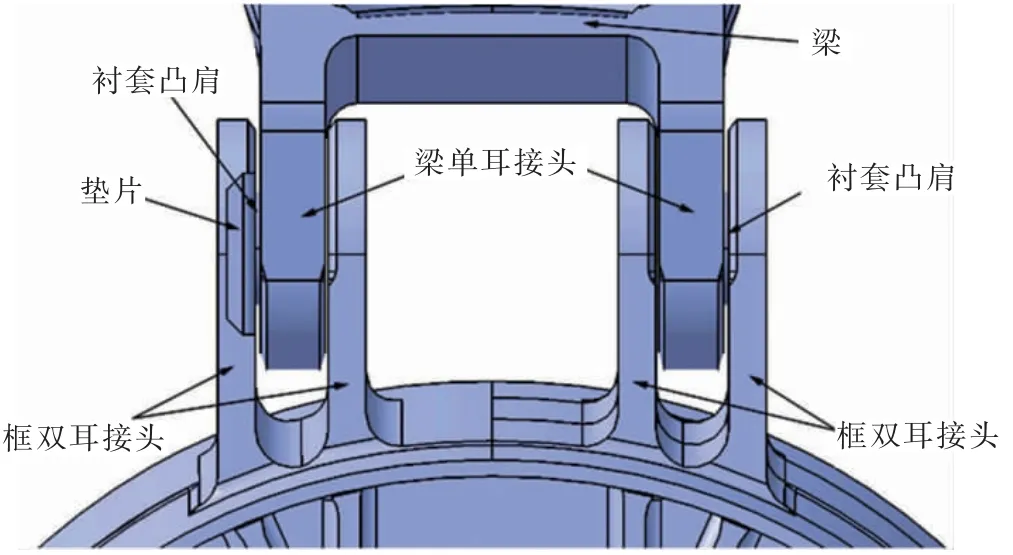
图6 梁与框对接示意图

图7 后梁尺寸示意图

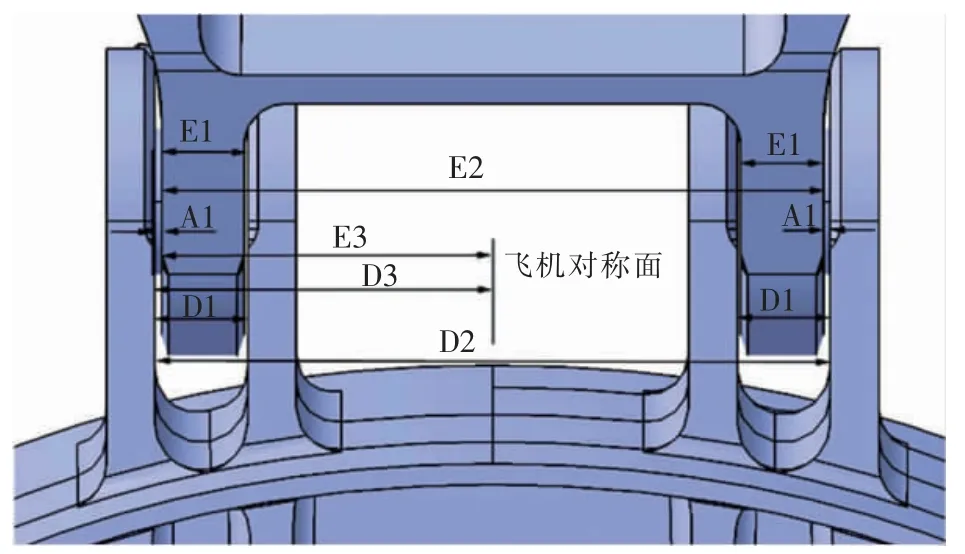
图8 前梁尺寸示意图

＞后梁装配尺寸链

1） 后梁两侧接头与机身框两侧的双耳接头对接装配尺寸链：

图9 尺寸链中，X1 为闭环，用于检验后梁左侧接头对接时左端是否干涉，或间隙加垫调整，A1、B2 为减环，C2 为增环。

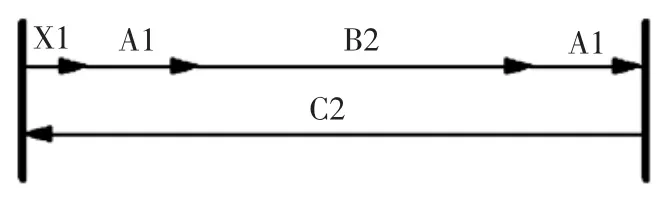
图9 后梁与机身框对接尺寸链-1

2） 梁两侧单耳接头分别与机身框双耳接头对接装配尺寸链：

左侧接头对接尺寸链如图10 所示。

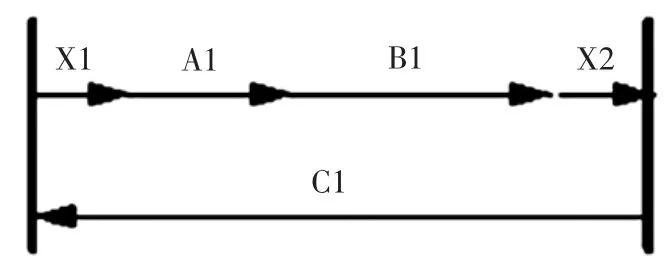
图10 后梁左侧接头对接尺寸链-2

图10 尺寸链中，X2 为闭环，用于确定后梁左侧接头对接时右端是否干涉，此时X1 为过渡环，B1、C2为减环，A1、C1、B2 为增环。

右侧接头对接尺寸链如图11 所示。

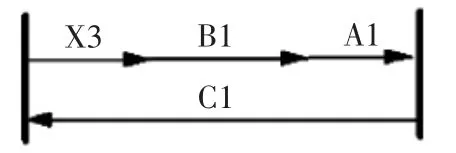
图11 后梁右侧接头对接尺寸链-3

图11 尺寸链中，X3 为闭环，用于确定后梁右侧接头对接时左端是否干涉，A1、B1 为减环，C1 为增环。

故有：X3＝C1-A1-B1

＞前后梁相互影响尺寸链

后梁装配对接时会影响前梁对接，由于前、后框都通过中心定位孔安装，垂尾整体安装在机身框上，故前后梁对接尺寸链可通过中心定位孔轴线（飞机对称面）传递，尺寸链如图12 所示。

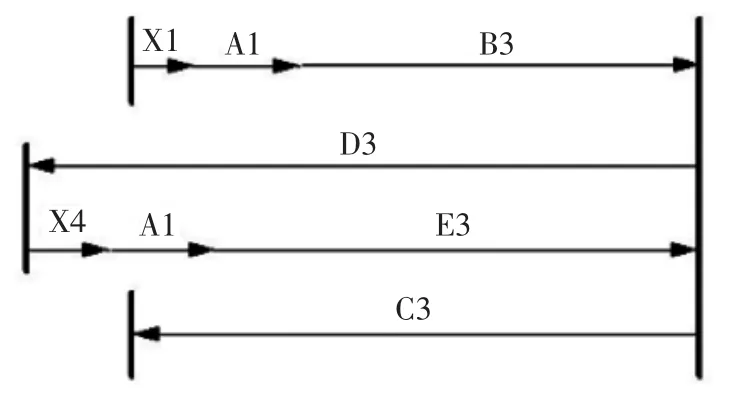
图12 前后梁传递尺寸链-4

图12 尺寸链中，X4 为闭环，用于检验前梁左侧接头对接时左端是否干涉，或间隙加垫调整，X1 为过渡环，A1、B3、E3 为减环，D3、C3 为增环。

＞前梁装配尺寸链

前梁装配尺寸链同后梁装配尺寸链，如图13 所示。

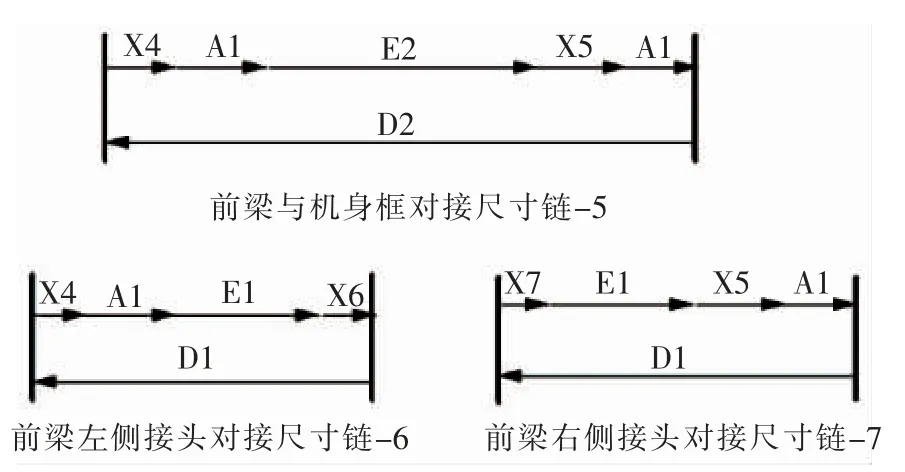
图13 前梁装配尺寸链

图13 尺寸链-5 中，X5 为闭环，用于检验前梁右侧接头对接时衬套与框接头是否干涉，X4 为过渡环，A1、E2 为减环，D2 为增环。

尺寸链-6 中，X6 为闭环，用于确定前梁左侧接头对接时右端是否干涉，X4 为过渡环，A1、E1 为减环，D1 为增环。

尺寸链-7 中，X7 为闭环，用于确定前梁右侧接头对接时左端是否干涉，X5 为过渡环，E1 为减环，D1为增环。

3.1.2 垂尾装配尺寸链求解

根据上述尺寸链-1 至-7，采用极值法和概率法对尺寸链未知量（闭环）进行求解。

对尺寸链-1，极限法求解为：

对于稳定的生产工艺过程，取垂尾零件加工后的尺寸服从正态分布，故概率法求解为：

极限法和概率法进行尺寸链分析结果如表1 和表2 所示。

表1 极值法求解结果

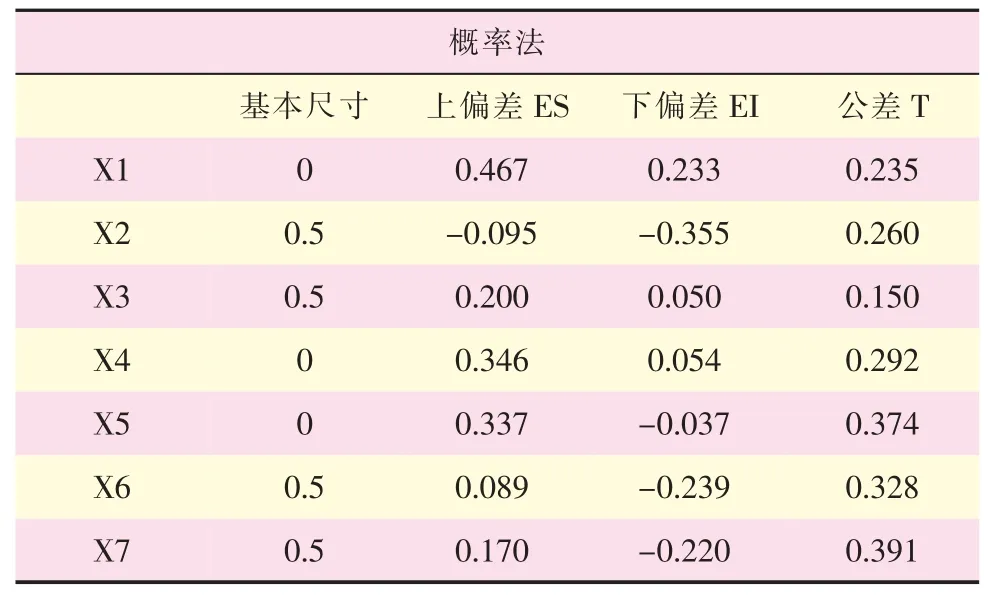
表2 概率法求解结果

由表1 和表2，得到极值法和概率法闭环X1-X7尺寸范围，如表3 所示，其公差及最小极限尺寸对比如图14 和图15 所示。

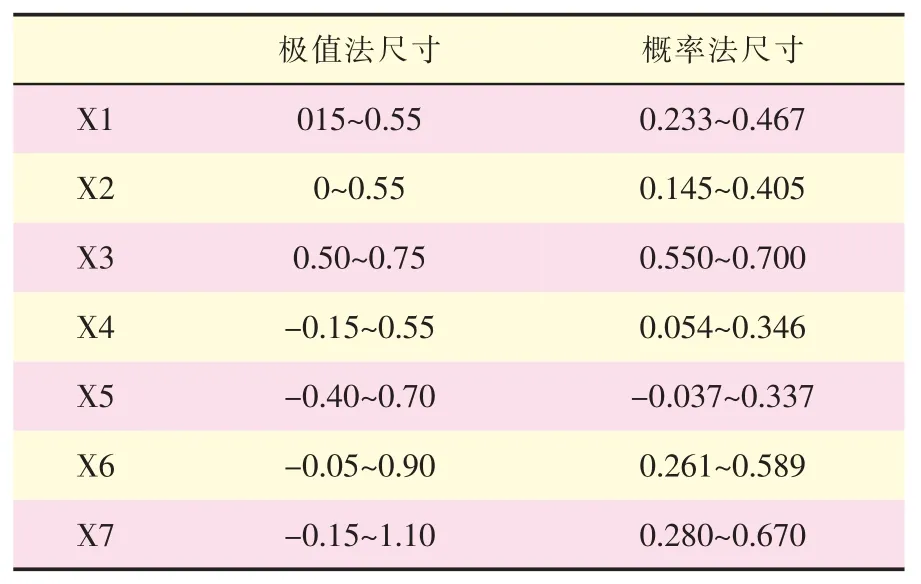
表3 极值法与概率法对比

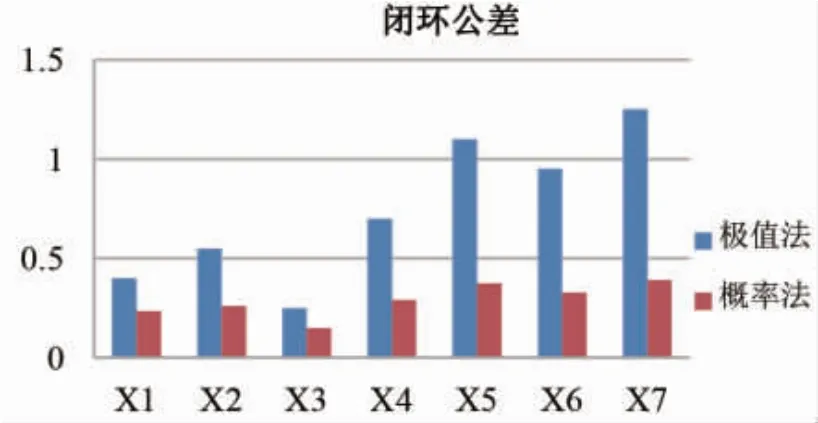
图14 公差对比

由表 3、图 14 和图 15 可知，

图15 最小极限尺寸对比

1） 极值法求解的闭环公差大于概率法求解的闭环公差，而闭环是最后形成的尺寸，非实际零件加工尺寸，其公差大。为保证零件完全互换，相应的零件需要较高的加工精度，增加了制造加工成本。

2） 闭环中，无论是极值法还是概率法，都存在最小极限尺寸小于0 的情况，说明后梁装配好后，前梁与框对接时接头存在干涉的可能， 需对接头进行修挫打磨，增加了装配工作量；其中极值法X4、X5、X6、X7 的最小极限尺寸都小于0， 说明前梁与框对接时左、右接头都存在干涉的可能，需要对左、右接头进行修挫打磨，保证完全互换，而概率法中只有X5 的最小极限尺寸小于0，说明前梁右侧对接接头存在干涉的可能，需对右侧接头进行修挫打磨。

3） 相较于极值法，概率法更符合生产实际，垂尾装配出现不合格性更小，无需多次修挫打磨，有较大的经济效果。

4） 极值法和概率法求解X1 和X4 的最大极限尺寸均大于0.3，故装配时，根据装配要求，需在前梁和后梁左侧加铝垫。

3.2 垂尾装配尺寸链优化

根据尺寸链分析可知，垂尾装配对接时，无论是极值法还是概率法，都存在接头间相互干涉的可能，为减少装配过程中现场的修挫打磨，对装配中尺寸链的公差进行优化，调整各尺寸的上下偏差，使封闭环最小极限尺寸不小于0，保证垂尾装配对接时接头间存在一定间隙，即：

优化后零件的各尺寸如表4 所示。

表4 优化后尺寸

由表 5 可知，零件尺寸 A1、B1、C1、D1、E1 的公差增大，至少翻倍，即衬套凸缘厚度，前、后梁接头厚度，机身框双耳接头宽度公差放宽，无需高精度，极大提高了零件加工经济性；其余尺寸公差减小，需提高零件加工精度，保证接头对接时留有一定间隙，减少后续现场装配修挫打磨，增加了工作量。

优化后用极值法和概率法求解封闭环尺寸，结果如表5 和表6 所示。

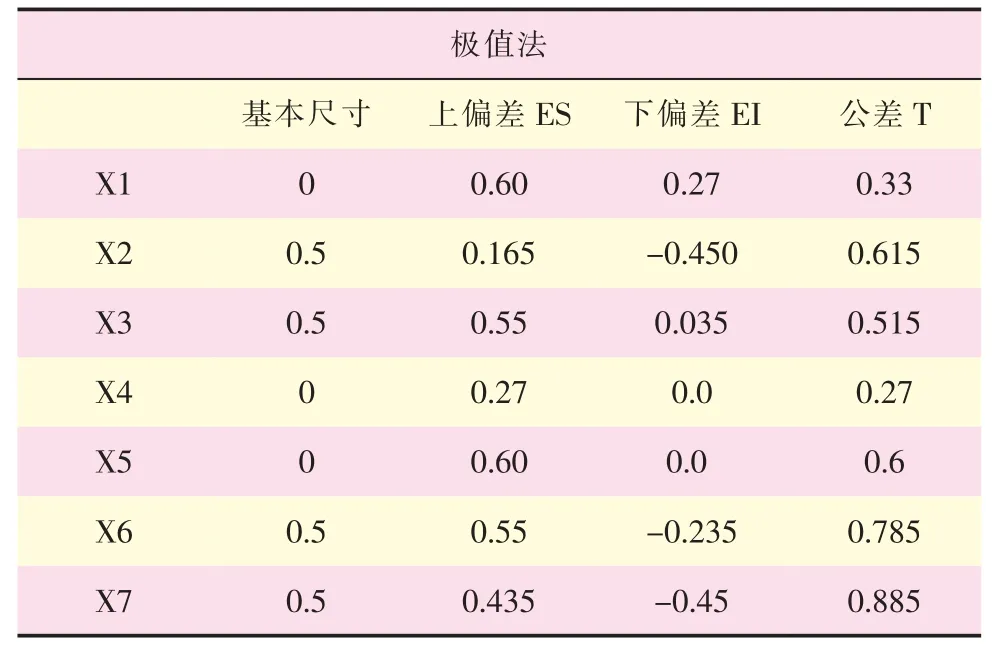
表5 优化后极值法求解结果

表6 优化后概率法求解结果

优化前后闭环最小极限尺寸对比如表7 所示，其柱状图如图16、图17 所示，由此可知：

图16 极值法最小极限尺寸对比

图17 概率法最小极限尺寸对比

表7 优化前后闭环最小极限尺寸对比

1） 经过零件尺寸优化， 极值法和概率法求解的闭环最小极限尺寸均增大且均不小于0，即垂尾现场装配对接时，不存在接头间干涉现象，无需进行零件的修挫打磨，可实现垂尾装配的完全互换。

2） 两种方法求解X1 的最大极限尺寸均大于0.3，而X4 的最大极限尺寸均小于0.3，故装配时，只需在后梁左侧加铝垫，前梁无需加垫。

4 结语

本文基于尺寸链，考虑垂尾整体装配时，其前、后梁与机身框对接的相互影响，利用尺寸链的空间传递，绘制了垂尾装配对接相关尺寸链，并采用极限法和概率法进行尺寸链的公差分析。分析表明，垂尾装配对接时接头间存在干涉，且均需在梁的左侧加铝垫。 为减少现场装配时的修挫打磨量，对尺寸链公差进行优化，调整各零件尺寸的上下偏差，即零件的加工精度，优化后极值法和概率法求解零件间间隙值均不小于0mm，保证了垂尾正常装配，装配效率得到提高，且只需在前梁和后梁一方的左侧加铝垫，无需双方均进行加垫调整，减少了不必要的重量。