T800碳纤维/PEEK热塑性复合材料的拉伸与剪切失效行为研究①

王晋忠,宋学宇,李飞皓,刘 凯,王 莹,葛敬冉

(1.海军装备部,西安 710018;2.中国航天科技集团有限公司四院四十一所,西安 710025;3.西北工业大学 航天学院,西安 710072;4.北京理工大学 先进结构技术研究院,北京 100081)

0 引言

相比于传统热固性复合材料,热塑性树脂基复合材料具有优异的抗冲击韧性、耐疲劳、高热稳、抗蠕变、生产效率高、可长期贮存、可回收再利用等一系列优点。因此,逐渐在航空航天、生物医疗、交通运输、石油化工等领域得到了广泛研究和应用[1-2]。尤其是采用聚醚醚酮(PEEK)、聚芳醚酮等先进芳香族热塑性树脂基体的高性能碳纤维增强热塑性复合材料,具有突出的耐高温、承载效率高等综合性能,在固体火箭发动机复合材料壳体方向具有巨大的应用潜力,非常符合其进一步轻量化、耐高温、成型效率高的应用需求。因此,在工艺成型、承载性能等方面得到了众多研究单位和学者的关注和研究[3-4]。目前关于高性能碳纤维热塑性复合材料的研究主要集中在工艺成型方面[5-6]。

纤维复合材料在复杂力学载荷环境作用下具有纤维断裂、树脂基体开裂、复合材料分层等多种损伤失效行为,并且各种损伤失效行为相互耦合,导致纤维复合材料的损伤失效行为异常复杂,从而难以对其进行精准分析和描述。针对复合材料渐进损伤失效行为的研究,HUANG[7]研究了一种基于复合材料细观力学侨联模型的基本理论和使用方法,相比于常用的细观力学模型,侨联模型能够对复合材料细观纤维、树脂的应力进行精准分析;结合复合材料的失效准则,能够更加准确的预测单向复合材料的强度和刚度。王晓强等[8]基于细观力学理论模型,建立了单向纤维增强复合材料的代表性体积单元(RVE)模型,用有限元方法分析了典型复合材料内在组分材料对结构宏观力学性能的影响。RAMIREZ等[9]基于2D、3D的连续介质损伤力学模型对拉伸载荷下含有缺口的缠绕复合材料板型试件的损伤失效行为进行了研究,仿真分析结果与试验残骸的宏观形貌、X射线、光学照相等分析结果吻合较好,证明了该渐进损伤失效模型用于分析缠绕复合材料结构微观失效行为的准确性。REINER等[10]采用两种渐进损伤失效模型对IM7/8552碳纤维复合材料层合板在拉伸载荷下的破坏行为进行了研究,并通过试验测试方法对两种失效模型的有效性进行了评估研究,结果表明面内损伤失效模型可以有效模拟复合材料载荷试验下的破坏行为。对于复合材料粘接界面损伤失效机理,CAROLLO等[11]提出了一种新的三维有限元方法,可以模拟非均质材料中脆性裂纹扩展与界面分层之间的相互作用。在大变形分析的框架内,将脆性断裂的相场模型与内聚力模型耦合。对弯曲平板几何形状结构在平面内和平面外加载条件下的断裂失效行为进行了模拟,评估了所提出的预测模型的分析能力。LIN等[12]提出了一种将连续介质损伤力学模型和内聚力模型耦合的有限元分析技术——连续介质脱粘有限元技术(CDFE),在材料损伤破坏之前,采用连续介质损伤力学进行模拟,当微观裂纹产生后,在该区域引入内聚力模型,并通过断裂力学的方法对损伤演化行为进行模拟研究。顾志平[13]基于内聚力理论,运用有限元分析软件ABAQUS与用户单元子程序UEL发展了零厚度的三角形内聚力模型和一种改进的Xu-Needleman幂指数内聚力模型,通过碳纤维复合材料在压缩和弯曲载荷作用下的分层失效模拟,研究了内聚力形状、内聚力强度、网格尺寸对数值收敛性和网格敏感性的影响规律。

综上所述,已有关于纤维复合材料各种微细观模型的分析验证主要通过热固性碳纤维复合材料的破坏试验进行,本文则基于T800/PEEK高性能碳纤维热塑性复合材料预浸料,采用高温模压方法,制备单向复合材料,对其不同方向的拉伸、面内剪切刚度和强度进行试验测试。针对T800/PEEK单向复合材料结构特点,建立了RVE模型和复合材料内在纤维、基体、界面三种组分材料的本构关系,并基于渐进损伤失效模型和内聚力模型,考虑Benzeggagh-Kenane(BK)界面损伤演化准则,开展有限元模型在单轴拉伸/压缩和面内剪切载荷作用下的失效行为分析,将有限元模型计算结果与热塑性纤维复合材料试验结果进行对比。

1 试样制备及试验方法

1.1 试样制备

本文研究的T800/PEEK复合材料由T800碳纤维和自主研发的高增韧PEEK基体制备,是一种单向纤维铺层结构。该复合材料采用预浸料铺制,机压400 ℃、3 MPa固化成型工艺制备。表1与表2分别为T800碳纤维及PEEK树脂的性能参数。

表1 T800碳纤维性能参数

表2 PEEK树脂性能参数

依据GB/T 3354—1999《定向纤维增强聚合物基复合材料拉伸性能试验方法》,进行纵向(纤维方向与拉伸方向成0°夹角)单轴拉伸试验及横向(纤维方向与拉伸方向成90°夹角)拉伸试验,试样每组均不少于3个。图1(a)为T800/PEEK单向复合材料纵向拉伸试件的照片及外形尺寸,应变片为纵向粘贴,试件横截面尺寸见表3;图1(b)为T800/PEEK单向复合材料横向拉伸试件照片及外形尺寸,应变片采用纵向粘贴,试件横截面尺寸见表3。

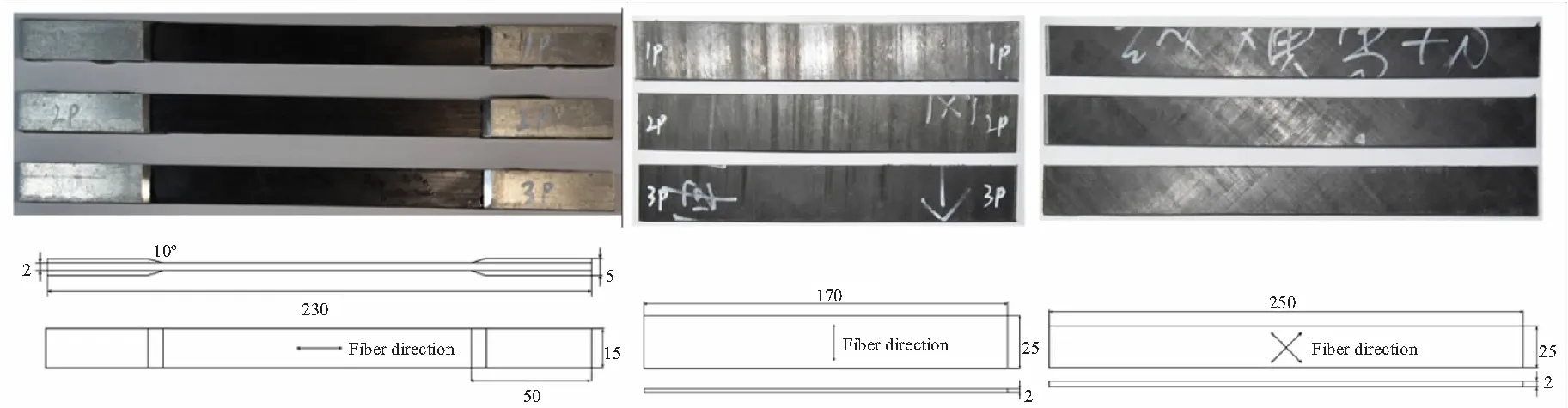
(a)Longitudinal tensile specimen (b)Transverse tensile specimen (c)In-plane shear specimen

依据GB/T 3355—2005《纤维增强塑料纵横剪切试验方法》进行面内剪切试验,试样每组不少于3个。图1(c)为T800/PEEK面内剪切试件照片及外形尺寸,应变片采用纵向黏贴,试件横截面尺寸见表3。

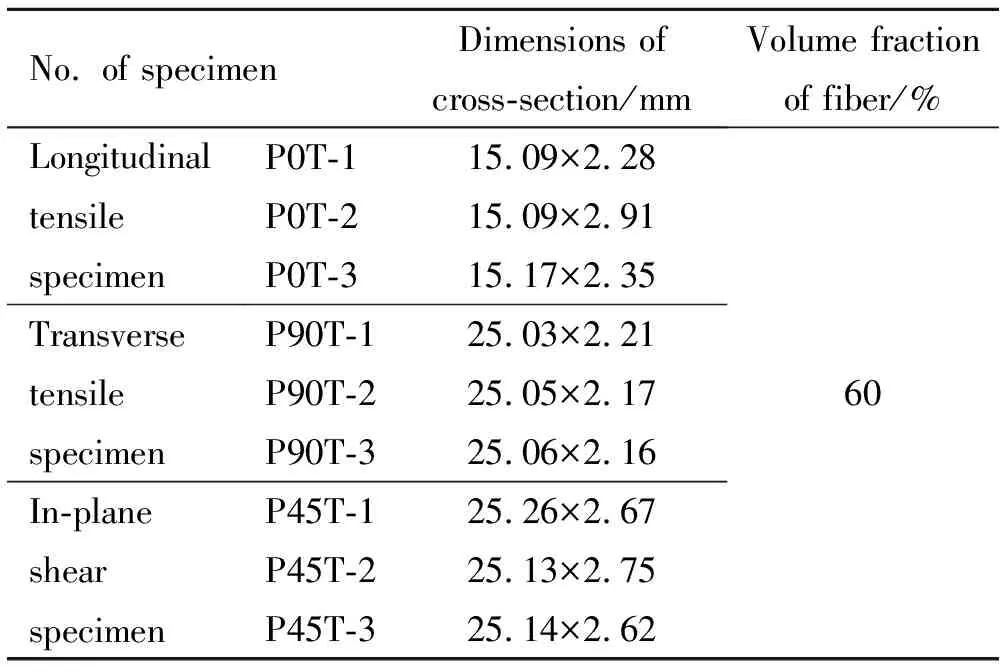
表3 试样尺寸

1.2 试验方法

参照拉伸试验标准,T800/PEEK单向复合材料纵向拉伸、横向拉伸和面内剪切试验使用INSTRON 100 kN液压伺服试验机在1mm/min的恒定加载速度和室温下进行。试验中均采用高精度应变片以准确测量试验过程中的应变,确保采集的数据能够代表材料的真实特性。

拉伸试验设备如图2所示,每组试验重复测试不少于3个试件。

图2 拉伸实验加载机

2 试验结果与分析

2.1 纵向(0°)单轴拉伸试验

T800/PEEK单向复合材料纵向(0°)单轴拉伸试样破坏形貌如图3所示,所有复合材料试件均在工作段发生纤维断裂,纤维的断口位置有一定波动性。纵向单轴拉伸试验应力-应变曲线如图4所示。

图3 T800/PEEK纵向拉伸破坏模式

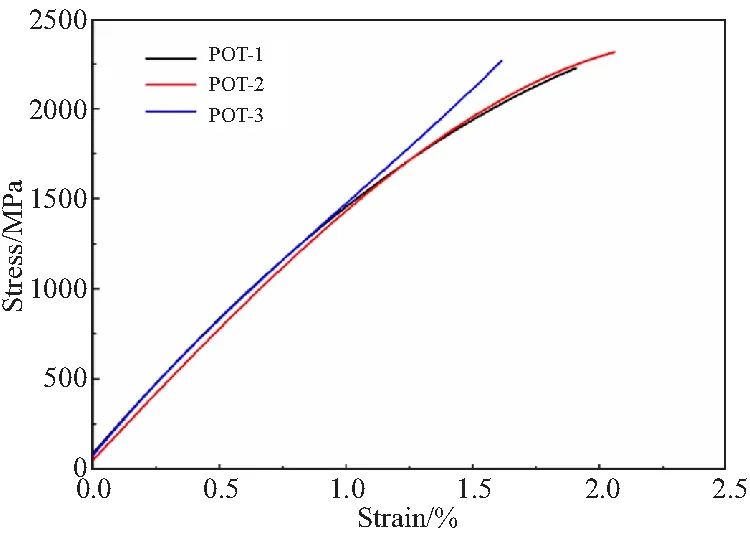
图4 T800/PEEK单向复合材料纵向拉伸应力-应变曲线

根据应力-应变试验曲线计算材料的纵向弹性模量,根据试件横截面积以及断裂应力计算纵向拉伸强度,纵向拉伸试验测试结果如表4所示。

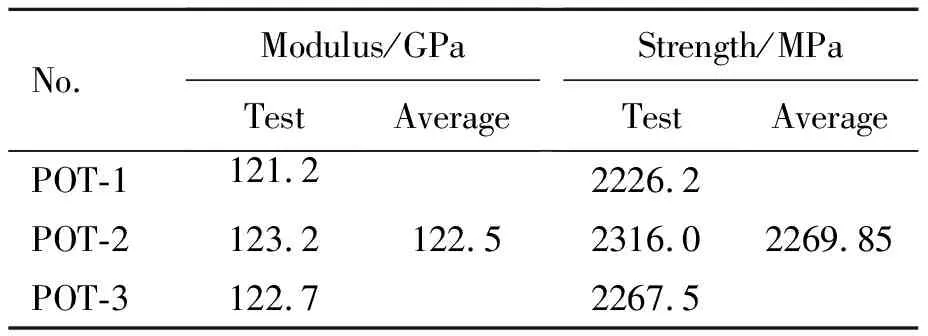
表4 T800/PEEK单向复合材料纵向拉伸实验结果

2.2 横向(90°)单轴拉伸试验

T800/PEEK单向复合材料横向(90°)单轴拉伸试样破坏形貌如图5所示,所有试件均在工作段断裂,断口较为整齐。横向单轴拉伸应力-应变曲线如图6所示。根据应力-应变试验曲线计算横向拉伸弹性模量,并根据试件横截面积以及断裂应力计算横向拉伸强度,试验结果如表5所示。

图5 T800/PEEK横向拉伸破坏模式

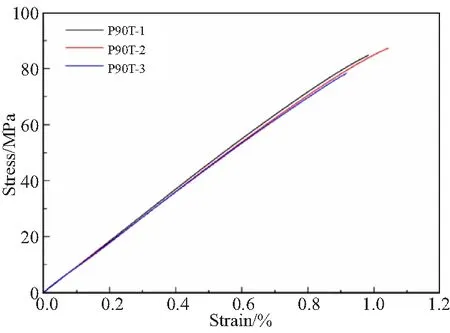
图6 T800/PEEK单向复合材料横向拉伸应力-应变曲线

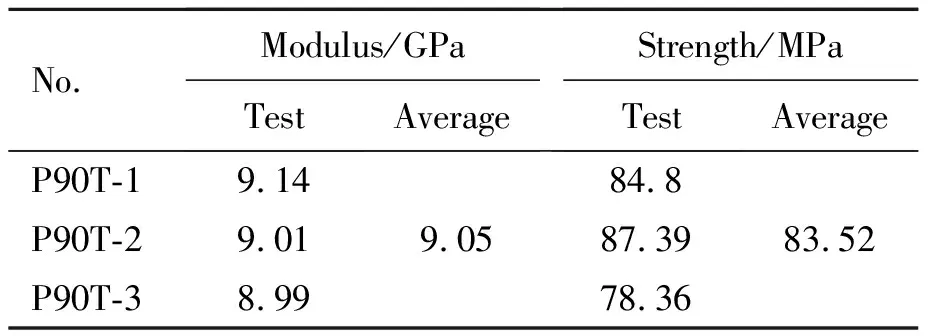
表5 T800/PEEK单向复合材料横向(90°)拉伸实验结果

2.3 面内剪切试验

T800/PEEK复合材料试样在面内剪切试验过程中产生较大的变形,破坏形貌如图7所示,样件断口呈45°断裂,且分层较明显。面内剪切应力-应变试验曲线如图8所示。根据应力-应变试验曲线计算剪切模量,选取发生5%应变处的应力作为失效强度,得到面内剪切试验测试结果如表6所示。

图7 T800/PEEK面内剪切破坏试样图

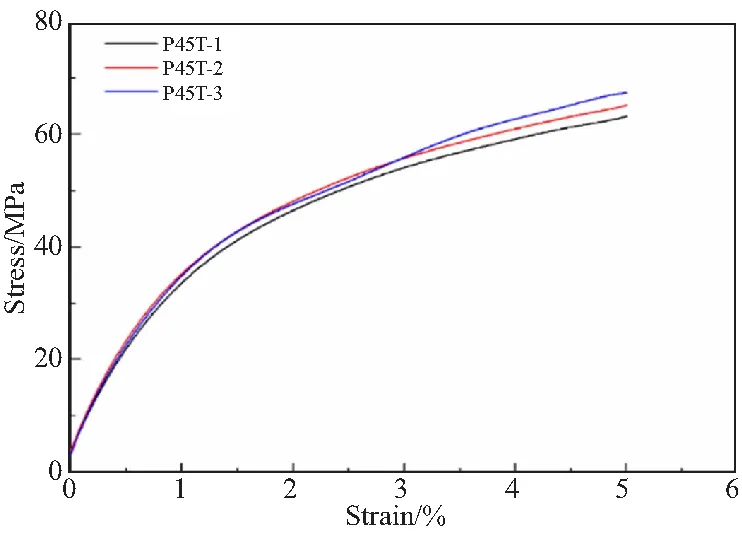
图8 T800/PEEK单向复合材料面内剪切应力-应变曲线

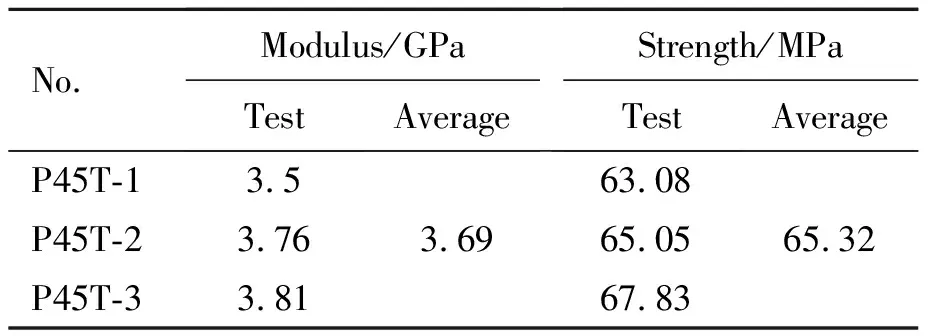
表6 T800/PEEK单向复合材料面内剪切试验结果

3 有限元仿真分析

3.1 单向复合材料代表性体积单元的建立方法

单向复合材料是由数千根碳纤维与树脂基体经过复合工艺固化而得到的单向增强材料,碳纤维的空间分布呈现出随机分布的特征,见图9(a)。因此,在单向复合材料代表性体积单元的选取方面,必须能够反映出纤维的随机分布特点,又不至于有限元模型网格太多导致无法计算。不同尺寸的RVE模型预测的模量或强度对比见图9(b),可以发现,当单胞模型较小时,其预测值波动较大;当单胞模型较大时,其纤维分布的随机性比较好,故其预测值逐渐收敛。

(a)Random distribution of fibers observed by SEM

经过试算不同尺寸的RVE发现,当单向复合材料的RVE边长大于10倍纤维直径的时候,其预测值波动范围会低于5%,故本项目的单向复合材料RVE模型皆按此标准建立[14]。首先,在给定RVE区域随机生成第一根纤维的坐标;然后,依次随机生成第二根、第三根等纤维且保证与已存在纤维不重合,直至满足额定纤维体积分数。

单向复合材料的代表性体积单元模型见图10。T800碳纤维直径为5.1 μm,单胞的尺寸为55.4 μm×55.4 μm×8 μm,其宽度满足大于10倍碳纤维直径的要求[14],并采用周期性边界条件[15]。

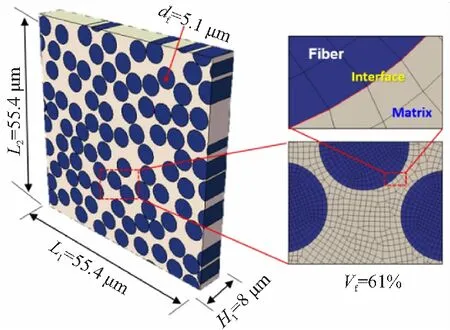
图10 单向复合材料的代表性体积单元模型

3.2 组分材料的本构关系

对T800/PEEK复合材料微细观结构进行局部放大观察,发现其包含三种组分材料,即碳纤维、PEKK树脂基体以及它们之间的界面,该小节主要研究讨论这三种组分材料的本构关系。

(1)碳纤维本构模型

碳纤维表现出横观各向同性的性能,其本构关系为

σf=Cf:εf

(1)

式中Cf为碳纤维的刚度矩阵。

在碳纤维的应力达到强度后,碳纤维表现出脆性断裂[16],最大拉压应力失效准则被用来判断碳纤维的损伤起始,定义如下:

(2)

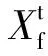
碳纤维的材料参数见表7。

表7 T800碳纤维的材料参数

(2)PEEK树脂本构模型

对于树脂基体,其为各向同性材料,PEEK树脂基体力学性能参数见表8。采用弹塑性损伤[17-18],损伤本构方程为

表8 PEEK树脂基体力学性能参数

(3)

(4)

(5)

假设不发生损伤的应力状态,基体的有效应力可表达为

(6)

基体采用Mises失效准则[19]:

式中σm,t和σm,c分别为基体的拉伸强度和压缩强度。

当基体达到其强度值后,损伤演化准则[20]为

Fm,J=φm,J-rm,J(J=t,c)

(9)

式中φm,J为基体的载荷方程;rm,J为基体的损伤阀值因子,损伤阀值因子是以1为初值,并随着材料的损伤演化和载荷的累积,逐渐增加。

由于材料的破坏是一个热力学不可逆过程,所以损伤阀值因子rm须满足Kuhn-Tucker和相容性条件:

(10)

(11)

对方程进行积分,就可以得到损伤阀值因子rm的表达式。基体的损伤阀值因子rm可以表达为

(12)

式中t为加载时间。

基体的破坏模式和碳纤维脆性断裂有所不同,树脂基体在准静态拉伸和压缩载荷都具有一定的塑性[21]。因此,本项目采用指数形式的弹塑性损伤模型来表征基体的损伤[22],如图11所示。

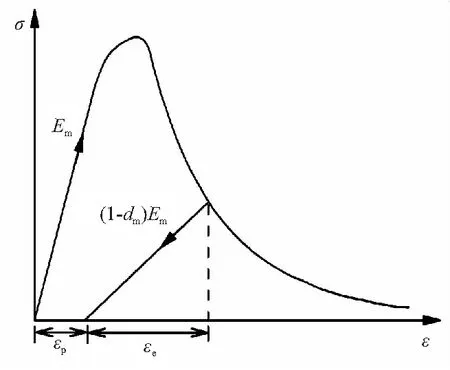
图11 基体的弹塑性损伤演化模型[22]

基体的损伤因子可表示为

损伤演化参数的确定。在损伤模型的有限元计算中,当组分材料达到初始破坏准则后,组分材料的刚度由于出现损伤而减小,表现局部软化特征。当减小有限元网格时,能量释放也随之减小。因此,数值模拟结果非常依赖于有限元网格大小。为了避免有限元网格尺寸对计算结果的影响,所有的退化参数A都是对其应力-应变关系曲线中应力退化段进行正则化得到。基于Bazant裂纹带理论[23],单位体积释放的能量gm可由其材料的能量释放率Gm,c确定:

(14)

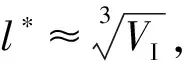
单位体积释放的能量gm可通过能量耗散率积分得

(15)

式中G为Helmholtz自由能。

由方程可得

(16)

通过上式得到的损伤参数可以确保通过数值模型计算的能量耗散独立于网格密度。通常应变软化会导致隐式分析求解的收敛困难,一般采用引入粘性系数的Duvaut-Lions模型[24]来改进数值计算的收敛性。定义粘性损伤变量为

(17)

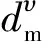
上式在有限元中可以利用差分方法求解,第n+1步的规则化损伤变量为

(18)

(19)

(20)

式中Ct为材料的切线刚度矩阵,也称雅可比矩阵。

在子程序UMAT中,为使非线性问题较快收敛,需计算材料的雅可比矩阵。基体的切线刚度矩阵为

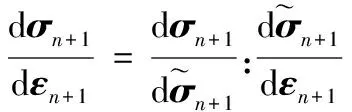
(21)

(3)界面本构模型

界面破坏是复合材料最常见的失效形式,本文界面用零厚度的内聚力单元进行描述,界面的损伤本构关系为

ti=(1-d)Kiδi(i=n,s,t)

(22)

式中ti为界面的张力分量;Ki为界面刚度;δi为界面位移。

这里,四阶最大正应力失效准则被用来判断界面失效的起始,定义如下:

(23)

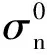
基于能量的Benzeggagh-Kenane(BK)损伤演化准则被用来描述界面的损伤扩展[26],定义如下:

(24)

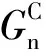
表9给出了界面的材料参数[27],图12为内聚力界面本构的示意图。

表9 界面的材料参数[27]

3.3 不同载荷作用下的单向复合材料失效模式分析

(1)纵向单轴拉伸/压缩载荷作用下单胞模型的失效行为对建立的单向复合材料代表性体积单胞施加轴向拉伸与压缩载荷,预测的应力-应变曲线见图13,纵向拉伸模量的预测值约为130 GPa,而实验值约为122.5 GPa,误差在10%以内;单轴拉伸强度的预测值约为2510 MPa,而实验值约为2269.85 MPa,误差在11%以内;单轴压缩强度的预测值约为1220 MPa。纵向单轴拉伸的失效模式见图14,可以看出,RVE受单轴拉伸时,由于纤维的模量与强度比基体高很多,主要失效模式为纤维的脆性断裂,并且靠近界面的基体产生明显的塑性变形与失效,最终单向复合材料由于纤维拔出断裂而失效。纵向单轴压缩的失效模式见图15,纤维受压缩导致脆性断裂,伴随着纤维周围基体的塑性变形及失效,但基体失效不如单轴拉伸时严重。

(2)横向单轴拉伸/压缩载荷作用下单胞模型的失效行为

对建立的单向复合材料代表性体积单胞施加横向拉伸与压缩载荷,预测的应力-应变曲线见图16,横向拉伸模量的预测值为9.15 GPa,而实验值为9.05 GPa,误差在10%以内;横向拉伸强度的预测值约为75.3 MPa,而实验值为83.52 MPa,误差在10%以内;横向压缩强度的预测值约为115.3 MPa。横向载荷作用下,单向复合材料的失效主要由基体及界面决定,纤维并不会发生破坏。横向拉伸载荷作用下的失效模式见图17,可以清晰看出界面脱粘及靠近界面处的基体失效,为横向拉伸载荷下的主要失效模型。横向压缩载荷作用下的失效模式见图18,可以看出,基体的剪切破坏为其主要失效模式,单胞呈现出约为56°的剪切破坏,与实验观测吻合。

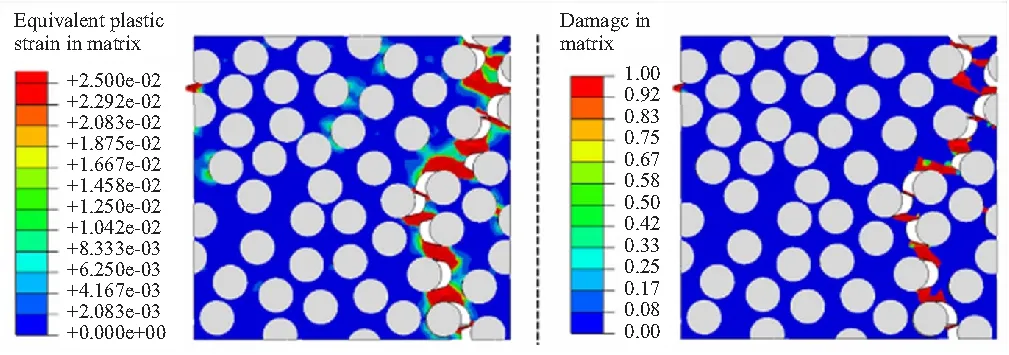
(a)Distribution of equivalent plastic strain in matrix (b)Damage distribution in matrix

(a)Distribution of equivalent plastic strain in matrix (b)Damage distribution in matrix

(3)面内剪切载荷作用下单胞模型的失效行为

对建立的单向复合材料代表性体积单胞施加纯剪切载荷,预测的应力-应变曲线见图19,剪切模量的预测值约为3.75 GPa,实验值约为3.69 GPa,误差在5%以内;剪切强度的预测值约为62.3 MPa,实验值为 65.32 MPa,误差在5%以内。纯剪切作用下,单向复合材料失效主要由基体及界面决定,纤维不会发生破坏。纯剪切载荷作用下的失效模式见图20,界面脱粘及基体剪切破坏为主要失效模式。

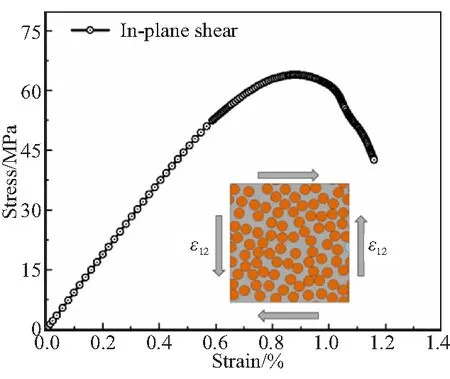
图19 面内剪切应力-应变曲线

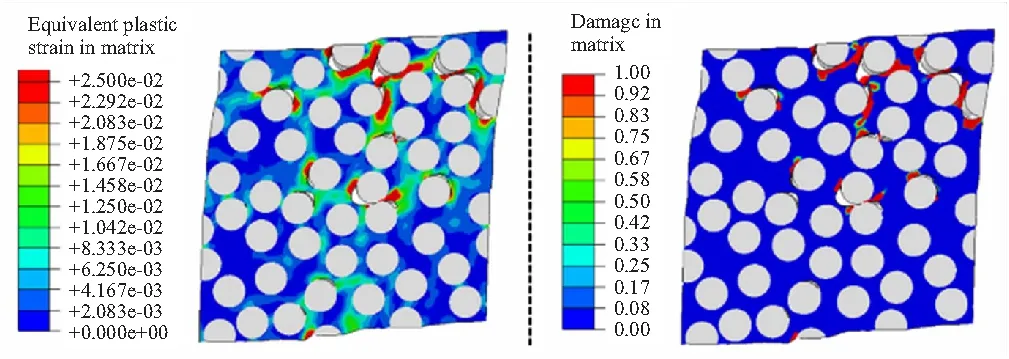
(a)Distribution of equivalent plasticstrain in matrix (b)Damage distribution in matrix

4 结论

(1)采用模压方式制备了T800/PEEK高性能碳纤维热塑性复合材料,对其进行了纵/横向单轴拉伸和面内剪切实验,得到了材料在不同载荷方式作用下的模量、强度和破坏模式,不同载荷作用下的材料破坏模式符合预期形式。T800/PEEK复合材料的纵向拉伸模量达到122 GPa,强度达到2269 MPa;横向拉伸模量达到9 GPa,强度达到83 MPa。

(2)针对T800/PEEK复合材料的微细观结构特点,建立了单向复合材料的RVE模型,采用弹塑性损伤模型和Benzeggagh-Kenane损伤演化准则建立了树脂基体的损伤本构关系和界面内聚力模型,对T800/PEEK单向复合材料在单轴拉伸/压缩和面内剪切载荷作用下单胞模型的失效行为进行了预测。有限元模型预测与实验测试结果吻合良好,其中拉伸模量/强度相差最大为11%,剪切模量/强度相差最大为5%,证明本文有限元模型预测的有效性。

本文建立的纤维/树脂复合材料有限元模型,同时揭示了T800/PEEK复合材料在典型力学工况作用下的损伤失效机理,为后续相关研究提供技术基础。