HEDM推进剂的非线性粘弹损伤本构及其细观损伤演化研究①
2023-04-26刘琪琪王春光张恺宁郭振宇
刘琪琪,王春光,2*,张恺宁,李 群 ,郭振宇
(1.西安交通大学 航天航空学院,机械结构强度与振动国家重点实验室,西安 710049;2.北京凌空天行科技有限责任公司,北京 100176;3.西安航天化学动力有限公司,西安 710025)
0 引言
为了满足未来生产高性能导弹武器的需要,必须开发更为高能的新型固体推进剂。目前广泛使用的推进剂主要有丁羟推进剂(Hydroxyl Terminated Polybutadiene, HTPB)[1]、硝酸酯增塑的聚醚聚氨酯(Nitrate Ester Plasticized Polyether, NEPE)推进剂[2]以及各类复合推进剂[3-4]等。聚叠氮缩水甘油醚(Glycidyl Azide Polymer, GAP)因其高燃烧速率、低火焰温度、良好的热稳定性等特点被作为优良的粘合剂广泛用于生产各类高能推进剂[5-7]。基于对高能推进剂的发展需求,以GAP基夹杂各类氧化剂的高能推进剂被提出并受到广泛关注。
目前,对于GAP基推进剂在热分析以及基础的力学性能两方面都有较为深入的研究。WANG等[8]对CL-20/GAP推进剂进行了热重分析及差热分析,并对其进行了扫描电镜实验,了解CL-20/GAP推进剂的热分解性能和推进剂的细观形貌。LI等[9]利用分子动力学方法研究了RDX/GAP推进剂的结合能、力学和能量性能等,并最终建立了结构-性能关系。SONG等[10]依据GAP弹性体与应变速率和温度相关的力学性能,构建了考虑时间、温度的GAP本构方程,通过实验与计算结果对比发现两者基本一致。ZHANG等[11]研究了GAP/CL-20/HMX推进剂在单轴拉伸下的应力-应变曲线,并建立了该推进剂的本构模型。以上研究主要对GAP基推进剂从细观角度进行研究,而对于该类推进剂的损伤本构研究相对较少。国内外对于复合推进剂的本构的研究工作主要集中在宏观及细观两方面。宏观方面对推进剂的拉伸应力应变响应进行综合分析,并引入软化函数或损伤因子来表述推进剂的非线性行为。SCHARPERY[12]基于热力学分析推导了利用内变量来表示推进剂损伤的非线性本构。众多学者在此基础上对推进剂的非线性本构进行了深入研究与发展。细观方面则主要是对推进剂的细观损伤演化进行模拟分析,考察其损伤演化过程中的某一损伤量对力学性能的影响。XU等[13]考虑了推进剂细观结构损伤如空洞和颗粒/基体界面脱湿在外载作用下的变化情况,构建了三维非线性粘弹性本构。刘承武等[14]基于Weibull统计学方程推导出了复合固体推进剂在不同方向开裂下的非线性粘弹性本构方程。徐强等[15]通过建立与应变率相关的损伤函数来构建可以描述NEPE推进剂拉伸损伤变化的非线性粘弹性损伤本构。从以上研究可以看出,无论在宏观方面还是细观方面都能通过构建本构来描述推进剂的力学行为。本文的HEDM(High-energy-density matter)推进剂中包含AP、CL-20、HMX这三种氧化剂颗粒,该推进剂的宏细观力学性能在这些不同氧化剂颗粒的影响下明显异于其他推进剂。因此,需要根据HEDM推进剂的力学行为构建合适的损伤本构。
本文主要从宏细观角度研究了HEDM推进剂的力学性能,该推进剂主要由GAP粘合剂、HMX、CL-20和AP颗粒以及铝粉等组成。首先,基于粘弹本构理论对HEDM推进剂的非线性本构进行了推导;其次,结合单轴拉伸实验以及应力松弛实验结果,分析了HEDM推进剂在单轴拉伸作用下的损伤演化规律,得到了HEDM推进剂的非线性粘弹本构,该本构主要适用于常温下宽泛应变率的推进剂力学性能描述,因为暂时缺乏不同温度条件下HEDM推进剂力学性能拉伸试验参数,该本构不能描述不同温度下的推进剂力学性能;最后,结合HEDM推进剂的颗粒级配信息基于随机算法生成了该推进剂的细观代表性体积单元(Representative volume element,RVE)模型,分析了推进剂的细观损伤演化情况,将模拟所得的推进剂应力-应变曲线与构建的非线性本构方程曲线以及实验曲线进行综合对比,本文建立的非线性本构能较好地描述HEDM推进剂的力学性能。
1 非线性本构方程建立
推进剂作为一种多相的复合材料,其力学性能表现为粘弹性,假设固体推进剂没有损伤,其力学性能满足Boltzmann叠加原理,线性粘弹性模型可以写成积分形式:
(1)
其中,E(t)为松弛模量,多用Prony级数表示:
(2)
式中E∞为平衡模量,MPa;Ei为第i项弹簧元件的模量,MPa;τi为第i项松弛时间,s。
根据文献[15]可知,可使用应变率与参考应变率的比值外加一个材料参数a对松弛模量进行修正。此时,修正后的松弛模量满足:
(3)
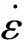
此时:
(4)
实际上推进剂因为外部载荷作用,其内部结构的损伤累计会导致推进剂的力学性能呈现非线性,通常用含有损伤内变量的软化函数来表示推进剂的损伤。此时,考虑推进剂模型的软化函数为C(S),对于非线性粘弹本构满足:
σnon(t)=C(S)σs(t)
(5)
其中
C(S)=1-S
(6)
式中S为损伤内变量,是表征材料内部损伤程度的物理量,宏观角度通常可用推进剂的实验所得的非线性粘弹应力值与线粘弹性应力响应相比。
最后,可用式(7)来表示损伤:
(7)
式中σs为实验应力值;σlin为线粘弹应力值。
推进剂作为一种典型的高填充的颗粒增强材料,在外载荷作用下,推进剂的内部损伤满足统计分布理论,假设细观损伤演化服从Weibull分布函数[16]:
(8)
式中m1和k1均为材料常数;εc为推进剂损伤开始的临界应变。
通过式(4)、式(5)、式(8)最终得到的非线性本构表达式:
(9)
2 本构方程参数确定
2.1 推进剂拉伸与松弛实验
为获得HEDM推进剂的力学行为,从而利用构建的非线性本构对其进行表征,开展了HEDM推进剂的拉伸与松弛实验。将HEDM推进剂的拉伸试件制作成标准哑铃型试件,根据《复合固体推进剂单向拉伸试验方法》QJ 924—85[17],保持室温条件,设定拉伸速率分别为2、10、20、50、100 mm/min时进行单轴拉伸试验,相对应的应变率分别为0.000 6、0.002 7、0.005 6、0.013 9、0.027 8 s-1。
HEDM推进剂单轴拉伸所得应力-应变曲线如图1所示。由图1可以看出,HEDM推进剂出现明显的双折线现象。当HEDM推进剂变形较小时,推进剂的应力-应变响应服从线粘弹性规律。这是因为初期载荷较小时,氧化剂颗粒的存在对基体的聚合物分子链的拉直活动进行了阻碍,从而使推进剂的模量得到一定的增强;当推进剂变形到一定值时,推进剂应力-应变响应出现明显的拐点,之后应力-应变曲线仍大致为线性变化。这是因为基体与颗粒之间界面慢慢开始脱粘,同时基体内部空洞、微裂纹等细观损伤进一步发生扩展,此时推进剂的承载能力减弱,但仍能承受一定载荷;最终当试件拉到断裂强度时,推进剂失效断裂。同时,由图1还可知,HEDM推进剂的应力随着应变率增大而增大,说明应变率越大推进剂的承载能力越强,该推进剂的应力-变化与应变率相关。因此,HEDM推进剂具有粘弹性。另外,拉伸速率越大,HEDM推进剂的断裂强度和断裂伸长率越大。
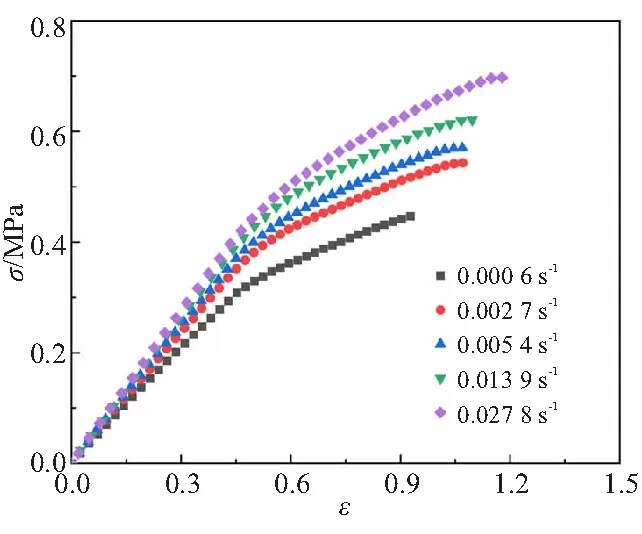
图1 不同应变率下HEDM推进剂的应力-应变曲线
为了得到HEDM推进剂的松弛模量E(t),根据《复合固体推进剂单向拉伸应力松弛模量及其主曲线测定方法》QJ 2487[18]对推进剂试件进行应力松弛试验,设定初始拉伸速率为100 mm/min,初始恒定应变为 5%,松弛时间为1000 s。最终获得4组有效试验结果,将其取平均值。对推进剂试验结果的平均值进行Prony级数拟合,拟合结果见图2。得到推进剂的松弛模量曲线方程各参数如表 1 所示。
从图2中可以看出,HEDM推进剂的松弛模量在短时间内迅速降低,之后逐步趋于稳定值,同时拟合的Prony级数所得到的计算结果与实验结果吻合良好。
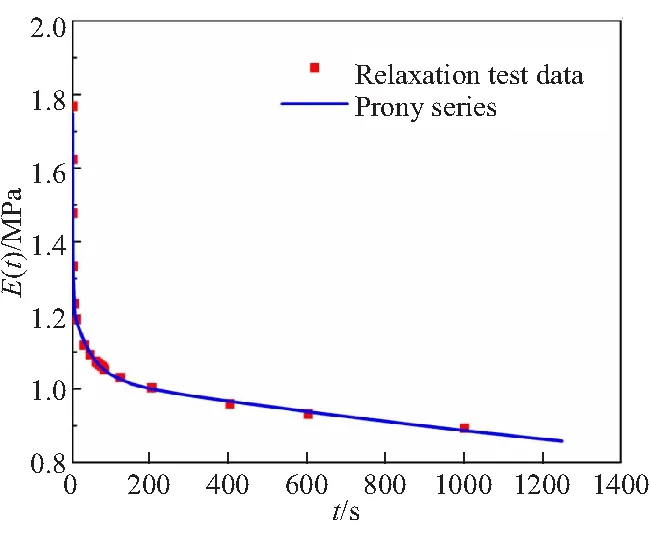
图2 拟合的松弛模量曲线与实验对比图
2.2 本构参数拟合
将图1应变率为0.000 6、0.002 7、0.005 6、0.013 9 s-1的4条曲线用来建立各系数表达式。参考文献[15],为得到修正松弛模量,对4种不同应变率的单轴拉伸应力-应变曲线的未损伤部分进行拟合得到:
(10)
HEDM推进剂中含有大量的随机分布的氧化剂颗粒,而推进剂的损伤断裂在细观角度来看是因为推进剂基体与颗粒界面较为薄弱,在外载荷作用下,颗粒/基体界面大量脱湿,之后推进剂基体内部微裂纹进一步扩展形成空洞,推进剂的承载能力降低,最终推进剂失效断裂。推进剂的固体颗粒分布随机,此时假定推进剂的损伤也随机产生且损伤分布满足统计学的理论,依据Weibull分布法则,对4种应变率下的损伤量进行表征,可得到不同应变下的相关参数,见表2。将2个材料参数进行拟合,得到表达式如式(11)所示。

表2 不同应变率下的式(7)的相关系数值
根据实验可知,推进剂在不同应变率下的临界损伤应变值为εc=0.45。最终将式(10)、式(11)代入式(9),得到了HEDM推进剂的非线性本构。
为验证建立的含损伤的非线性粘弹性本构方程的有效性,将应变率0.000 6、0.002 7、0.005 6、0.013 9 s-1代入建立的非线性本构进行计算,同时对拉伸速率为0.027 8 s-1的推进剂应力-应变响应进行理论预测,并与5组应变率下的实验结果进行对比分析,得到实验与预测的结果如图3所示。
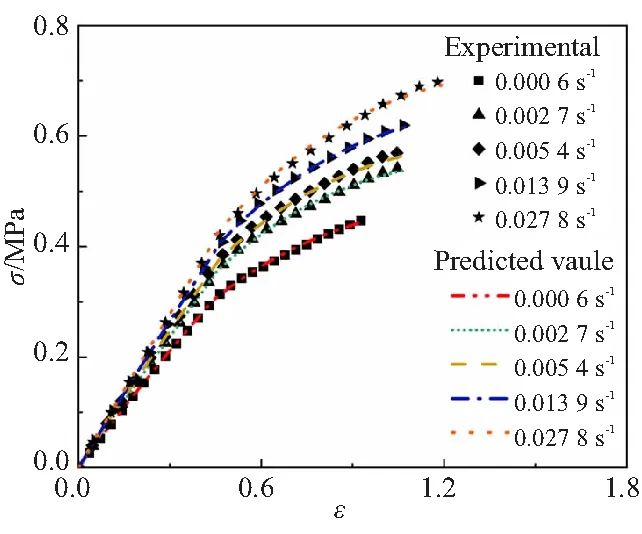
图3 HEDM推进剂的实验与预测结果
为了考察实验值与预测结果的误差情况,根据提出的非线性本构分别计算5组应变率下理论值与实验值间的相对标准偏差(RSD),计算结果见表3所示。
(12)
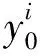
从图3、表3的结果可以看出,建立的含有损伤的非线性粘弹性本构方程能较好地预测HEDM推进剂整体的应力-应变关系。在推进剂未损伤时,理论值与实验值基本趋于一致,且每组应变率下的总体误差不超过10%,该非线性本构能较好地描述该推进剂的力学性能。该本构主要适用于常温下宽泛应变率的推进剂力学性能描述,因为暂时缺乏不同温度条件下HEDM推进剂力学性能拉伸试验参数,该本构不能描述不同温度下的推进剂力学性能。
3 HEDM推进剂细观损伤演化
由于固体火箭发动机在生产、贮存以及使用过程中会承受各种复杂载荷,推进剂的失效机理也比较复杂。HEDM推进剂是以GAP为基体并包含大量固体颗粒的含能材料,其力学性能受载荷速率的影响也比较明显。在载荷持续作用下,基体与固体颗粒之间的粘接性能会随时间逐渐改变,从而引起推进剂宏观力学性能的变化。因此,对推进剂的细观损伤过程的探究,可以一定程度上表征推进剂的宏观力学性能失效机理。
3.1 HEDM推进剂细观建模
依据表4 HEDM推进剂的组分信息生成的推进剂在微CT观测下的推进剂的细观结构(如图4所示)。根据生成HEDM推进剂的配方级配信息,将推进剂氧化剂颗粒简化为球形,并结合生产颗粒在基体中随机分布的特点,基于顺序填充算法生成的RVE模型如图5所示。
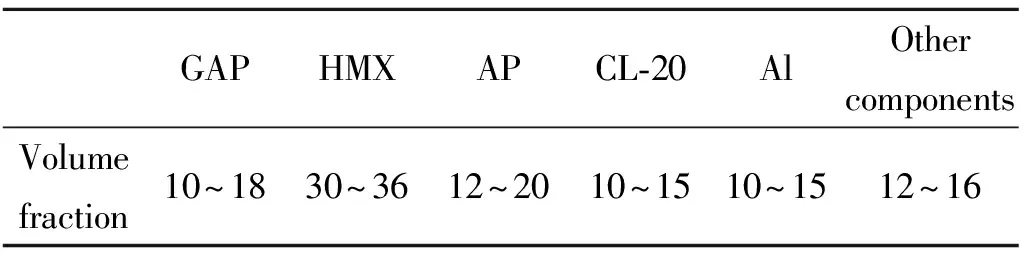
表4 HEDM推进剂的组分信息
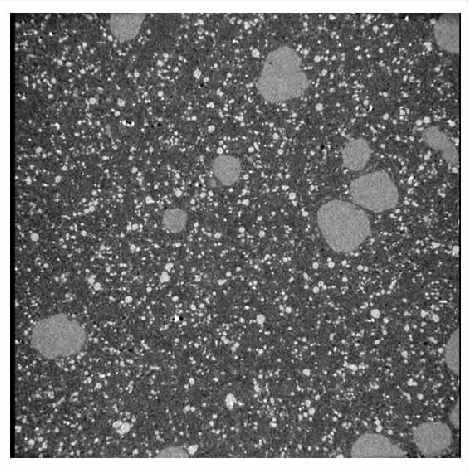
图4 HEDM推进剂的细观结构
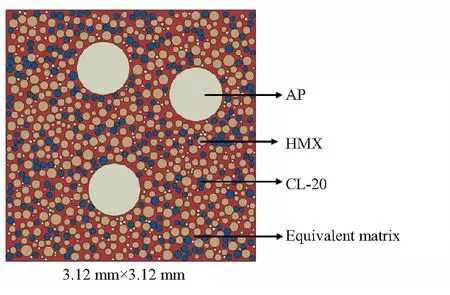
图5 HEDM推进剂的RVE 模型
该算法生成推进剂细观模型方便快捷,且由于HEDM推进剂不考虑Al粉后的总体固含量在57%左右,该算法便能满足HEDM推进剂RVE模型的建立。根据文献[19]建立的RVE模型应大于最大尺寸颗粒的3~5倍,本文建立的RVE模型尺寸可以满足要求。
GAP基体具备粘弹性材料的基本性质,属于橡胶材料范围,是导致固体推进剂具有粘弹性的根本原因。因此,在计算过程中要充分考虑固体推进剂基体的材料特性。GAP的材料参数可以参考文献[10],将基体和Al粉采用文献[20]的方法进行等效,从而得到等效基体的松弛模量,如表5所示。同时将HMX、CL-20和AP氧化剂颗粒均视为线弹性体,其材料参数如表6所示。
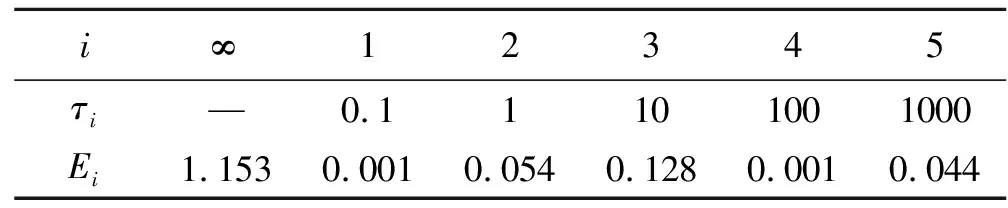
表5 等效基体松弛模量 Prony 级数的系数
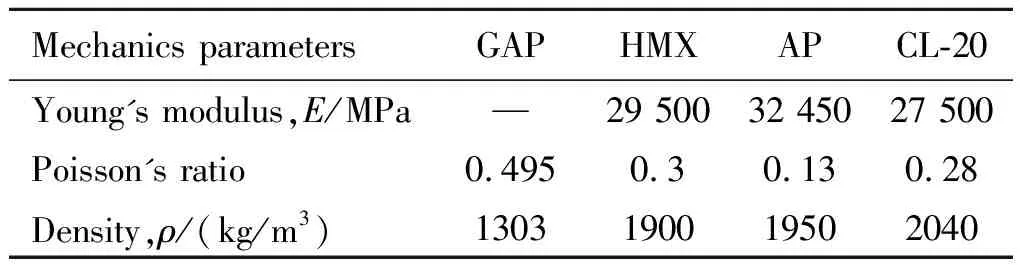
表6 HEDM推进剂各组分力学参数
3.2 内聚力参数确定
推进剂基体与颗粒间存在明显的界面,众多学者也将内聚力模型引入推进剂颗粒/基体界面进行推进剂的细观损伤断裂过程模拟,该方法能准确表征推进剂在单轴拉伸过程中基体与界面的脱湿和基体内部断裂全过程,从而有效实现对推进剂细观损伤机理探究。
双线性内聚力法则是在损伤失效模拟研究中采用较多更为通用的法则,也多用于推进剂细观损伤演化过程,可以用式(13)的关系式来表示。
(13)
在ABAQUS中多用刚度衰减率(SDEG)来检测材料是否损伤失效。其中,当SDEG=0时表示材料没有损伤,SDEG=1时表示材料已经完全损坏。实际材料破坏到SDEG=1时难度较大,此时可以假定SDEG= 0.99时材料已经完全失效破坏。
在颗粒/基体界面,以及基体内部网格间均插入Cohesive网格单元,插入结果如图6所示。

(a)Cohesive elements at the particle/matrix interface (b)Cohesive elements inside the matrix
双线型内聚力模型主要与界面断裂强度,刚度系数以及特征位移三个系数相关。取切向与法向的界面参数一致,采用Hooke-Jeeves反演算法,可以实现对颗粒/基体界面以及基体间的内聚力模型参数获取参考文献[21]。获取的参数见表7所示。

表7 颗粒/基体界面以及基体间的内聚力模型参数
3.3 HEDM推进剂细观演化分析
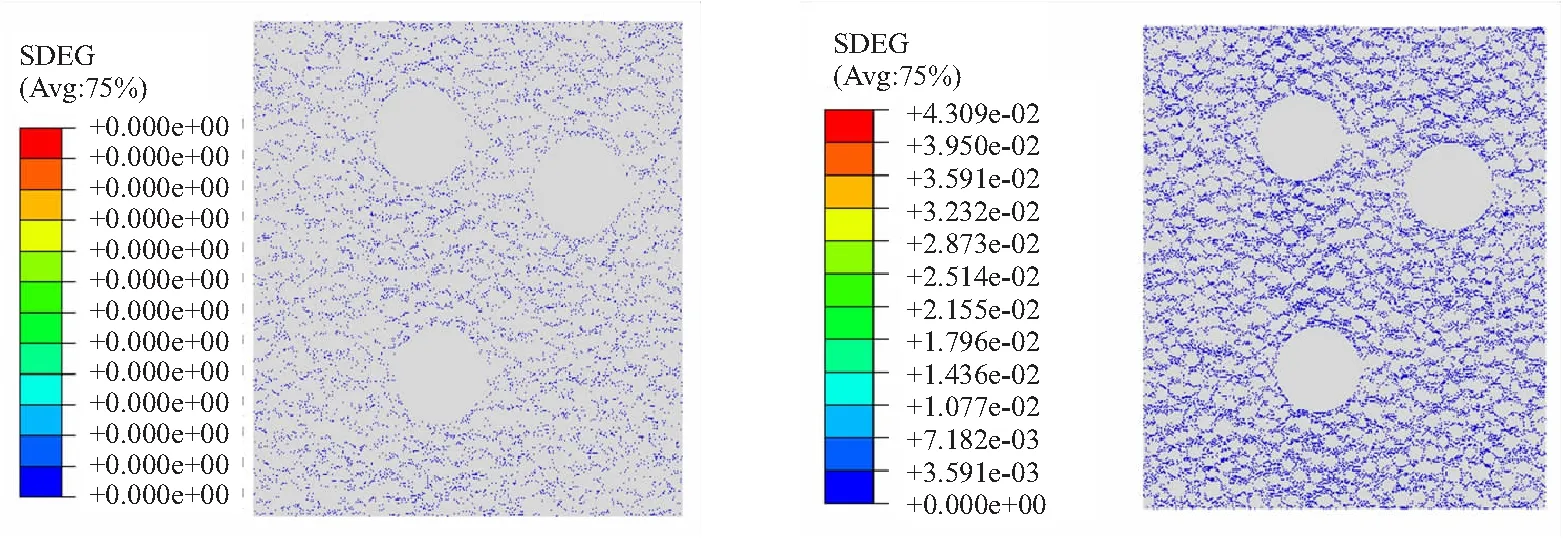
以拉伸速率为2 mm/min(应变率0.000 6 s-1)进行拉伸模拟,HEDM推进剂细观结构在拉伸过程中在应变分别为4.82%、18.75%、45.19%、99.13%的SDEG变化如图7所示。将上面4个应变对应在仿真模拟的应力-应变曲线中的A、B、C、D各点如图8所示。
(a)ε=4.82% (b)ε=18.75%
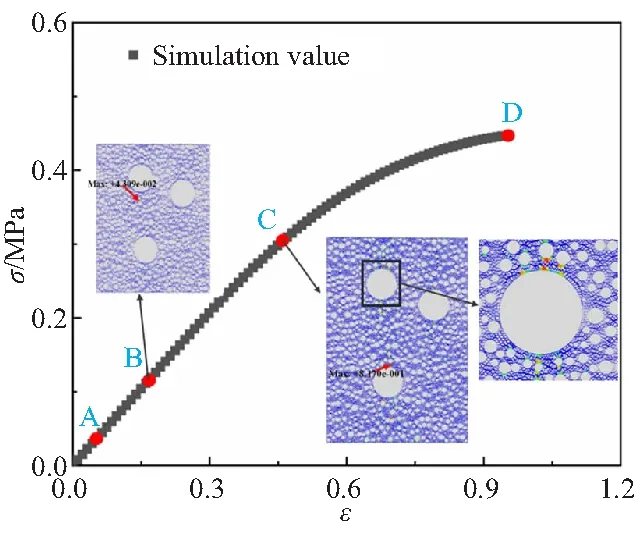
图8 0.000 6 s-1应变率下的仿真应力-应变曲线
从图7和图8中可以得出,HEDM推进剂细观损伤直至断裂的演化过程。在应变率为0.000 6 s-1的单轴拉伸过程中,当初始应变较小时,此时推进剂内部没有损伤,应力-应变曲线为线性变化;当应变为18.75%时基体内部小颗粒周围出现损伤,此时基体内部损伤对推进剂应力变化规律影响忽略不计,推进剂应力-应变曲线仍为线性变化。当应变为45.19%时,损伤开始出现于大颗粒周围以及密集颗粒附近,此时推进剂开始出现非线性变化,随着加载的进一步进行,大颗粒以及颗粒密集区域的颗粒/基体界面开始脱湿,基体内部开始损伤,此时的推进剂承载能力降低。最后,推进剂基体内部形成微裂纹并不断扩展联合,最终整个推进剂失效,此时推进剂的应变为99.13%。可以得出HEDM推进剂的细观破坏由粘合剂基体损伤、断裂以及GAP粘合剂与固体氧化剂颗粒之间的“脱湿”两种因素共同作用导致的,这与文献[22]所观测的GAP推进剂细观损伤演化规律基本一致。
将应变率为0.000 6 s-1的推进剂进行拉伸模拟得到应力-应变曲线与实验曲线进行对比如图9所示。其实验值与仿真值的误差为5.61%。可以看出仿真曲线与实验曲线在整体上较为一致。在推进剂未损伤时两曲线的重合度较高,而在推进剂损伤直至断裂部分两条曲线略有误差。可能是因为构建的仿真模型将氧化剂颗粒简化为球形,而实际的颗粒多为不规则形状,另外不同颗粒与基体间界面属性略有差异,从而导致该误差的存在。
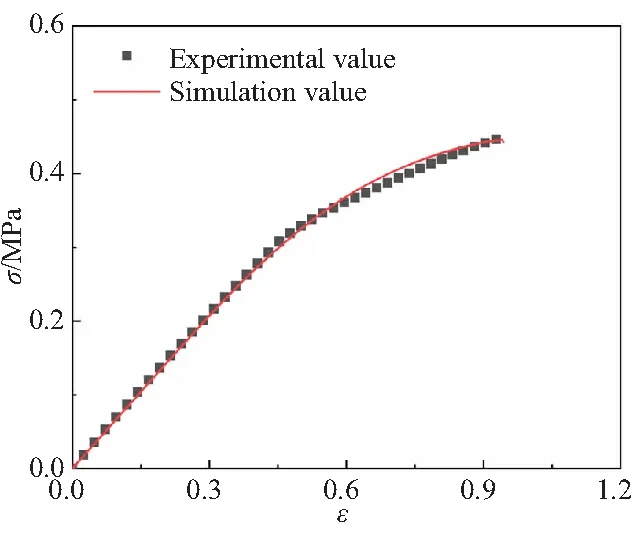
图9 应变率为0.000 6 s-1时的仿真与实验对比图
利用仿真分析对未进行实验的一组拉速进行模拟预测其仿真力学性能曲线,结合推导的非线性本构在该拉速下的理论曲线可以实现进一步验证推导的非线性本构的准确性。将拉伸速率为5 mm/min对应应变率为0.001 4 s-1的有非线性损伤本构理论推导出的应力-应变曲线与仿真模拟的推进剂应力-应变曲线进行分析,如图10所示。该应变率下的仿真值与理论值的误差为9.83%。从图10中可以看出,该非线性本构理论值在应变率为0.001 4 s-1时与仿真值一致性较高。因此,该非线性本构能较好地表征HEDM推进剂的力学性能。
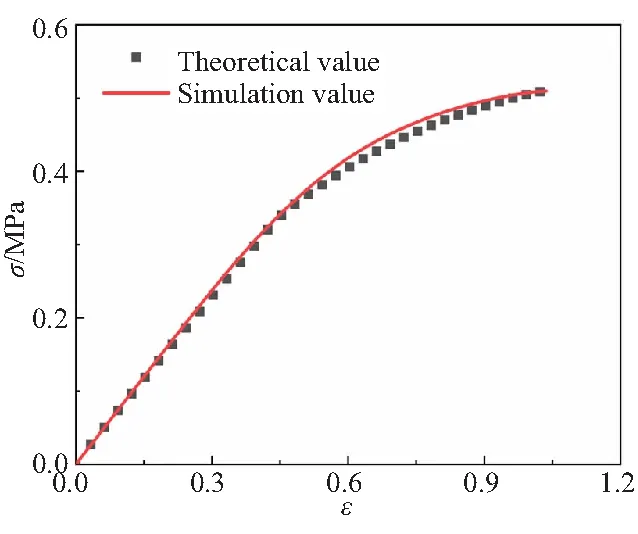
图10 应变率为0.001 4 s-1时的仿真与理论对比图
4 结论
(1)HEDM推进剂在单轴拉伸情况下应力-应变响应呈现明显的双折线变化。在应力变化的拐点之前呈线性变化,之后因为推进剂内部细观损伤的扩展导致推进剂失去一定的承载能力,但是应力-应变响应基本仍为线性变化,最终推进剂在外载荷的持续作用下失效断裂。且HEDM推进剂的应力-应变响应与拉伸速率相关,随着拉伸速率增大,推进剂承载能力增强,推进剂内部的损伤扩展对慢应变率更加敏感。
(2)假定推进剂细观损伤满足Weibull分布规律构建了HEDM推进剂的非线性本构。该非线性本构在一定程度上可以较好地描述该HEDM推进剂的力学性能。HEDM推进剂非线性本构的建立,可以为未来对HEDM推进剂药柱的结构完整性研究以及预估HEDM推进剂药柱的寿命方面提供一定的指导。
(3)通过对HEDM推进剂建立RVE模型,并引入内聚力法则,对HEDM推进剂的细观损伤演化进行分析,得到其在外载荷作用下的细观损伤机理如下:加载初期,推进剂损伤开始在小颗粒附近产生,此时的损伤对推进剂的受载情况影响不大,应力-应变曲线为线性变化;当进一步加载,推进剂内部大颗粒周围以及其他颗粒密集区出现大规模损伤时,推进剂的承载能力开始降低,此时推进剂的应力开始表现出非线性;之后,大颗粒与基体界面首先“脱湿”在小颗粒周围部分“脱湿”同时基体内部产生损伤,最终推进剂失效断裂。
