面向极端波浪模拟的圆形全向聚焦波合成算法与试验研究
2023-04-25倪艺萍王天奕郭泽斌
倪艺萍,王天奕,王 磊,林 俊,陈 俊,郭泽斌
(珠江水利委员会珠江水利科学研究院,广东 广州 510610)
极端聚焦波是多个波浪在运动中相互调制、叠加集中,而在某一特定时刻、地点形成的一个孤立大波,具有波高大、非线性强、能量集中、出没无常等特点,其波峰的速度远远大于同等波高的其他波浪,并且其运动和变形以及内部水动力形态都很复杂,对海洋结构物和船舶造成巨大威胁,是极端海况波浪模型试验的重要研究对象[1]。因此,分析聚焦波的产生机理、基本特性、演化过程及对建筑物的作用等,对海洋水动力学的发展具有十分重要的理论意义,对海洋船舶、钻井平台等工程结构的设计和防护具有不可或缺的实际意义[2]。
目前对聚焦波的研究多集中于数值模拟,试验研究尚少[3-4]。且现有波浪模拟算法多应用于常规港池(矩形),适用于近岸、浅海等海洋环境模拟,无法满足深海环境波浪模拟。区别于浅海波浪,深海区波浪全向作用于研究对象,因此深海波浪模拟需采用圆形波浪港池,波浪模拟装置也需360°布置。目前全球仅有3座圆形水池,分别是英国FloWave圆形水池[5 -6]、日本NMRI深水海洋工程水池[7]和日本AMOEBA圆形波浪水池[8],见图1、2,可在水池中模拟强非线性波。

图1 英国FloWave圆形波浪水池

图2 日本AMOEBA圆形波浪水池
1 聚焦波生成理论
聚焦波模拟是模拟奇异波恶劣海况的基础,较为真实的恶劣海况的模拟以聚焦波理论为基础。在本文中,根据聚焦波的形状不同,可将其分为单峰聚焦波、双峰聚焦波、偏心聚焦波、椭圆聚焦波、旋转聚焦波、图形类聚焦波(D形聚焦波、口字形聚焦波)等,单峰聚焦波在池中心处仅有一个波峰,双峰聚焦波在不同位置同时有2个波峰,偏心聚焦波在非池中心处仅有一个波峰,椭圆聚焦波的横截面为椭圆形,旋转聚焦波在水面上作旋转运动,图形类聚焦波在水面上呈特定形状。对聚焦波浪特性以及聚焦波产生方法进行研究可为进一步探究极限波浪奠定良好的基础。
聚焦波生成采用双叠加模型[9],考虑多频率不同方向波浪聚焦[10],其基本思路为:在空间与时间的某一固定点(聚焦点)处,所有组成波均以零相位叠加,从而在该点处形成一个极高的波峰,从分析这个叠加点出发,反推得到造波板的位移曲线。
由线性叠加理论,在任意点处波浪自由面可以表示为不同频率和不同方向的规则波叠加的结果,即[11]:
(1)
式中aij——频率为fi、方向角为θj的组成波波幅;ki——波数;φij——组成波初相位;Nf、Nθ——组成波频率数和方向数。
组成波频率ωi和波数ki满足线性色散关系。
(2)
式中 g——重力加速度;h——水深。
如果假定波浪在指定时刻t=tb时聚焦于位置 (xb,yb),即各组成波在该处叠加,要求:
cos(kixbcosθj+kiybsinθj-2πfitb-φij)=1
(3)
则各组成波的初相位应满足式(4):
φij=kixbcosθj+kiybsinθj-2πfitb+2mπ,m=0,±1,±2,…
(4)
将式(4) 代入式(1) ,并取m=0,这时可把波浪的波面η(x,y,t) 写成:
ki(y-yb)sinθj-2πfi(t-tb)]
(5)
即聚焦波浪的波面取决于波浪聚焦的位置和时间以及相应组成波的频率和方向分布等。假定分段式多向波造波机布置于x=0 m处,由线性造波理论,在水池中指定位置(xb,yb) 产生聚焦波,各造波板的运动可以写为:
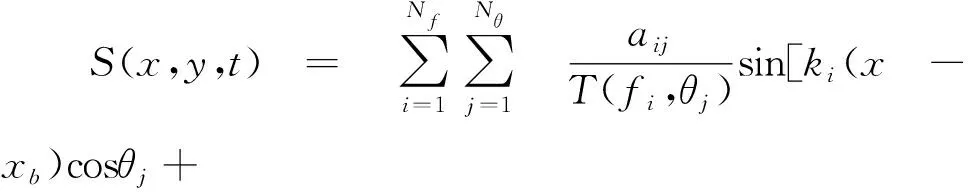
(6)
(7)
设波浪的聚焦波幅为A,是各组成波波幅之和:
(8)
式中T(fi,θj) ——分段式造波机的传递函数;aij——各组成波的波幅,取决于波浪的频谱分布形式,各组成波的能量均匀分布在[θmin,θmax]范围内。
另外,假定离散频率fi均匀分布在[f1,fn]频率范围内,定义频率区间宽度和中心频率分别为:
(9)
对于特定水深,指定位置(xb,yb)产生的聚焦波浪的波面特性主要取决于中心频率、频率宽度、聚焦波高等。
2 圆形全向聚焦波合成算法
圆形全向聚焦波合成算法,该算法利用圆形港池造波机的独特对称性和造波板的相互配合,实现了单峰、双峰、偏心、旋转、图形类等多种聚焦波形的模拟生成,可为深海风暴、海啸、超强台风等极端海况引起的各种随机的、陡峭的、破坏力极强的聚焦波模拟提供技术支撑。下面以单峰聚焦波、偏心聚焦波、椭圆聚焦波为例,聚焦波算法运行流程示意见图3。
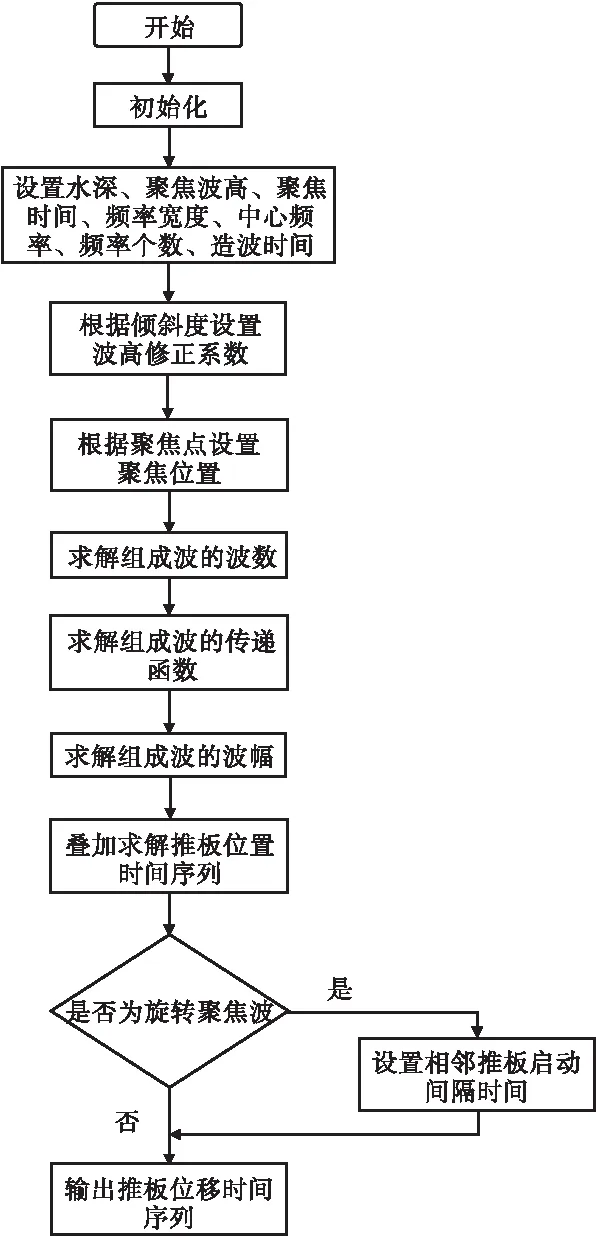
图3 聚焦波算法运行流程示意
2.1 单峰聚焦波
单峰聚焦波是位于圆心处的单一水柱,它具有360°对称性,所有造波板同步运动,所以圆形港池造波机只需考虑单块板的运动控制(即造波参数设置)。设置聚焦点位于圆形港池圆心处,聚焦位置为半径长度;设置合理的组成波频率宽度,使得组成波的频率变化范围更广,聚焦效率更高,适应性更强;设置合理的中心频率,使主要频率向低频靠拢,增加低频组成波的占比,可使得聚焦效果更明显。
在圆形港池中,以32个圆形造波机单元为例,将32块造波板进行编号,建立笛卡尔坐标系,原点为水池中心,x轴正向指向1号造波板,目标聚集位置表示为(xb,yb) ,见图4,计算点(xb,yb) 与每块造波板间的距离作为各自的聚焦位置,即圆池半径。
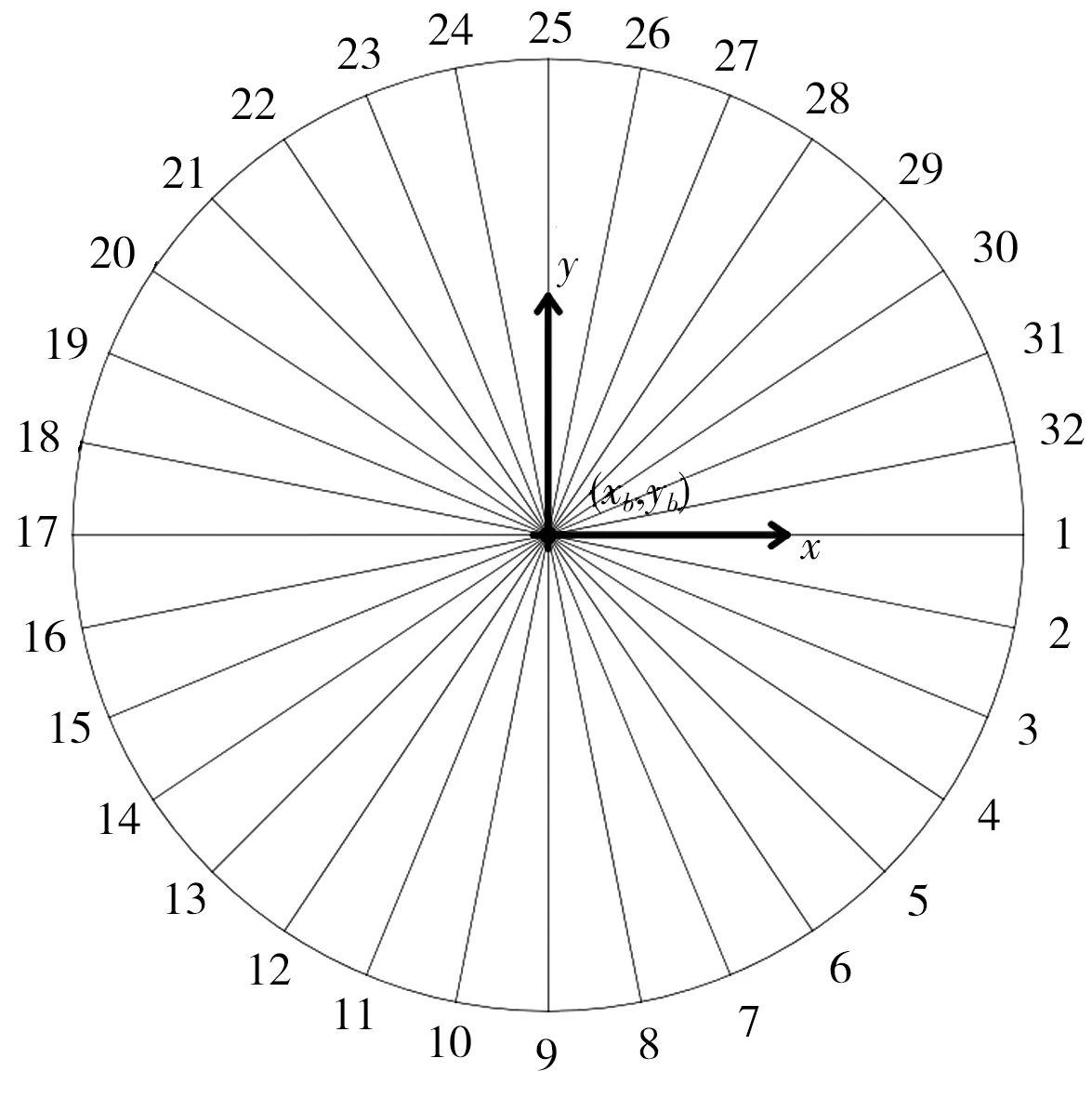
图4 参考坐标系下的单峰聚焦波
2.2 偏心聚焦波
偏心聚焦波是在圆池中非中心处生成单独的水柱,见图5,偏心聚焦情况下,圆形水池中所有板的聚焦位置、聚焦波高有所不同,其余参数均相同。由于偏心使得靠近聚焦点附近的小部分造波板(呈小扇形分布)产生的波浪场能量强,而远离聚焦点的大部分造波板(呈大扇形分布)产生的波浪场能量弱,这导致2个区域的生成波浪在到达聚焦点处聚焦时,聚焦水柱向能量弱的大扇形造波板方向倾斜。因此需要对部分造波板的聚焦波高做修正,使2个区域的波浪场能量大致相同,保证水柱垂直。
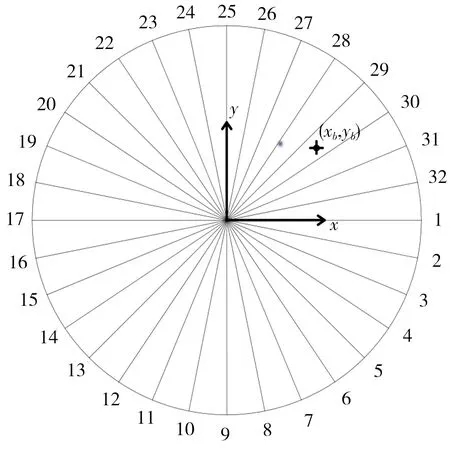
图5 参考坐标系下的偏心聚焦波
对圆形港池中距离聚焦点最远的那一块或两块造波板的聚焦波高乘以某个大于1的修正系数,其余造波板按照远离该造波板的顺序依次线性递减至1,此时,所有造波板的聚焦波高均包含有一个大于等于1的修正系数,如此,圆形港池中波浪场的能量均匀分布,产生的偏心聚焦水柱也垂直而上,定义此时最大的修正系数为临界修正系数。
或者亦采用延时聚焦的方法,使得靠近聚焦点的小扇形造波板在原来的聚焦时间的基础上,延长聚焦时间,同样可以实现垂直聚焦的效果。本文采用的是第一种方法。
设置聚焦波高修正系数的方法也可以用于控制聚焦水柱的倾斜度。在临界修正系数的基础上,设置修正系数小于该临界修正系数,则聚焦水柱向圆池外倾斜,若修正系数大于该临界修正系数,则水柱向圆池内倾斜,由此,可控制聚焦水柱的倾斜方向及角度。
2.3 椭圆聚焦波
椭圆聚焦波是在圆池中心或非中心处生成的横截面为椭圆形状的单一水柱,椭圆聚焦情况下,圆形水池中所有板的聚焦位置设置不同,其余参数均相同。将圆形造波机划分为4组,根据造波板所处区域的不同设置不同的聚焦位置。以32个圆形造波机单元为例,将32块造波板分区成四部分:第1—6、28—32块造波板为一区,第7—11块造波板为二区,第12—22块造波板为三区,第23—27块造波板为四区,见图6。椭圆曲线与32块板中垂线的交点即为各个造波板的聚焦点,根据椭圆的长轴设置一区和三区造波板的聚焦位置,根据椭圆的短轴设置二区和四区造波板的聚焦位置。由此,聚焦形成的水柱横截面呈椭圆的形状,且椭圆的长短轴可根据聚焦位置的设定而变化。
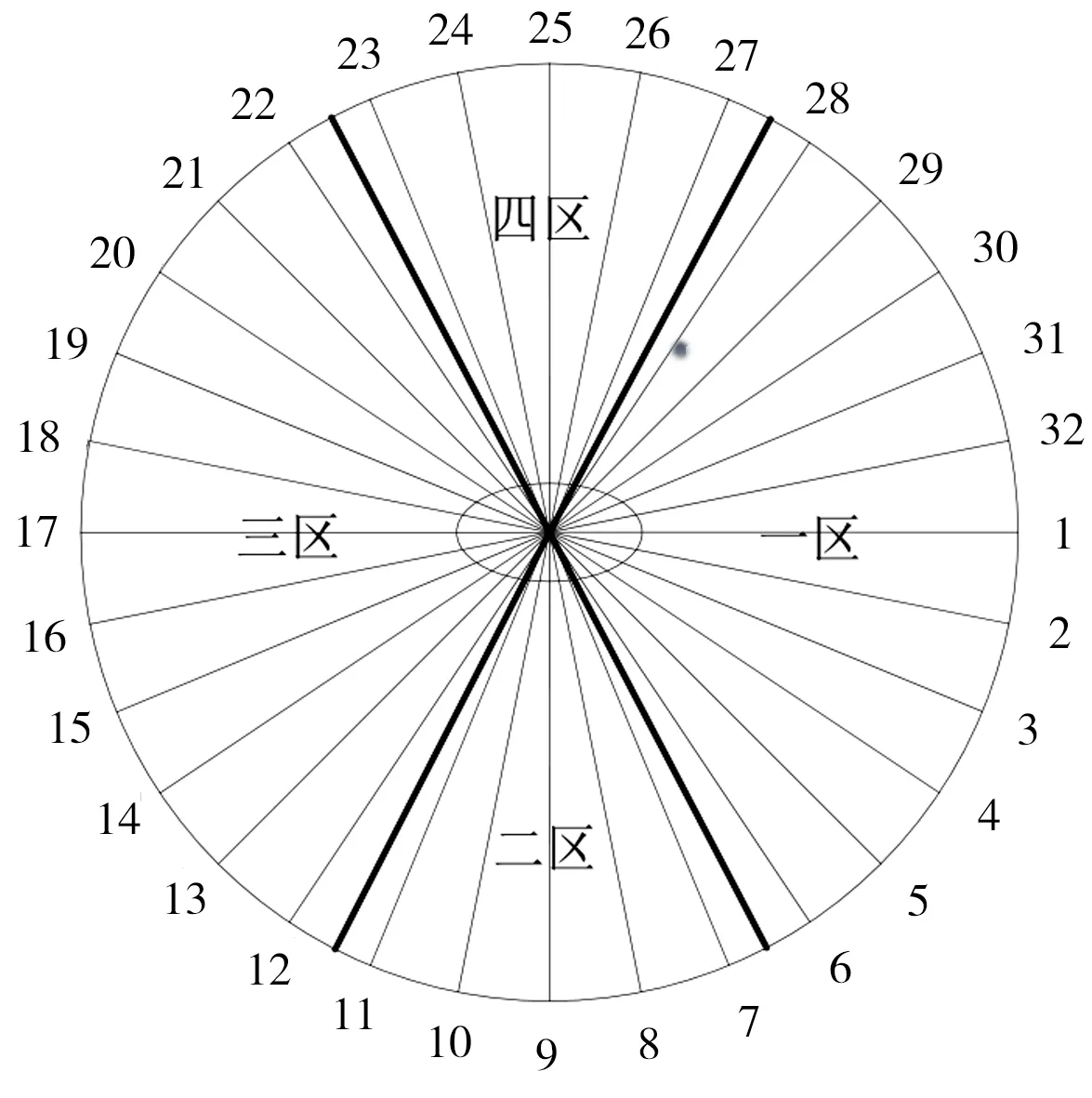
图6 圆形港池分区示意
3 试验条件
本次试验所用的圆形港池是珠江水利委员会珠江水利科学研究院自主研发的国内首座圆形港池[12],见图7,港池造波系统最大直径5 m,造波机位于零位形成的圆池半径值2.17 m,最大工作水深0.3 m,32个推板式造波单元在圆形水池壁上环绕布置,单板宽度为0.5 m,每个造波单元设有独立的电机控制。造波机采用钢框架结构,具有较好的强度和刚度,推波板采用不锈钢薄板,具有较好的韧性,运动机构采用精密线性导轨及滚珠丝杠,保证定位精度及重复精度。港池底部标有20 cm×20 cm的网格,用于波浪位置及其尺寸的确定。

图7 圆形港池
表1为试验聚焦波参数。试验包括3种类型的聚焦波——单峰聚焦波、偏心聚焦波和椭圆聚焦波,单峰聚焦波有4种:上冲射流、直径5 cm的水晶柱、直径20 cm的水晶柱、“梦笔生花”,偏心聚焦波有3种:垂直偏心聚焦波、外倾80°偏心聚焦波、内倾80°偏心聚焦波,椭圆聚焦波有3种:短轴为8 cm,长轴分别为20、40、60 cm的椭圆聚焦波,考虑的参数设置主要有聚焦波幅、中心频率、频率宽度、造波时间、聚焦时间、聚焦位置、波高系数等。
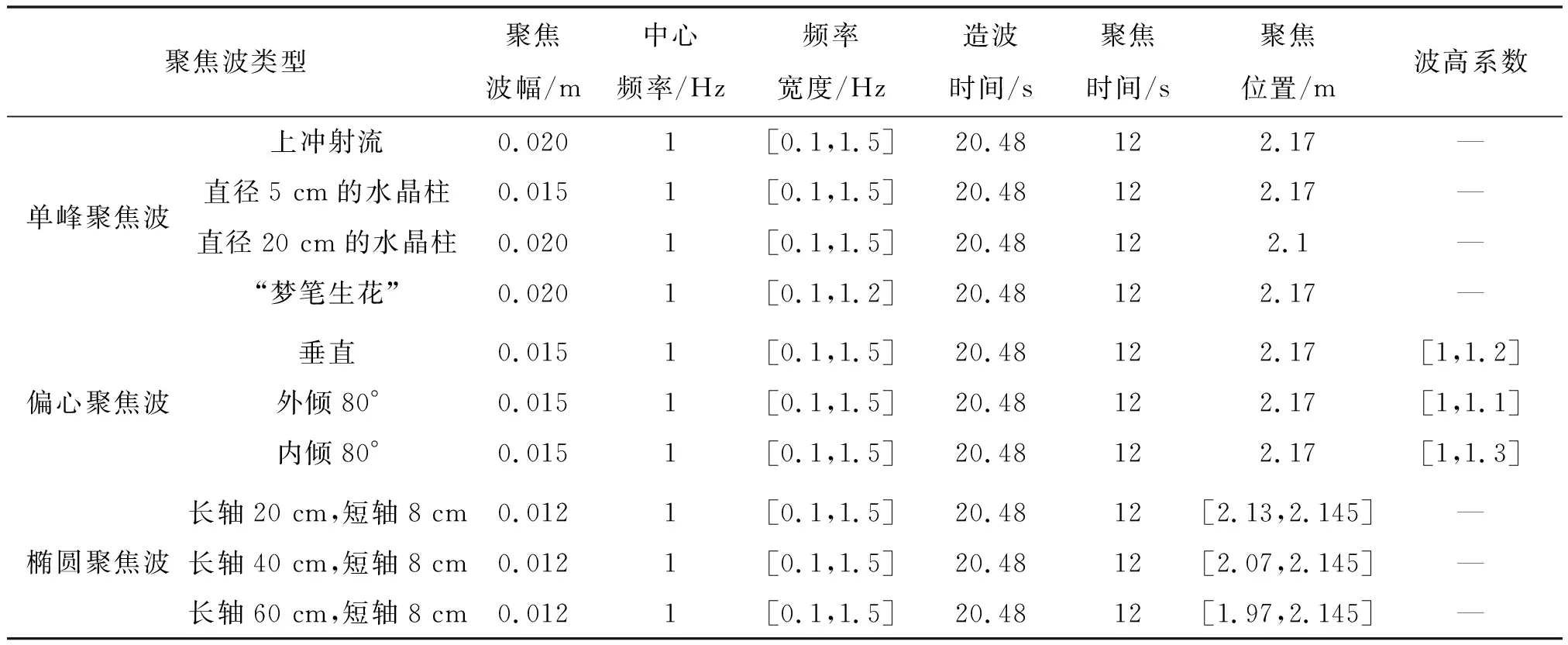
表1 试验参数
单峰聚焦波单块造波板的运动曲线见图8a,对于偏心聚焦波和椭圆聚焦波,由于每一块造波板的聚焦高度设置不同,所以其运动曲线不同,举例1号造波板的运动曲线见图8b、8c。
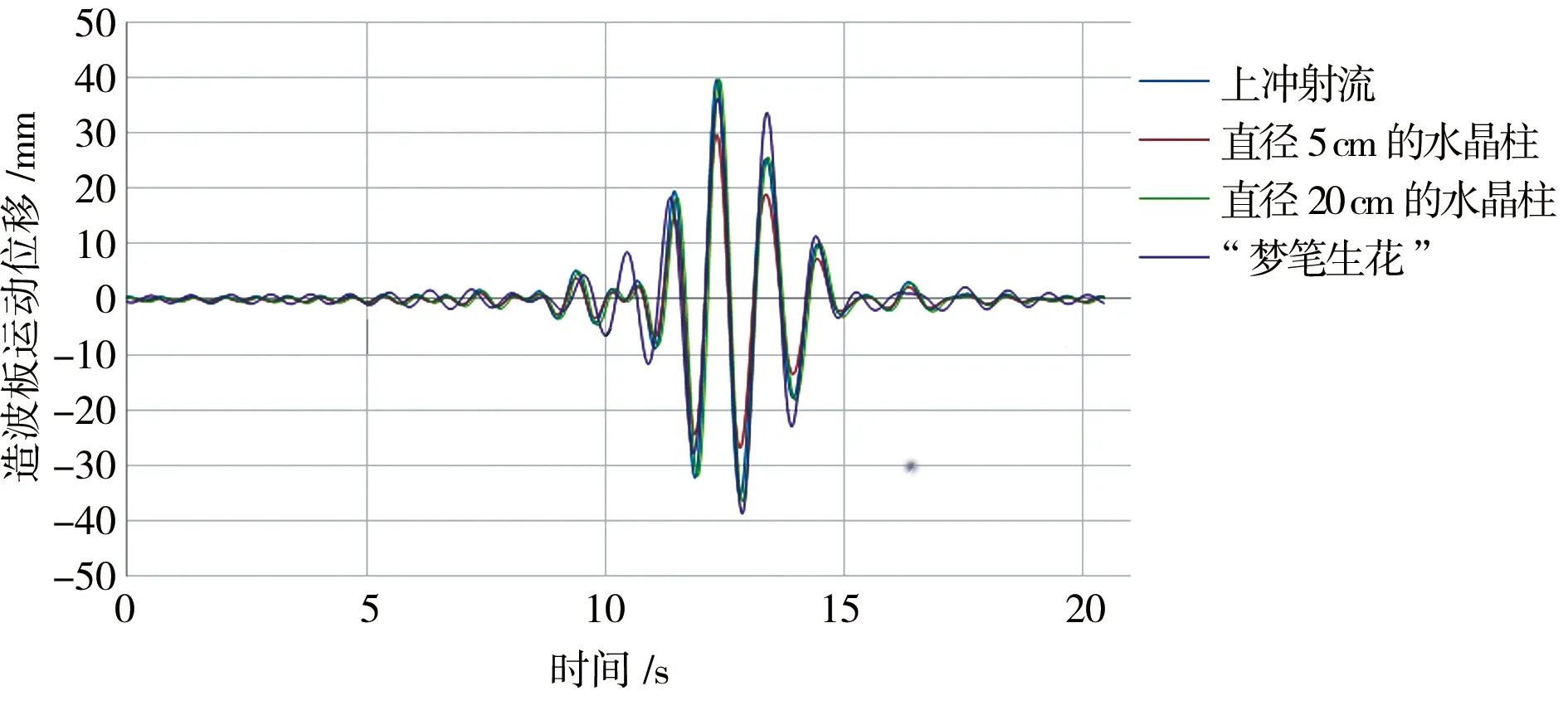
a)单峰聚焦波
4 试验结果
4.1 单峰聚焦波
在0.3 m水深条件下,利用聚焦原理可合成高达10 m的单峰聚焦波,射流放大比例超过30倍(波高与水深之比),能量极强、冲速极高,这是一种强非线性现象[11],单峰聚焦波上冲射流的演变历程见图9。在射流演变初期表现为上冲的光滑水柱,5 m时水柱上部开始出现射流,7.5 m时射流明显,最终射流达到9.7 m时完全破碎,上冲射流的形成是一个高度非线性的现象,这说明造波过程得到了很好的控制,并且造波质量极高。该射流可满足深水油气钻井平台、海上风机、船舶等结构可靠度及倾覆风险的模型试验研究需求。
4.2 粗细可控的单峰聚焦波
图10a中,细水晶柱设置直径为5 cm,水晶柱光滑连续不破碎,形同一根垂直向上的细针,也可以增加直径,生成直径20 cm的粗水晶柱,见图10b。
在这个过程中,通过不同组合的试验还模拟出了一种奇特的波形,图10c,形同朝上的毛笔尖,它的水柱底部连续光滑均匀,顶部发生扩散,由一维变为平面二维,这是由多种聚焦波合成产生,与水晶柱或射流的生成原理均不同。这是由于在聚焦前的一个凸起波叠加生成了具有一定小波高的合成波,该合成波运动至波谷处,恰好与传播至池中心的聚焦波相遇,还未消散的合成波被聚焦波向上托起,导致该合成波水平扩散开来,由此形成“梦笔生花”的形状。

a)2 m
4.3 垂直度可控的偏心聚焦波
利用圆形全向聚焦波合成算法可实现聚焦波空间姿态控制,可在池中任意位置(池中心或非中心)处产生聚焦,且可以控制聚焦水柱在±90°范围内发生倾斜。目标精准,指哪打哪,可用于水池中任意位置物理模型的聚焦波砰击试验[12],这在矩形港池中是很难实现的。如图11,在一固定位置处分别生成垂直偏心聚焦波、外倾80°偏心聚焦波、内倾80°偏心聚焦波。
4.4 长短轴可控的椭圆聚焦波
多数情况下聚焦波截面为圆形,是对称的,但实际海洋中,波浪形态万般变化,多是非对称的。针对这个特点,利用圆形全向聚焦波合成算法实现了聚焦波形的x、y轴非对称控制,模拟了不同长轴的椭圆聚焦波,可根据试验要求精准控制波形截面。
图12a椭圆长轴设定为20 cm,短轴8 cm,从图中可以看到长轴宽度占据一个网格,短轴宽度占据不到一个网格,与设定值相符,图12b椭圆长轴设定为40 cm,实际宽度占据2个网格,短轴占据不到一个网格,图12c设定为60 cm,实际宽度占据3个网格,短轴宽度占据不到一个网格,均都严格符合设定值。但当长轴为60 cm时,聚焦波上部发生扩散,这说明椭圆聚焦波长短轴设置有上限,达到一定限值后波形发散、能量发散。
4.5 其他波形
除了上述波形,通过圆形全向聚焦波合成算法还模拟生成了双峰聚焦波、D形聚焦波、旋转波、驻波等,见图13。

a)垂直偏心聚焦波

a)长轴20 cm、短轴8 cm的椭圆聚焦波

a)双峰聚焦波
5 结论
在圆形港池中,利用圆形全向聚焦波合成算法,可对聚焦波的位置、高度、直径、垂直度等波浪形态实现精准控制,成功模拟生成了粗细可控的单峰聚焦波、垂直度可控的偏心聚焦波、长短轴可控的椭圆聚焦波,准确性好且重复性高,满足科学试验对于真实极端恶劣海洋环境的模拟精准度需求。另外,通过圆形全向聚焦波合成算法还成功模拟了双峰聚焦波、旋转聚焦波、图形类聚焦波等多种聚焦波形,聚焦形态多样,亦可模拟矩形港池中的常规波形,如正弦波、驻波等,满足传统波浪试验的需求。
接下来,将进一步研究参数设置与波浪形态控制的数值化关系,另外,考虑圆度、陡度等波浪形态与聚焦波参数的关系,致力于利用圆形波浪港池和全向聚焦波合成技术模拟几乎所有极端波浪条件,以实现深远海区域复杂海况环境模拟。
