基于多源时间序列的滑坡位移动态预测
2023-04-25南骁聪刘俊峰张永选王育奎
南骁聪,刘俊峰,张永选,王育奎
(1.山东高速工程检测有限公司 山东省高速公路技术和安全评估重点实验室,山东 济南 250000;2.成都理工大学 计算机与网络安全学院,四川 成都 610000;3.山东高速烟台发展有限公司,山东 烟台 264000)
滑坡是中国最受关注的地质灾害之一。三峡库区建成之后,发生了多起滑坡。2014年9月1日,云阳县滑坡造成16人遇难,16人下落不明,28万民众受灾。2014年9月1日至5日,秭归县发生25处滑坡,造成348国道2处中断,一座水电站被完全冲毁。三峡库区的滑坡预警系统亟需建立,滑坡位移预测是其中的重要组成部分。
滑坡的演化过程是非线性的复杂过程,是多种因素相互作用的结果。滑坡位移的预测一般分为以下几个步骤:①分解总位移;②选择影响因子;③建立预测模型;④分析预测结果。趋势项主要由滑坡的前期位移趋势决定,周期项主要由影响因子决定。滑坡位移基本上由斜坡的势能和约束条件决定,但也受降雨和水库水位波动的强烈影响[1],因此选择降雨量和水库水位作为影响因子。
目前,滑坡预测的方法已经有了很大发展[2],包括基于物理模型试验[3]、统计理论、人工智能方法的研究[4]。对于应用于滑坡位移预测的人工智能方法,支持向量机(SVM)[5-6]、随机森林(RF)[7]、神经网络模型[8-9]、移动平均自回归模型[10-12]、极限学习机(ELM)[6,13]和 长短期记忆神经网络(LSTM)[14],极限学习机(ELM)的应用较多。部分方法将位移预测视为静态回归问题(如SVM,RF,XGBOOST)[15],然而,滑坡的位移通常是非线性和动态的,并且通常会受到时间相关因素的影响(如水库水位和降雨量)[16],考虑到滑坡位移影响因素的时间依赖性,可以采用动态预测方法。循环神经网络(RNN)已经广泛运用在滑坡位移预测[17],但存在长时依赖问题,该方法效果不佳。而采用长短期记忆神经网络(LSTM)[18],需要大量参数来构造循环网络,导致计算量增加和过拟合问题。Cho等[19]开发了一种全新的门控单元神经网络(GRU),可以解决长时依赖、计算量增加以及过拟合问题。
本文提出了一个混合机器学习模型,将二次指数平滑法(DES)和粒子群优化-极限学习机(PSO-ELM)结合起来,形成一种新型的人工神经网络结构,用于预测经常受到降雨和水库水位变化强烈影响的水库滑坡的位移。本文以具有阶梯状变形特征的太原市白家包滑坡为例进行研究,在对多源类型时间序列进行分解并充分了解该滑坡的变形机制的基础上,将与水库水位和降雨有关的6个主要影响因素输入预测模型,同时应用最小平方支持向量机(LSSVM)和卷积神经网络-门控递归单元(CNN-GRU)与PSO-ELM模型进行了比较,结果表明,PSO-ELM模型比其他2个模型具有更高的预测性能。
1 研究方法
1.1 趋势项和周期项
滑坡位移由2个分量组成:趋势位移和周期位移。趋势位移主要由地质构造、风化、岩性等条件控制。白家包的周期位移主要受降雨量和水库水位2个外部触发因素的影响[1]。累积位移时间序列可见式(1):
S(t)=φ(t)+η(t)
(1)
式中t——时间步长;S(t)——累积位移;φ(t)——趋势位移;η(t)——周期位移。
1.2 变分模态分解
变分模态分解是一种自适应、完全非递归的模态变分和信号处理的方法[20]。与传统的EMD和EEMD相比,VMD可以自行确定模态分解个数uk(k=1,…,K),将非线性时间序列分解,并进行重构,从而得到较为平滑的子序列,并且通过控制带宽来避免模态混淆,具有坚实的理论基础。
VMD总体是一个变分问题,主要包括该问题的构造和求解两部分。对于任何给定的信号f,变分问题使得每个模态的估计带宽和最小,并且满足uk之和等于原始信号f,因此求解问题可以表示为一个约束变分问题,见式(2):
(2)
式中f——原始信号;uk——第k个模态;K——需要分解的模态个数;ωk——uk的中心频率;δ(t)——狄拉克系数;* ——卷积运算符。
通过引入二次惩罚项和拉格朗日乘发算子,将该优化问题转化为无约束优化问题,得到的无约束问题见式(3):
L(uk,ωk,λ)=
(3)
式中α——二次惩罚因子;λ——拉格朗日乘数。
式(3)结合交替方向乘子迭代算法求解,更新后的uk、ωk、λ见式(4)—(6):
(4)
(5)
(6)
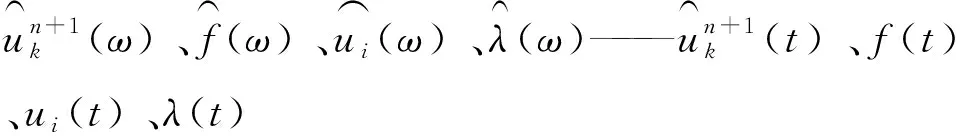
1.3 二次指数平滑法(DES)
指数平滑法是一种特殊的加权移动平均法[21]。一次指数平滑法适用于无趋势的时间序列的预测和分析,二次指数平滑法通常适用于呈线性变化的时间序列预测,见式(7)—(9):
si=ατi+(1-α)(si-1+bi-1)(0≤α≤1)
(7)
bi=γ(si-si-1)+(1-γ)bi-1(0≤γ≤1)
(8)
Ti+1=si+bi
(9)
式中si——当前数据τi在时间i时的平滑值;bi——时间i的最佳梯度估计;Ti+1——时间序列的一步超前预测。
1.4 粒子群优化算法(PSO)
粒子群优化(PSO)是一种优化算法[22]。它是由Eberhart和Kennedy提出的一种全局搜索算法,是一种模拟自然界中生物活动以及群体智慧的优化算法。粒子群优化算法利用群体中的个体共享信息,使整个群体的运动在解决问题的空间中从无序到有序地演变,从而获得最优解。
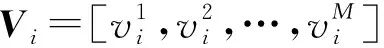
(10)
(11)
1.5 极限学习机(ELM)
极限学习机由Huang等[23]在2006年首次提出,在预测和综合评价领域显示了巨大的能力。ELM是一种新颖的快速学习算法,它随机地初始化输入权重和偏置,并获得单隐层神经网络的相应输出权重。
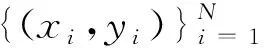
T=Hβ
(12)
(13)
在ELM中,H也被称为随机特征映射矩阵,wi=[wi1,wi2,…,win]T表示连接输入层神经元和隐藏层神经元i的输出权重,β=[β1,β2,…,βL]T表示输出层和隐藏层之间的权重矩阵,bi表示隐藏层神经元的偏置,T=[t1,t2,…,tN]T表示训练样本期望输出矩阵。隐藏层神经元的参数(wi,bi)根据任意连续抽样分布的概率随机产生后,给定训练样本,隐藏层输出矩阵H就是已知的和不变的,则式(12)就转化为求解线性系统T的最小参数最小二乘解了:
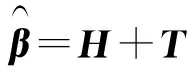
(14)
1.6 模型性能评估
为了验证所提出的模型的预测性能,计算了预测和观察的均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、相关系数(R2),见式(15)—(18):
(15)
(16)
(17)
(18)
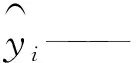
2 应用实例
2.1 白家包滑坡
白家包滑坡位于湖北省秭归县向家店村,长江支流湘西河右岸。距湘西河汇流处约2.5 km,距三峡大坝约30 km。滑坡俯瞰见图 1。滑坡头部位于280 m的高度,它纵向延伸550 m,横向延伸400 m,占地面积约22×104m2。自2003年6月三峡库区首次蓄水以来,滑坡前部的水位从海平面以上70 m上升到135 m,滑坡前部因此淹没在河流中。滑坡上部厚度约10~30 m,下部约20~40 m,平均斜角约为16°。
自2003年6月第一次蓄水以来,白家包滑坡运动较为明显,因此设立了多个以全站仪和测斜仪ZK-1为基础的应急地面监测点,对滑坡位移进行监测。随后2006年10月建立了预警监测系统,如图 2先后部署了4个GNSS(全球卫星导航系统)位移监测点,编号从ZG323到ZG326,对地表变形和滑坡位移进行监测。此外,2016—2017年还添加了3台新的GNSS监测设备,编号从Z00到Z02,以及3台裂缝测量仪,以加强整个系统的监测效果。同时安装了雨量计来收集降雨量数据。
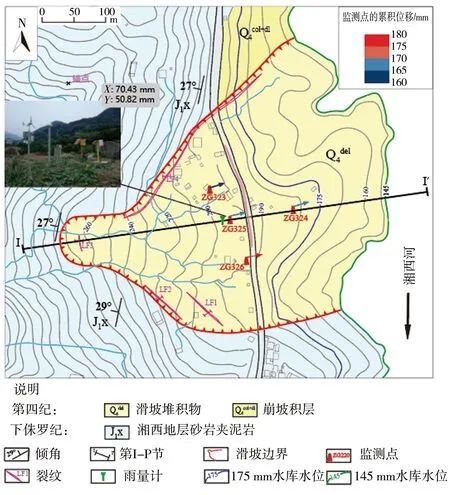
图2 白家包地理图以及预警系统
2.2 滑坡变形特征
自2003年6月22日,三峡库区第一次蓄水期间,白家包滑坡开始出现变形。主要表现为地面不连续裂缝,地面倾斜,见图 3。图 4是白家包滑坡的剖面,表明该滑坡处于向湘西方向整体运动的阶段,整体向西南倾斜约30°。图 5显示了GNSS监测的累积位移和位移数据。根据2003年以来收集的资料,白家包滑坡变形主要有5个阶段,见表 1。

图3 滑坡现场变形特性
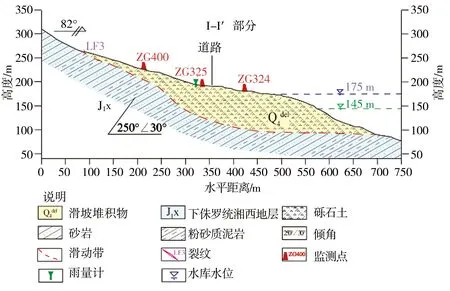
图4 白家包滑坡地区的地理剖面
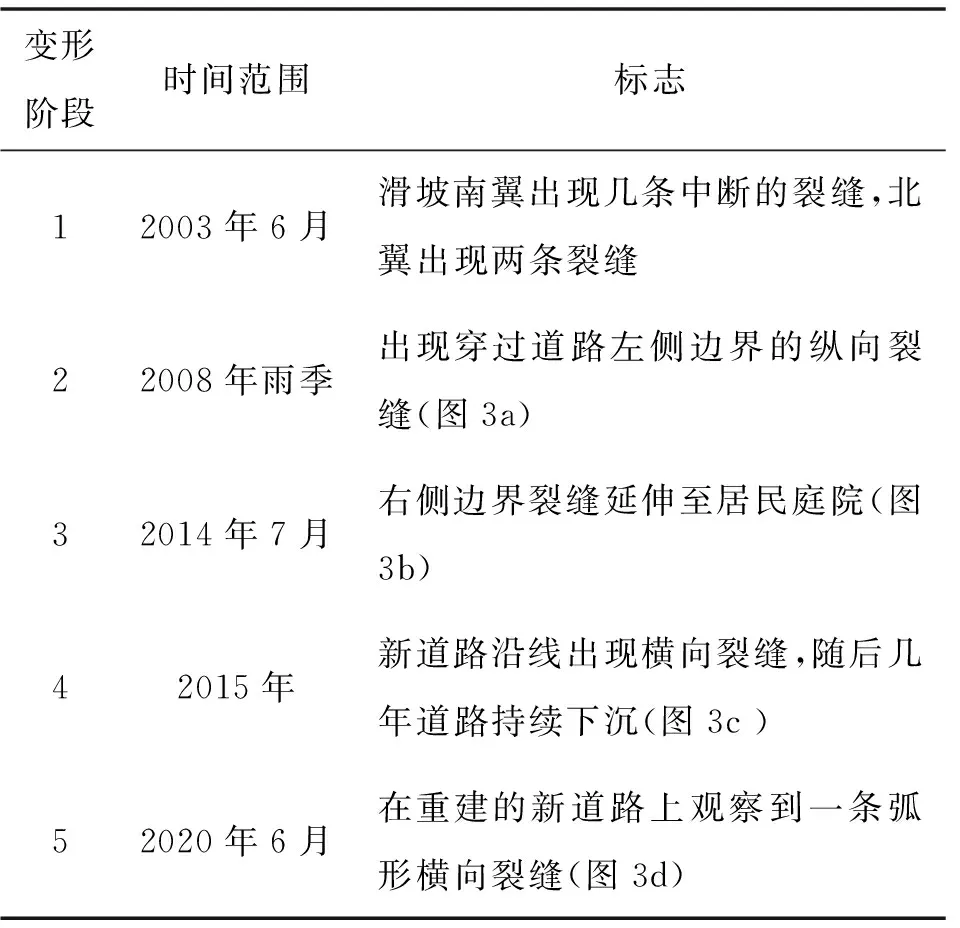
表1 滑坡变形主要标志
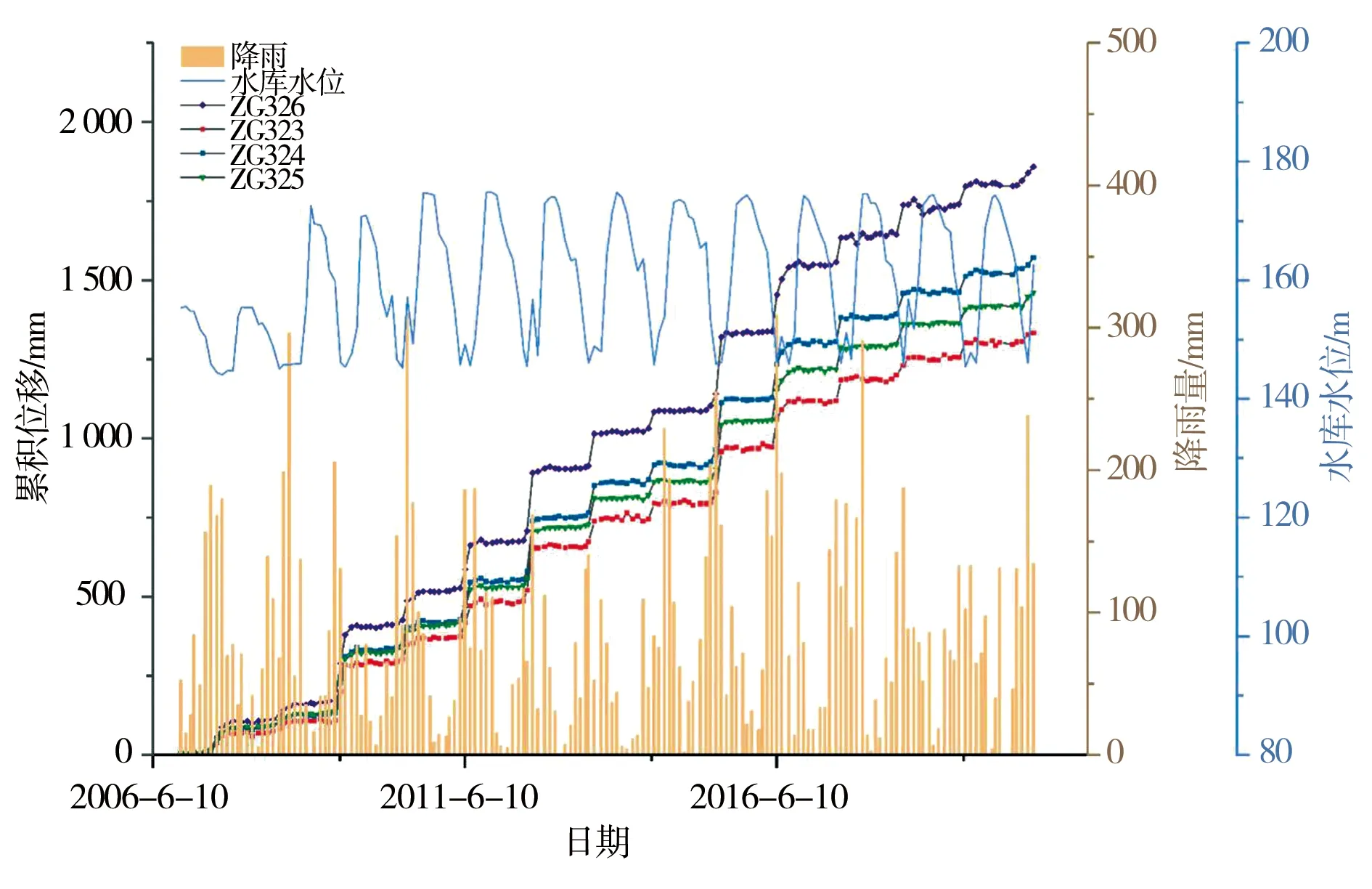
图5 白家包滑坡地区的监测数据
3 预测流程
图6给出了整体的方法框架。使用VMD将累积位移分解为2个模态(IMF),模态1构成滑坡的趋势项,模态2构成滑坡的周期项,然后,通过DES和PSO-ELM模型分别预测趋势项和周期项,最后,将预测得到的趋势项和周期项相加为总的预测位移。
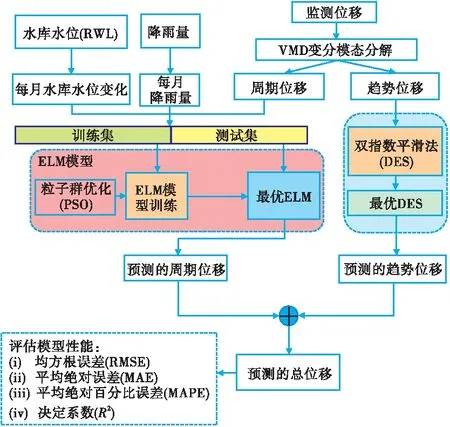
图6 位移预测流程
3.1 数据处理
使用ZG324的数据进行位移预测,在确定趋势位移时,使用了二次指数平滑法(DES),并使用回归系数R2检验。在确定周期位移时,考虑了影响因素,构建了PSO-ELM模型。在此使用灰色关联度(范围从0到1)评估了影响因素与周期位移之间的相关性,其中接近1的表示强相关性。在当前研究中,考虑大于0.7的值。同时,滑坡周期位移以及相关影响因素均已归一化。
利用2006年12月20日—2020年7月2日观测点观测到的数据作为研究对象,以月为单位对数据进行处理,共得到163月的数据,其中前115月数据作为模型的训练集,用于训练模型以及确定模型的相关参数;115—147月数据作为模型的测试集,用于比较各模型结果,确定最优预测模型;148—163月数据作为模型的验证集,比较最优模型预测的结果与实际位移之间的误差,验证该模型的可行性。
3.2 影响因子选择
影响因子的选择是提高位移预测准确性的关键。由于位移主要发生在雨季和水库水位波动的时期增加,降雨量和水库水位被认为是导致滑坡变形的主要影响因素[24-25]。此外,坡体的不同的状态也会对外界变化有不同的相应,当坡体处于稳定状态时,对外界变化响应较小,而处于临滑状态的坡体受外界变化影响较大,因此以前发生的位移也被认为是周期位移的影响因素[26]。对位移变化和库水位、降雨量等影响因素分量做灰色关联度分析后,选择本月降雨量、近两月降雨量、本月水库水位变化,近两月水库水位变化,近两月位移变化为影响因子。
3.3 归一化和逆归一化
对于机器学习算法,归一化可以使得数据处理更加方便,寻找最优参数更加容易,并提高模型的收敛速度和模型的精度。使用线性归一化,将每个原始数据转换到[0,1]的范围,见式(19):
(19)
式中X*——归一化后的值;X——原始值;Xmax——样本中最大的值;Xmin——样本中最小的值。
4 结果
本节通过案例说明了所提出方法的实施过程。此外,还采用了基于LSSVM、CNN-GRU等模型的预测方法,并与提出的方法进行了比较。
使用基于VMD将累积位移分解为了趋势位移和周期位移。趋势位移是近似单调增长的。趋势位移主要由代表滑坡长期固有行为和内部条件控制,如地质情况和结构。
图 7是用DES算法预测趋势位移的结果。图 8显示了趋势位移的测量值和预测值之间的回归关系,相关系数为0.999 73,表明了该方法的优良性能。
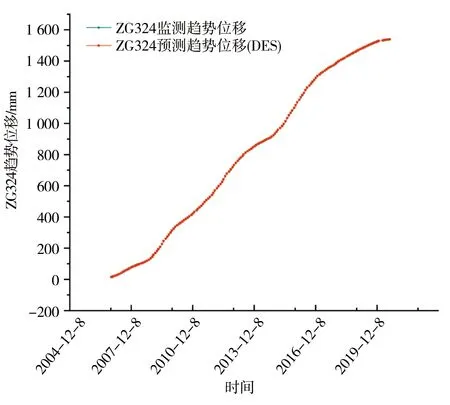
图7 监测趋势位移和预测周期位移
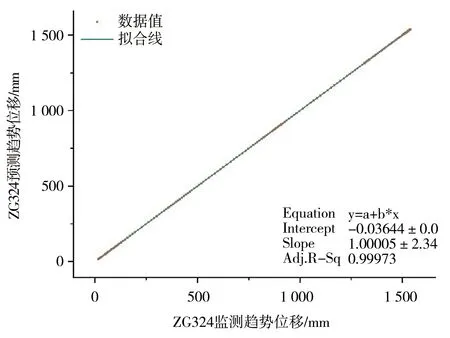
图8 趋势位移的拟合曲线
预测滑坡的周期性位移是一个关键问题。根据上述变形特征的分析,白家包滑坡的总位移受水库水位(RWL)和季节性降雨的控制。考虑到运动对地表状态演变和外部因素的依赖性,采用了6个主要影响因素,包括当月降雨量、上月水库水位变化、当月水库水位、上月水库水位、前两个月水库水位、上月周期性位移变化。这些主要因素被输入到PSO-ELM模型中,预测的结果见图 9。图 9表明,周期性位移的形状被准确捕捉,周期性位移的波峰和波谷被预测出来,这验证了输入主要影响因素的合理性和可靠性。图 10表明,测量值和预测值的相关系数为0.997 75(接近1表示精度高),这说明PSO-ELM是一种非常有效的周期性位移预测的方法。
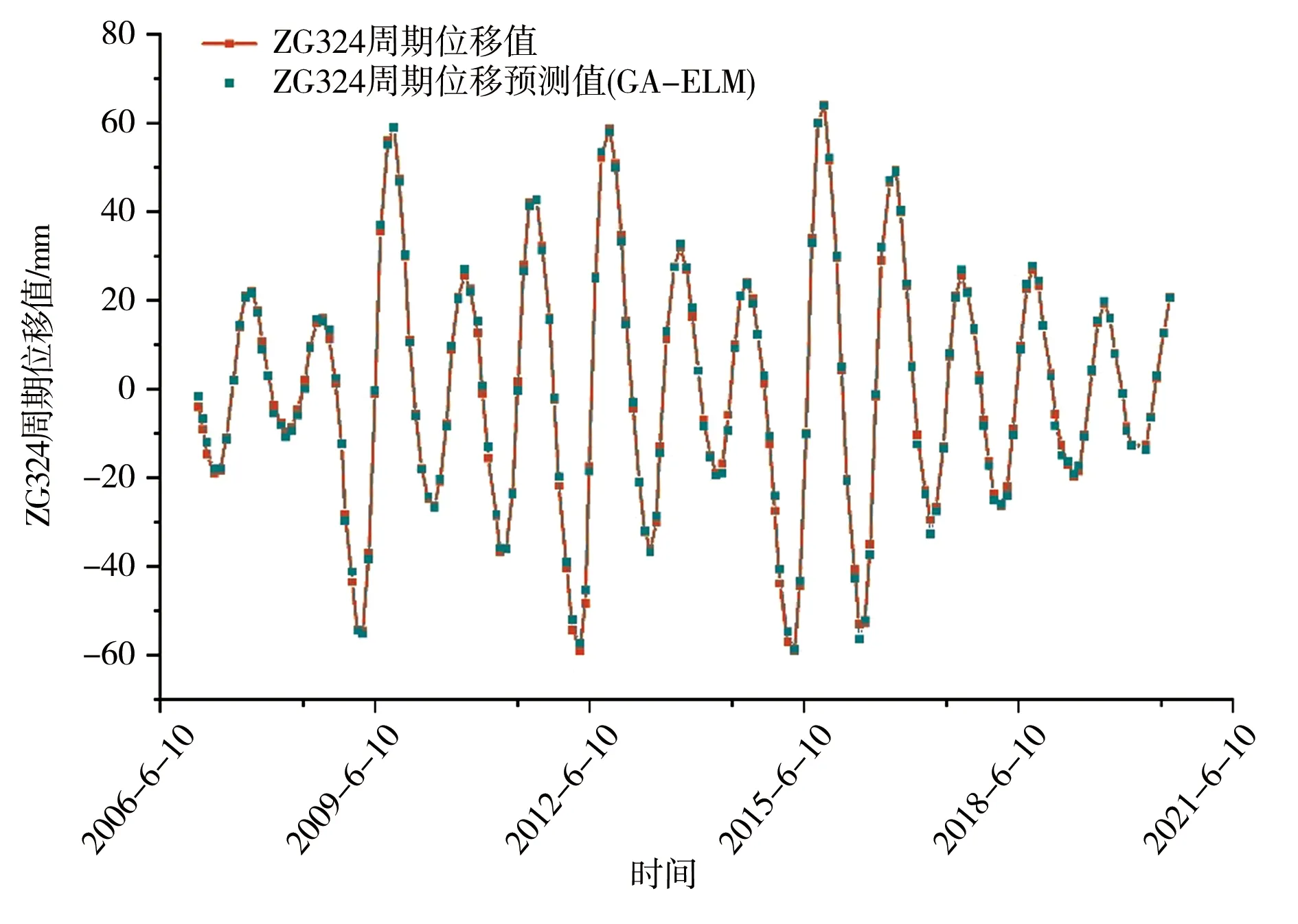
图9 监测周期位移和预测周期位移(PSO-ELM)
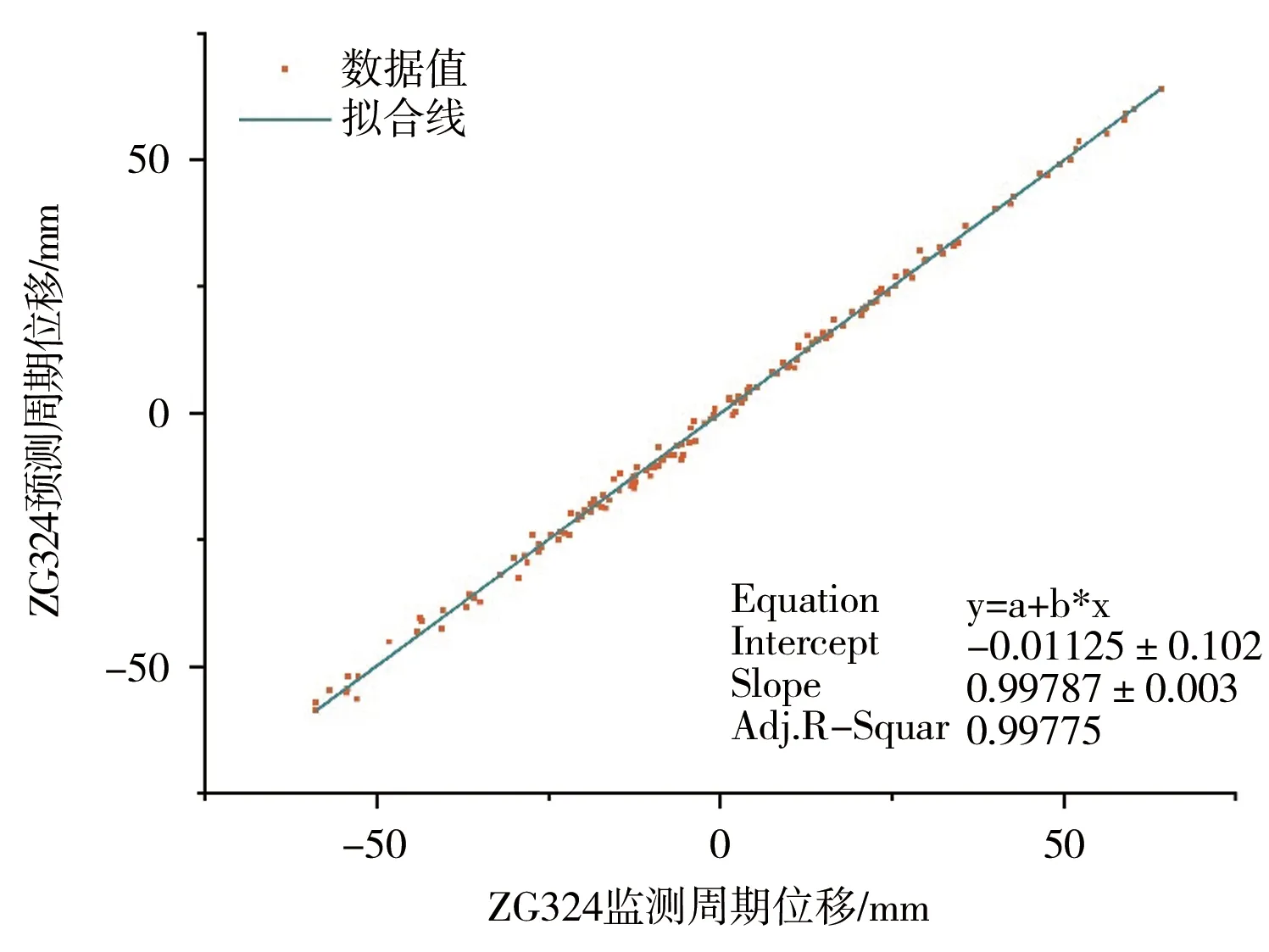
图10 周期位移拟合曲线
滑坡的总位移等于预测的趋势项和周期项之和。图 11显示,所提出的DES-PSO-ELM模型在预测实际检测位移上有出色的表现,在图 12显示相关系数为0.999 32,验证了所提出的机器学习模型的可实用性。
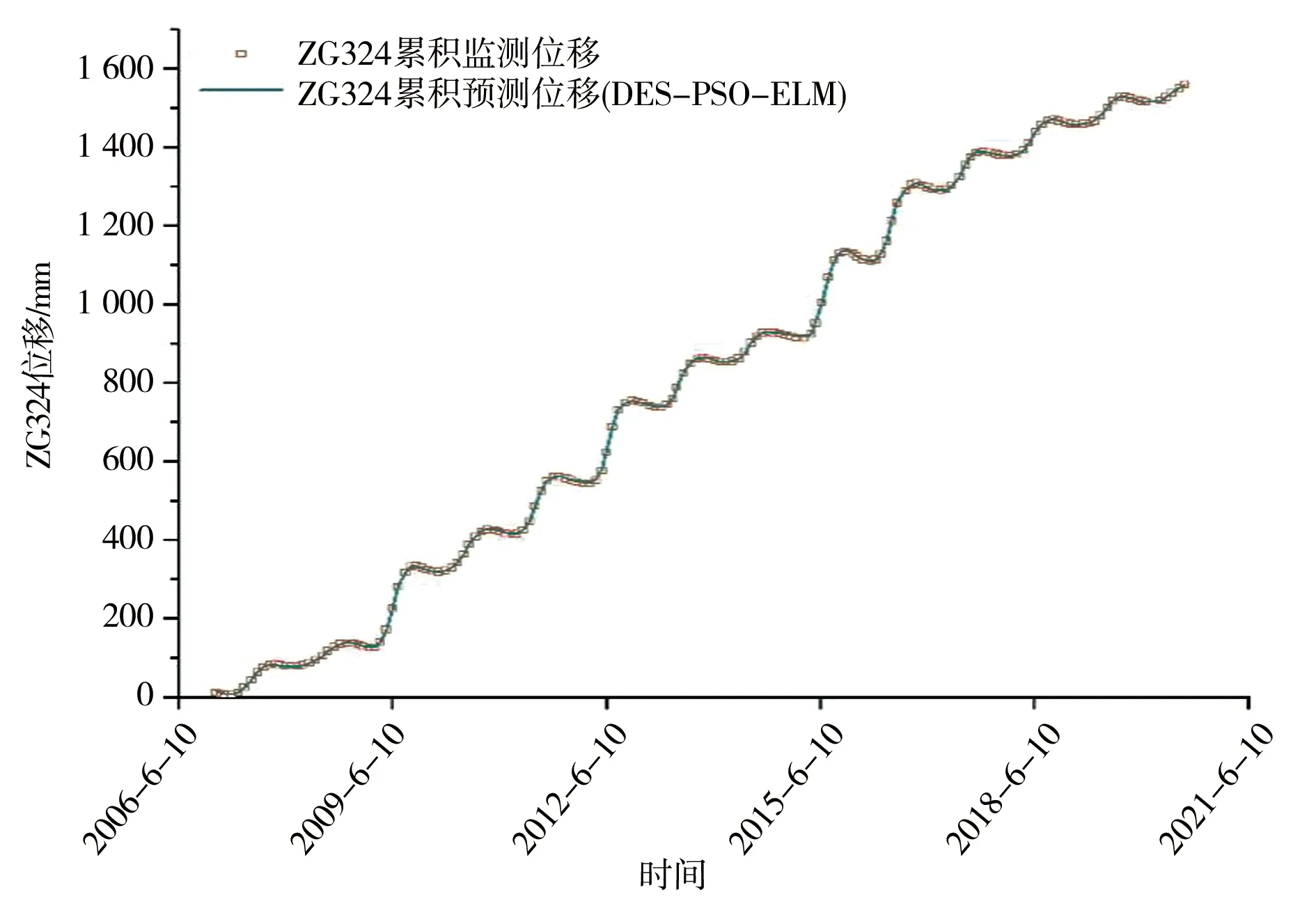
图11 监测总位移和预测总位移(PSO-ELM)
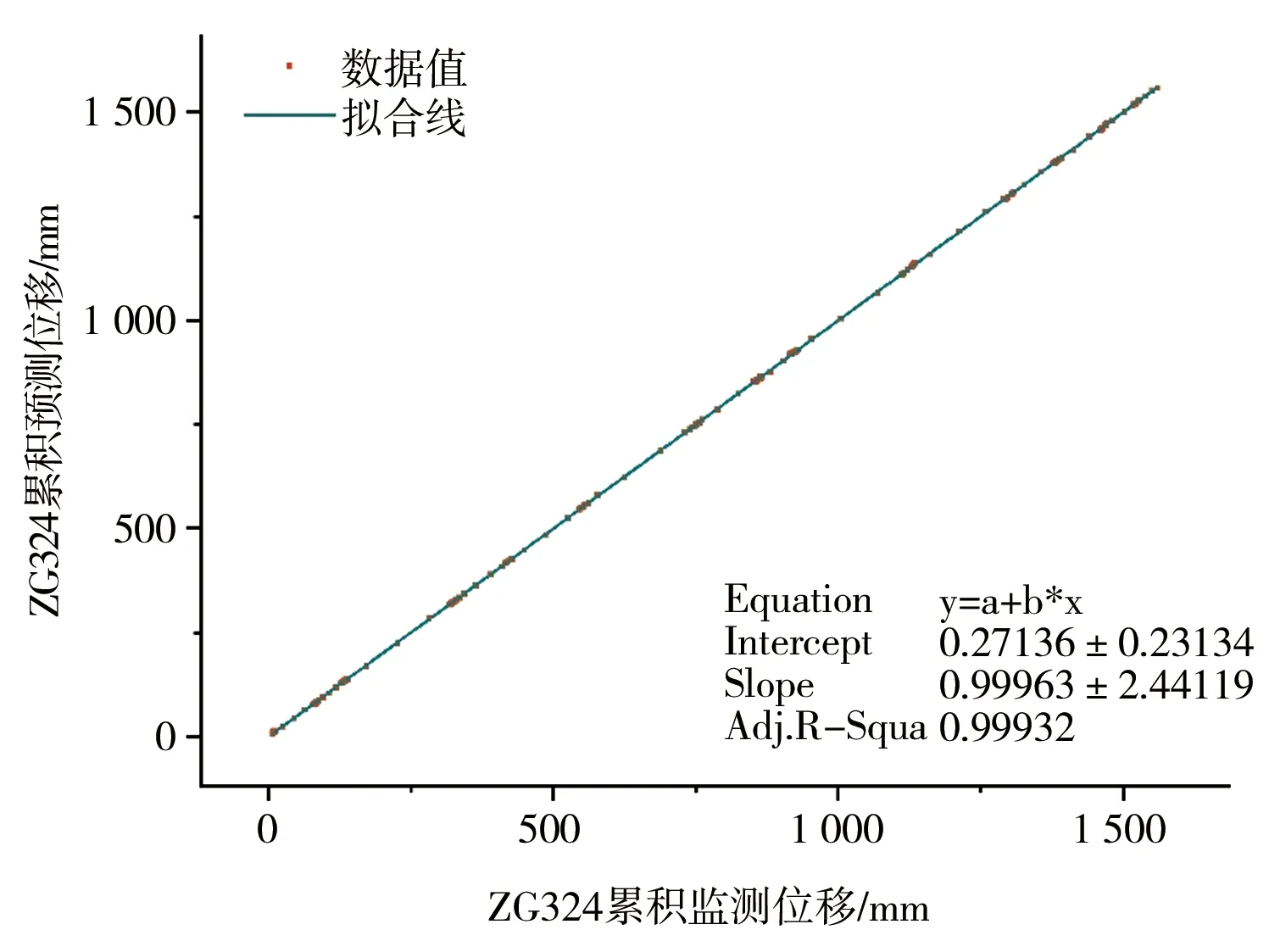
图12 总位移拟合曲线
此外,还使用了ELM模型、LSSVM模型CNN-GRU模型对滑坡的周期项位移进行了预测,以体现本模型的优越性。图 13显示了3种方法的预测结果,说明4种方法都能捕捉到周期性位移的变化规律,但LSSVM和CNN-GRU模型在波峰和波谷的变化较大。表 2列出了3种模型的预测结果。可以看出, PSO-ELM的RMSE、MAE、MAPE和R2是3个模型中最小的。总体而言,PSO-ELM在训练集、验证集和测试集上的表现都优于其他2个模型。
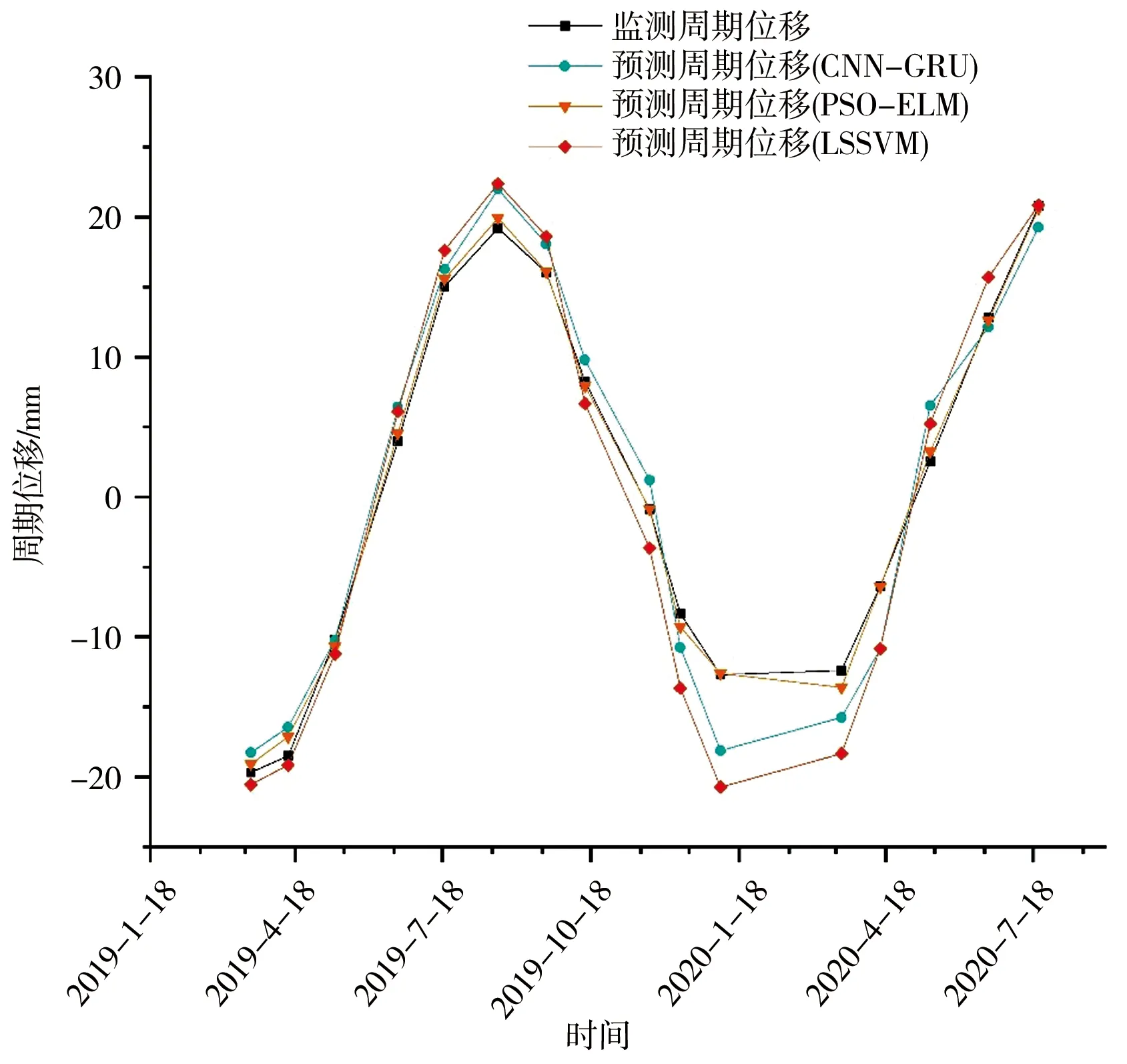
图13 不同模型的周期位移预测曲线
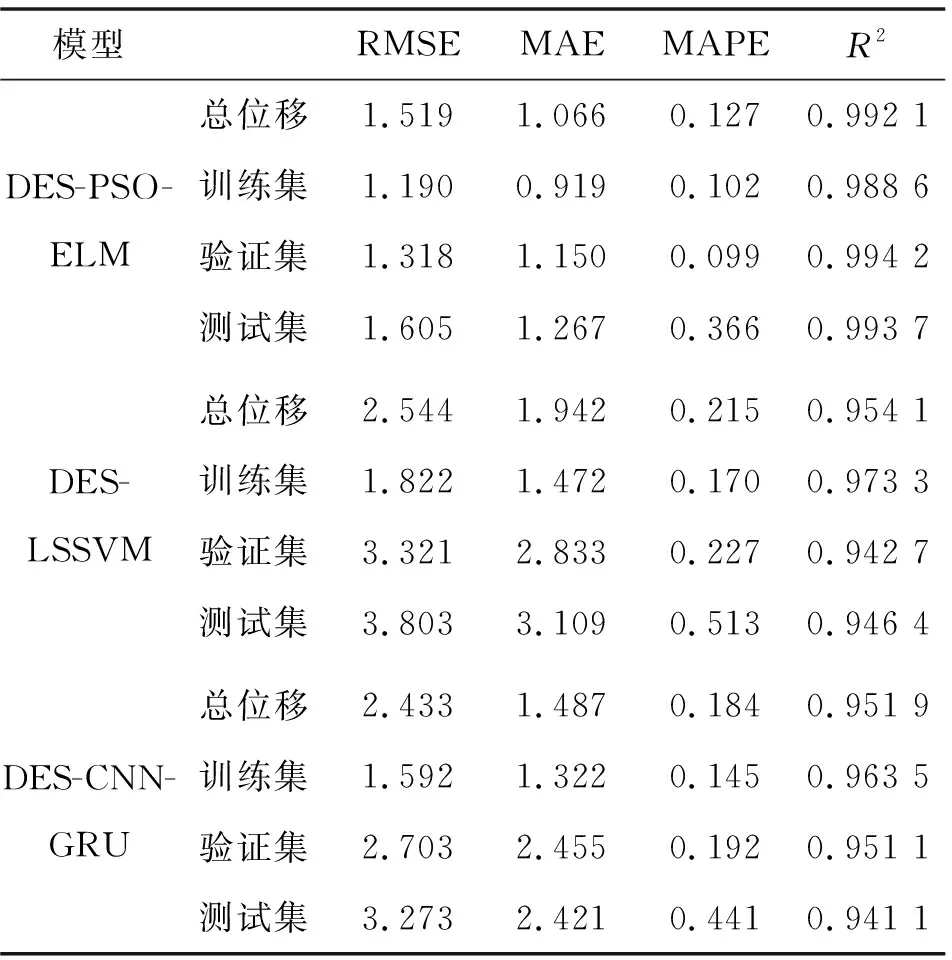
表2 不同模型的周期位移预测参数比较
5 结论
本文提出了基于滑坡多变量监测时间序列数据的位移预测模型,其预测结果对滑坡发展趋势研究和预警具有重要参考价值。以三峡库区白家包滑坡为例,基于滑坡位移与环境影响因素(降雨量和水库水位)的相关性,建立了DES-PSO-ELM混合集成模型,并利用广泛用于时间序列数据处理的DES-LSSVM和DES-CNN-GRU模型进行比较。在大多数情况下,DES-PSO-ELM模型在预测上优于其余模型。[2-4]
a)在ZG324上,DES-PSO-ELM模型在测试集上的RMSE、MAE、MAPE和R2分别为1.287、0.993 mm;0.008、0.999 32,DES-PSO-ELM模型在预测滑坡位移的准确性明显优于其他模型。由于PSO优化算法是优化当前数据集,对于其他监测点的效果不是很理想,需要对其他监测点的数据集进行重新训练。
b)在2.2节中,可以看到在每年的雨季,滑坡的位移急剧增加。虽然模型在本研究中取得了较好的结果,但是在降雨量或水库水位剧烈变化的情况下,位移的预测误差不可避免的会增加。因此,解决这类问题是非常重要的研究方向。本研究考虑的影响因素主要是降雨量、水库水位和滑坡本身的位移,找到其他影响因子也是未来应该考虑的方向。
c)滑坡预测的结果可以应用于滑坡敏感性绘图以及滑坡风险分析,因此本文提出的模型也可以尝试应用于滑坡预警中。
