基于VMD-LSTM-ARMA模型的径流预测

罗灿坤,刘 昊,黄 鑫,邵 壮

(国网湖南综合能源服务有限公司,湖南 长沙 410001)

河川径流作为重要的水文要素之一,由于受到降水、气温和人类活动等诸多各种因素的影响,显示出复杂、随机、多维等特征[1]。人类活动以及全球气候变暖等各种因素导致了水资源时空分布失衡态势,从而增加了非线性、非平稳性径流预测难度[2]。同时,径流预报不准确也会为梯级水电站优化调度带来困难[2-3]。准确的径流预测对于解决旱涝灾害,梯级水电站优化调度,保证水利设施正常运行及提升其经济效益都具有重要意义[4]。因此,国内外水文工作者致力于研究径流特点,找寻预测结果更加精确的方法。目前,比较常见的径流预测方法有很多,例如数理统计法、物理成因法等[5-6]。随着计算科学技术的迅速发展以及关于径流预报方法的深入研究,许多基于现代智能方法和数值天气预报的综合预报模型逐渐被提出,主要包括模糊分析[7]、灰色系统理论[8]、混沌理论[9]、小波分析理论[10]、人工神经网络[11]等,这些方法的应用可以有效地提高径流预测结果的可靠性和精度。

目前,国内外的径流预测大都偏向于通过建立新的预测模型来提高精度。但是,基于径流时间序列的复杂性分析,单一的模型难以充分反映径流形成的复杂性和影响因素的多样性,导致对于整个径流序列的拟合性较差,预测可靠性不高。由此,综合采用多种预测方法的径流预报方式近年来受到水文研究者的广泛关注。综合近年来水文工作者的研究成果分析,一般的混合模型多是采用各种分解方法对径流数据进行处理,而后代入预测模型进行径流预测。从数据结果分析,预测精度和稳定性得到了较好的提升。近年来,对于径流数据的时频分析因其良好的效果而被研究者逐渐运用于水文分析之中[12-13]。基于时频分析,将原始径流序列分解,处理结果为多个不同频率的子序列,通过这样的方式可以使得径流序列趋于平稳化,而后将各子序列分别代入模型,这样的方式对提高预测的精度效果显著[14]。张敬平等[15]提出了经验模态分解与径向基函数神经网络混合径流预测模型,模型预测结果具有较高的精度;Giulia等[16]建立EMD-ANN(Empirical Mode Decomposition-Artificial Neural Network)分解-集成模型,较好地减少了径流预测误差;刘艳等[17]通过玛纳斯河的局部信息运用集合经验模态分解(EEMD,Ensemble Empirical Mode Decomposition)预处理,而后代入整合移动平均自回归(ARIMA,Auto Regressive Integrated Moving Average Model)模型,验证了模型预测的准确性;赵力学等[18]运用变分模态分解(VMD,Variational Mode Decomposition)和BP神经网络(Back Propagation Neural Network)组合模型来水位流量的非线性预测,取得较好的结果。上述研究表明,基于时频分析的分解技术对于提升径流预测精度效果明显。但是,现有的处理方法大多是对径流序列进行处理后,采用相同预测模型对子序列进行预测,没能很好地考虑子序列的差别性和独特性。

因此,提出了一种新的组合预测方法,基于不同时序分析方法,采用VMD方法对径流数据进行分解,利用LSTM方法对于长时间序列具有较好的泛化性和ARMA模型对于平稳序列具有良好的预测效果等特点对不同频率的模态进行预测,通过VMD对径流数据的处理结果分析,所得低频的模态很好地继承原始数据的时间特性,选用LSTM神经网络进行处理,而高频的模态通过了平稳性检验,采用ARMA模型进行预测,最后将不同模态的预测结果叠加,得到径流预测数据。

1 算法原理

1.1 利用VMD算法将径流数据分解

VMD算法作为一种新的信号处理方法,是在经验模态分解(EMD,Empirical Mode Decomposition)的基础上改进所得。作为一种新的非递归、自适应、准正交信号分解方法,VMD算法通过参数预设,将时间序列数据分解为指定个数的固有模态分量(IMF,Intrinsic Mode Function)。VMD算法将数据从时域转化到频域进行分解,不仅可以很好地捕捉时间序列数据的非线性特征,还能避免变量信息重叠,其分解过程具有很强的鲁棒性。

VMD算法将径流数据的分解问题转化为变分问题,见式(1):

(1)

式中f(t)——径流数据;δ(t)——冲激函数;{u}={u1(t),u2(t),…,uk(t)}——分解后得到的K个模态分量;{ω}={ω1,ω2,…,ωK}——各模态分量所对应的中心频率;*——卷积运算符。

然后,引入二次惩罚因子ɑ和拉格朗日算子λ(t),用于求解上述变分问题,得到扩展的拉格朗日表达式,见式(2);并采用交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)迭代搜索,迭代后的uk、ωk以及λ见式(3):

L=({uk},{ωk},λ)=

(2)

(3)

式中ω——频率;γ——噪声容忍度。

(4)

此时,径流数据被分解为K个不同频率的时间子序列。

1.2 利用LSTM预测径流数据的低频子序列

作为特殊的循环神经网络(Recurrent Neural Network,RNN),LSTM(图1)与传统的时间序列算法相比,可以避免长依赖问题,可以解决时间序列中较长时间间隔和延迟的时间序列问题。

图1 LSTM神经元内部结构

其具体计算方法见式(5):

ft=σ(Wf·[ht-1,xt]+bf)

(5)

式中ft——t时刻的遗忘门;σ——sigmoid 函数;bf——遗忘门的偏置项;Wf——权重矩阵;[ht-1,xt]+bf——2个向量拼接为1个新的向量。

当前的输入xt保存到单元状态Ct的量由输入门决定,见式(6)、(7):

it=σ(Wi·[ht-1,xt]+bi)

(6)

(7)

当前时刻的单元状态Ct的计算见式(8):

(8)

输出门的计算见式(9)、(10):

σt=σ(W0·[ht-1,xt]+bo)

(9)

ht=Ot·tanh(Ct)

(10)

式中Ot——输出;tanh——激活函数。

本文所搭建的网络中,时间窗口步长设置为1 d,不仅调用了LSTM神经网络用来处理低频子序列,还设置了多个用全连接层搭建的隐藏层和relu激活函数,用来提取特征解决非线性问题,因此更加适合处理时间序列数据。

1.3 ARMA模型

ARMA模型是基于线性自回归模型(Autoregressive Model,AR)和滑动平均模型(Moving Average Model,MA)建立起的平稳时间序列处理模型。ARMA模型可以描述为:

yn=φ1yn-1+φ2yn-2+…+φpyn-p+εn-θ1εn-1-…-θqεn-q

(11)

式中yn——径流数据的预测值;{yn-1+yn-2+…+yn-p}——前p个时刻的径流数;{εn,n=0,1,2,…}——白噪声序列;{φ1,…,φp}——AR模型的系数;{θ1,…,θp}——MA模型的系数,要确定p和q的取值,需要进行多次尝试与检验。

1.4 VMD-LSTM-ARMA模型构建

利用VMD对径流进行分解,可以得到若干个复杂度低的子模态。对所得模态进行ADF单位根检验,用以区别平稳与非平稳模态。以往基于时序分解的组合模型未考虑分解子序列的差异性,因此,本文考量了分解模态的特征,选取LSTM与ARMA模型,将非平稳及平稳子模态分别代入进行预测,最后将所得结果叠加即得到原始序列预测结果。组合模型建模流程见图2。

图2 模型流程

2 模型评价

为衡量预测模型的精准度和可靠性,本文选取了较为常用的2种评价指标:平均绝对误差(Mean Absolute Error ,MAE )和均方根误差(Root Mean Square Error ,RMSE)。

(12)

(13)

3 算例分析

耒水属于长江流域的湘江水系,干流全长439 km,流域面积11 905 km2。东江水文站设立在资兴市东江镇耒水左岸,是国家重要基本水文站,控制集水面积4 659 km2,站类为一类精度站。

采用东江水文站2020年实测径流数据,样本的采样周期为1 h,选取日期为2020年1月1日至2020年12月31日。原始径流数据见图3(为了更好地展示数据趋势,只取前240个点)。

图3 前10 d数据展示

从图中分析,该径流数据具有比较强的非平稳性和非线性,采用一种时间序列预测模型(如LSTM、ARMA模型)难以保证预测结果的精度及可靠性。综合考虑原始数据特点,本文利用VMD算法对于信号在频域剖分的优势进行原始径流序列的处理。需要注意的是,模态数(K)的取值会影响VMD分解的效果:当K的取值较小,径流数据中的一些重要信息会丢失,从而影响后续的预测精度;当K的取值较大时,邻近的模态分量的中心频率距离变小,会导致模态重叠或产生噪声。因此,K的取值可以通过观察来确定,即对相邻模态分量进行相关性分析或者观察不同模态下的中心频率的分布情况。

此外,为了确定分解后的模态是否是平稳序列,可以对模态分量进行单位根(ADF)检验,即确定时间序列中的单位根是否存在。若不存在单位根,则数据为平稳的时间序列;若存在单位根,则数据为非平稳的。VMD参数设置见表1。参数α、τ和ε的设置参考了文献[19],K的选择主要依据分解后各模态的频率分布情况以及预测结果(例如若K=4,可以发现模态3、4的频率分布几乎没有差别,而且预测效果比K=3时的预测结果差)。

表1 VMD算法参数设置

利用VMD算法将径流数据分解出3个IMF,分别命名为IMF1、IMF2、IMF3。然后分别对3个模态进行平稳性检验。原假设:检验的时间序列具有单位根,函数的返回值为检验统计量、p值和临界值在1%、5%、10%置信区间。IMF1的p值为0.09,大于显著性水平(α=0.05),因此可以认为IMF1中的时间序列没有通过ADF检验,是非平稳的时间序列;然后对于IMF2、IMF3进行平稳性检验,p值同为0.001,小于显著性水平(α=0.05),时间序列没有单位根(特征根在单位圆之内),因此可以认为IMF2和IMF3中的时间序列通过了ADF检验,是平稳的时间序列。

此外,分解后的3个模态中,IMF1频率较低,继承了原始径流数据的变化趋势,基本上剔除了随机干扰噪声的影响,具有明显的时间序列特征,因此可以采用LSTM神经网络预测;而IMF2和IMF3数据幅值较小,频率较大,呈现出一种类似于高斯白噪声的数据类型,属于平稳的时间序列,可以利用ARMA模型预测,见图4—6。因此,需要采用不同的预测算法对数据进行处理,然后再对每个分量预测结果进行重构,则可以得到更加准确的预测效果。

图4 VMD分解出的第一个分量

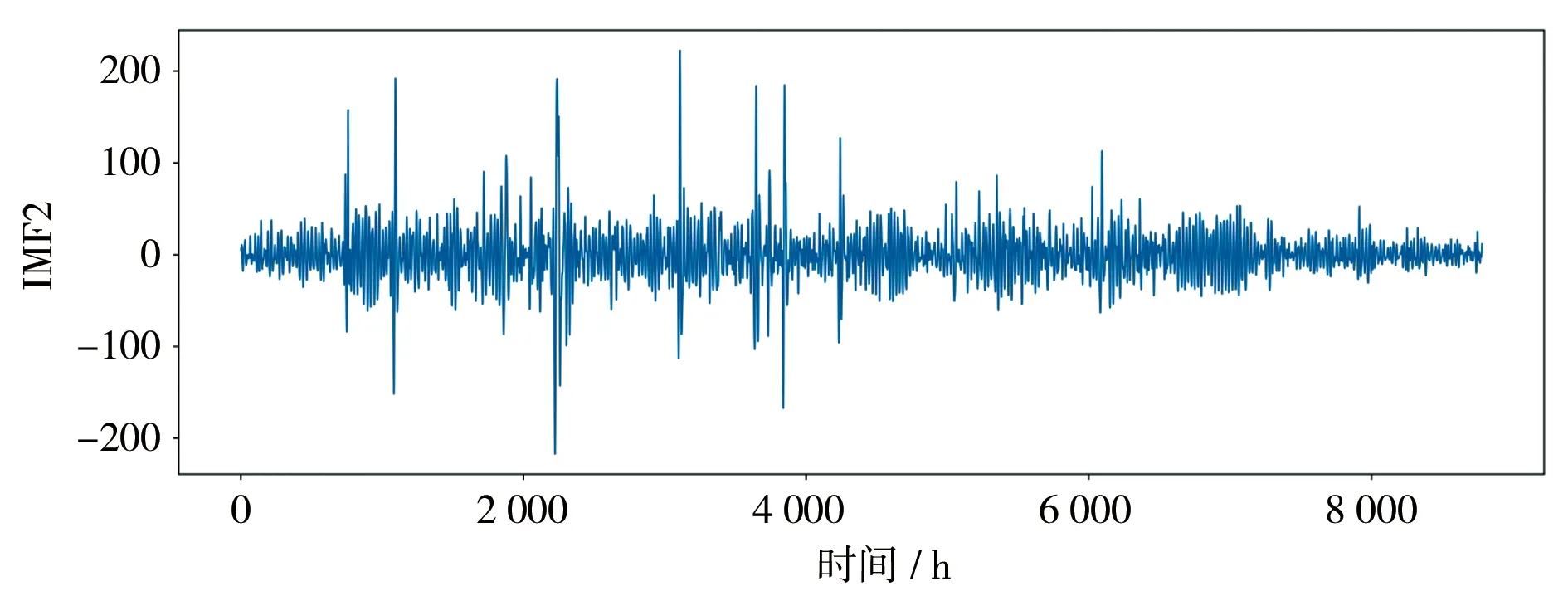
图5 VMD分解出的第二个分量

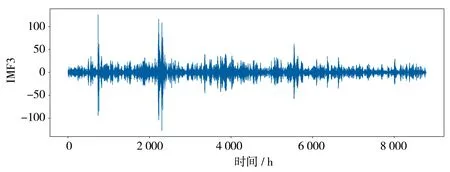
图6 VMD分解出的第三个分量

3.1 采用LSTM神经网络预测IMF1

为了更好体现径流受历史径流的影响,本文采用预测日前5天的数据作为训练样本。其次,为了满足水电站制定调度计划的需求,对预测日当的数据进行预测,即将前5天的数据作为特征,后1天的数据作为标签。将IMF1划分训练集和标签,生成的训练样本为8 784×120 的矩阵,生成的标签样本为8 784×24 的矩阵。按照7∶3的比例划分训练集和测试集,即训练集的特征样本为6 149×120的矩阵,标签样本6 149×24的矩阵;测试集的特征样本为2 635×120的矩阵,标签样本为2 635×24的矩阵。系统环境为Windows10-64位系统,Python版本3.8.5,IDE为PyCharm,利用 TensorFlow的前端 Keras搭建 LSTM 神经网络进行时间序列分析。LSTM模型参数:隐藏节点24,激活函数为relu,迭代次数为50。在建立LSTM神经网络结构后,为了防止过拟合,在全连接层后面加入Dropout层,从而提高泛化能力。优化器选用Adam,损失函数选用mae。当训练集和测试集的训练误差逐渐减少且趋于稳定时,可以认为LSTM神经网络拟合完毕。

利用LSTM算法对IMF1进行预测,损失函数随迭代次数的变化情况见图7。可以看出,随着迭代次数的增加,准确率逐渐升高,损失函数逐渐减小。

图7 LSTM损失函数随迭代次数变化曲线

3.2 采用ARMA模型预测IMF2和IMF3

ARMA模型的输入数据为IMF2和IMF3的前3×24个点的值预测接下来24个点的值。经过多次尝试和检验,本案例的ARMA模型的参数为:p=1,q=0。

3.3 预测结果对比分析

为了得到径流数据的预测结果,将IMF1、IMF2与IMF3各自的预测结果进行叠加。为了验证本模型对径流数据预测的可靠性和精准度,本文引入另外几种常见的径流预测模型进行比对,包括LSTM神经网络、ARMA模型、随机森林(Random Forest,RF)和支持向量机(Support Vector Machine,SVM),采用MAE和RMSE进行定量分析,见表2、图8。

表2 预测评价指标对比 单位:m3/s

a)实际-组合模型

由表2可知,与其他4种算法的预测结果相比,本文提出的VMD-LSTM-ARMA组合模型的MAE与RMSE最小,径流预测结果更为精准。此外,为了直观体现模型预测效果及差异,本文将原始径流数据(取其中400个点)与VMD-LSTM-ARMA组合模型及其他4种对比模型预测值可视化,结果见图8,4种对比模型的预测值与原始数据的拟合度较低,与本文提出的组合模型相差较大,说明VMD-LSTM-ARMA模型具有较高的预测精度,是一个有效的模型。

4 结语

从径流时间序列的非线性、复杂性特征角度考虑,采用时频分析方法,基于VMD分解,充分考虑径流数据分解所得模态的特点,考量LSTM对非平稳低频模态和ARMA模型对平稳高频模态的优势,建立起了VMD-LSTM-ARMA模型,以东江水文站逐小时流量数据为例进行预测,并与LSTM、BP、随机森林和SVM等常见单一模型进行结果比对,性能分析,得出如下结论:①采用VMD分解方法可以有效提取径流时间序列中不同频率的固有信息,通过分解,较好地降低了原始数据的非平稳性,降低了预测难度;②针对分解所得模态的差异性,分别选取LSTM与ARMA模型进行预测,对于提升预测精度效果明显,通过与比对模型比较,与直接将原始径流序列代入模型预测相比,基于分解的组合模型预测效果更理想;③本文提出的组合模型将VMD、LSTM与ARMA模型的优点有机结合起来,在预测时间序列的表现要优于单一模型,具有较高的精度和可靠性。