聚焦立体几何中的动态问题

■童昌立

立体几何的动态问题的实质是数学建模问题,解这类问题,需要有较强的空间想象能力和化归处理能力。对于动态立体几何问题,如果能努力探寻运动过程中“静”的一面,动中求静,往往能以静制动。

题型1：截面问题

例1如图1,用一个平面去截直三棱柱ABCA1B1C1,分别交A1C1,B1C1,BC,AC于点E,F,G,H。若A1A＞A1C1,则截面的形状可以为____。(把你认为可能的结果的序号填在横线上)

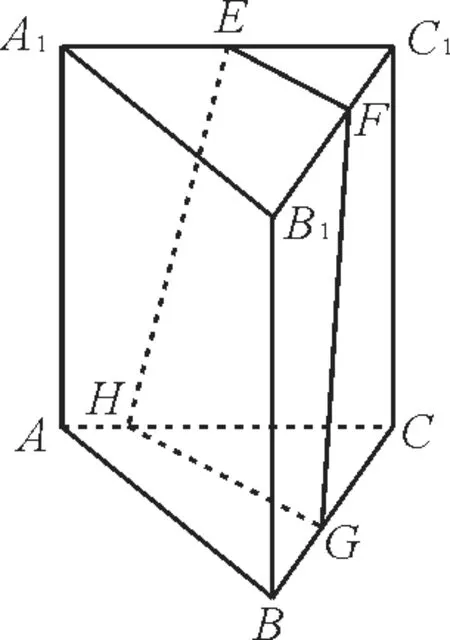
图1

①一般的平行四边形,②矩形,③菱形,④正方形,⑤梯形。

解析

由ABC-A1B1C1为直三棱柱,可知平面A1B1C1//平面ABC。因为截面过平面A1B1C1、平面ABC,所以交线EF//HG。当FG不与B1B平行时,此时截得的EH不平行于FG,则四边形EFGH为梯形;当FG//B1B时,此时截得的EH//FG,且FG⊥EF,则四边形EFGH为矩形。答案为②⑤。

点评

熟记平面图形的性质是解题的关键。

题型2：角度问题

例2设异面直线a,b所成的角为30°,经过空间一点O有且只有两条直线与异面直线a,b成等角θ,则θ的取值范围为_____。

解析

如图2,过O作a1//a,b1//b,则a1,b1所成的角,即为异面直线a,b所成的角。

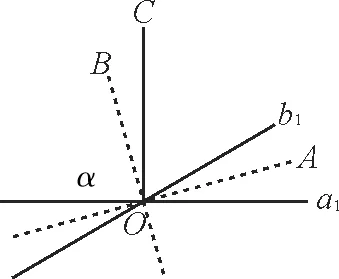
图2

记a1,b1确定一个平面为α,过O作OC⊥α,过O作直线OA和直线OB分别平分a1,b1形成的两个对顶角。

当过O的直线在平面AOC内旋转时,与a1,b1所成的角为θ,且15°≤θ≤90°;当过O的直线在平面BOC内旋转时,与a1,b1所成的角为θ,且75°≤θ≤90°。

结合对称性可知,若经过空间一点O有且只有两条直线与异面直线a,b成等角θ,则θ的取值范围为15°＜θ＜75°。

点评

两条异面直线所成角的范围是0°＜θ≤90°。

题型3：平行问题

例3如图3所示,在正四棱柱ABCDA1B1C1D1中,E,F,G,H分别是棱CC1,C1D1,D1D,DC的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则点M只需满足条件_____时,就有MN//平面B1BDD1。(请填上你认为正确的一个条件即可,不必考虑全部可能情况)

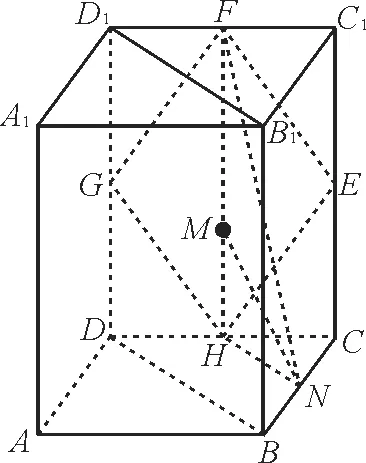
图3

解析

由题意得FH//DD1,HN//BD,FH∩HN=H,DD1∩BD=D,所以平面FHN//平面B1BDD1。只需M∈FH,则MN⊂平面FHN,这时MN//平面B1BDD1。

故满足条件的点M在线段FH上(或点M与点H重合)。

点评

本题属于开放性问题,解题的关键是证明MN//平面B1BDD1。

题型4：垂直问题

例4如图4所示,在棱长为1的正方体ABCD-A1B1C1D1中,点E是 棱BC的 中点,点F是棱CD上的动点。试确定点F的位置,使得D1E⊥平面AB1F。

解析

当点F为CD的中点时,D1E⊥平面AB1F。

因为A1B⊥AB1,A1D1⊥AB1,又A1D1∩A1B=A1,所以AB1⊥平面A1BCD1。因为D1E⊂平面A1BCD1,所以AB1⊥D1E。

因为DD1⊥平 面ABCD,所 以DD1⊥AF。又AF⊥DE,所以AF⊥平面D1DE,所以AF⊥D1E。又AF∩AB1=A,所以D1E⊥平面AB1F。故当点F是CD的中点时,D1E⊥平面AB1F。

点评

本题主要考查线面垂直的判定与性质。探求满足条件的点的问题,一般可考虑特殊情况,如线段的中点,三等分点等。

题型5：轨迹问题

例5如图5,已知线段AB垂直于定圆O所在的平面,B,C是☉O上的两个点,H是点B在AC上的射影,当点C运动时,点H运动的轨迹是( )。

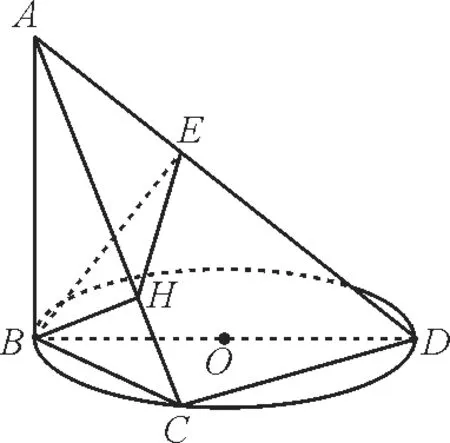
图5

A.圆 B.直线 C.线段 D.三角形

解析

过点B作☉O的直径BD,连接CD,AD,则BC⊥CD。

过点B作BE⊥AD于点E,连接EH。因为AB⊥平面BCD,所以AB⊥CD。因为BC⊥CD,且AB∩BC=B,所以CD⊥平面ABC,所以CD⊥BH。

又BH⊥AC,且AC∩CD=C,所以BH⊥平面ACD,所以BH⊥AD,BH⊥HE。

注意到过点B与直线AD垂直的直线都在同一平面内,于是结合点B,E的位置,可知当点C运动时,点H的运动轨迹是以BE为直径的圆。应选A。

点评

立体几何中的轨迹问题,涉及的知识点较多,需要熟记直线、圆、球等几何图形的性质。

感悟与提高

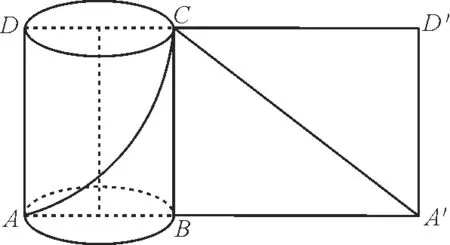
图6