基于改进扩展卡尔曼滤波的AUV单信标定位研究

陈允锋,陶健龙

(1.海军装备部驻上海地区第九军事代表室,上海 20206;2.上海交通大学,上海 200240)

0 引 言

近年来,自主水下航行器(AUV)作为海洋开发中应用最广泛的自动化装备,能够代替人类在环境恶劣、危险系数高的深海中完成多样化水下作业任务,如海洋资源勘测、水下捕捞和目标跟踪等[1],已经成为人类认识海洋、了解海洋不可或缺的装备之一。而获取准确的位置信息是AUV完成预定任务的必要条件,适用于陆地、水面和空中的北斗、GPS等定位系统,主要借助电磁波信号进行定位。但电磁波信号在海水高导电介质中传播会快速衰减,该类方法应用于水下环境时无法提供可靠的定位信息。因此,AUV的精准定位具有挑战性。

主流的AUV导航定位方式包括惯性导航、地球物理导航和声学导航[2]。惯性导航无需发送任何信号,常用于隐蔽性要求高的AUV,但长航程由于累积误差,定位偏移可达数十米。地球物理导航根据携带的声学或光学传感器重建周边地理信息,是一种能够实现全球水下自主导航的方式。声学导航利用声波在水下良好的传输特性以及信标、应答器等设备实现高精度的定位。

单信标导航作为声学导航的一种方式,于1995年被Scherbatyuk首次提出[3]。相比于其他声学导航方式,具有经济性高、易于布置等优势,在水下导航中拥有很大的应用潜力。Yu等[4]提出基于变分贝叶斯近似的鲁棒自适应单信标导航方法,克服现有单信标导航方法在伴随有效声速误差、测量异常值和未知噪声统计参数时定位精度差的问题。Zhu等[5]针对现有单信标定位模型通常为二维状态,引入水深状态量,建立新型三维单信标定位模型。Liu等[6]引入时钟平衡因子,缓解时钟不同步对于水下滑翔机单信标定位的影响。Ssac等[7]针对几何构型不当引起单信标异步导航精度低问题,提出一种基于相位差的水下机器人导航方法。Koshaev[8]提出基于多模型的AUV单信标导航算法,采用1组扩展卡尔曼滤波算法,无需AUV的初始状态信息。Zhao等[9]为抑制标准扩展卡尔曼滤波线性化带来的误差,将融合自适应网络和模糊推理系统改进的扩展卡尔曼滤波算法用于单信标定位。

为提高AUV单信标导航的定位精度,本文在标准扩展卡尔曼滤波算法基础上,融合多新息和遗忘因子,提出基于改进扩展卡尔曼滤波算法的AUV单信标导航定位方法。充分利用不同时刻的新息,降低线性误差带来的不确定性,但过多地使用历史数据会造成误差累积。因此,在状态更新时引入遗忘因子区分新旧数据,削弱数据饱和。最后通过仿真实验验证本文提出方法的有效性和准确性。

1 单信标定位状态空间描述建立

1.1 运动学方程

AUV航行过程中的深度信息可以通过深度传感器准确获得,因此,能够将三维定位问题简化为二维问题。为便于研究,以单信标所在位置为惯性坐标系原点,建立二维平面坐标系,如图 1所示。AUV位置表示为(ξ,η),其相对周围流体的运动速度表示为v,艏向角表示为ψ。

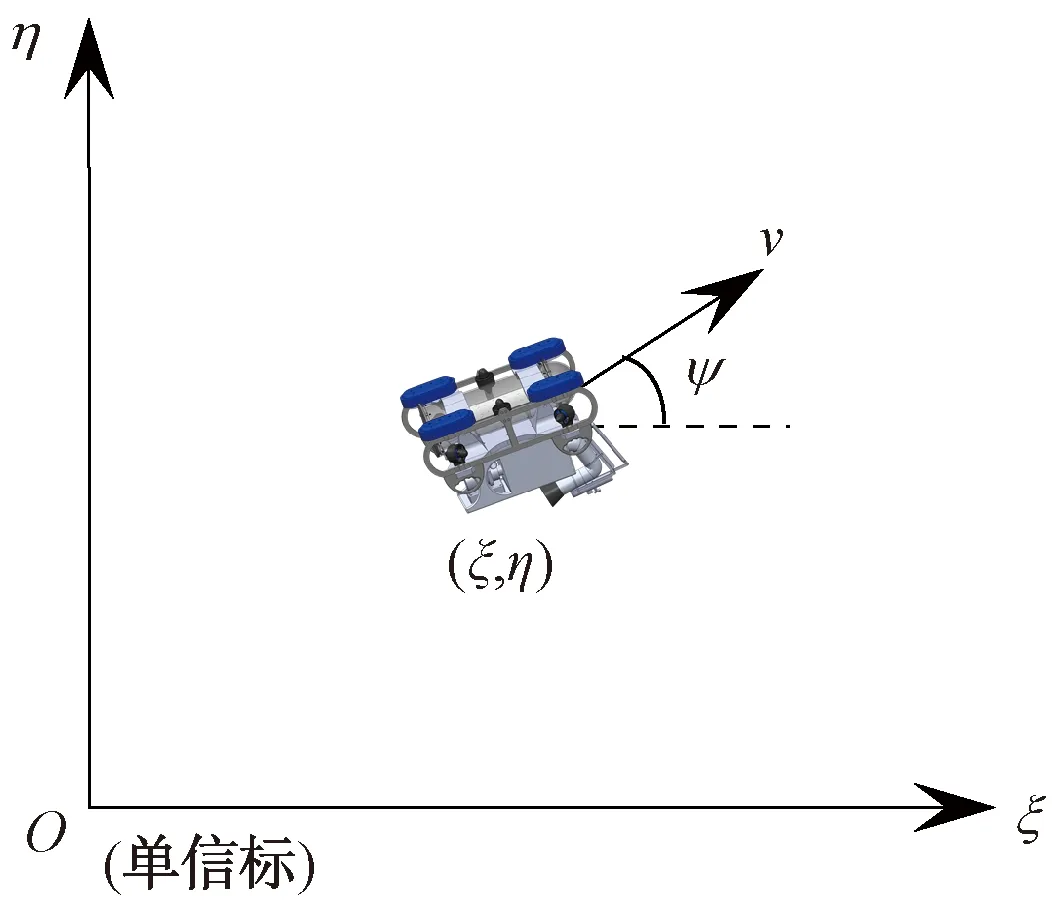
图1 AUV位置坐标系

以AUV在东向、北向的位移分量ξ(t)、η(t)和水流速度在东向、北向分量vE、vN为状态变量,系统在控制输入u=(v,ψ)作用下AUV单信标导航系统的运动学方程可表示为:

(1)

将式(1)使用如下状态空间描述,标准形式为:

(2)

式中:vξ(t)=v(t)cosψ(t),vη(t)=v(t)sinψ(t),分别代表AUV速度在东向和北向的分量。

定义采样时间间隔Δt=t-t0,假设采样间隔内u(τ)=u,单信标定位状态空间描述离散化后为:

Xk=AXk-1+Buk-1+Wk-1

(3)

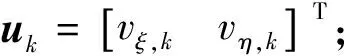
(4)

(5)

1.2 观测方程

观测量包括AUV与信标之间的水平距离和水流速度,第k时刻的水平距离可表示为:

(6)

通过多普勒测速仪测得AUV对地速度va与计程仪测得相对速度v之差,可表示为:

(7)

为符合真实环境,加入均值为0的传感器测量噪声Vk,其符合高斯噪声分布,即Vk～(0,Rk),Rk为测量噪声的协方差矩阵。结合式(6)和式(7)得到观测方程为:

Zk=h(Xk)+Vk

(8)

(9)

2 改进扩展卡尔曼滤波算法

2.1 标准扩展卡尔曼滤波算法

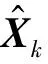
(10)

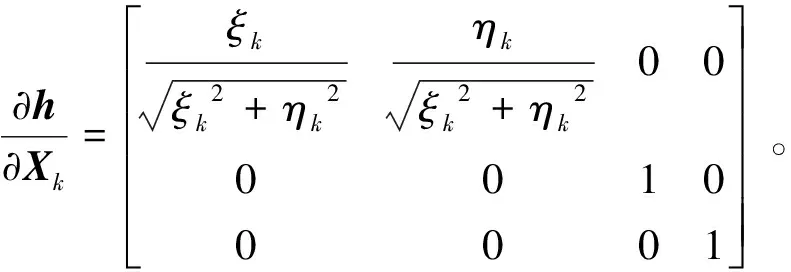
Xk=AXk-1+Buk-1+Wk-1

(11)

(12)

基于标准扩展卡尔曼滤波的AUV单信标导航定位算法迭代流程如下:

(1)参数初始化

(2)时间更新

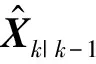
(13)

(14)

(3)新息更新

(15)

(16)

(4)滤波增益矩阵更新

(17)

(5)状态更新

计算当前时刻滤波输出:

(18)

(6)协方差阵更新

Pk|k=(I-KkCk)Pk|k-1

(19)

(7)令k=k+1,再次执行(2)。

2.2 融合多新息理论和遗忘因子改进算法

新息是指能够提升状态估计精度的有效信息[10]。从标准扩展卡尔曼滤波算法估计AUV 第k时刻状态时的迭代流程可知,仅使用前一时刻的标量新息,隐藏在历史数据中的有效信息无法充分利用,当系统非线性较强时,可能导致滤波器无法收敛。为充分利用当前时刻及历史量测数据,降低线性化误差,增强AUV定位精度,将单新息标量拓展为多新息向量形式,表示为:

(20)

式中:p表示新息长度,p≥1,使用滑动窗口的方式进行数据更新,将新息长度作为窗口大小。

为保证矩阵计算时维数相容,将卡尔曼增益矩阵扩展为如下形式:

(21)

但考虑到当前时刻的数据在AUV定位中利于精度提升,而过多引入历史数据可能会产生误差累积,导致数据饱和现象。因此,在多新息的基础上加入遗忘因子,削弱历史数据中误差累积的影响。改进后的状态更新方程可表示为:

(22)

(23)

式中:Γ(p,k)=ΛK(p,k),Λ=diag{λ1,λ2,…,λp},为遗忘因子矩阵,其中元素λi为数据权重;α代表遗忘因子。

基于改进扩展卡尔曼滤波的AUV单信标定位算法递推流程如图 2所示。相比于标准扩展卡尔曼滤波算法,不仅在时间维度上增加了相邻时刻数据使用量,而且考虑了新旧数据的重要程度,减小了误差累积作用,提高了扩展卡尔曼滤波算法在单信标导航定位中的准确性和稳定性。

3 仿真分析

为验证融合遗忘因子的多新息扩展卡尔曼滤波(改进MIEKF)在AUV单信标定位应用中的有效性和准确性,本文借助MATLAB软件设计了仿真实验,对比算法包括标准扩展卡尔曼滤波(EKF)和多新息扩展卡尔曼滤波(MIEKF)。航迹起始点为(-500 m,500 m),在600～1 000 s,1 100～1 300 s时AUV前进航速为4 m/s,其余时刻航速为2 m/s,东向、南向水流速度分别为0.3 m/s、0.4 m/s,采样间隔时间为1 s。采用AUV估计位置与真实位置之间的欧氏距离作为定位误差,表示为:

(24)

(1)无先验位置偏差下的定位准确性分析

探究改进MIEKF在正确初始状态时的定位准确性,与EKF和MIEKF算法进行仿真对比分析。AUV初始位置为(-500 m,500 m),不同算法的定位结果如图 3和表 1所示。

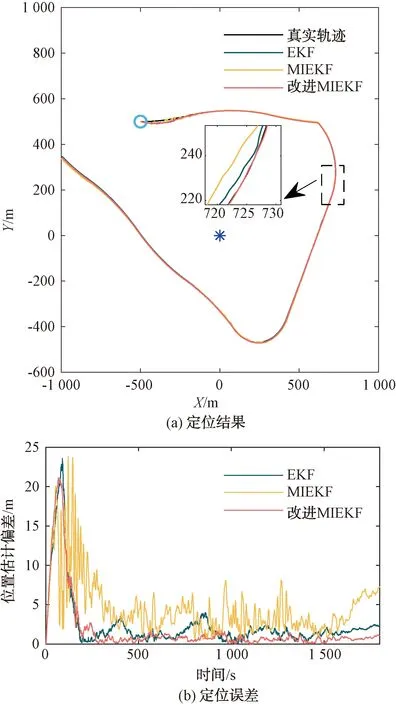
图3 不同算法定位准确性对比

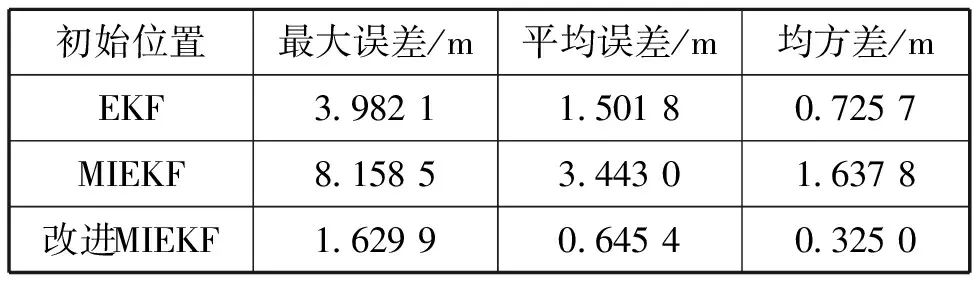
表1 不同算法定位误差统计

图3中“*”表示单信标位置,可以看出3种算法均能准确地获得AUV实时位置信息。改进MIEKF算法收敛时间稍逊于EKF算法,MIEKF算法误差累积逐渐增大,预测位置和实际位置之间存在较大偏差。在调整阶段,EKF算法的最大定位偏差为23.5 m,改进MIEKF算法最大定位偏差为21 m,收敛时间稍逊于EKF算法。由于融合了遗忘因子和历史数据进行修改,改进MIEKF算法整体定位精度和稳定性优于标准卡尔曼滤波算法,最大定位误差减少2.352 2 m,定位误差平均值减少0.856 4 m,验证了改进算法良好的定位能力。

(2)先验位置偏差对改进算法性能的影响

AUV实际工作时很难获得准确的先验位置信息。因此,进一步探究改进MIEKF算法在不同先验位置偏差下的收敛性与准确性。设计3种不同先验位置进行分析,AUV实际初始位置分别为(505 m,505 m)、(510 m,510 m)和(515 m,515 m),新息长度p= 5,遗忘因子α= 0.3。不同先验位置偏差仿真结果如图 4和表 2所示。

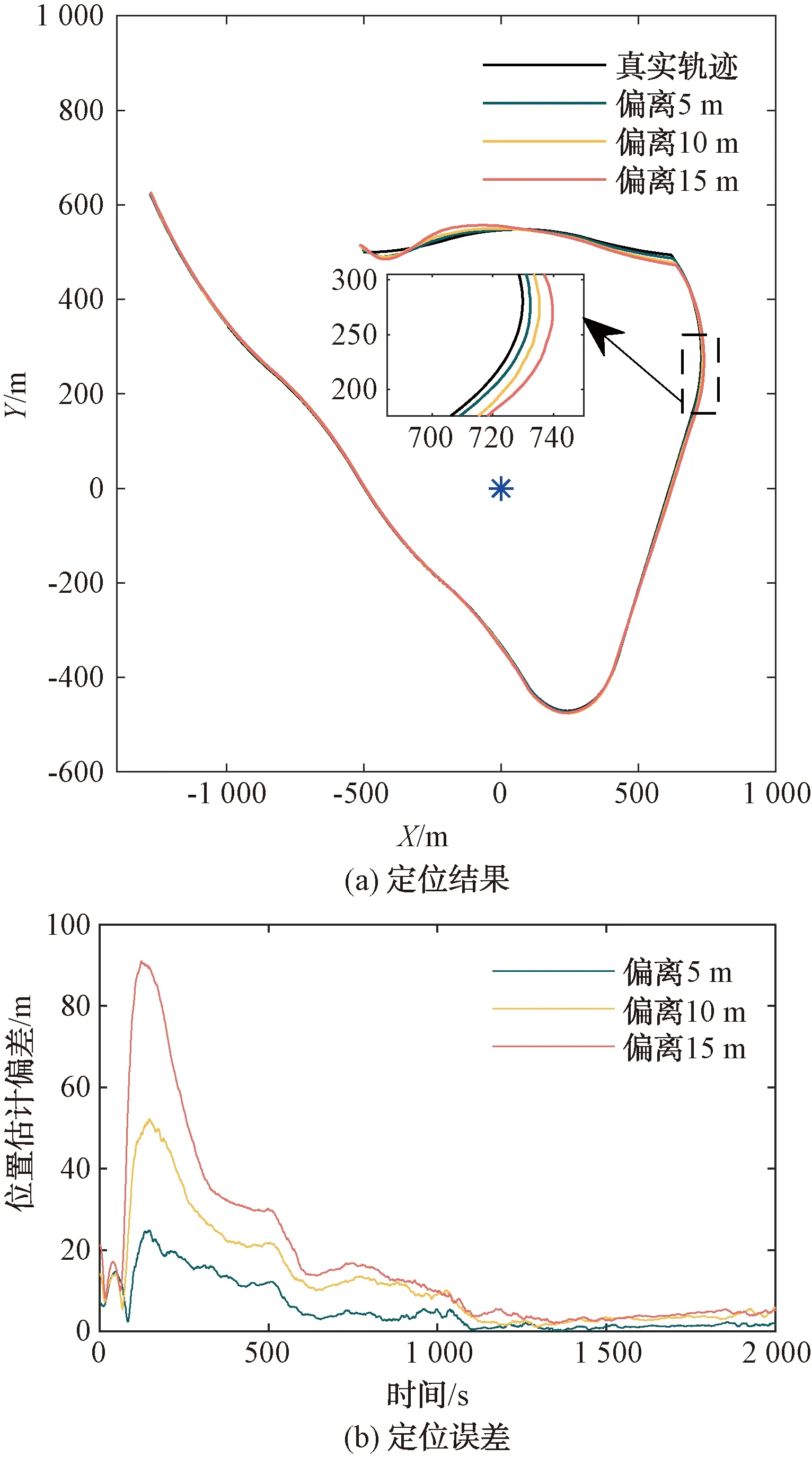
图4 不同先验位置偏差定位准确性对比

从图4和表2中可以看出,本文的改进算法均能在1 100 s内收敛到预定航迹附近。仿真结果中,最大定位误差在米量级,平均定位误差优于4 m,并且滤波器收敛精度与初始状态偏差相关,初始状态与实际值越接近,定位精度越高。

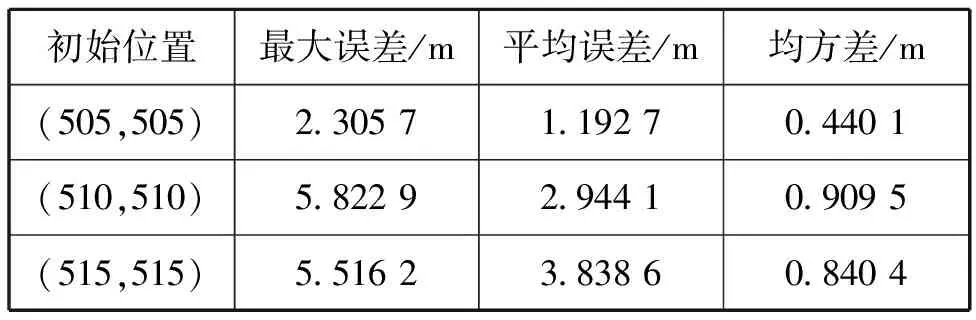
表2 不同先验位置偏差定位误差统计

(3)新息长度对改进算法性能的影响

历史数据使用量与新息长度相关,对改进算法定位精度有较大的影响。采用控制变量法,AUV实际初始位置为(500 m,500 m),遗忘因子α= 0.3,新息长度p依次设置为2、4、6、8和10,同时与EKF算法进行对比。定位结果如图 5、图 6和表 3所示。收敛时间随新息长度增加而增加,最大收敛时间约为400 s。收敛精度和稳定性随新息长度增加而增加,但当新息长度超过6时,其收敛精度趋于某一固定值。相比于以单新息修正的EKF算法,改进算法平均定位误差比标准EKF算法至少降低25%。在该工况下,新息长度选取6～8时定位算法性能达到最佳。

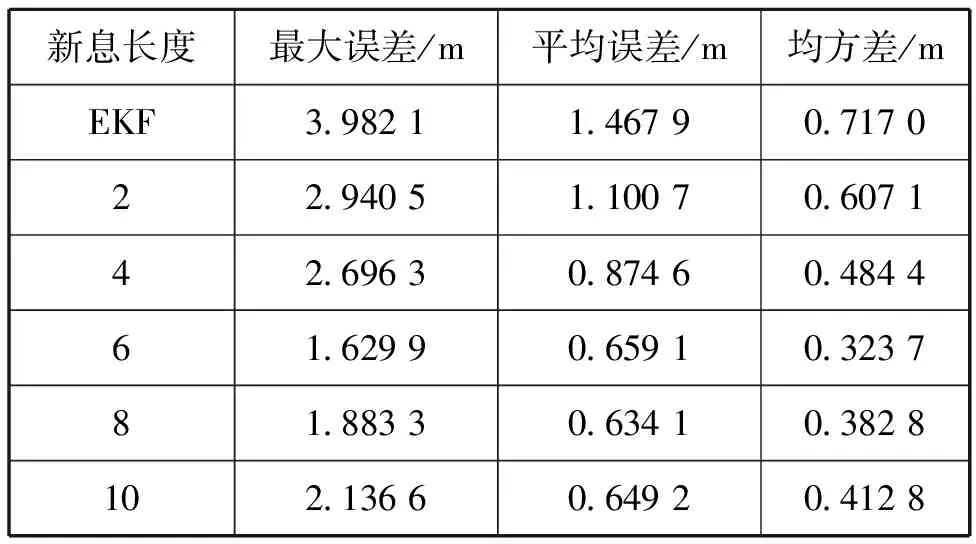
表3 不同新息长度定位误差统计

图5 不同新息长度定位结果对比

图6 不同新息长度定位误差

(4)遗忘因子大小对改进算法性能的影响滑动窗口内新、旧历史数据权重与遗忘因子大小相关。由遗忘因子定义形式可知,当遗忘因子设置过小,遗失了(k-p+1,k-2)时刻数据中有利的信息,多新息作用减弱;设置过大,则会使k-1时刻数据权重变小,修正项中无法充分利用前一时刻数据,AUV定位误差增大。采用控制变量法,AUV实际初始位置为(500 m,500 m),新息长度p= 6,选取遗忘因子分别为α=0.1、0.3、0.5、0.7。定位结果如图 7、图 8和表 4所示,当遗忘因子为0.3时,位置估计最大误差、平均误差、均方差分别为1.629 9 m、0.659 1 m和0.323 7 m。当遗忘因子为0.7时,各项误差显著增加,接近遗忘因子为0.3时的2倍,且稳定后波动范围较大,算法性能降低。综上可知,改进算法的平均定位误差随遗忘因子增加呈先降低后增加的趋势。

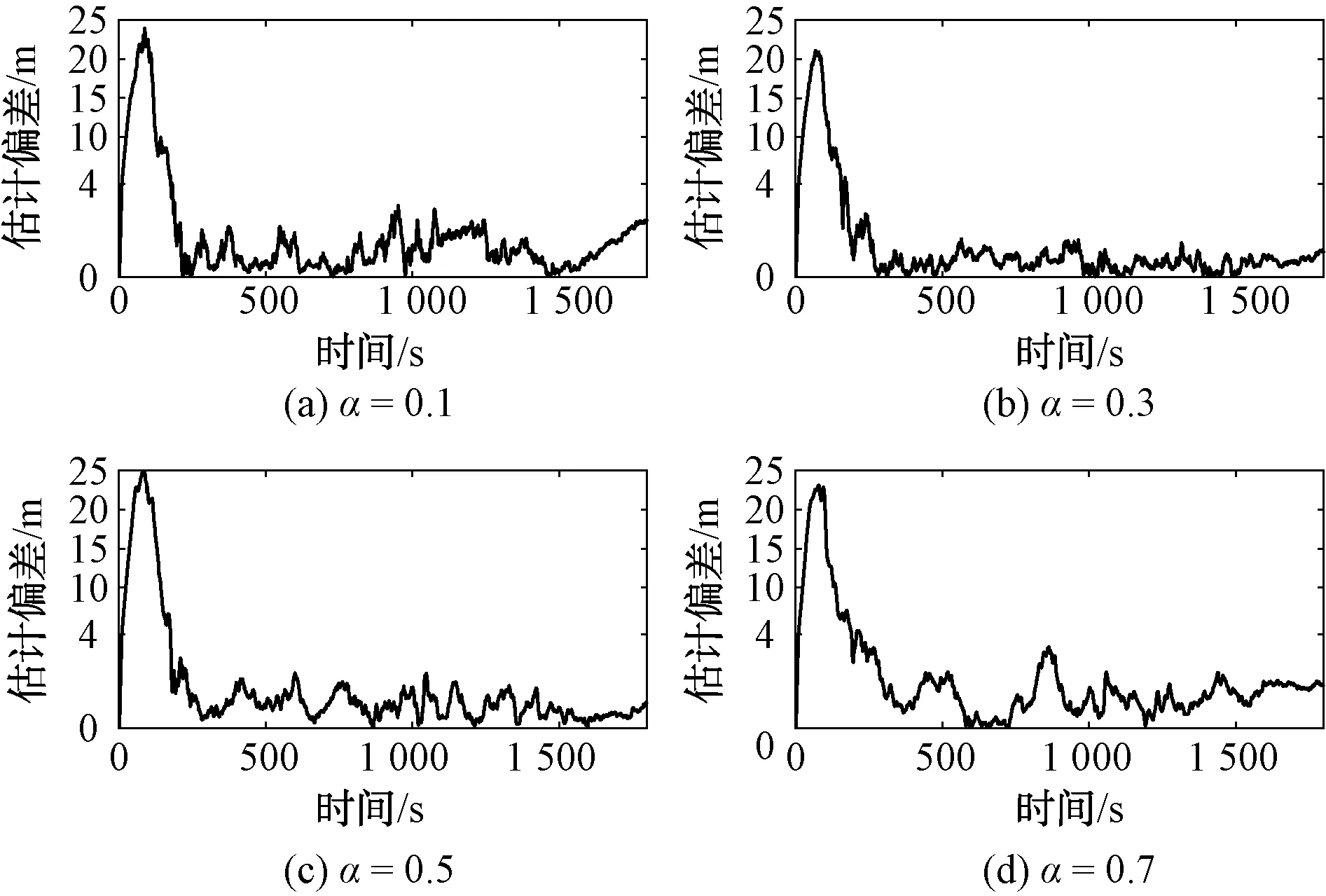
图8 不同遗忘因子定位误差对比

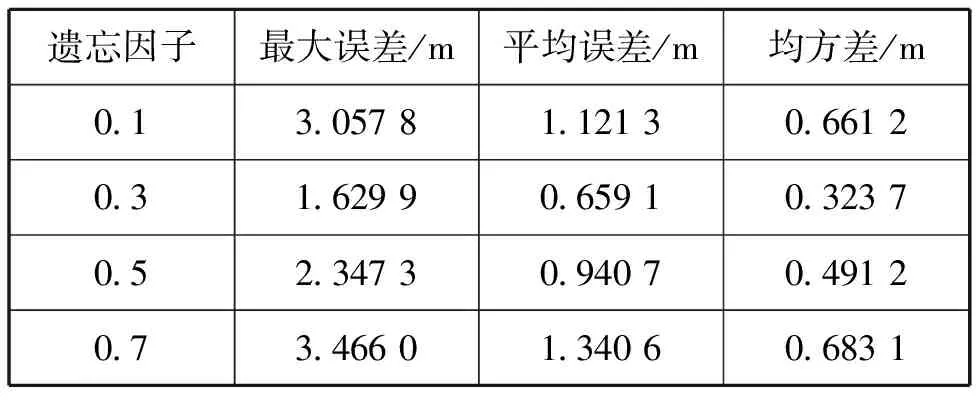
表4 不同遗忘因子定位误差统计

4 结束语

水下精确定位对于基于自主水下航行器的海洋开发任务至关重要。本文针对EKF算法在AUV单信标导航系统中引入线性化误差、定位精度不足等问题,融合多新息理论和遗忘因子,提出基于改进MIEKF的AUV单信标导航定位算法。根据AUV航行特点建立运动模型,基于单信标测距、水流速度建立观测模型。以多新息取代EKF算法中的单新息修正,进一步引入遗忘因子削弱历史数据的饱和现象。通过MATLAB软件进行仿真对比实验,并对初始状态、新息长度和遗忘因子大小对改进算法性能的影响进行了讨论。结果表明,相比于标准EKF算法,改进MIEKF算法最大定位误差减少2.352 2 m,定位误差平均值减少0.856 4 m,意味着改进算法具有良好的定位能力。在相同环境下,新息长度p为6,遗忘因子为0.3时,算法性能最优。