对导弹单脉冲跟踪雷达的交叉眼干扰方法研究

刘佳伟,达通航,房晓明,王 晨,张二涛

(解放军63618部队,新疆 库尔勒 841000)

0 引 言

近些年导弹技术迅猛发展,已成为对重要军事设施的常用打击摧毁手段,导弹导引头主动雷达工作过程中,主动雷达导引头的功能包括窄带搜索、前斜合成孔径雷达(SAR)成像、单脉冲跟踪等工作模式。在被动搜索、窄带搜索、前斜SAR窄带宽带成像匹配之后,对锁定目标使用单脉冲跟踪模式进行持续、稳定的跟踪,单脉冲跟踪过程能够克服强海杂波干扰,对目标的斜距、径向相对速度、角度和角速度进行精确测量,同时单脉冲跟踪对抗舰船目标、雷达车/雷达站目标等释放的各种无源和有源干扰有较强的适应能力,增强了雷达导引头在复杂电磁环境下的跟踪能力,并且具备记忆跟踪能力,可以在单脉冲搜索、大前斜SAR成像之间快速切换工作模式,大大提高了导弹打击效率。

为了对抗导引头单脉冲跟踪,船舶和飞机由于使用情况限制,一般采用舷外干扰、拖拽式干扰、抛洒式干扰,这些干扰往往成本高、效果持续时间短。而交叉眼干扰能够安装在被保护平台上,具有良好的角度欺骗效果,并能起到持续干扰效果。因此双站反向交叉眼系统成为一种有效的对抗单脉冲跟踪模式的手段,各国学者对双站反向交叉眼技术进行了大量的研究。W.P.du Plessis等[1]给出了一般的双站反向交叉眼作用公式,同时给出反向交叉眼系统工程化干扰效果测量方法[2],还对交叉眼干扰的容限问题及路径差对交叉眼增益的影响进行了分析[3-4],Warren du Plessis教授则对交叉眼理论及应用中的其他多个问题进行了研究。文献[5]～[8]给出了双站反向交叉眼的实现和指示角测量的具体构建方法。

刘天鹏[9-10]对交叉眼基本理论及多源反向交叉眼干扰技术问题进行了详细研究,并在文献[11]中对交叉眼干扰理论、系统研制、装备发展等方面对2019年以前的情况进行了综述。周亮[12]等研究了交叉眼干扰机干扰模型对参数的敏感性。刘松杨[13-14]、王彩云[15]、LIU T[16]等在考虑平台反射回波的基础上对双站反向交叉眼干扰展开了研究。同时周伟江[17]仿真了交叉眼对导弹的干扰效果,张福群[18]研究了在无人机电子战中使用拖拽的EWUAV交叉眼干扰装置的干扰效果问题,李栋[19]研究了交叉眼技术对主被动单脉冲雷达测角的干扰效果。

目前国内外对交叉眼系统的理论和应用研究已经非常细致,得出的结论也较为一致。但有些结论却和实际应用中的现象存在一定的出入,并且目前的研究大多局限在交叉眼系统本身引入的指示角上,不能描述交叉眼系统实际的角度欺骗能力,缺少和实际对抗模式结合进行的交叉眼理论和应用研究。

本文首先对双站反向交叉眼进行数学模型建立,分析一般交叉眼数学模型建立过程中的基本假设、近似误差来源及其误差大小,给出交叉眼系统引入的指示角随各变量的正确变化关系,分析对抗场景中布站方式对双站反向交叉眼干扰效果的影响,最后结合具体对抗场景给出了在对抗导弹单脉冲跟踪雷达的过程中交叉眼干扰的使用场景和建议。

1 双站反向交叉眼基本关系分析

交叉眼干扰技术是目前工程应用中最主要的角度欺骗技术。如图1所示,敌方雷达发射的探测脉冲被干扰站1接收,干扰站1将接收到的信号传输给干扰站2,由干扰站2辐射出去。干扰站2接收到的探测脉冲被移相180°之后传送给干扰站1,由干扰站1辐射出去。由于2个信号走过的路径完全相同,因此由波程差引起的相位偏移可以忽略不计,通过控制其中1路信号的相位就可以控制2路信号在敌方雷达处叠加相位,2路信号在敌方雷达处合成就形成扭曲的磁场,从而形成失真的波前,产生欺骗角度。

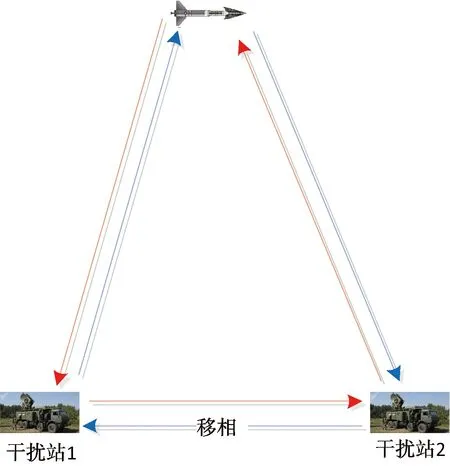
图1 双站交叉眼工作示意

双站反向交叉眼和雷达位置关系及角度标注如图2所示,其中雷达天线尺寸为dr,2个交叉眼单元之间的距离为dc,交叉眼系统到雷达的距离为r,雷达天线指向对交叉眼系统中心的夹角为θr,交叉眼波束中心到雷达的指向角为θc,雷达到上下交叉眼单元与到交叉眼系统中心的夹角分别为θe1和θe2,由交叉眼系统引入的指向角为θi。

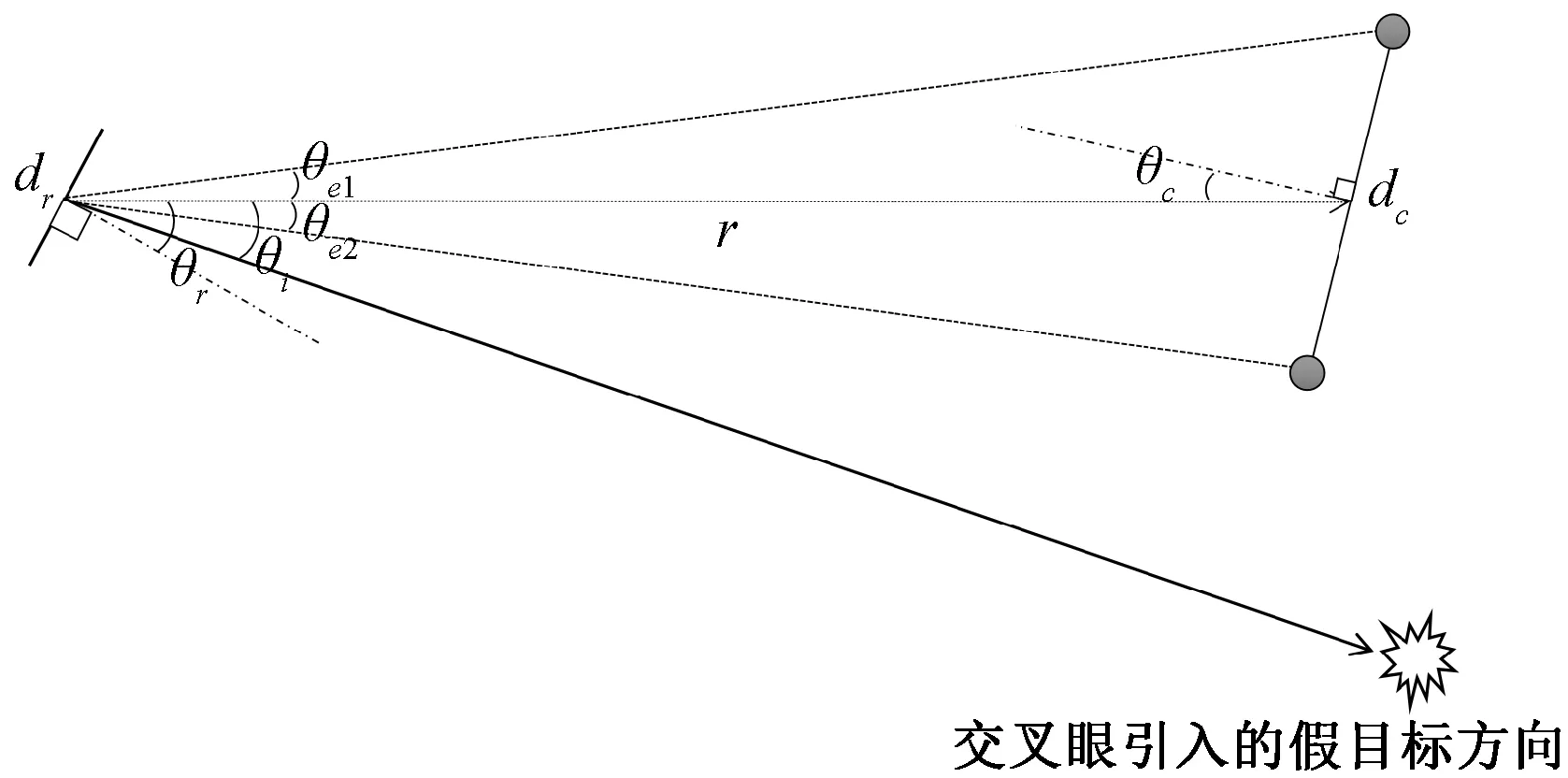
图2 交叉眼和雷达位置关系及角度标注

根据图2所示的位置关系及角度标注,建立双站反向交叉眼对雷达干扰的精确数学模型(多站情况的分析过程类似),在考虑实际情况下引入近似,得到一种形式较为简单的近似理论表达式。雷达到上下交叉眼单元与到交叉眼系统中心的夹角θe1,2可表示为:

(1)

同时假定r>>dc,则上式可以简化为:

(2)

交叉眼系统上下单元信号在雷达天线上的和差通道中分别为:

(3)

(4)

式中:Pr表示雷达的天线方向图;β=2π/λ代表波数,因为θe较小,因此可做如下近似:

(5)

(6)

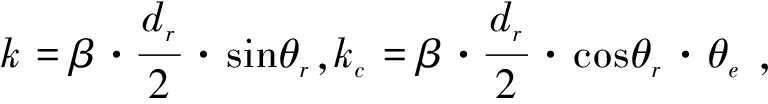
S1,2=Pr(θr±θe)cos[k±kc]

(7)

D1,2=Pr(θr±θe)sin[k±kc]

(8)

设交叉眼单元2转发到单元1的信号和单元1转发到单元2的信号幅度比为a,相位差为φ,根据信号流程得到雷达接收的和差通道的信号分别表示为:

Sr=S1Pc(θc+θe)S2Pc(θc-θe)+

aejφS2Pc(θc-θe)S1Pc(θc+θe)

(9)

Dr=S1Pc(θc+θe)D2Pc(θc-θe)+

aejφS2Pc(θc-θe)D1Pc(θc+θe)

(10)

式中:Pc表示交叉眼单元的天线方向图,使用三角函数关系式可将上面两式写为:

Sr=Pr(θr+θe)Pc(θc+θe)Pr(θr-θe)Pc(θc-θe)·

(11)

Dr=Pr(θr+θe)Pc(θc+θe)Pr(θr-θe)Pc(θc-θe)·

(12)

在雷达的单脉冲测角过程中一般取差和通道比值的实部进行,由式(11)和式(12)可得差和通道比值的实部为:

(13)

对雷达的单脉冲测角来说,散射源回波的和差通道比值的实部为:

(14)

由式(13)、式(14)可得交叉眼系统引入的雷达指示角为:

(15)

至此,得到了双站反向交叉眼引入的雷达指向角和各要素之间的关系。

2 双站反向交叉眼干扰效果影响因素分析

本节将对双站反向交叉眼近似数学模型和精确数值解进行比较,分析近似数学模型的精度,研究数学模型中近似误差的影响。然后基于精确数值解给出不同变量对交叉眼干扰效果的影响。

2.1 数学模型中的近似误差

式(13)的推导过程中首先假定r>>dc,对tan(θe)的表达式进行了近似,之后又在推导和差通道的表达式中进行了cosθe≈1,sinθe≈θe的近似,为了衡量这种近似对最终结果的影响,将使用式(13)得到的指向角和未进行近似的数值解得到的指向角进行对比。

首先设雷达波束宽度为10°,对应2个2.54倍波长的线源,间隔dr=2.54λ,2个交叉眼单元之间的距离dc=100 m,交叉眼波束中心到雷达的指向角θc=10°,幅度比a=0.944 1,相位差φ=179°,在不同距离r上,以雷达波束指向对交叉眼系统中心的夹角θr为自变量,分别计算出由式(13)和未近似的数值解得出的交叉眼系统引入的指向角之差,如图3所示。相位差为φ=179°,距离r=10 km,在不同幅度比a下的结果如图4所示。幅度比a=0.944 1,距离r=10 km,在不同相位差φ下的结果如图5所示。幅度比a=0.944 1,距离r=10 km,相位差φ=179°,在不同交叉眼单元距离dc下的结果如图6所示。

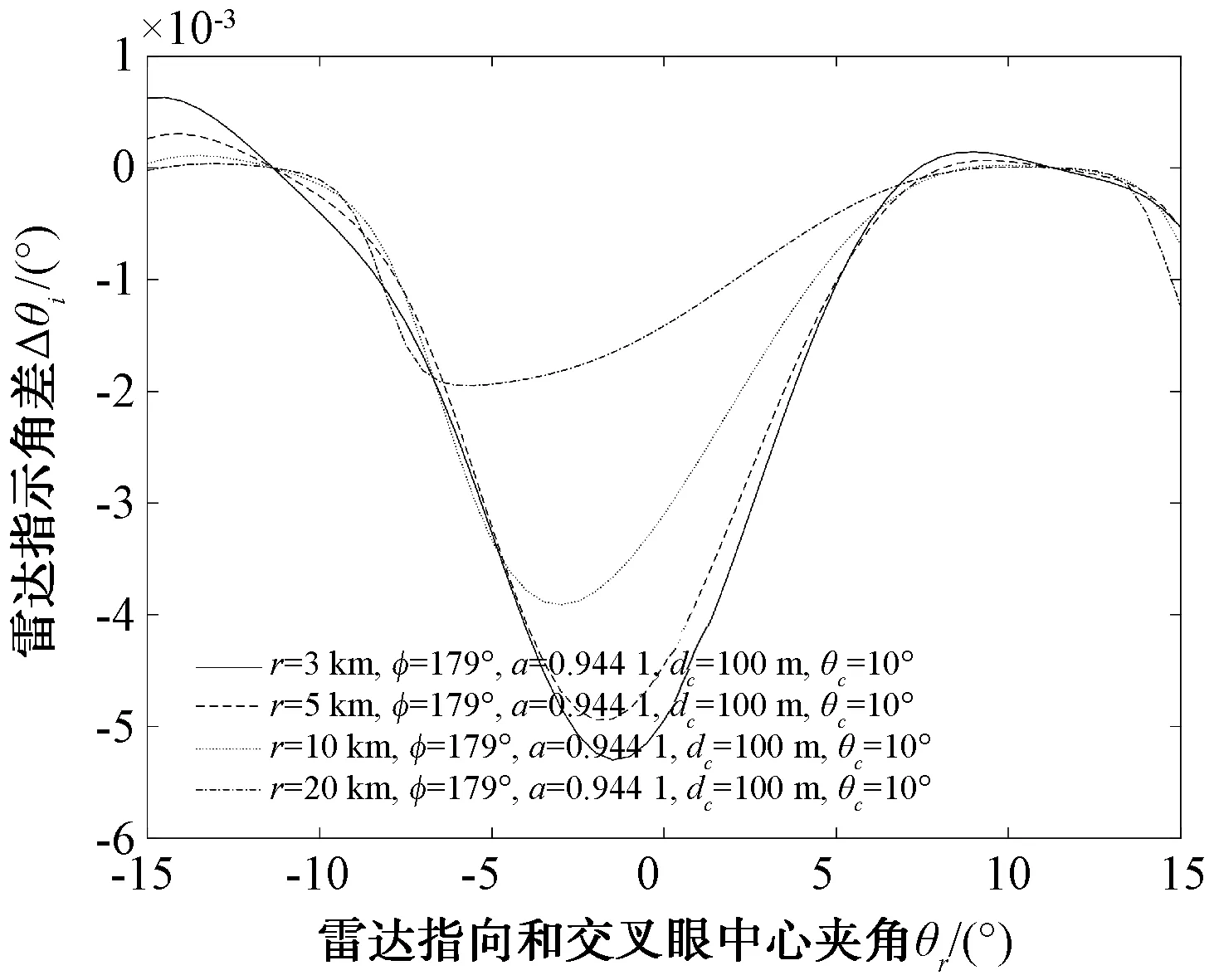
图3 不同干扰距离近似方程解和数值解差值

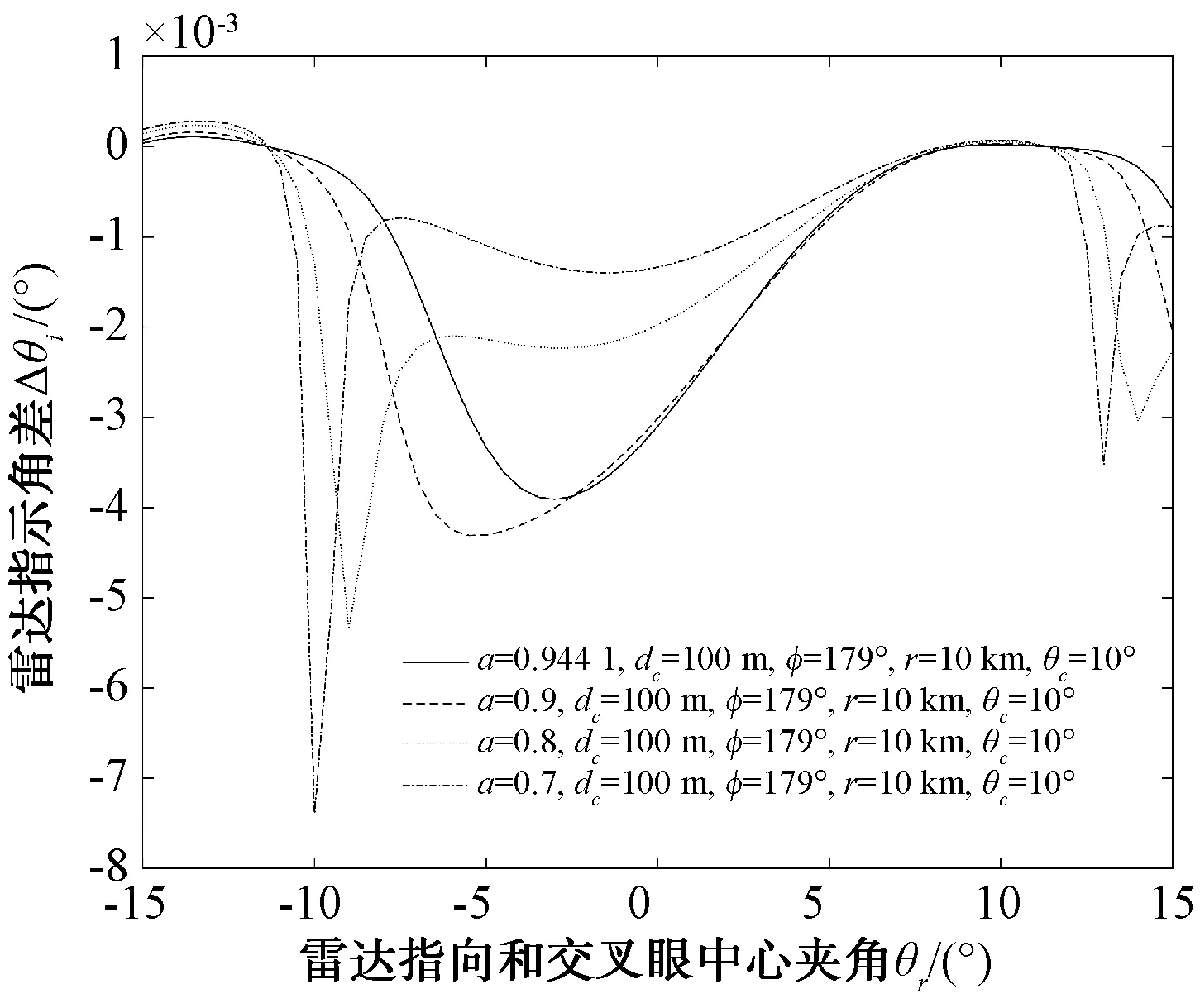
图4 不同幅度比近似方程解和数值解差值

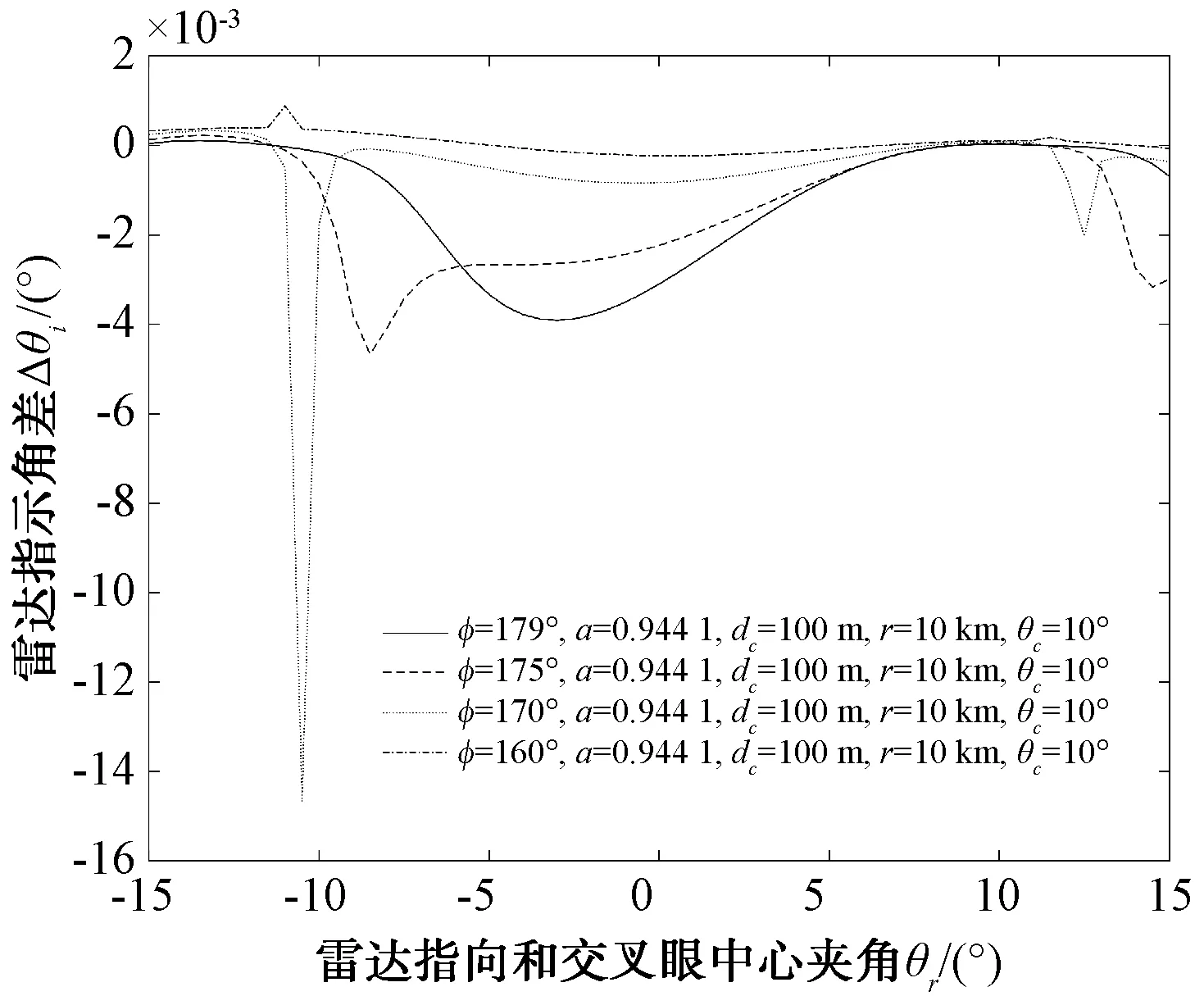
图5 不同相位差近似方程和数值解差值

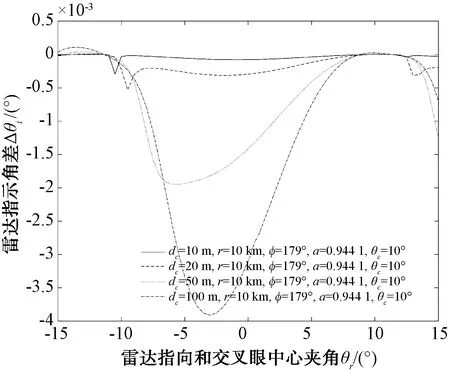
图6 不同交叉眼单元距离近似方程和数值解差值

从图3～图6结果来看,近似解和数值解之间的误差随着干扰距离r的增大而逐渐变小,随幅度比接近1误差减小,随相位差接近180°而增大,随dc增大而增大,在交叉眼常用参数下整体误差较小,因此在分析交叉眼性质时使用推导的近似数学模型不会存在较大误差。

2.2 双站反向交叉眼增益

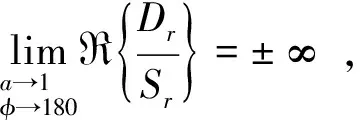
交叉眼增益Gc对a和φ的一阶导数分别为:

(16)

(17)

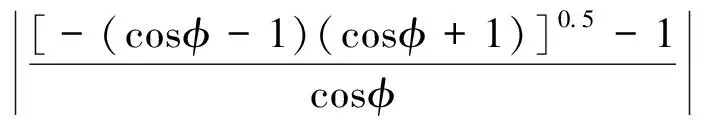
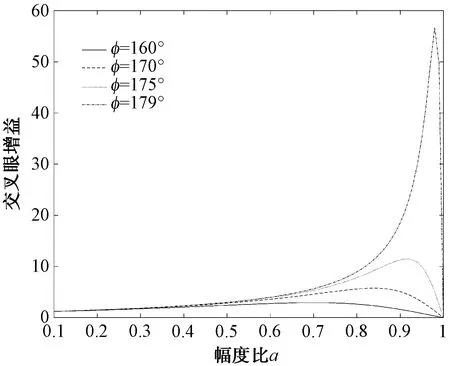
图7 交叉眼增益随幅度比变化

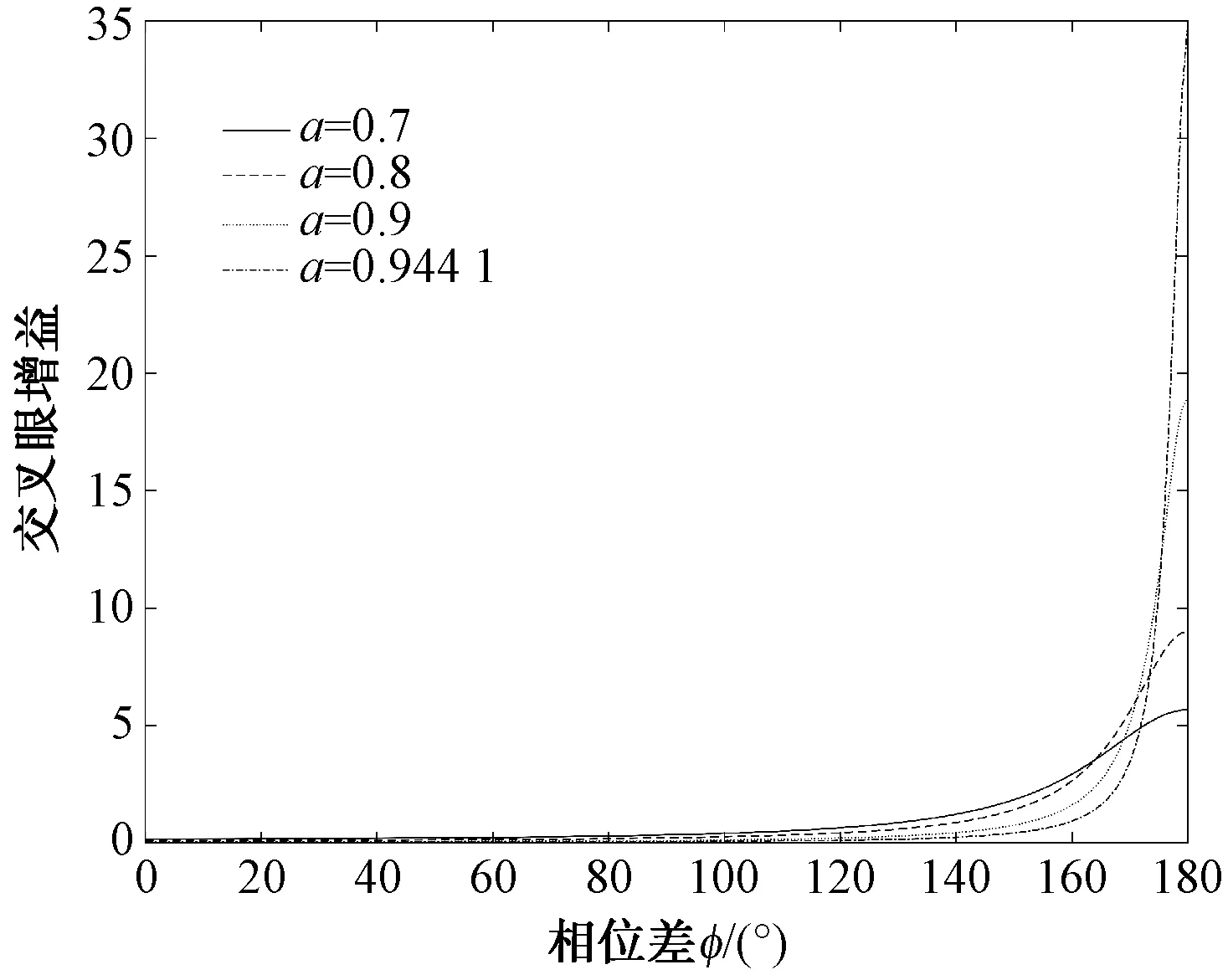
图8 交叉眼增益随相位差变化

2.3 各因素对交叉眼系统角度欺骗效果的影响

对交叉眼干扰效果具有影响的变量主要包括2个交叉眼单元信号幅度比、相位差、雷达到交叉眼系统距离及2个交叉眼单元之间的距离,图9～图10相应展示了上面4个因素对交叉眼系统引入的雷达指示角的影响。

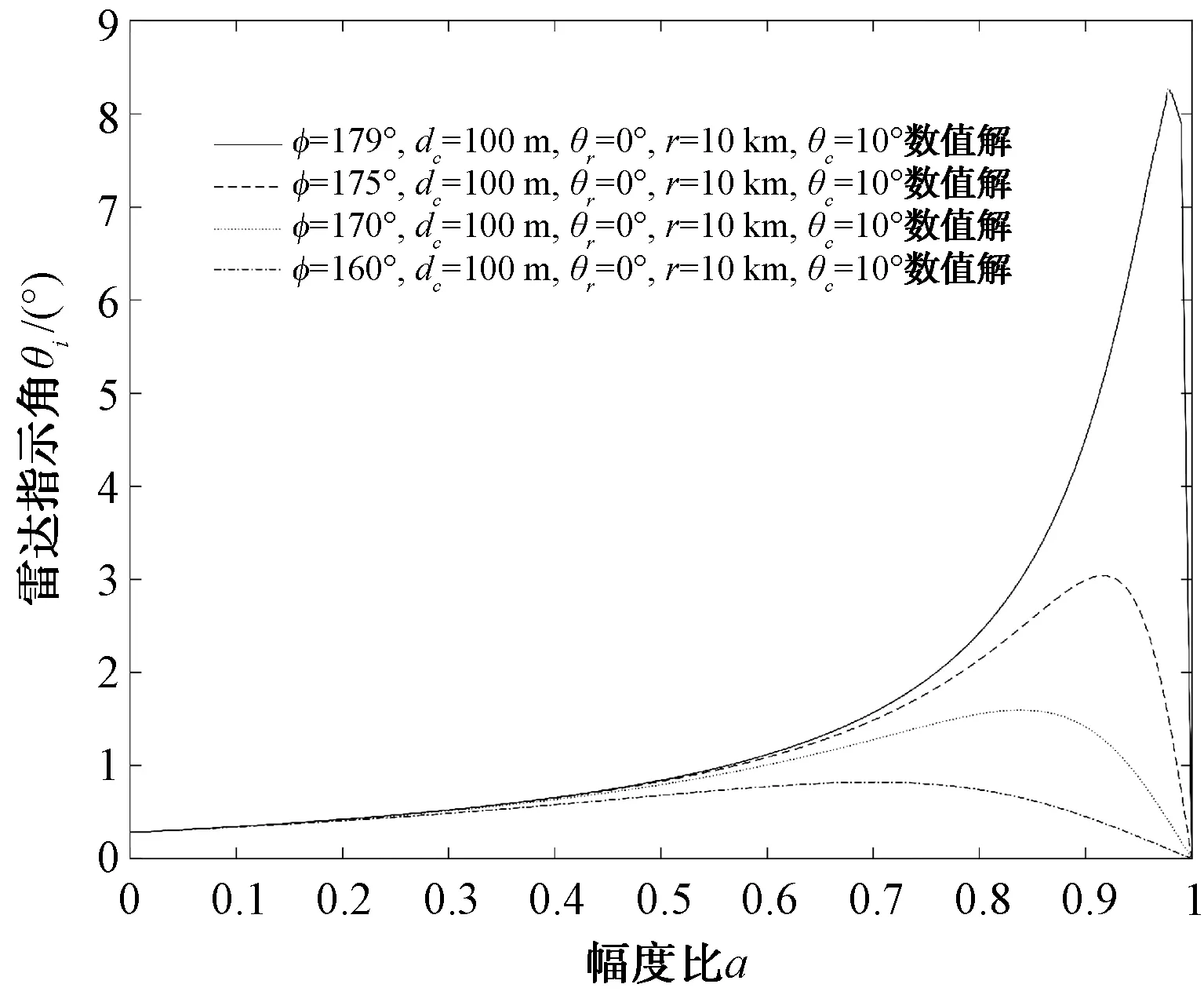
图9 雷达指示角随幅度比变化

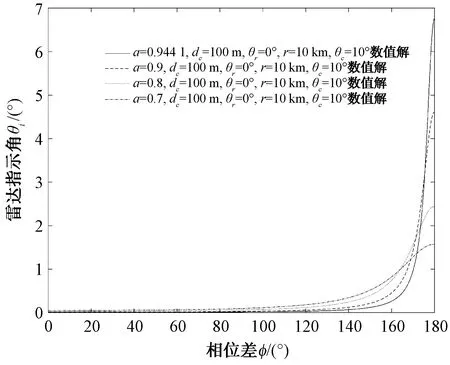
图10 雷达指示角随相位差变化

将图9、图10和图7、图8进行对照来看,定义的交叉眼增益能够较为准确地对交叉眼系统引入的指示角进行描述,且交叉眼增益在幅度比变量上有极值存在,而图9、图10表明交叉眼系统引入的指示角同样随幅度比变化有极大值存在。

对于交叉眼干扰系统来说,2个单元相位差φ越接近180°,导弹到干扰机距离r越近,干扰单元之间的间隔dc越大,则其引入的指示角偏离雷达指向和交叉眼中心夹角θr的程度越大(如图9、图11、图12所示)。但引入的雷达指示角随幅度比不是单调递增的,而是在值为1前存在极大值点,极值点位置随2个单元信号相位差φ的不同而不同,这点需要在使用交叉眼系统过程中注意。

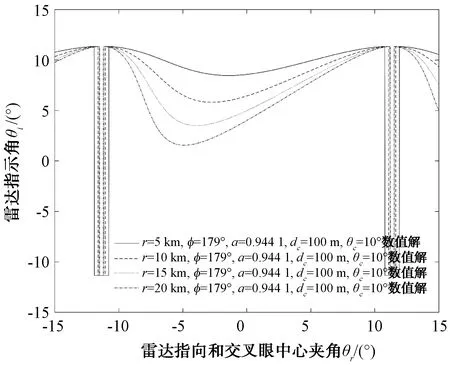
图11 不同干扰距离下雷达指示角

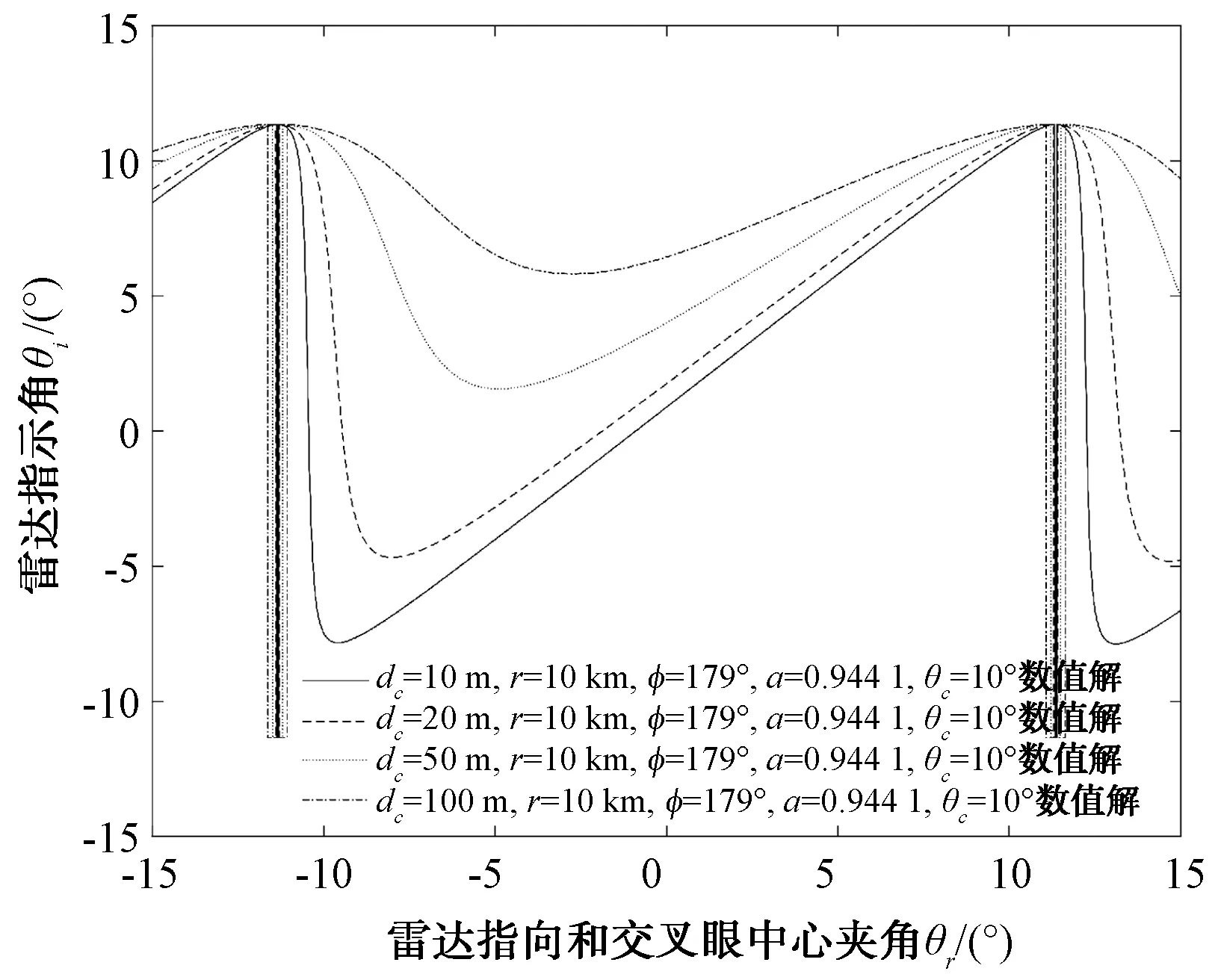
图12 不同交叉眼单元间距下雷达指示角

交叉眼干扰效果的影响因素比较多,并且相互之间是强耦合关系,独立分析其中单一因素难以获取有效信息,信号幅度比和信号相位差对交叉眼系统引入的雷达指示角的关系如图13、图14所示,在实际使用时需根据需求提前做好规划。

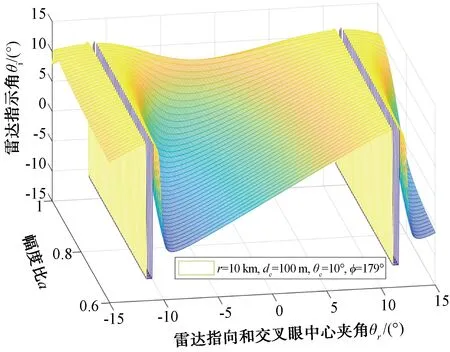
图13 θr-a-θi关系

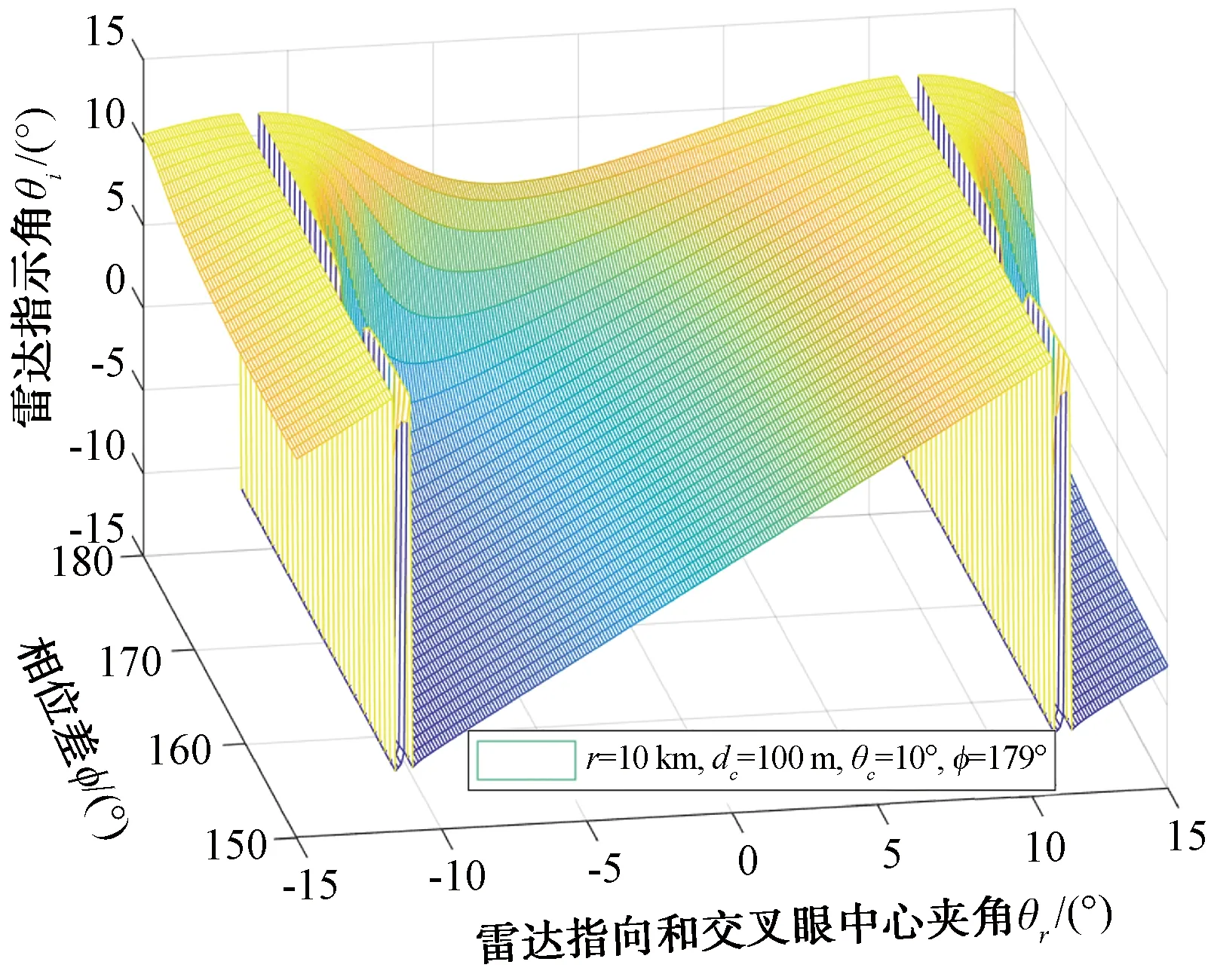
图14 θr-φ-θi关系

3 双站反向交叉眼典型使用场景及干扰效果仿真

以装备对抗具备单脉冲跟踪模式的导引头为例,研究对抗导弹单脉冲跟踪雷达的作战场景及干扰系统的使用建议。

3.1 导引头单脉冲跟踪工作模式及对抗布站

假设导引头工作时序为:当弹目距离约为20 km时,导引头进入纯单脉冲跟踪模式,弹目距500 m进入导引头雷达盲区,导引头雷达关机。雷达单脉冲跟踪处理一般流程如图15所示。

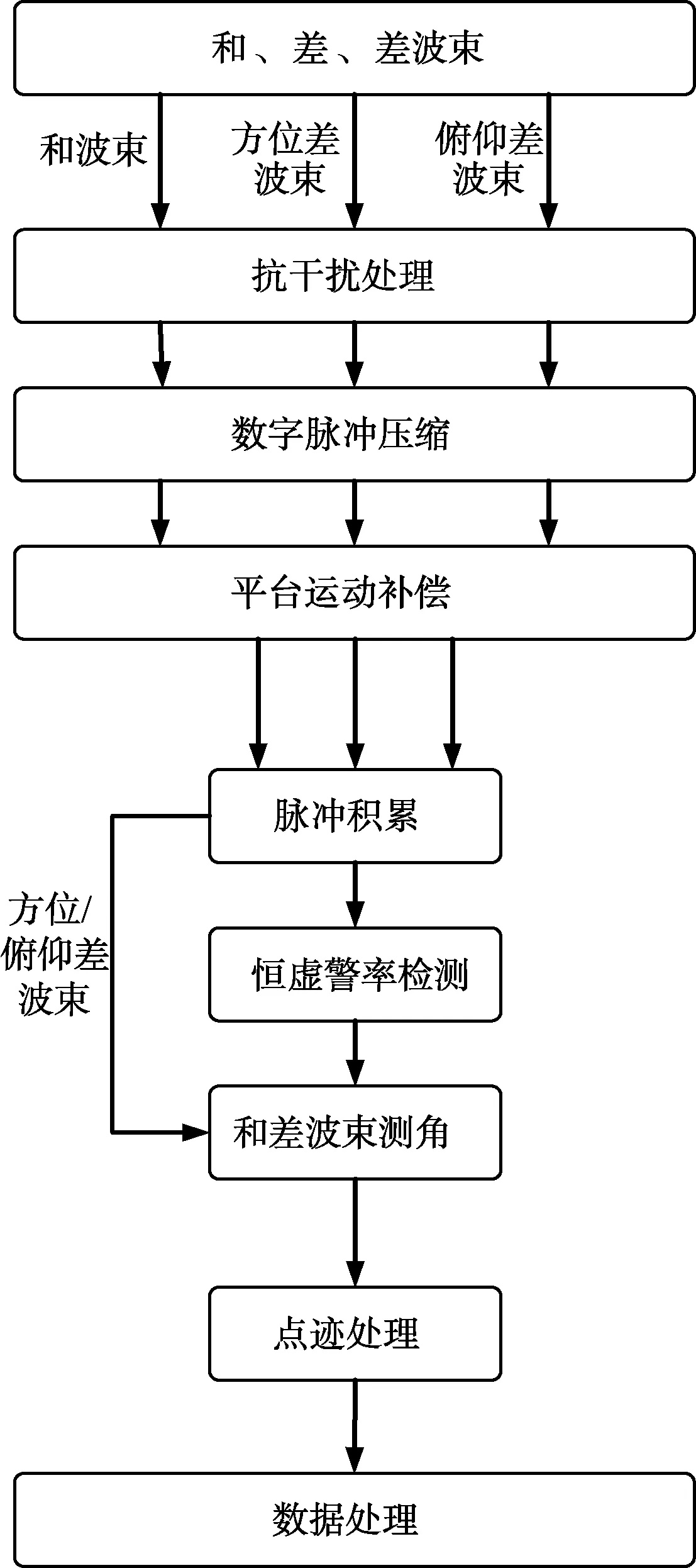
图15 雷达单脉冲跟踪处理流程

目标的回波信号和交叉眼干扰信号难以存在稳定的相位关系,因此不将目标回波和交叉眼信号一同分析。假设目标回波和交叉眼信号在雷达同一角度分辨单元内,则要求交叉眼信号显著大于目标回波才能起到较好的干扰效果,若交叉眼信号和目标回波不在同一个雷达距离分辨单元内,则要求交叉眼信号强于目标回波。

根据以上分析,双站反向交叉眼的布站方式至少有2大类:随队式和支援式。随队式干扰是将2个干扰站布设在保护目标的同一阵地上,或被保护目标上(如船舶、飞机等),一般是将干扰站布设在被保护的目标两侧(如图16),以尽量拉开2个干扰站的距离。支援式干扰是将交叉眼系统布设于被保护目标的阵地外(图17),此时要考虑干扰机位置和导弹雷达波束之间的位置关系,保证2个交叉眼单元的信号能够同时进入导引头雷达接收机。为了保证干扰系统信号接收及发射,一般使用随队干扰,在已知导弹来袭方向或不具备随队干扰条件时才使用支援干扰。

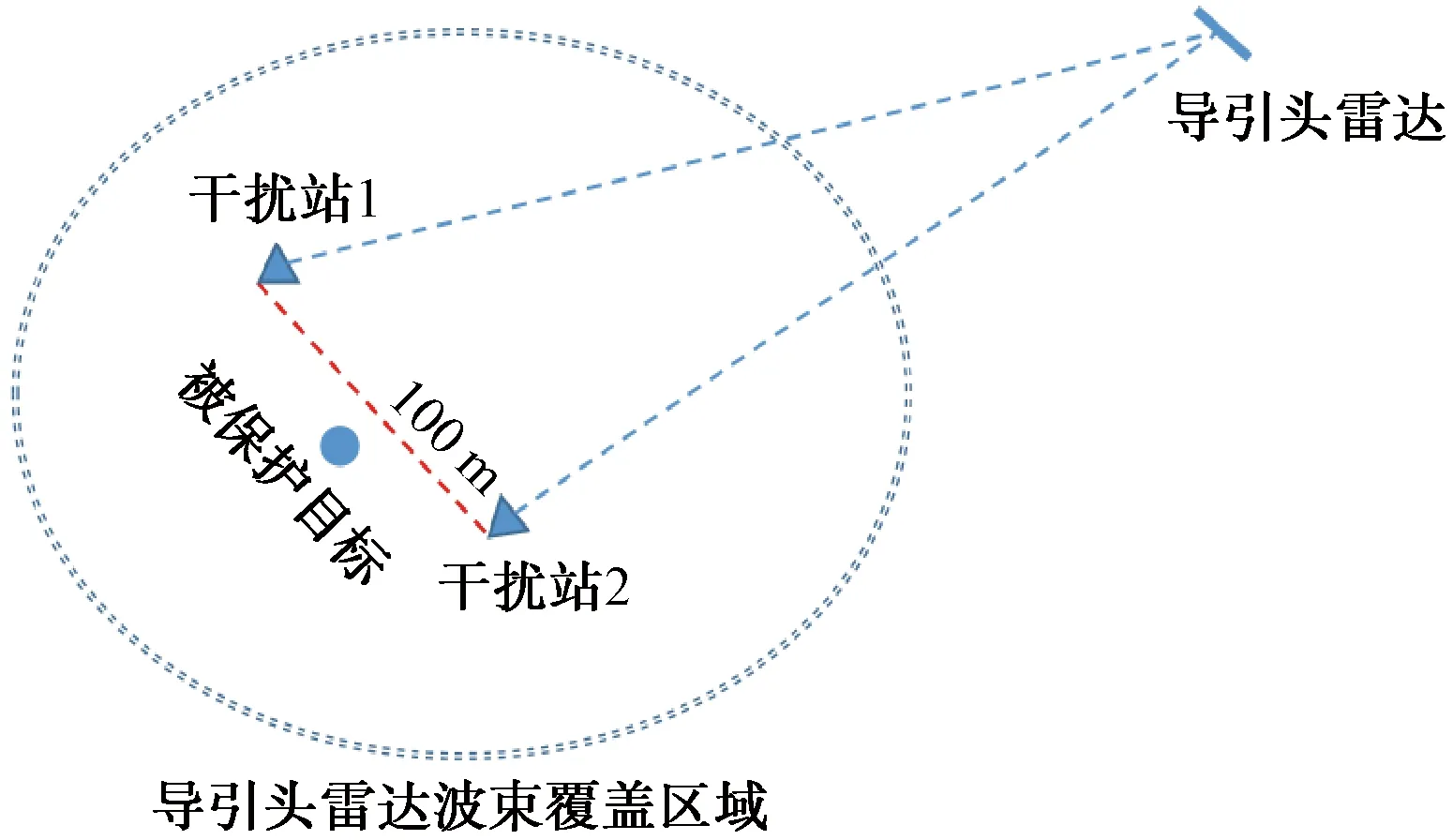
图16 随队干扰情况

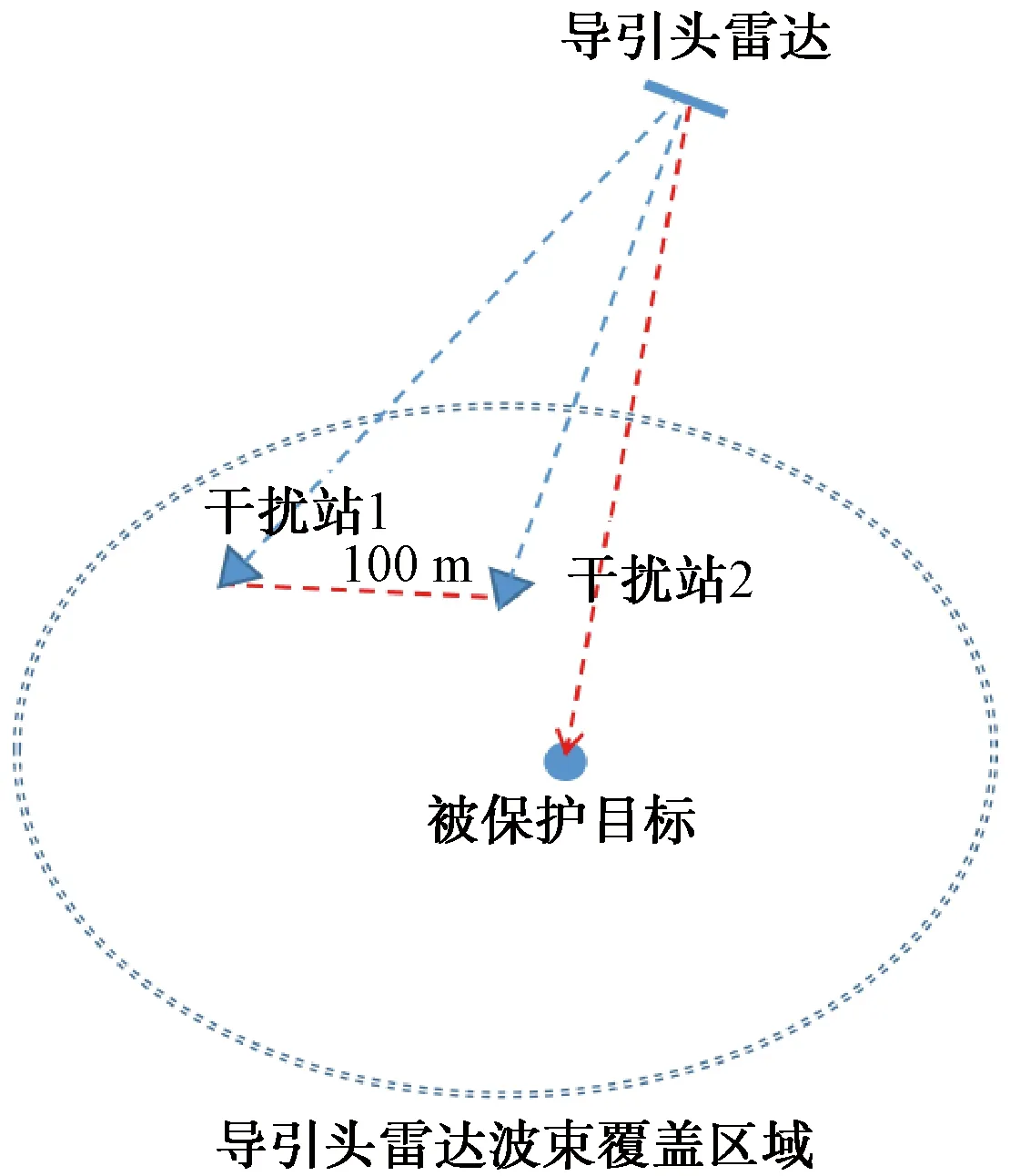
图17 支援干扰情况

以上的分析都是针对雷达指示角θi进行的,雷达指示角θi表征了在不同雷达指向θr时交叉眼系统使雷达测量角度偏离交叉眼系统几何中心的能力,这一能力并不能直接用来衡量交叉眼系统在对抗过程中的角度欺骗能力,具体角度欺骗能力还与对抗场景相关。在随队干扰情况下,若被保护目标在交叉眼系统中心,引入的雷达指示角越大则雷达指向越偏离真实目标,角度欺骗效果越强。在支援干扰情况下则应该综合考虑雷达指示角和被保护目标相对于干扰系统中心的位置关系来确定角度欺骗效果。

3.2 干扰效果仿真

假定雷达初始指向其探测到的真实目标,雷达指向和交叉眼系统中心夹角为θr0=-5°,此时交叉眼干扰系统开机,假设交叉眼系统引入了1个指向角θi,并且在和通道中的信号强度超过目标回波,简化引导率认为雷达在下一时刻指向θi/2,即θr=θi/2作为下一时刻的雷达指向。在此假定下,给定导弹雷达运动轨迹,就可以对雷达指向角进行迭代计算。进一步简化计算,假定导弹到干扰系统的距离是线性变化的,且飞行过程中θc保持不变,计算导弹雷达目标指示角的变化情况,如图18所示。可以看出,交叉眼干扰系统对导引头雷达引入的指示角在1个周期内是一个发散过程,对随队干扰来说,只要将2个交叉眼信号幅度稳定控制在0.8、相位差控制在160°,在干扰机间隔100 m时能够获得持续变大的引偏角度。对支援干扰来说则要避免交叉眼引入的雷达指示角恰好指向目标,在使用时可以根据预估的导弹轨迹对交叉眼的干扰效果进行预估。

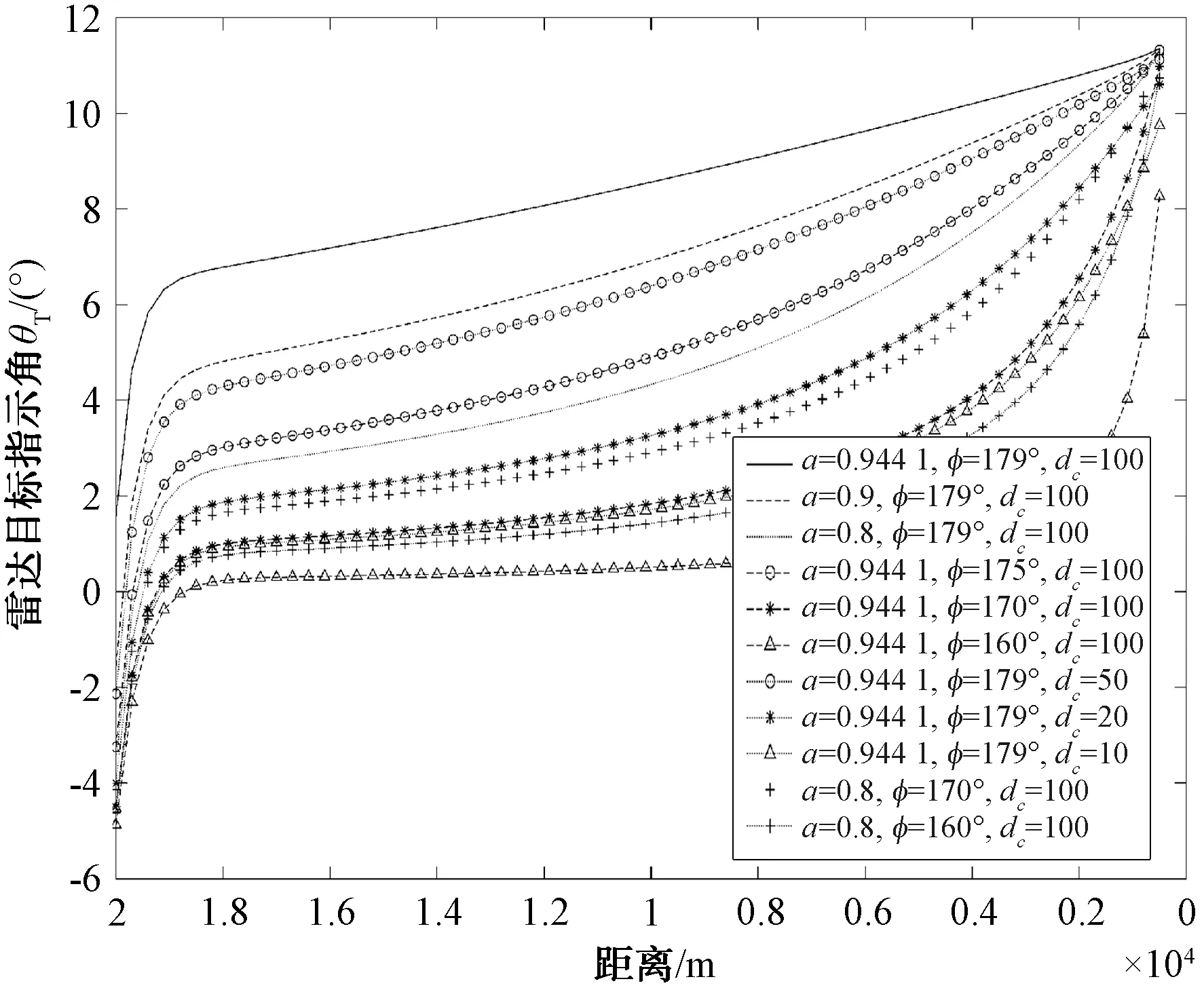
图18 θr0=-5°雷达目标指示角随弹干距的变化

4 结束语

本文推导了双站反向交叉眼系统对雷达系统的指示角数学模型,并基于近似得到了交叉眼常用数学表达式,分析了近似误差带来的影响,结合使用场景分析了影响交叉眼干扰系统的各因素,得出如下结论:

(1)常用的近似数学表达式和精确数值解之间误差较小;交叉眼关系表达式及交叉眼增益表达式可以对交叉眼干扰和各因素的关系进行正确的描述;交叉眼引入指示角是周期性变化的。

(2)2个干扰站之间的相位差越接近180°,引入的雷达指示角越大;雷达指示角随幅度比不是单调变化的,而是存在极大值点,并且相位差越接近于180°,极值点位置越接近1,因而使用时并非幅度比越接近1引入的雷达指示角越大,还需结合相位差分析;干扰距离越小引入的指示角越大;2个干扰机距离越大,引入的指示角越大。

(3)随队干扰情况下,若被保护目标在交叉眼系统中心,引入的雷达指示角越大则角度欺骗效果越强;在支援干扰情况下则应该综合考虑雷达指示角和被保护目标相对于干扰系统中心的位置关系来确定角度欺骗效果。

(4)交叉眼干扰系统引入的雷达指示角在1个周期内是发散的,只要能稳定控制相位和幅度差在一定的范围,就可以持续对导引头单脉冲跟踪系统进行角度拖引。