高光谱微波亮温数据预处理方法分析

关 鑫

(中国船舶集团有限公司第八研究院,江苏 扬州 225101)

0 引 言

大气温度廓线即温度在大气中的垂直分布,是大气状态参数十分重要的组成部分,其在气象预报、极端天气预警和气象分析等研究领域有着重要作用[1]。目前在轨的微波温度辐射计一般只有几个到十几个通道,根据每个通道的权重函数,单个通道只能较为精确地探测很小的一段垂直大气中的温度,所以想要进行精细的大气垂直探测几乎不可能实现。在此背景下,发展高光谱微波辐射计成为了一种趋势。

由于高光谱探测卫星上的探测通道非常多,通常有几千个,所以其测量数据十分庞大。而这产生了一些新的问题:一是计算量太大;二是数据会携带很多冗余信息,这将增加数据传输、存储的成本,同时也会对反演精度有一定影响。通过对高光谱数据进行预处理可以大大减少其数据量,从而解决这些问题。

神经网络方法在大气温度廓线反演方面已经有了非常广泛的应用。1994年Churnside等人首次使用神经网络反演法以NWS的无线电探空仪历史数据为基础对大气温度垂直分布进行了反演[2]。2005年Karbou等人使用神经网络反演方法对AMSU探测的晴空亮温数据进行了地表为陆地情况的大气温湿度垂直分布反演[3]。1999年Frate等人用五层神经网络方法反演了大气温度廓线[4]。

本文根据SeeBorV5.0数据集中的大气温湿度廓线,使用MPM93的正演模型产生频率范围为50～60 GHz、通道数为2 000的高光谱仿真亮温数据。分别使用主成分分析法和通道选择方法2种方法对仿真亮温数据进行预处理。将处理过后的数据作为神经网络的输入对大气温度廓线进行反演。比较2种预处理方法对神经网络反演结果精度的影响,并说明2种预处理方法各自的优劣。

1 研究方法

本文所用的原始数据来自全球晴空大气廓线训练数据集(SeeBorV5.0),其中包括分布在全球范围的15 704条晴空条件下的温度、湿度廓线。从其中随机挑选出10 000条大气温湿度廓线作为主要的实验数据。使用MPM93吸收系数模型来计算吸收系数,再利用辐射传输方程得到对地观测的仿真亮温。

本文的实验流程框图如图1所示。首先选择数据预处理的方法,是进行主成分分析还是进行通道选择来预处理亮温数据。之后设置预处理方法的条件,主成分分析主要是设置选取主成分的个数,通道选择主要是设置要选择的通道个数。最后对经过预处理的数据进行神经网络反演并对反演结果进行分析。

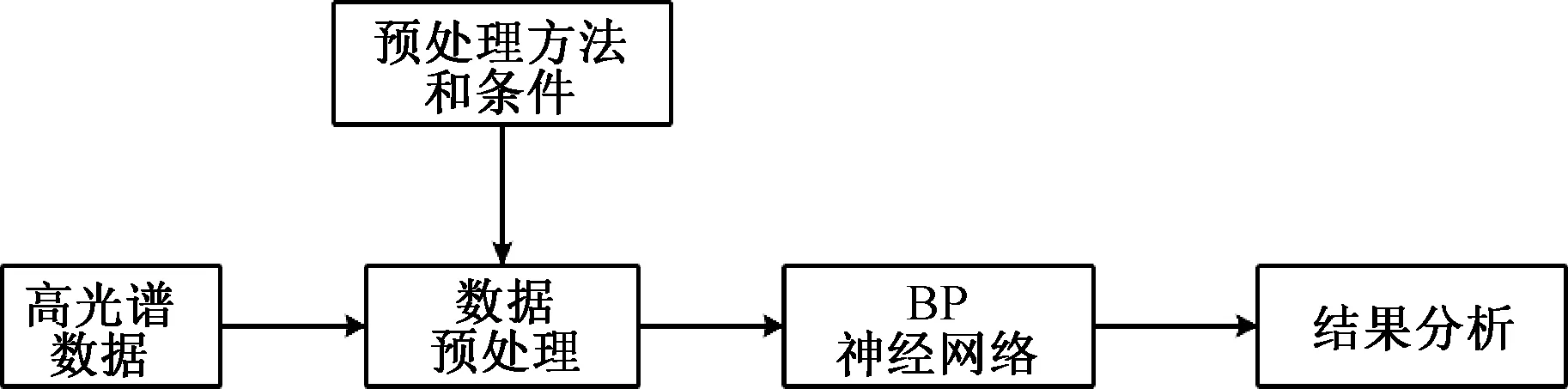
图1 实验流程框图

1.1 主成分分析

对通过正演模型计算得到的高光谱仿真亮温数据做主成分分析,结果如图2所示。图中横坐标为主成分的序列号,如1代表第一主成分,纵坐标是主成分对应的特征值占总样本数据特征值的百分比,直方图代表各主成分的特征值占总特征值的百分比,折线图表示前n个主成分的特征值占总特征值的百分比。由图2可以看出只取前5个主成分时其特征值的和就可以占总特征值的98.42%,取前10个时可以达到99.12%,所以理论上取10个以内的主成分就可以代表样本中绝大部分的信息特征,从而满足反演的需求。

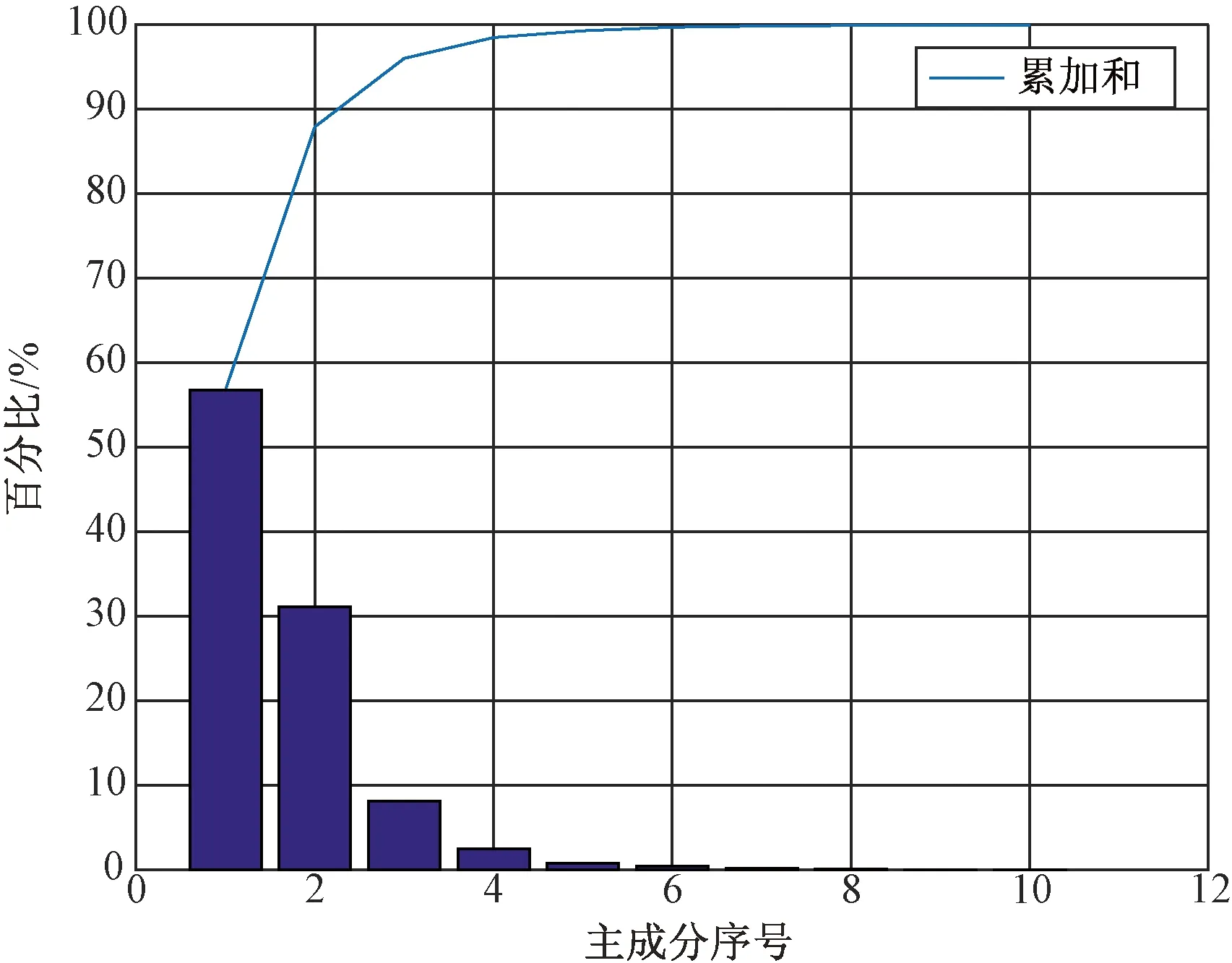
图2 高光谱仿真亮温数据的主成分分析

1.2 通道选择

对高光谱亮温数据进行预处理的另一种方法就是通道选择。通道选择顾名思义就是从所有的探测通道中选出可以代表整体数据的少量通道,在不影响反演精度的情况下尽可能减小数据量。为了更好地评价反演效果,定义大气可反演指标p[5]:

(1)

式中:Sa为背景场误差协方差矩阵;S为反演结果的误差协方差矩阵;p为对反演结果的整体评估。

反演结果的误差协方差矩阵为:

S=Sa-SaKT(Sε+KSaKT)-1KSa

(2)

式中:K为权重函数矩阵;Sε为观测误差协方差矩阵。

当只选择1个通道时,若行向量k表示权重函数矩阵中此通道的权重函数,sε为观测误差协方差矩阵对角线上该通道对应的误差标准差,sε为标量。由式(2)可得,使用此通道进行反演时的误差协方差矩阵是:

S=Sa-SakT(sε+kSakT)-1kSa

(3)

计算出每个通道的p值,并将p值最大的通道作为本次通道选择选出的通道。然后使用式(3)计算出本次选择出的通道S,将其作为下一次迭代的背景场误差协方差矩阵Sa,再将剩下的通道作为下次迭代的选择样本。重复以上步骤即可选出需要的M个通道。

频率范围为50～60 GHz,通道数为2 000的权重函数矩阵如图3所示。对其进行通道选择,设置通道选择的通道数为100,图4为进行通道选择过程中每次迭代选出的通道的权重函数矩阵,可以看出选中的通道的权重函数峰值所在高度基本上可以覆盖从地表到大气高层。

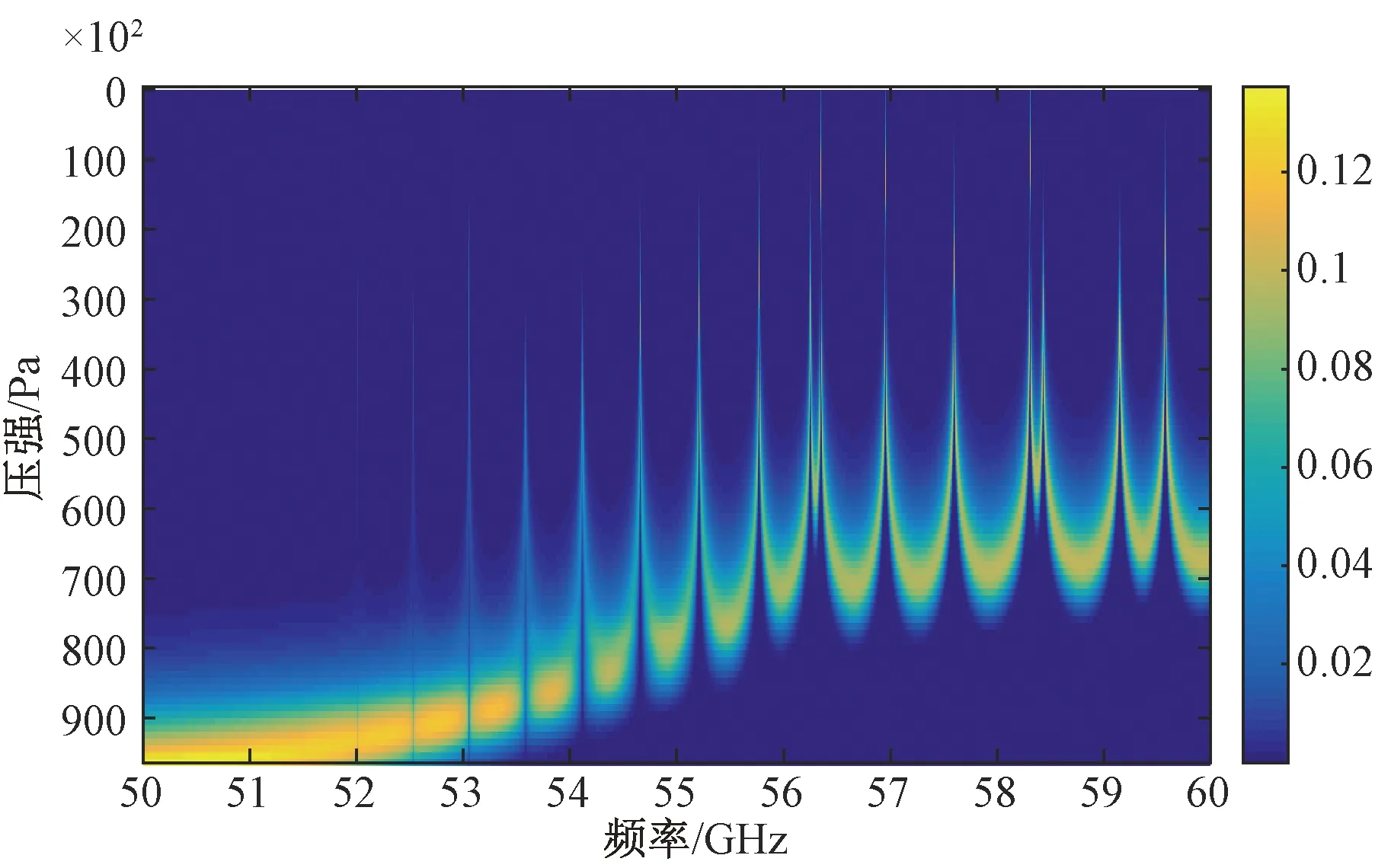
图3 通道数为2 000的权重函数

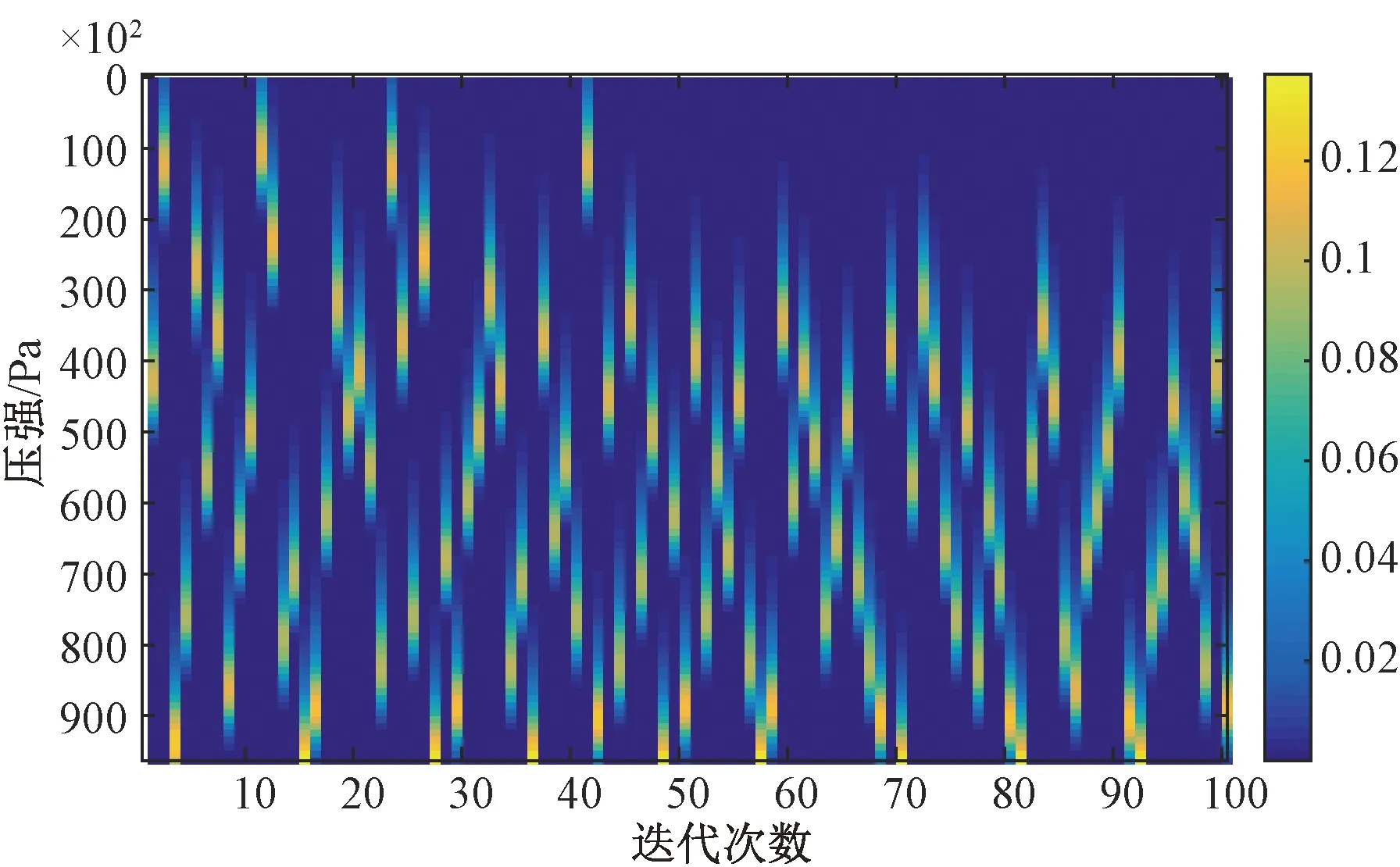
图4 按选中通道顺序的权重函数分布

1.3 神经网络设计

本文使用一个3层的BP神经网络作为大气温度廓线反演的反演模型,其结构如图5所示。由于大气反演的非线性,所以隐层使用双极性S函数作为激活函数来对应此非线性,输出层采用线性激活函数来对应大气温度的动态分布。反演过程可以分为以下几步:(1)将数据分为训练集和测试集,训练集和测试集的生成视实际情况而定;(2)对输入的高光谱数据进行预处理,可以选择主成分分析和通道选择方法,以减少输入个数并消除其相关性;(3)设计网络和合适的训练目标,完成训练。最后通过测试集来进行网络测试,计算网络输出的数据与原始数据的均方根误差。

图5 3层BP神经网络示意图

对BP神经网络的设计主要是对隐层层数、各隐层对神经元个数、学习效率、训练次数和训练目标的设置。经过试验对比,对于大气温度廓线反演只需要单隐层就可以满足要求。隐层中神经元个数参考公式为:

(4)

式中:n表示输出神经元个数;m表示输入单元数;a为1～10之间的常数。

本实验将2～105Pa范围内的大气分为100层,即输出神经元数目为100,而作为神经网络输入的经过预处理后的高光谱数据维数根据预处理方法的不同一般取30～80之间,所以将隐层中神经元个数设置为15。学习效率应设为较小的值,因为较大的值虽然会在开始时加快收敛速度,但在临近最佳点时,可能会无法收敛,所以学习效率一般设置为0.01。对于训练次数和训练目标而言,这两方面相互影响,其数值视具体情况设置。

2 仿真测试实验

对于5 000个样本,按照4∶1的比例随机分配训练集,使用BP神经网络对大气温度廓线进行反演。

2.1 主成分分析实验

将使用不同主成分数量处理后的高光谱亮温数据使用神经网络方法进行反演,其结果如图6所示。图6表示主成分数量为5、10、20、30、40、50、60、70时温度廓线反演结果的均方根误差。

由图6可以看出,主成分的数目为10时相比数目为5时反演精度有很大的提高,主成分的数目为20时相比10时反演精度也有较大的提高;之后继续增加主成分的数目对反演精度的提高相当有限,当主成分数目取到70时反演精度只有微小的提高。

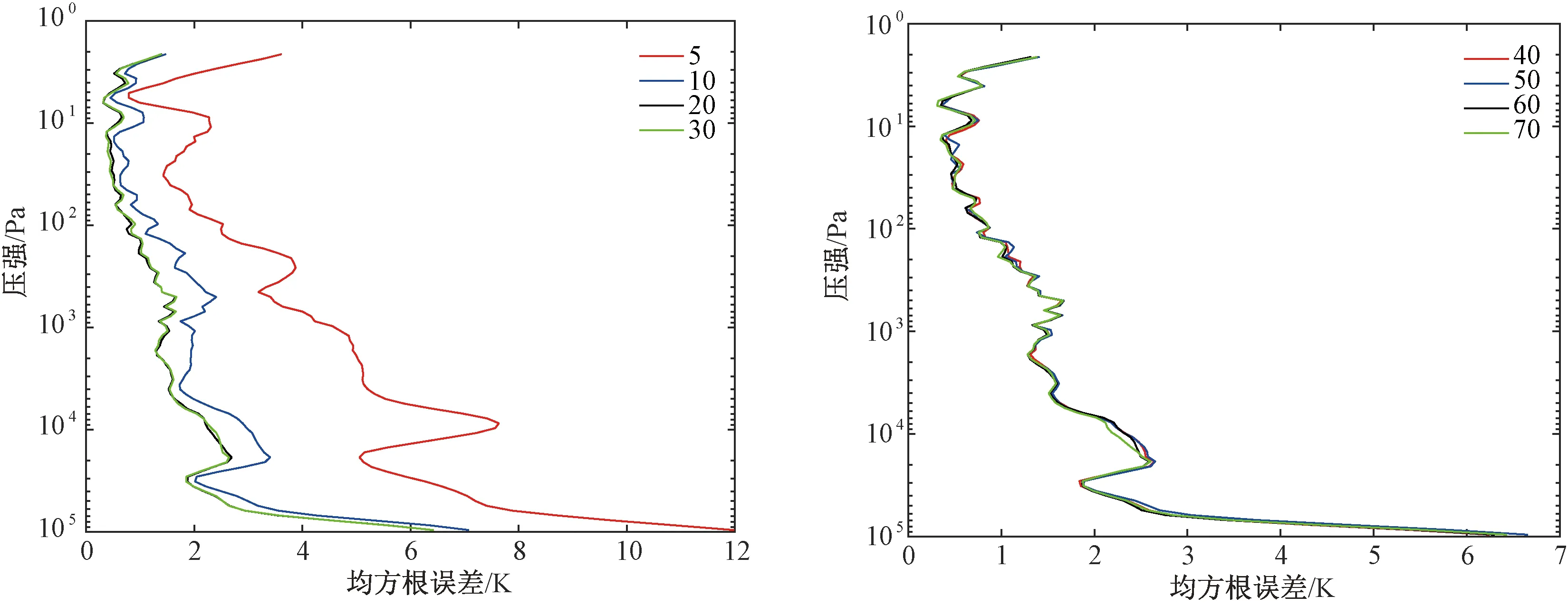
图6 取不同主成分数量的反演均方根误差

由主成分分析实验可以得出结论:在选择主成分的数目较少时,增加其数目可以明显增加反演结果的精度;之后随着主成分的数目逐渐增加,反演精度的提高幅度变得平缓;在达到一定数目后,继续增加主成分数目对反演精度的提高几乎可以忽略。但整体的反演时间和数据量也会随着主成分数目的增加而成比例地增加,特别是神经网络中训练网络的时间增加。所以综合考虑主成分数目对反演精度、反演系统整体效率和数据量等各方面的影响,主成分数目最好取在20～30之间。

2.2 通道选择实验

使用1.2节介绍的通道选择方法从原始数据中选择出100个通道,并进行反演实验。由图4可以看出,在相邻的6～8个选中通道中的权重函数其峰值所在位置随着被选中的顺序不断交替变化。所以以7为基数,分别对选择出的前7、14、21、28、35、49、77、100个通道进行反演实验,实验结果如图7所示。

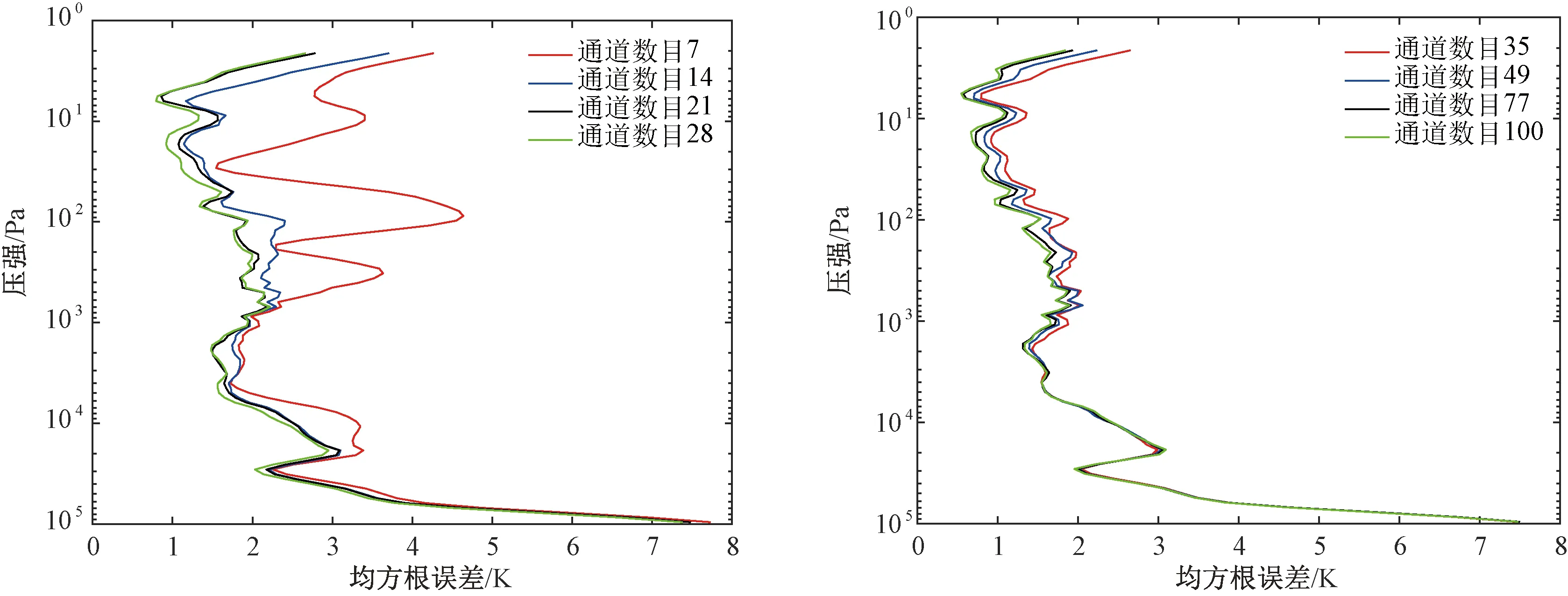
图7 取不同通道数目的反演均方根误差

由图7可以看出,随着通道数的增加,反演精度也在不断增加,且主要体现在中高层大气上,通道数达到一定数量时,继续增加通道数对反演精度几乎没有提高。

2.3 预处理方法对比

用主成分分析法处理高光谱数据后取25个主成分数目,通道选择处理高光谱数据后取77个通道,将这2种不同的预处理数据分别使用神经网络方法对大气温度廓线进行反演,反演结果如图8所示。

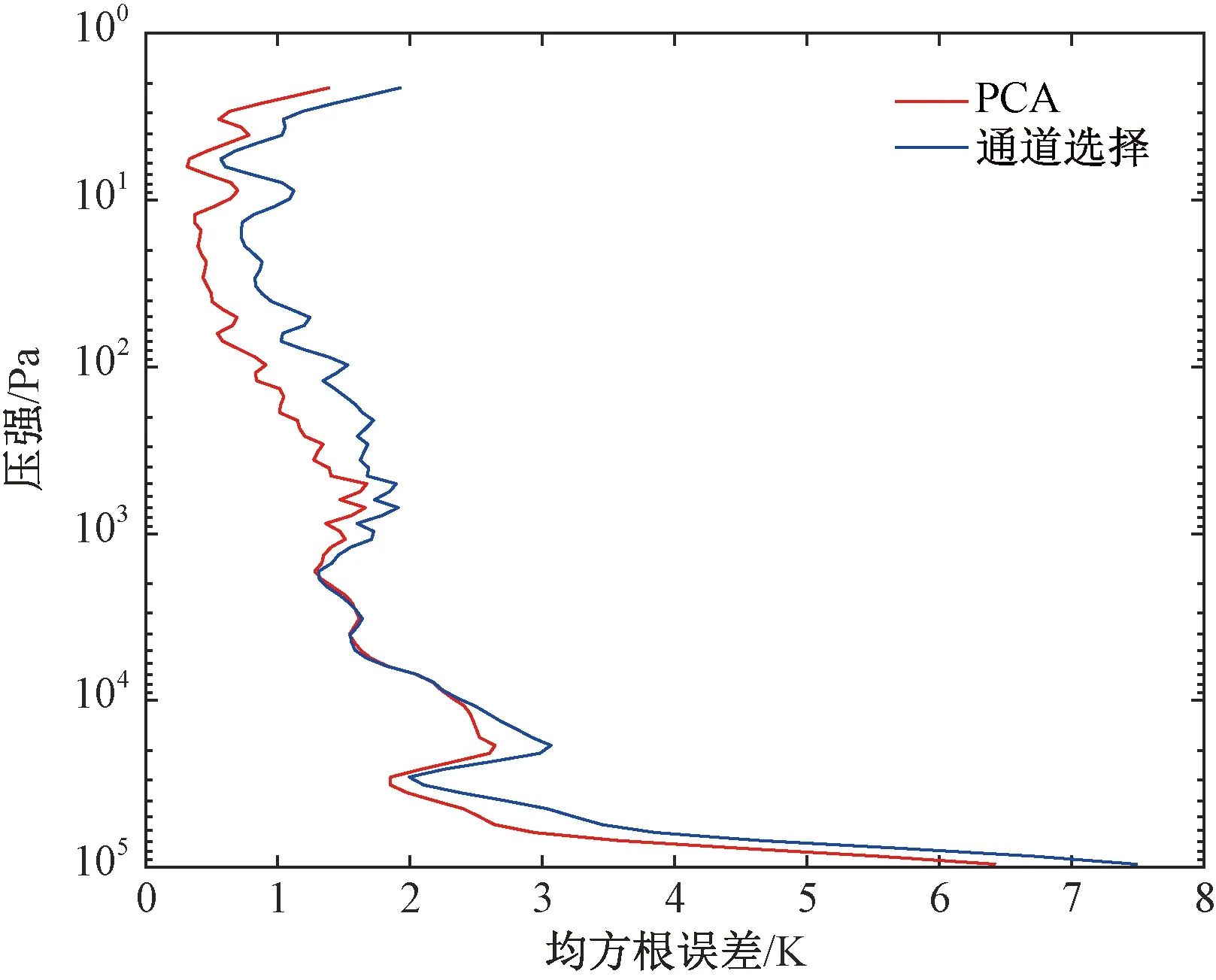
图8 使用不同预处理方法反演结果对比

3 结束语

由图6和图7可以看出,对频率范围为50～60 GHz、通道个数为2 000的高光谱数据来说,主成分分析法的处理结果表明,主成分数目最好取20～30,通道选择法的处理结果分析表明,最佳的通道选择数目应该取在77附近。

从图8可以看出,主成分分析(PCA)预处理方法的反演效果要比通道选择预处理方法的反演效果好。这是因为对主成分分析法而言,取25个主成分时其可以表示原始数据超过99.99%的有效信息,而对于通道选择后的77个通道其代表的有效信息不可能达到这么大,所以才会产生使用PCA预处理的数据反演结果要全面优于通道选择方法的预处理结果。因此,在使用统计反演法和神经网络反演法这些可以直接使用PCA预处理后的高光谱数据的方法来反演大气廓线时,最好使用PCA方法来预处理高光谱数据。

在使用物理反演法时,由于要进行大量的迭代计算,使用PCA会增加计算复杂度并影响反演精度,所以通常使用通道选择来大幅减小计算量。同时经过通道选择后的通道组合可以认为是在此频段中较好的观测通道,对今后微波辐射计在该频段的通道设计具有一定的参考意义。