基于多维傅里叶变换的阵列空时信号处理与应用

石 荣,胡 柱,谢佳霖

(1.电子信息控制重点实验室,四川 成都 610036;2.电磁空间安全全国重点实验室,四川 成都 610036)

0 引 言

传统的相控阵天线工作过程中首先进行空域处理,即通过各个单元天线所接收信号的加权求和形成指向目标信号方向的主波束,以此合成一路信号,然后再对该路信号进行后续的时域处理[1-2]。近年来随着技术的发展,对阵列天线接收的信号进行空时联合处理在工程上的应用越来越广泛[3-4],在此情况下,其数据通常以矩阵形式来表达,以一维线阵产生的二维空时采样数据为例,矩阵的列数与阵列中接收天线单元的个数一致,矩阵的行数与观察时段内每个接收通道的时域采样点个数一致。这意味着每一列数据对应了一个天线单元所接收到的信号,每一行数据对应了同一个采样时刻对所有单元天线接收信号的采样结果,所以该二维矩阵的2个维度分别对应了时间与空间。截止目前,所发展的大量空时联合处理算法都以二维采样矩阵为基础,通过各种运算来完成时空域目标信号的检测、来波方向估计与滤波等功能[5-8]。在工程实现中,对于大中型阵列来讲,由于空时联合处理所涉及的采样信号通常为二维甚至三维矩阵数据,矩阵维数较大,巨大的计算量使其难以在实时性工程任务中应用。

针对上述问题,本文将图像处理中的多维傅里叶变换方法引入到空时信号处理问题中,构建了阵列空时信号处理的工程实现新框架。图像处理中的灰度图像数据是二维矩阵形式,多光谱图像数据是由不同光谱接收传感器形成的高维矩阵形式,而多维傅里叶变换是图像数据进行频谱分析、频率分量增强与滤波的常用处理手段。借鉴图像处理领域的分析方法,将阵列天线接收的信号采样数据看成是一幅图像,一维线阵输出类似于二维图像的数据,二维面阵输出类似于三维图像的数据,通过多维傅里叶变换对上述空时采样数据进行处理,同样能够提取出信号的时频特征与来波方向等信息。所以本文在对信号时域与空域对偶关系概要总结之后,将傅里叶变换从时域推广至空域,指出了空域与角度域之间存在的傅里叶变换关系,然后分别对线阵与面阵的空时联合处理的二维与三维傅里叶变换的表达及其物理意义进行了详细的阐述,并通过示例性仿真验证了前述理论分析的正确性与有效性。

1 将傅里叶变换从时域推广至空域

通过傅里叶变换将时域信号变换至频域而得到信号的频谱,对此大家早已熟悉。但是对空域采样信号实施傅里叶变换,并清晰地解释其物理意义,这还需要从时域与空域之间的对偶关系谈起。

1.1 时域采样定理与空域采样定理

对一个连续时间信号x(t)进行时域离散采样,当采样频率大于信号最高频率的2倍时,采样之后的离散信号完整地保留了原始信号中的所有信息。从理论上讲,通过采样信号能够完整地恢复原始信号x(t),这就是大家十分熟悉的时域采样定理,又称为奈奎斯特采样定理。

实际上在空域中也有相应的采样定理,即对空间中传播的信号x(t,d)在某一时刻t0的空间样本x(t0,d)进行采样,只有当空间上的采样间隔小于信号波长的一半,即λ/2时,采样之后的空间信号才能完整地保留原始信号x(t0,d)中与空间传播方向相关的所有信息。换句话讲,空域采样定理要求在1个信号波长的空间距离上至少要有2个采样点。如果将单位长度上的波数1/λ看成是一种空间频率,那么空域采样定理同样要求空间采样频率大于信号空间频率的2倍。

由上可见,信号的时域采样定理与空域采样定理具有对偶性,这也为将时域信号处理方法推广应用于空域提供了条件。

1.2 时域与频域之间的傅里叶变换关系

对一个信号进行时域处理一般要求信号带宽与伴随的噪声带宽基本一致,这样才能获得较好的效果,所以通常采用与信号带宽基本相同的滤波器对采样信号进行滤波,滤除带外噪声与其他干扰之后就能满足这一条件。于是将信号由时域变换至频域,通过频谱分析得到信号的带宽等参数。具体来讲,在给定的观察时段内,时域采样信号x(n),n=0,1,…,N-1,与其频域频谱X(k1)(k1=0,1,…,N-1)之间满足如下傅里叶变换关系:

(1)

在工程上,式(1)通常由快速傅里叶变换来实现,这也是信号分析处理工程应用中最常见的手段。如果将傅里叶变换应用于空域,其变换结果所展现的物理意义,下面以一维线阵为例进行分析。

1.3 空域与角度域之间的傅里叶变换关系

空间中一维均匀线阵包含N个单元天线,记单个信号入射到阵列上时所输出的信号为ys(n,m):

ys(n,m)=yt(nTs-2πmdscosθs/λ,0)

(2)

式中:第1个变量n表示时域采样序号,n=0,1,…,N-1,N为时域中总的采样点数;第2个变量m表示空域采样序号,m=0,1,…,M-1,M为线阵中单元天线的个数;yt(t,0)=xt(t),表示第0号单元天线接收到的连续时间域的信号;Ts表示时间采样间隔;ds表示空间采样间隔,即相邻2个单元天线之间的距离;λ为信号波长;θs表示信号来波方向与线阵基线之间的夹角,且θs∈[0,π]。

在实际工程应用中的大多数情况下,信号带宽远小于信号载频,满足窄带接收条件,于是式(2)可简化为:

ys(n,m)≈xt(nTs)·exp(-j2πmdscosθs/λ)

(3)

如果对某一时域采样时刻ns0的M个单元天线采集的信号ys(ns0,m)进行空域傅里叶变换,其结果记为Y(ns0,k2),k2=0,1,…,M-1,于是可得:

(4)

参照时域傅里叶逆变换表达方式,得到与式(4)相关的空域傅里叶逆变换:

(5)

空域傅里叶变换与逆变换中变量k2的物理意义主要体现在信号来波方向的角度信息上,所以空域与角度域是1对傅里叶变换关系式。

时域信号通过傅里叶变换变换至频域,得到信号的频谱;将空域信号通过傅里叶变换变换至角度域,可以得到信号的角度谱。信号频谱反映了信号所包含的不同频率分量的分布与构成情况;而信号的角度谱则反映了信号入射到一维线阵上的来波方向角度的特征信息。将式(3)代入式(4)可得:

Y(ns0,k2)=xt(ns0Ts)·

(6)

式(6)实际上描述了变量k2与信号来波方向角θs之间的对应关系,由于k2取值[0,M-1]范围内的整数,而来波方向角θs的取值范围为[0,π]。所以,在对上述空域傅里叶变换后所得到的角度谱的物理意义解释,需要特别注意坐标单位的平移对应关系。

(1)当θs∈[π/2,π]时,有:

(7)

由式(6)可知:在k2对应的角度θs方向上相干汇聚了整个一维均匀线阵M个单元天线接收的来波信号,并且会在角度θs上出现一个峰值。当k2从0变化到M/2时,由式(7)可解得:

θs=arccos(-k2λ/(Mds))

(8)

由式(8)可知,当ds=λ/2时,k2从0变化到M/2对应了θs从π/2变化到π。

(2)当θs∈[0,π/2]时,有:

(9)

同样由式(6)可知,在k2所对应的角度θs方向上相干汇聚了整个一维均匀线阵M个单元天线接收的来波信号,并且会在角度θs上出现1个峰值。于是当k2从M/2变化到M-1时,由式(9)可得:

θs=arccos((M-k2)λ/(Mds))

(10)

由式(10)可知,k2从M/2变化到M-1对应了θs从0变化到接近π/2。

由于离散傅里叶变换具有周期性,如果以k2=0时对应的来波方向角θs=π/2为中心,按照周期性,k2从M/2变化到M-1等效对应了k2从-M/2变化到接近于0,于是来波方向角θs从0变化到π就与k2从-M/2变化到M/2完全对应起来了。

在以上空域与角度域的变换关系分析过程中采用的是单个信号,如果有多个信号从不同角度方向同时入射到一维线阵上,针对每一个信号而言,式(2)均成立,在窄带信号应用条件下,阵列中所有单元天线输出的信号y(n,m)可表示为:

(11)

式中:Ls表示同时入射到阵列中的信号个数;θs,i表示第i个信号的来波方向线与阵列基线之间的夹角。

将式(11)代入式(4),可得某一时域采样时刻ns0的M个单元天线采集的信号y(ns0,m)的傅里叶变换结果Y(ns0,k2)。时域信号的傅里叶变换满足线性叠加原理,空域信号的傅里叶变换同样满足线性叠加原理,所以式(4)与式(5)所表示的空域与角度域之间的傅里叶变换与逆变换表达式对同时入射到阵列上的多个信号仍然成立。

2 线阵空时联合处理的二维傅里叶变换表达及物理意义

在给定的观察时段内,一维线阵采样得到的空时数据的二维矩阵,其元素记为y(n,m),其中自变量n与m分别代表时域与空域采样序号,矩阵大小为N×M。对y(n,m)进行二维傅里叶变换的结果记为Y2(k1,k2):

Y2(k1,k2)=

(12)

如前所述,Y2(k1,k2)展示了时域与空域相对应的频域与角度域的信号分量分布情况,其中第1个自变量k1代表频域分量序号,反映了信号频率分量的分布,第2个自变量k2代表角度域分量序号,反映了不同信号的一维来波方向,如图1所示。

图1 线阵数据的二维傅里叶变换中各物理量的转换关系

在计算实施方面,将式(12)改写成如下形式:

(13)

由式(13)可知,空时采样数据矩阵的二维傅里叶变换能够通过(N+M)次一维傅里叶变换来实现,前N次一维傅里叶变换是针对y(n,m)的M列数据进行,分别将各个单元天线接收的时域数据变换至频域,从而得到1个相同维度的中间形式的二维矩阵,其元素记为Yy(k1,m),然后再对Yy(k1,m)的N行数据进行N次一维傅里叶变换,从而最终得到Y2(k1,k2)。而上述N+M次一维傅里叶变换均能够通过快速傅里叶变换来实现,所以在工程应用中线阵信号的二维傅里叶变换的计算量并不大。特别是对于大中型阵列天线来讲,本方法相对于传统的基于信号互相关矩阵分解的空间谱之类的方法,计算量更小,并具有可实时计算的优势。

在物理意义上,变换结果的模值平方‖Y2(k1,k2)‖2完整地反映了不同频率信号从不同角度到达一维线阵的能量分布情况。通过‖Y2(k1,k2)‖2不仅可实现信号的频域检测、频率与带宽参数的估计,而且还能估计各个信号的来波方向角度参数。

式(12)和式(13)的运算对信号并没有附加特定的限制条件,即便是频率相同的多个信号同时入射到一维线阵中时,只要这些信号的来波方向不同,在线阵阵元个数足够多的情况下,也能够将各个同频信号的来波方向信息逐一提取出来。这一点是线阵空时联合处理中二维傅里叶变换相对于传统的基于阵列信号互相关矩阵分解的MUSIC类空间谱估计算法的优势所在。在MUSIC等算法中,为了避免同频多信号所引入的互相关矩阵的秩亏损等问题,需要采用子阵平滑等操作,不仅计算繁杂,而且性能还会下降;而本方法直接通过快速傅里叶变换即可分辨同时到达的多个同频信号。

3 面阵空时联合处理的三维傅里叶变换表达及物理意义

在工程应用中,阵列形式有线阵和面阵,面阵相对于线阵增加了一个空间维度,其空时采样数据由二维矩阵变成了三维矩阵,包含1个时间维度和2个空间维度,可记为y(n,m,l),其中第1个自变量n代表时域采样序号,第2个自变量m代表横向空域采样序号,第3个自变量l代表纵向空域采样序号,整个矩阵大小为N×M×L。对y(n,m,l)进行三维傅里叶变换的结果记为Y3(k1,k2,k3):

Y3(k1,k2,k3)=

(14)

式中:k1代表频域分量序号,反映了信号频率分量的分布;k2与k3分别代表了二维角度域分量序号,反映了不同信号的二维来波方向,如图2所示。

图2 面阵数据的三维傅里叶变换中各物理量的转换关系

作为前一节相关理论分析结果的推广,对面阵空时采样数据进行三维傅里叶变换同样可以通过(NL+LM+MN)次一维快速傅里叶变换来实现,在工程上可实时实现。2个空间维度变换之后也对应了2个角度维度的数据,从物理意义上讲,分别表示了各个信号来波方向与面阵相互垂直的2条基线之间的夹角。二维平面上的信号来波方向用1个角度参数即可描述,而三维空间中的信号来波方向需要用2个角度参数来描述,例如工程上常常用来波方向的方位角与俯仰角来描述,在此所使用的2个角度参数分别是来波方向与面阵2条正交测量基线之间的夹角,由立体几何可知该夹角与方位角、俯仰角之间可以相互换算。于是三维傅里叶变换结果的模值平方‖Y3(k1,k2,k3)‖2同样完整地反映了不同频率的信号从三维空间不同角度到达二维面阵的能量分布情况。通过‖Y3(k1,k2,k3)‖2同样能够实现信号的频域检测、频率与带宽参数的估计、对各个信号的来波方向角度参数的估计。而且对于同频多信号同时达到二维面阵的情况在阵元个数足够多的情况下也可进行分辨。

4 仿真与应用示例

(1)一维均匀线阵采样信号的二维傅里叶变换

由128个单元天线构成的一维均匀线阵中,相邻单元天线的间距为0.12 m,有3个相等功率的1.25 GHz的同频信号分别从不同的方向入射,第1个为脉宽0.5 μs的单频雷达脉冲信号,第2、3个为连续波瞄频干扰信号,上述3个信号的来波方向线与线阵基线之间的夹角分别为57°,106°,113°。以3 GHz采样频率在信号持续存在期间进行连续采样0.2 μs,从而得到一个600×128的二维采样信号矩阵。

按照前述的线阵空时联合处理的二维傅里叶变换方法,首先进行128次列方向上的一维时域傅里叶变换,然后对变换后的数据再进行600次行方向上的一维空域傅里叶变换,从而将时域与空域的采样信号矩阵变换成了频域与角度域的二维矩阵,各元素求模之后如图3所示。

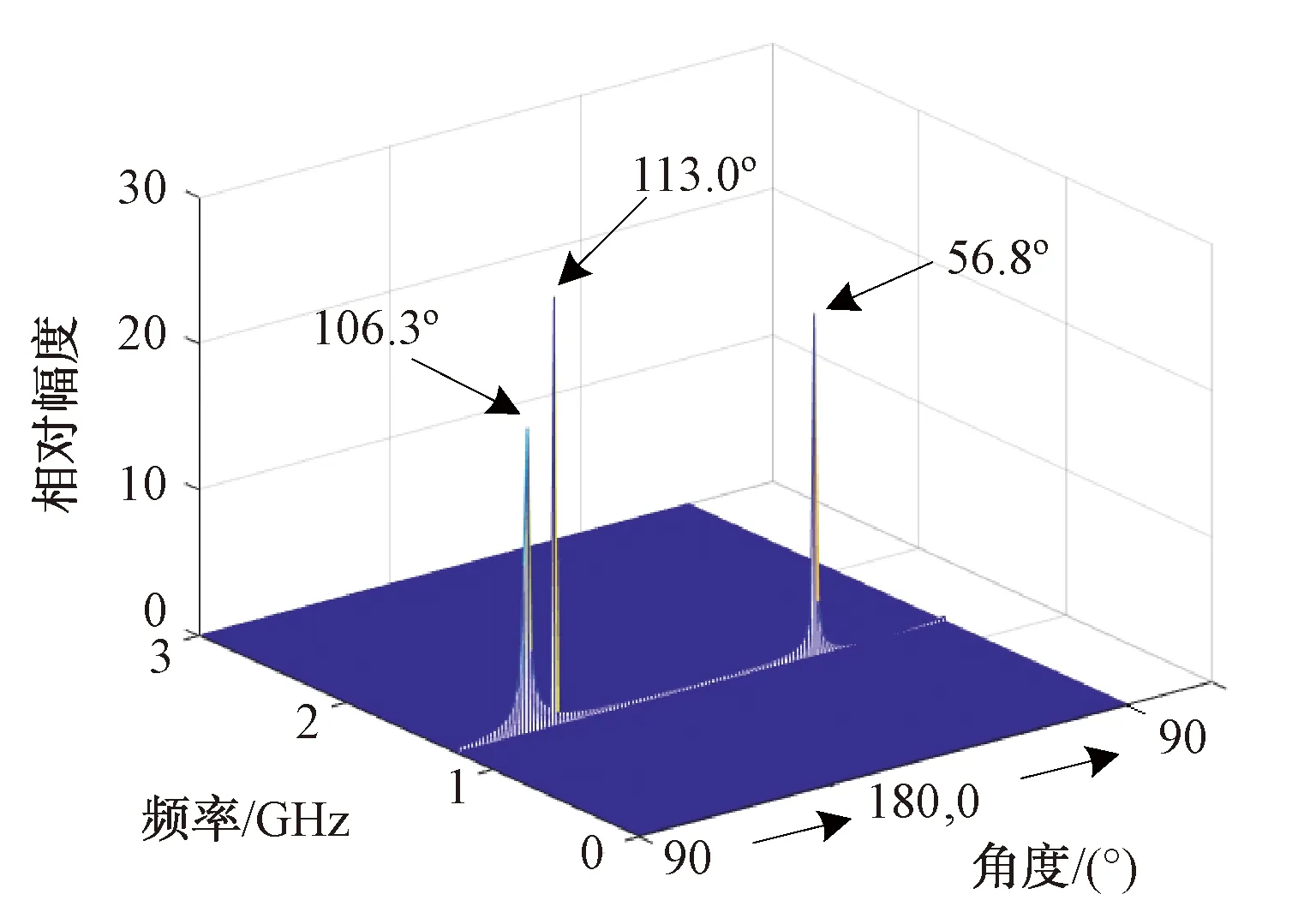
图3 二维傅里叶变换后展示的频域与角度域结果

图3中的3个峰值分别对应了3个信号,在频率维度3个信号的频率相同,均为1.25 GHz,在角度维度3个信号的来波方向分别为56.8°,106.3°,113.0°。由此可见,从一维线阵采样的空时信号的二维傅里叶变换中不仅可以获得各个信号的频率,而且还能对同频多信号的不同来波方向进行估计。

(2)二维均匀面阵采样信号的三维傅里叶变换

将前述一维线阵扩展成128×128的二维均匀面阵,相邻单元天线的间距仍然为0.12 m,同样是前述3个信号入射,入射角度与面阵的2条正交基线的夹角分别是:(57°,120°),(106°,45°),(113°,98°)。同样以3 GHz采样频率在信号持续存在期间进行连续采样0.2 μs,从而得到一个600×128×128的三维采样信号矩阵。

按照前述的面阵空时联合处理的三维傅里叶变换方法,首先进行128×128次列方向上的一维时域傅里叶变换,然后对变换后的数据再进行600次二维空域傅里叶变换,从而将时域与空域的采样信号矩阵变换成了频域与角度域的三维矩阵。每一次二维空域傅里叶变换还可以继续分解成256个一维傅里叶变换,所以总的计算量并不大。由于三维矩阵难以在平面上展示,所以用切分方式进行局部观察,以频域频率采样序号等于250的频点对三维矩阵进行切片,该切片对应的信号频率为1.25 GHz,从而得到一个128×128的二维矩阵,该矩阵的2个维度分别是来波方向线与2条正交基线之间的夹角,该二维矩阵的各元素求模之后如图4所示。

图4中的3个峰值分别对应了3个信号,在频率维度3个信号的频率相同,均为1.25 GHz,在角度维度3个信号的二维来波方向分别为(56.8°,120.0°),(106.3°,45.3°),(113.0°,98.1°)。由此可见,从二维面阵采样的空时信号的三维傅里叶变换中不仅可以估计出各个信号的频率,而且还能对同频多信号的不同来波方向进行准确估计。

5 结束语

在大中型阵列天线所接收信号的空时信号处理过程中,由于阵元数量众多,导致空时采样数据矩阵的维数很大,高维矩阵运算所需巨大计算量给实时处理类的工程应用带来了极大的困难。本文借鉴图像处理中的多维傅里叶变换方法,将时空域采样数据进行多维傅里叶变换,而这些变换均能够分解并利用更低维数的快速傅里叶变换来实现,从而为工程上的实时处理创造了条件。而且空域与角度域的傅里叶变换关系也使得该方法将大中型阵列的空时数据转换成了频域与角度域的数据,实现了信号的频域参数提取与来波方向估计。最后通过仿真验证了理论分析的正确性,同时也展现了线阵与面阵各自空时联合处理的二维与三维傅里叶变换的本质物理意义,从而为大中型阵列的空时信号实时处理工程应用提供了新的技术手段。