基于随动时变风载荷的车载导弹发射动力学研究

缴天航，姜 毅，王 登，严 松

(北京理工大学宇航学院，北京 100081)

0 引言

随着现代武器对目标精确打击精度的提高,传统导弹武器的作战能力受到了严重威胁,未来新型战争对导弹系统的生存能力提出了更高的要求。与传统发射方式相比,车载导弹武器系统具有高机动性的特点,在提高系统自身的生存能力的同时也导致了系统在发射过程中稳定性与精度的下降。风载荷是车载导弹发射过程中一项重要的外界激励因素,尤其对于垂直发射的导弹而言,风载荷的影响更加不可忽视。风载荷的作用具有随机不确定性,因此会对导弹系统的稳定性和发射精度造成影响。

国内外学者针对风载荷作用下导弹发射动力学作了大量工作,刘瑞卿等[1-2]根据风载荷的相关特性,分别对平均风剖面与指数风剖面进行了推导,建立了导弹-发射车流场域动网格模型与多刚体动力学模型,基于单向流固耦合理论,使用FLUENT和ADAMS进行联合仿真,分别研究了平均风和脉动风对垂直冷发射导弹在待发状态与发射过程中的影响,推导了导弹-发射车稳定性的安全系数公式,对地面风载荷作用下弹-车系统起竖后的稳定性进行了研究。李显龙等[3]将风载荷简化为力与力矩,研究其对舰载导弹出筒的水平位移、弹射高度与姿态角的影响。高宇等[4]将风载荷简化为若干组依次生效的水平力,对井基导弹冷发射出筒的导弹的偏移、偏航与适配器受力进行研究。黄韬[5]分别采用全动力计算方法与等效静力载荷法对顺风向载荷进行了计算,分别使用两种风载荷对某型发射装备进行动力学分析,得到风载荷作用下发射装备的动态响应,对比分析风载对装备待发状态下的影响。

然而,通过文献调研发现一些问题,主要集中在两方面。一方面,发射系统模型被简化为全刚体动力学模型,该简化方法无法反映发射系统的振动特性与变形。另一方面,风载荷的加载方式是将载荷直接加载于质心或分段依次加载,这两种风载荷的加载方法均不能真实地模拟导弹出筒过程中具有随动时变特性的风载荷。

针对上述问题,并考虑到导弹在出筒过程中弹体表面风载作用区域不断增大,该过程具有随动特性与时变特性,文中建立了车载导弹发射系统有限元模型,并运用ABAQUS用户子程序进行联合二次开发,实现了随动风载荷的实时加载,该方法在导弹发射动力学仿真与应用中鲜有报道。基于该模型和方法,研究了风载荷作用下,风速、推力偏心和地面倾角对导弹姿态和发射筒振动的影响。该研究成果可为车载导弹武器系统的设计提供参考,并为其他领域随动时变载荷的研究提供新思路。

1 风载荷原理

地面风一般是指从地面到150 m高度这一范围内的大气流动[1]。而风载荷是指当导弹在发射车上进行起竖过程或处于待发射状态时,或导弹处于发射过程中与导弹刚出筒时的无控段,地面风对导弹及发射车产生的定常与非定常载荷。这种载荷会使发射装置结构产生振动与应力变形,影响导弹的初始弹道与发射装置校正精度;严重时可能会导致发射装置的破坏或侧倾,并造成发射人员的伤亡和发射装置的损毁。

在实际研究中,一般可以认为风平行于地面,同时为了便于研究,将风载荷分解为垂直射击平面的分量(横风)与平行射击平面的分量(纵风)。

瞬时风模型包括长周期与短周期两个部分,因此可以根据风载荷的周期长短将风分为平均风和脉动风[6]。平均风的周期较长,通常可以达到10 min以上,相比于导弹的自振周期更长,因此这部分风载荷产生的是静载荷;而脉动风的周期与导弹系统的自振周期较为相近,其作用效果为动载。

通常用风速或者风压两种方式表示风载荷的大小,文中以风速为例。根据相关实验资料[7]可得出一个结论:在一定高度的风速总会在其平均值附近变化。任一位置处的水平风速可以表达为:

u(h,t)=u0(h)+Δu(h,t)

(1)

式中:u(h,t)表示在高度h处t时刻的风速;u0(h)表示平均风速;Δu(h,t)表示随机脉动部分,即瞬时风速相对于平均风速的变化量。

对于平均风,认为它的作用效果为静力的,可以将其直接简化为恒定值;对于脉动风,由于发射出筒时间一般在1～2 s以内,时间较短,因此低频脉动风在这段时间变化较小,在工程中可将其简化为恒定载荷。综上所述,风作用于导弹上的载荷均被简化为静载荷,通过空气阻力法进行计算,其值的大小由多个因素决定,包括导弹弹体的迎风面积,导弹本身的气动阻力系数和当地的风速(或风压)。具体公式为[7]:

F=qiSi

(2)

式中:F为导弹所受风载荷;Si为导弹的计算迎风面积;qi为与计算面积相对应的计算风压。计算风压是指考虑风的性质、导弹自身结构与导弹高度后的风压为[7]:

qi=qCxRhβ

(3)

式中:q为额定风压;Cx为导弹的气动阻力系数,它取决于导弹的迎风外形,根据结构进行选取。对于圆柱形结构,当qd2≤9.8 N时,Cx=1.2;当qd2≥14.7 N时,Cx=0.7;当qd2介于其间,则利用内部插值来决定。由于文中将导弹简化为圆柱体与圆锥体的组合,主体为圆柱体,且所取工况风速较大,故该值取为0.7。Rh为风压随着高度而增加的系数,取为1.0;β为考虑阵风作用下的修正系数,取为1.22。

式(3)中,q为额定风压,即风以某恒定风速稳定作用的压力,其值可表示为[7]:

(4)

式中:ρ为空气密度,它与当地气温有关,取15℃下的空气密度1.226 kg/m3;v为风速,由两地之间的气压差决定,气压差越大,风速越大。

2 动力学模型建模

通过有限元分析仿真软件ABAQUS建立车载导弹武器系统的动力学模型,模型主要由车架、发射筒、车头、车身、轮胎、支腿、起竖油缸、适配器和导弹等部分组成,如图1所示。模型说明如下:

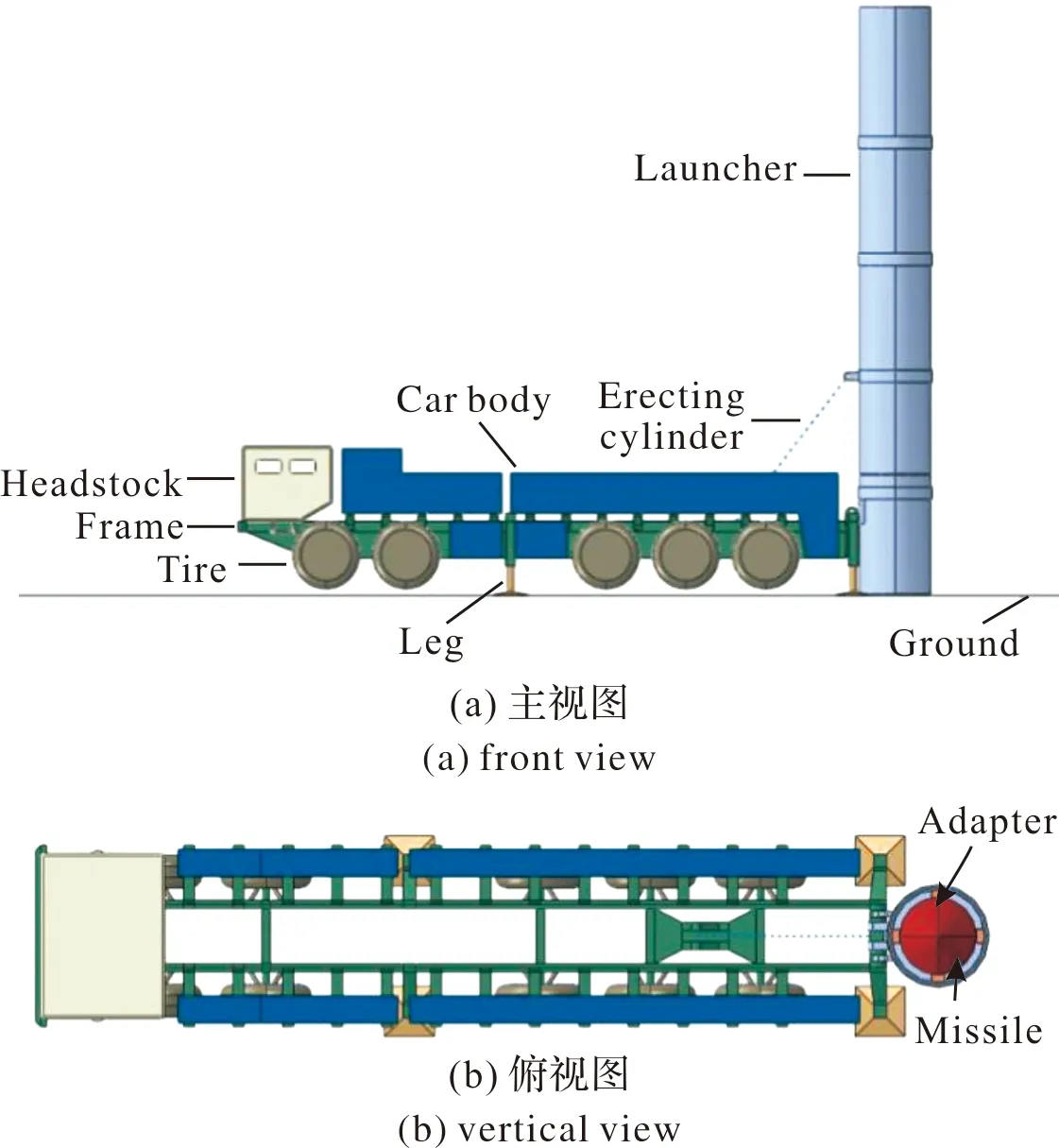
图1 车载导弹发射系统模型示意图Fig.1 Schematic diagram of vehicle mounted missile launch system model

1)X轴方向为车头指向车尾方向,Y轴正向为导弹发射方向,Z轴正方向由右手定则确定。

2)车架、支腿与发射筒均采用实体六面体单元C3D8R进行建模,其中发射筒筒壁厚0.04 m,筒壁外设置四组加强筋,支腿高1.8 m,车架全长15.5 m。

3)导弹使用壳单元S4R进行建模并为其附加厚度,同时在弹体质心位置设置质量点,全弹总质量为36 090 kg,弹长11.5 m。

4)适配器使用实体六面体单元C3D8R进行建模,其中适配器共有4组,每组适配器有4个,共计16个适配器,适配器的布局与网格划分如图2所示。

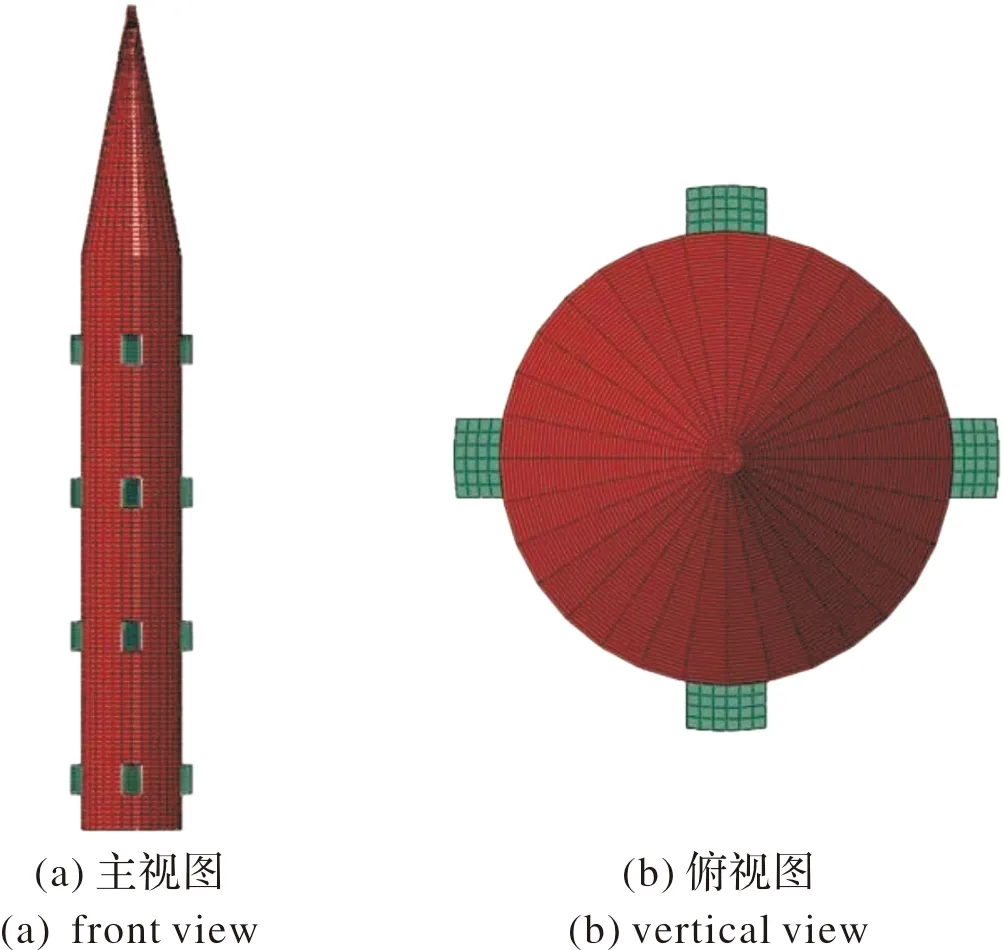
图2 适配器布局与网格划分示意图Fig.2 Schematic diagram of adapter layout and grid division

5)起竖油缸利用刚性弹簧进行模拟,分别在起竖油缸的上下支撑点建立参考点并与对应面进行耦合,两参考点之间采用滑移连接,根据工程经验弹簧刚度取为1.6×108N/m。

6)在发射筒左右筒筋圆孔中心建立参考点,参考点与圆孔耦合;在车架尾端回转轴中心建立参考点,参考点与回转轴圆孔面耦合。两个参考点之间通过铰接连接模拟旋转副。起竖油缸上支点与发射筒、起竖油缸下支点与车架之间也通过此方式建立铰接连接。部分柔性体之间连接关系以及网格划分如图3所示。

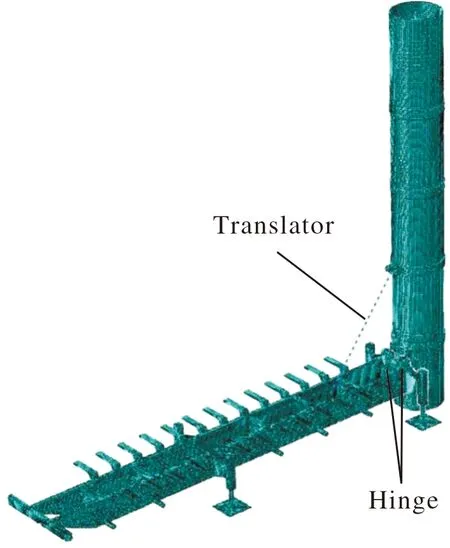
图3 部分柔性体之间连接关系以及网格划分示意图Fig.3 Schematic diagram of the connection relation between some flexible bodies and grid division

7)忽略地面的柔性影响,采用刚体进行模拟;车头、车身、轮胎在发射时均只作为配重与车架相连,因此均设置为刚体。刚体均采用离散刚体,在部件质心创建参考点以设置质量点。其中车头、车身、轮胎与车架的总质量为52 010 kg。

8)上述部分柔性部件材料参数如表1所示。

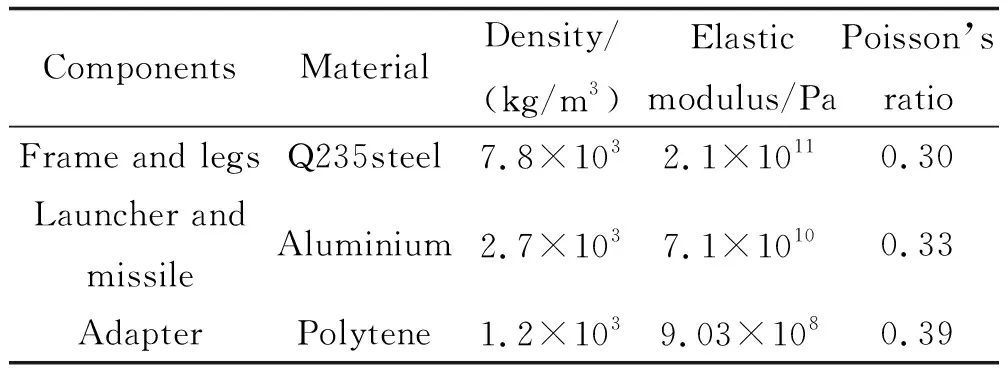
表1 模型材料参数表Table 1 Parameters of model materials

对于仿真模型的载荷设置如下:

1)由式(2)～式(4)可以计算出导弹表面单位迎风面积所受风载荷qi。其中风载荷对导弹的作用过程如图4所示。当导弹发射前,弹体全部位于发射筒内,因此导弹不受风载荷影响;当导弹处于发射出筒过程时,部分弹体位于发射筒外,此时位于筒外的这部分弹体表面开始受到风载荷作用,且随着导弹不断出筒,风载荷的作用面积不断扩大;当导弹完全出筒后,整个弹体均受到风载荷的作用。上述发射过程中,弹体实时位置控制着风载荷实时作用区域,具有随动特性;弹体表面风载荷作用区域与风载荷幅值大小随着导弹的实时位置变化而动态变化,具有时变特性。

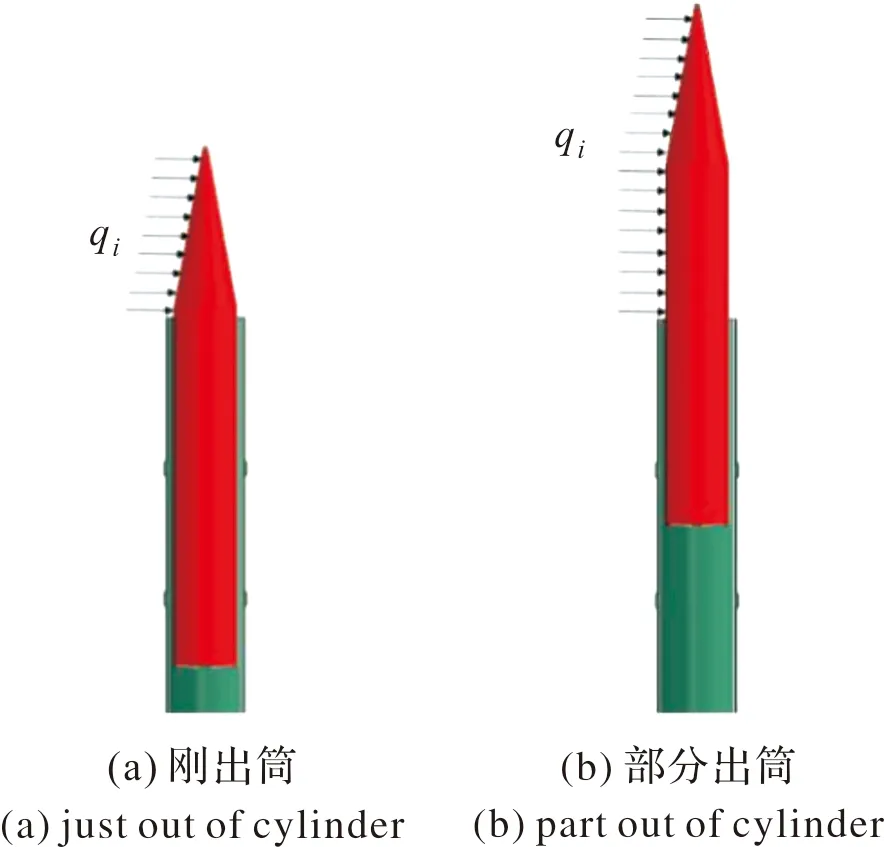
图4 风载荷对导弹出筒作用过程示意图Fig.4 Schematic diagram of the process of wind load on missile ejection

可借助ABAQUS用户自定义子程序(Dload或Utracload子程序)实现上述随动时变过程:主程序中设置单位面积所受风载荷大小与风载荷位置,并在每个增量步进行子程序调用,将风载荷作用节点实时坐标等参数实时传入至子程序。用户子程序对选定区域中每个积分点进行重复操作,将积分点x向实时坐标与筒口位置坐标进行比较,若满足位置要求,认为此处已经出筒,则为此积分点进行载荷加载;若不满足,则不进行加载。当所有节点均完成该步骤后,则进入下一增量步,其实现流程示意图如图5所示。

图5 子程序实现风载荷随动时变加载过程示意图Fig.5 Schematic diagram of wind load time-varying loading process realized by subroutine

2)在导弹尾部中心施加如图6所示的推力曲线,模拟导弹发动机产生的推力。

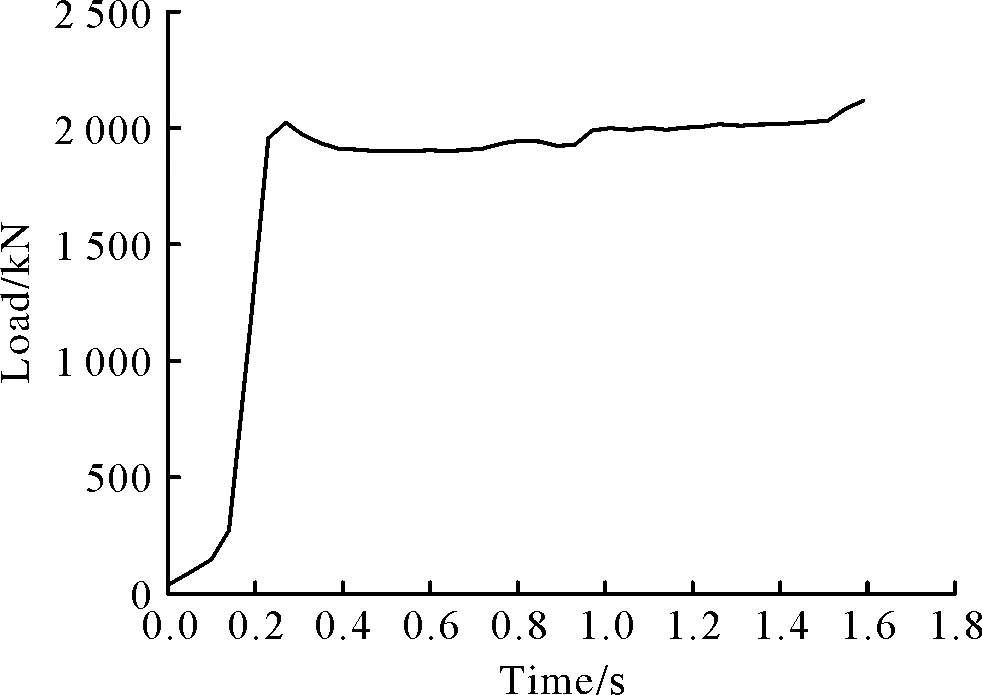
图6 导弹推力曲线图Fig.6 Missile thrust curve

3)对模型整体施加重力场,重力加速度为9.8 m/s2,方向竖直向下。

对于仿真模型的相互作用与边界条件设置如下:

1)为防止发射前导弹沿筒壁下滑,在发射筒内部设置了一个与其固连的挡板。发射筒底部与刚性地面、导弹底部与发射筒挡板之间设置面面接触,切向摩擦系数设为0.2,法向设为硬接触;适配器与发射筒内壁之间添加面面接触,切向摩擦系数设为0.1,法向设为硬接触,接触间隙为0.01 m。

2)在导弹外表面与适配器内侧表面、车架与支腿侧面、支腿下表面与地面上表面之间设立绑定约束。

3)将刚性地面底部进行六自由度完全固定。

在完成上述建模后,将整个仿真过程分为静平衡与发射动力学两个过程。静平衡分析步采用静力通用分析步,分析步时长为1 s,该分析步仅受到重力作用,其目的是为了消除动力学分析步初始时刻重力带来的影响。静平衡分析步结束后,认为发射装置达到静平衡状态,进入发射过程分析步,发射过程分析步采用动力隐式分析步,分析步时长为1.6 s。

3 结果与分析

发射过程示意图如图7所示。其中图(a)为0.18 s时弹尖开始出筒,图(b)为0.67 s第一级适配器出筒,图(c)为0.76 s第二级适配器出筒,图(d)为0.83 s第三级适配器出筒,图(e)为0.9 s第四级适配器出筒,图(f)为0.92 s导弹出筒。

图7 导弹发射过程示意图Fig.7 Schematic diagram of missile launching process

3.1 风速的影响分析

考虑到发射装置的相关结构特性,主要研究风载荷在Oxy平面内的作用效果,风载荷的方向以x轴正向为正,如图8所示。风速是影响导弹姿态的风速方向即为风载荷作用方向,选取风速分别为0 m/s,15 m/s,17.5 m/s,20 m/s,22.5 m/s,25 m/s共6种工况,分析导弹发射过程中姿态变化规律与发射筒振动情况。

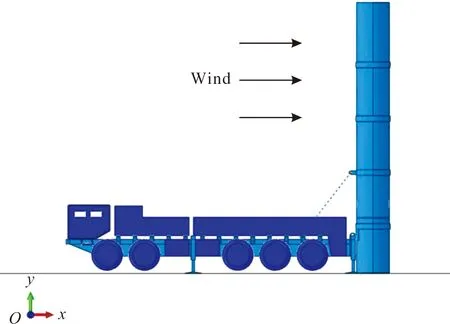
图8 风载荷方向示意图Fig.8 Schematic diagram of the wind load direction

图9为不同风速下导弹头部、质心与尾部在导弹发射过程中x方向位移曲线。

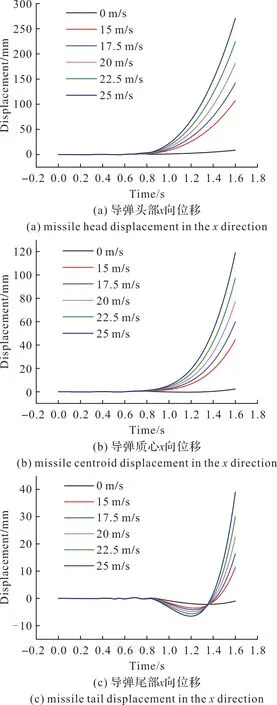
图9 不同风速下导弹头部、质心与尾部x向位移量Fig.9 xdirection displacement of missile head, centroid and tail under different wind speeds

导弹离筒前受到适配器导向作用的限制,位移较小;导弹离筒后受风载荷作用,整体向风速方向(x正向)偏移,随着风速增大位移显著增大。导弹头部先出筒,受风载荷作用时间较长,持续向x正方向偏移,位移较大且持续增大;而尾部位移较小且在出筒时间附近先减小后增大,这是由于风载荷先作用于先出筒的导弹上段从而将其吹偏,而导弹下端未出筒部分受到发射筒约束,以筒口适配器为支点作杠杆运动,导致导弹下端出现小幅度的反向位移,如图10所示。

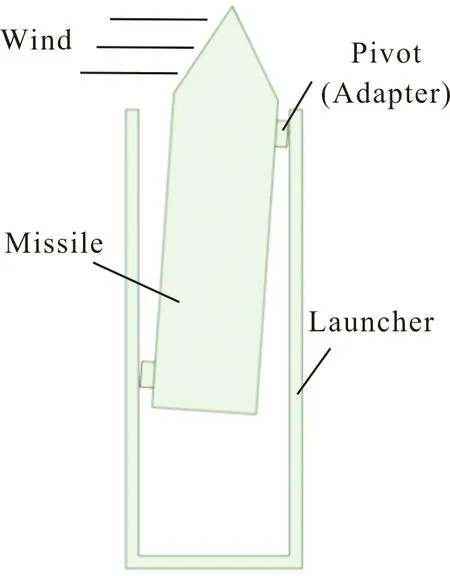
图10 导弹出筒过程杠杆运动示意图Fig.10 Schematic diagram of lever movement during missile ejection

图11为不同风速下导弹发射过程中质心俯仰角位移和俯仰角速度曲线。

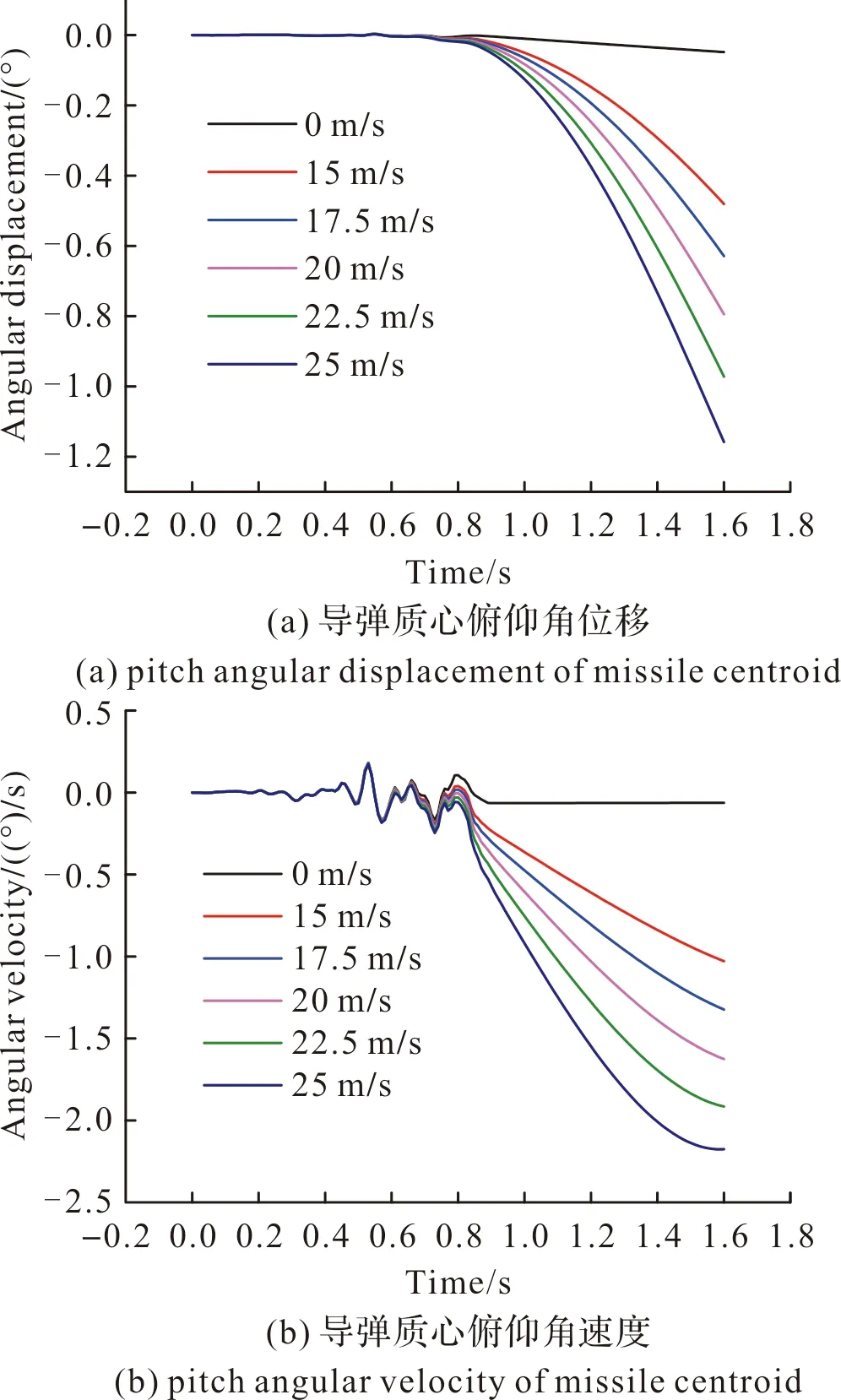
图11 不同风速下导弹质心俯仰角位移与俯仰角速度Fig.11 Pitch angular displacement and pitch angular velocity of missile centroid under different wind speeds

导弹在离筒时刻的俯仰角位移与俯仰角速度如表2所示。导弹离筒前受到适配器导向作用的限制,角位移和角速度较小;导弹出筒后,俯仰角位移和俯仰角速度受风力影响而增大,且随着风速的增大俯仰角位移和俯仰角速度显著增大。

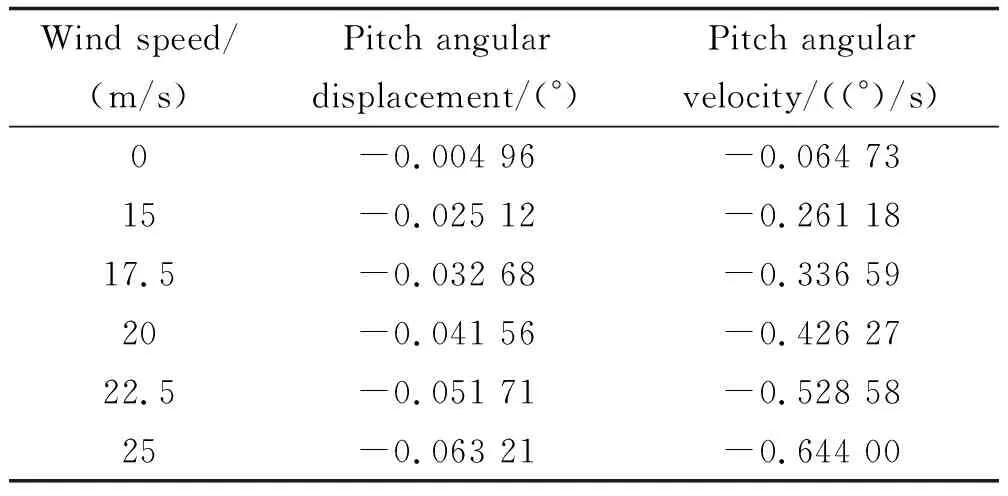
表2 不同风速下离筒时刻俯仰角位移与俯仰角速度Table 2 Pitch angular displacements and pitch angular velocities at the moment of departure from the cylinder under different wind speeds

图12为不同风速下发射筒在导弹发射过程中沿x方向位移曲线。发射筒在发射过程中反复振动,在0.8 s左右振幅最大,导弹出筒后逐渐衰减。风速为25 m/s时振幅最大,这表明风速的增大会导致发射筒x向振动的幅值增大。

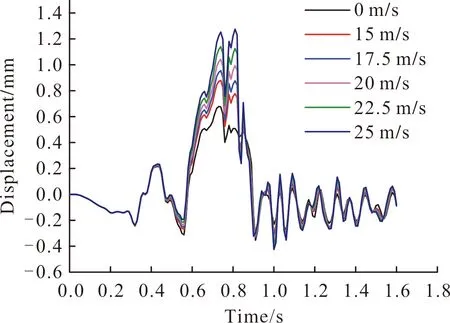
图12 不同风速下导弹发射筒口位移量Fig.12 Displacement of missile launch canister under different wind speeds

3.2 风载荷作用下发动机推力偏心角的影响分析

导弹发动机的推力偏心是导致发射偏差的重要原因之一,文中主要研究在风载荷作用下发动机推力偏心角对导弹发射精度的影响。如图13所示,该偏心角度以δ表示,z轴方向垂直于纸面向外,δ以逆时针为正。取风速为20 m/s,选取推力偏心角度δ分别为-0.2°、-0.1°、0°、0.1°和0.2°五种工况,分析导弹发射过程中姿态变化规律与发射筒振动情况。

图13 发动机推力偏心角示意图Fig.13 Schematic diagram of the engine thrust eccentricity angle

图14为不同发动机推力偏心角下导弹头部、质心与尾部在导弹发射过程中沿x方向位移曲线。导弹离筒前受到适配器导向作用的限制,位移较小;出筒后一段时间导弹的头部与质心处的位移随着发动机推力偏心角的增大而增大,而导弹的尾部位移随着偏心角的增大而减小。出现上述现象的原因是:发动机推力偏心角导致导弹底部存在一个x向的分量,从而使导弹质心受到一个z向的力矩,因此导弹在出筒后产生偏转。出筒0.6 s后导弹质心处位移分别为-82.95 mm、-11.56 mm、56.50 mm、126.65 mm、199.49 mm,可以看出在偏心角大小相同、方向相反的条件下,正向推力偏心角下的导弹质心位移幅值更大。这是因为正向推力偏心角下,导弹出筒后受到z负向的力矩向x正向偏转,同时由于导弹的推力随体,因此推力在x正向的分量增大,因此在同为x正向的风载荷的共同作用下,位移幅值较大;而负向推力偏心角下,推力在x负向的分量增大,而依然为x正向的风载荷阻挡了导弹向x负向运动,位移幅值较小。

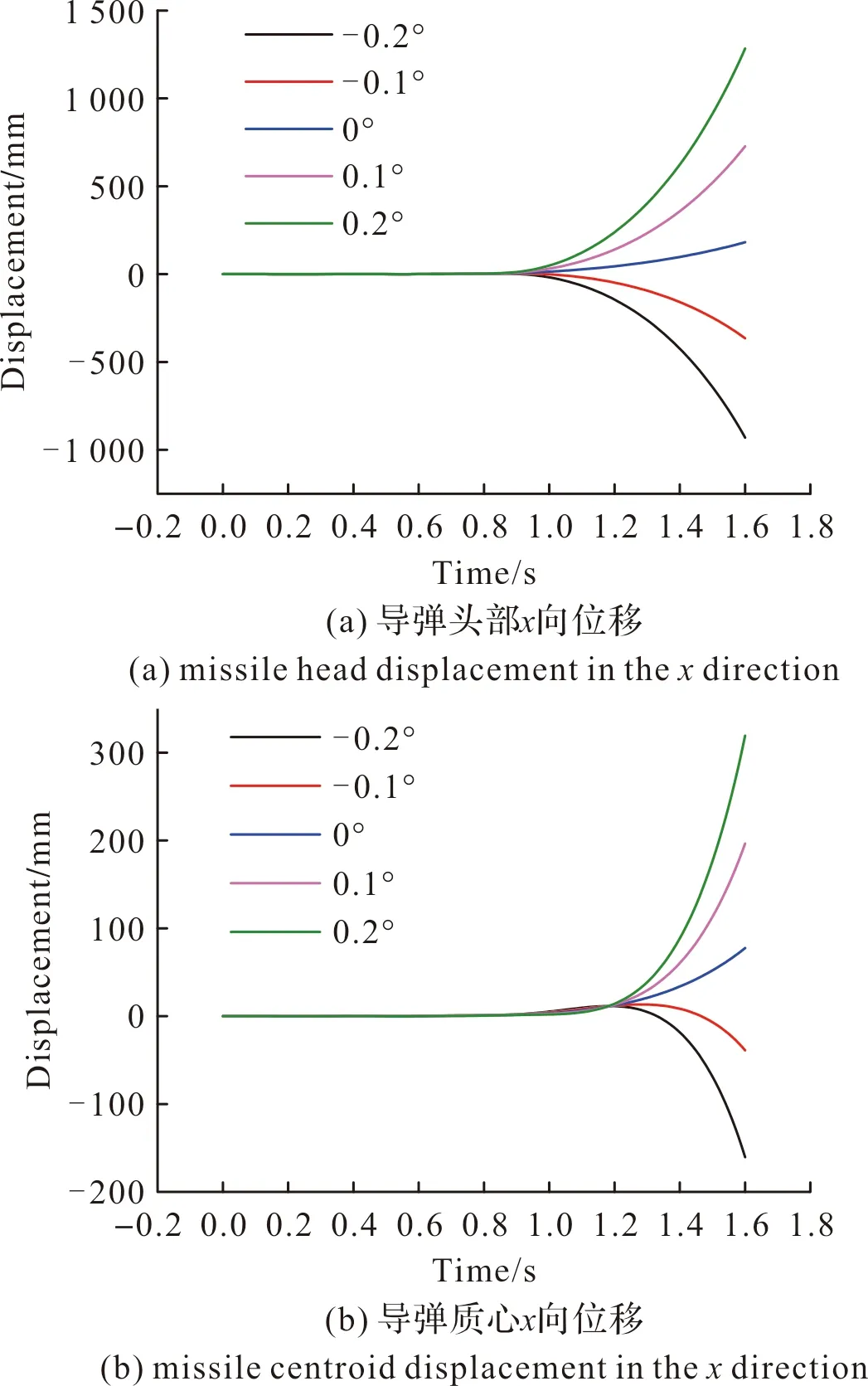
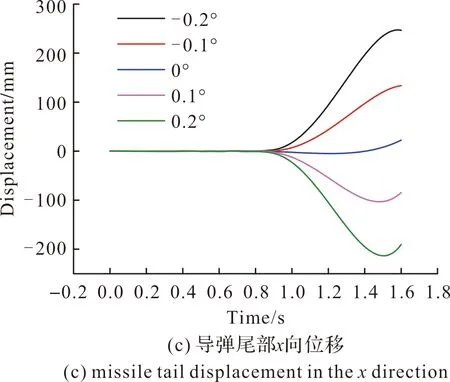
图14 不同δ下导弹头部、质心与尾部x向位移量Fig.14 x-direction displacement of missile head, centroid and tail under different engine thrust eccentricity angles

图15为不同发动机推力偏心角下导弹发射过程中质心俯仰角位移和俯仰角速度曲线。导弹在离筒时刻的俯仰角位移与俯仰角速度如表3所示。导弹离筒前受到适配器导向作用的限制,角位移和角速度较小;导弹出筒后,俯仰角位移和俯仰角速度随着发动机推力偏心角的增大而减小。

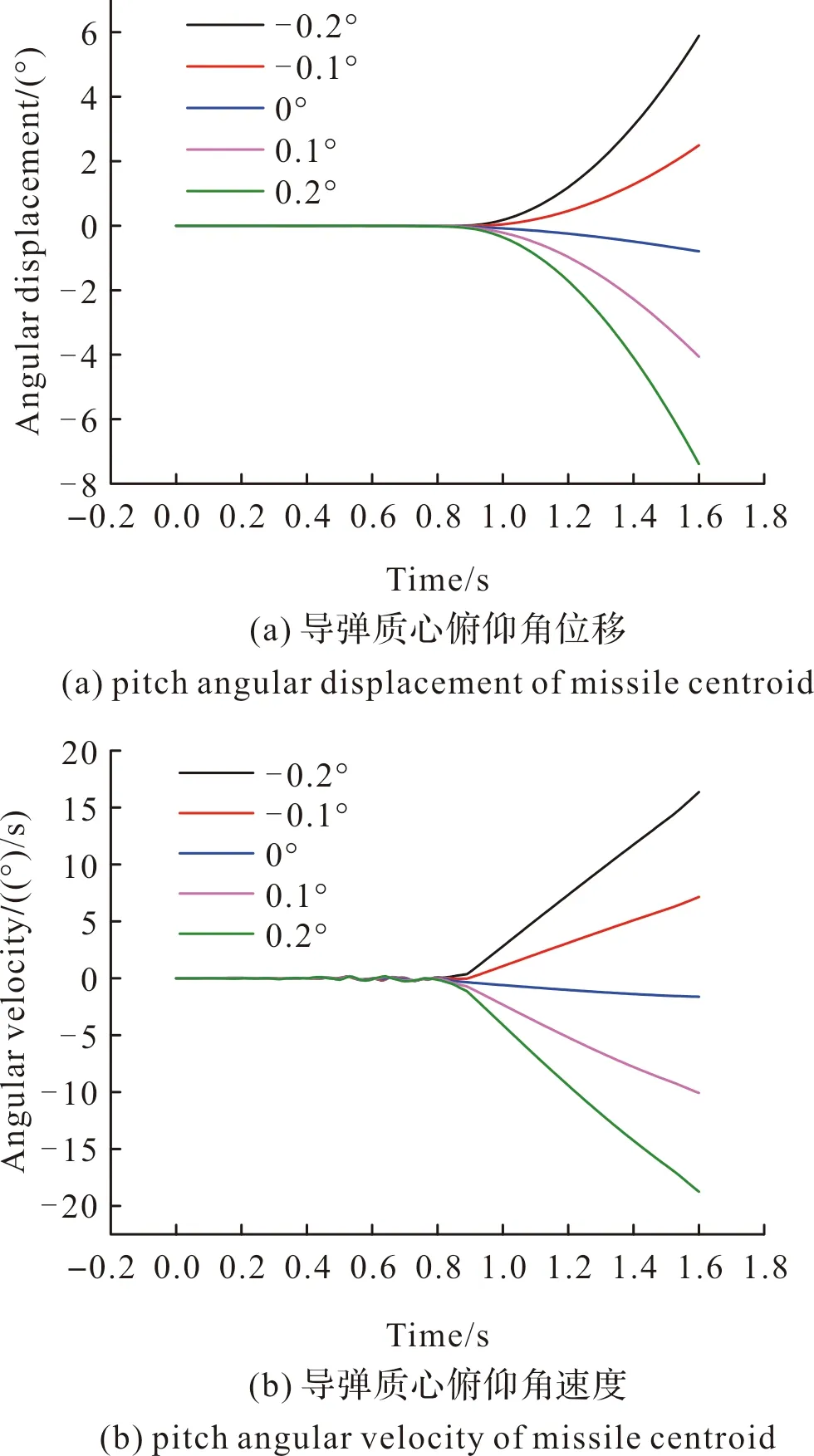
图15 不同δ下导弹质心俯仰角位移与俯仰角速度Fig.15 Pitch angular displacement and pitch angular velocity of missile centroid under different engine thrust eccentricity angles

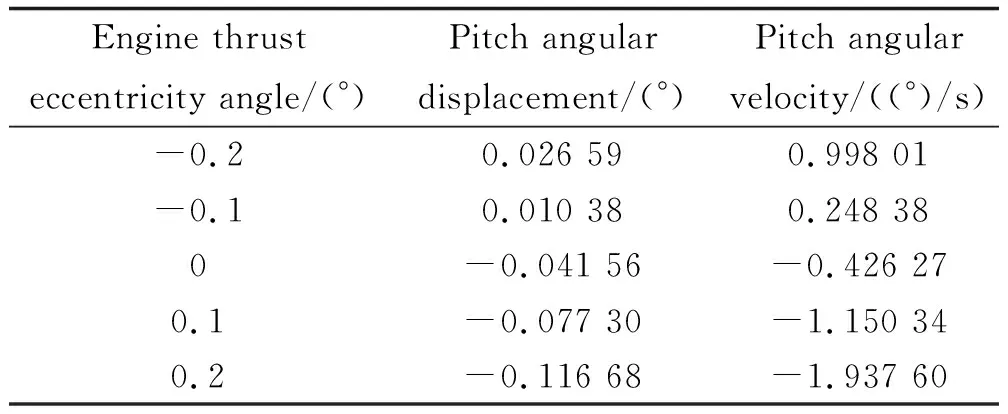
表3 不同δ下离筒时刻俯仰角位移与俯仰角速度Table 3 Pitch angular displacements and pitch angular velocities at the moment of departure from the cylinder under different engine thrust eccentricity angles

图16为不同发动机推力偏心角下发射筒在导弹发射过程中沿x方向位移曲线。发射筒在发射过程中反复振动,在0.9 s左右振幅最大,导弹出筒后逐渐衰减。推力偏心角幅值越大,发射筒的振幅越大。

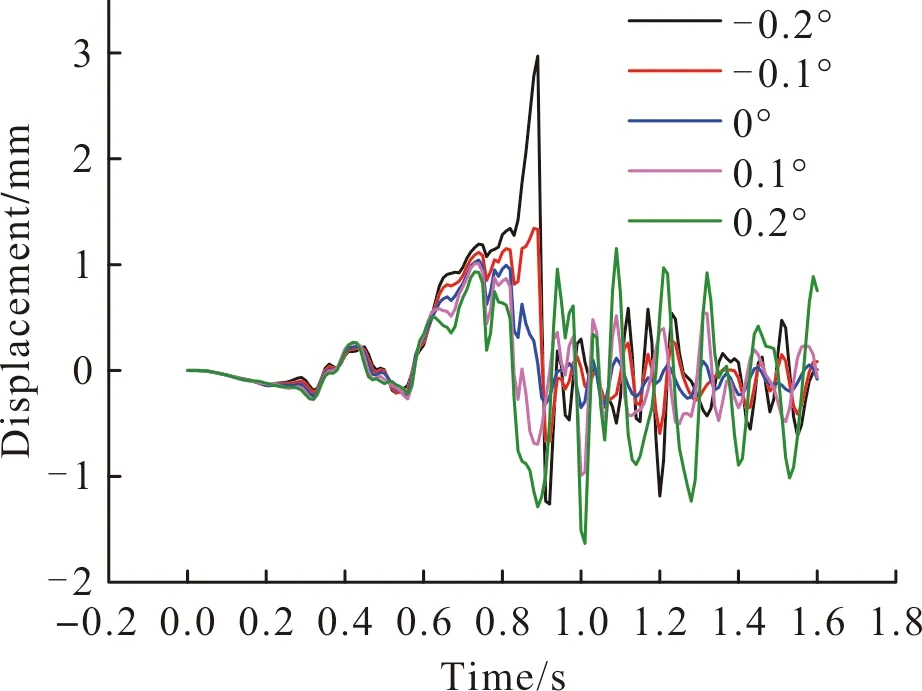
图16 不同δ下导弹发射筒口位移量Fig.16 Displacement of missile launch canister under different engine thrust eccentricity angles

3.3 风载荷作用下地面倾角的影响分析

发射场坪是影响车载导弹发射精度的重要因素,发射场坪的倾斜会导致车载导弹发射装置的整体倾斜,进而对发射过程中弹-车动态响应产生影响。下面主要研究在风载荷作用下发射场坪地面倾斜角度的影响。如图17所示,该偏心角度以γ表示,z轴方向垂直于纸面向外,γ以逆时针为正。取风速为20 m/s,选取推力偏心角度γ分别为-2°、-1°、0°、1°和2°五种工况,分析导弹发射过程中姿态变化规律与发射筒振动情况。

图17 地面倾斜角度示意图Fig.17 Schematic diagram of the ground inclination angle

图18为不同地面倾角下导弹头部、质心与尾部在导弹发射过程中沿x方向位移曲线。导弹离筒前受到适配器导向作用的限制,位移较小;出筒后一段时间后导弹的头部、质心与尾部处的位移均随着地面倾角的增大而减小。出筒0.6 s后导弹质心处位移分别为220.81 mm、137.99 mm、56.50 mm、-16.88 mm、-132.18 mm,可以看出在地面倾角大小相同、方向相反的条件下,负向地面倾角下的导弹质心位移幅值更大,这是因为当地面倾角为负的时候,属于背风坡,风载荷会加剧导弹向x轴正向上的偏移,位移幅值较大;而地面倾角为正时,属于迎风坡,风载荷会阻碍导弹向x轴负向上的偏移,位移幅值较小。

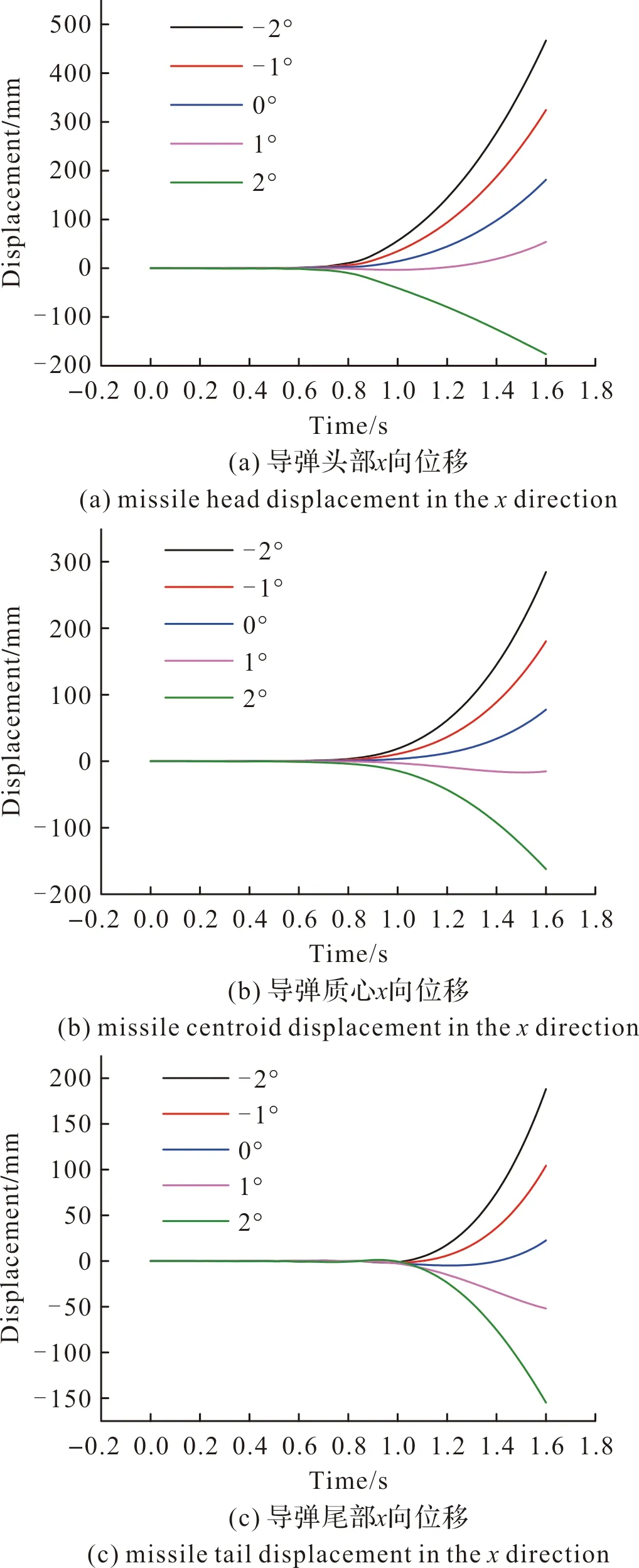
图18 不同γ下导弹头部、质心与尾部x向位移量Fig.18 x-direction displacement of missile head, centroid and tail under different ground inclination angles

图19为不同地面倾角下导弹发射过程中质心俯仰角位移和俯仰角速度曲线。导弹在离筒时刻的俯仰角位移与俯仰角速度如表4所示。导弹离筒前受到适配器导向作用的限制,角位移和角速度较小;导弹出筒后,俯仰角位移和俯仰角速度随着地面倾角的增大而减小。出筒一段时间后,由图可以看出导弹的俯仰角位移和俯仰角速度均随着时间的增大而减小,导弹的姿态在风载荷的作用下均向x正向偏转,这说明地面倾角对导弹的姿态影响较小,受风载荷影响较大。

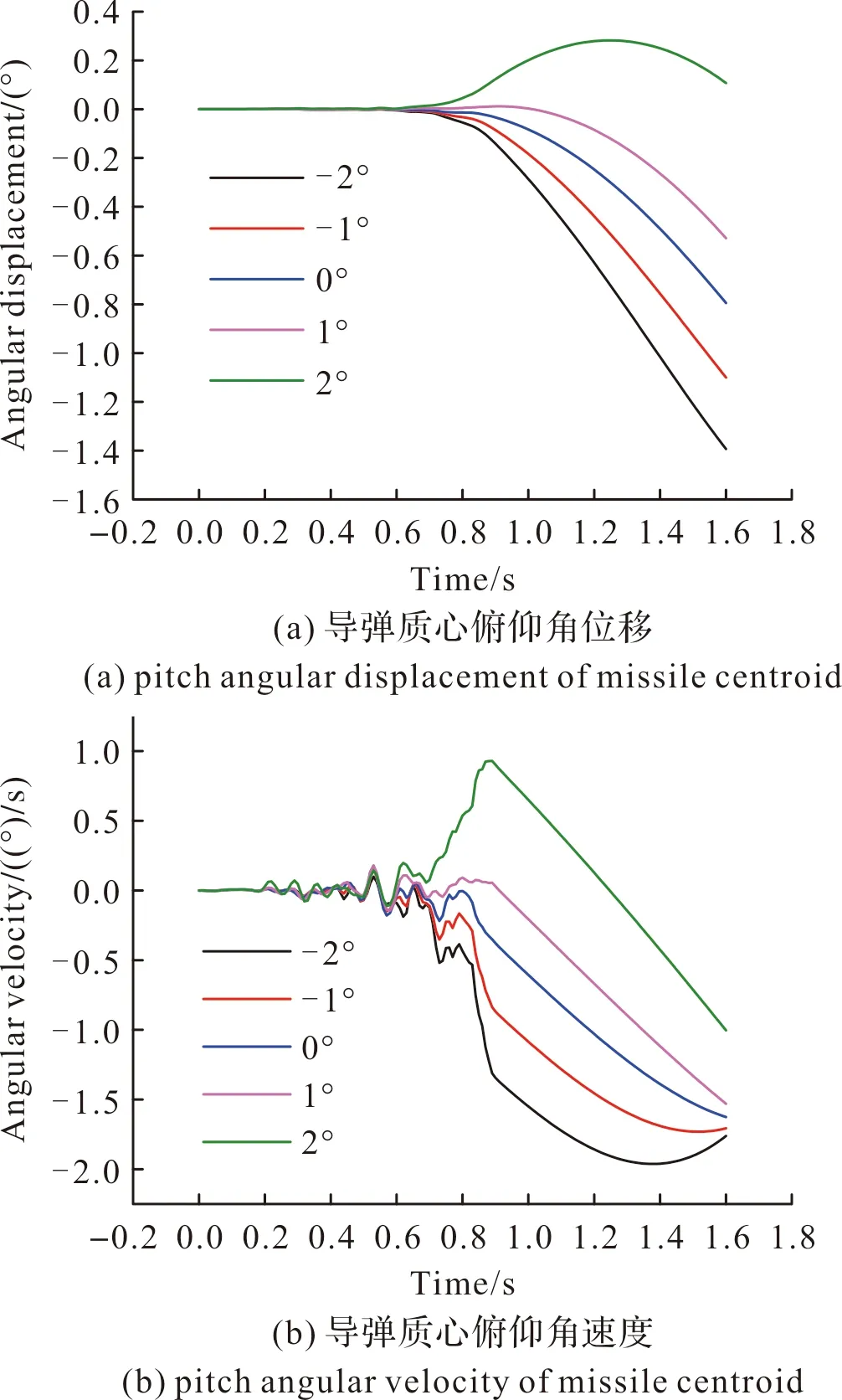
图19 不同地面倾角下导弹质心俯仰角位移与俯仰角速度Fig.19 Pitch angular displacement and pitch angular velocity of missile centroid under different ground inclination angles

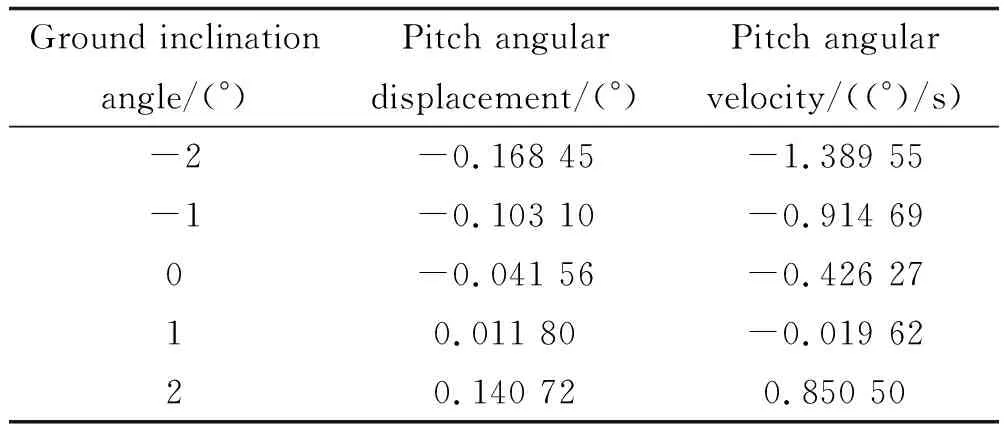
表4 不同γ下离筒时刻俯仰角位移与俯仰角速度Table 4 Pitch angular displacement and pitch angular velocity at the moment of departure from the cylinder under different ground inclination angles

图20为不同地面倾角下发射筒在导弹发射过程中沿x方向位移曲线。发射筒在发射过程中反复振动,导弹出筒后逐渐衰减。地面倾角幅值越大,发射筒的振幅越大;地面倾角大小相同、方向相反的条件下,负向倾角下的发射筒振幅更大。

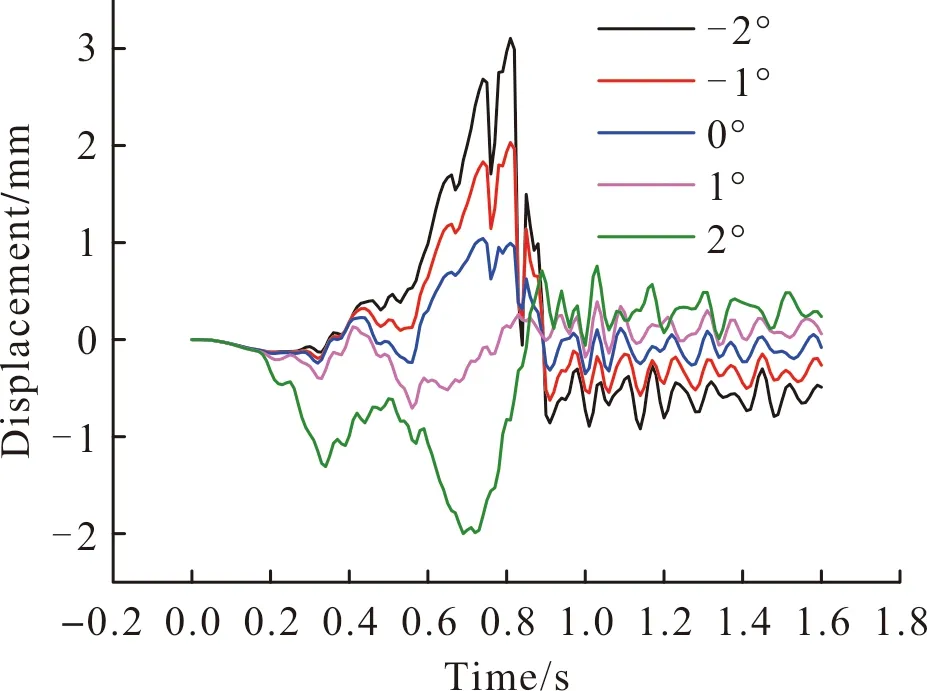
图20 不同发动机推力偏心角下导弹发射筒口位移量Fig.20 Displacement of missile launch canister under different ground inclination angles

4 结论

建立了车载导弹发射系统有限元模型,并创新地运用ABAQUS用户子程序进行联合二次开发,实现了随动风载荷的实时加载,基于该模型与方法分析了在不同风速、不同发动机推力偏心角和不同地面倾角下风载荷作用力对导弹姿态与发射筒振动的影响规律。所得结论如下:

1)创新地使用用户子程序接口实现随动风载荷的实时加载,该方法可以准确地模拟具有随动时变特性的风载荷,且可为其他动力学仿真中风载荷真实的模拟与加载提供参考。

2)风速在导弹出筒过程中与出筒后均对导弹影响较大,在出筒过程风载荷会使弹体以筒口适配器为支点做小幅杠杆运动;同时风速的增大会导致导弹沿风速方向的位移、角位移、角速度与发射筒沿风速方向的振幅显著增大,从而影响导弹发射精度。

3)发动机推力偏心角与地面倾角对导弹的发射姿态与发射筒振动有一定影响。其中,推力偏心角是引起发射精度偏差的主要原因,风载荷对推力偏心角或地面倾角引起的发射精度偏差有一定的促进或阻碍作用。

由于篇幅限制,并未对发射筒受风载作用的工况进行探究,同时还可以进一步研究发射过程适配器受力情况与风载荷对发射后适配器分离的影响。