基于RANSAC 算法的三轴磁通门传感器误差校正

罗建刚, 罗 骋,2, 李海兵,2, 刘静晓, 李海虎

（1. 青岛海洋科技中心, 青岛 266237;2. 北京航天控制仪器研究所, 北京 100039）

0 引言

三轴磁通门传感器可以测量磁场分量信息,其在军事和民用磁探测领域具有广泛的应用［1-3］。由于在材料、 加工和安装工艺等方面存在若干限制, 导致三轴磁通门传感器存在三轴非正交、 三轴标度系数不一致、 零点偏移等问题, 造成三轴磁通门传感器的测量值存在误差, 称之为转向误差［4-5］。 三轴磁通门传感器转向误差的存在影响了磁场分量和总场的测量精度, 为提高磁测精度, 在传感器使用之前必须对其转向误差进行校正。

国内外许多学者在三轴磁通门传感器转向误差校正算法方面进行了研究, 目前常用的校正算法有最小二乘法［6-7］、 椭 球 拟 合 算 法［8-9］、 遗 传 算法［4,10］、 神经网络算法［11］、 粒子群优化算法［12］、 差分进化算法［13］等。 上述文献所提出的算法都是基于使样本数据整体误差最小化的思想估算出误差参数, 当样本数据质量高、 无噪声或畸变数据点时, 上述算法可对转向误差起到良好的校正效果。但样本数据采集过程中难免会引入一些随机噪声或畸变数据点, 此时如果直接利用基于样本数据整体误差最小化的思想估算误差参数, 可能导致误差参数估算出现较大偏差, 达不到误差校正的要求。 通常样本数据中的含噪声或畸变数据点难以人为甄别和剔除, 或当样本数据量较大时, 人为剔除比较费时费力, 不利于外场环境下执行快速校正工作。

针对上述问题, 本文在椭球拟合算法的基础上提出了基于随机抽样一致性（Random Sample Consensus, RANSAC）算法的三轴磁通门传感器误差校正方法。

1 三轴磁通门传感器误差分析

由于加工和安装工艺上的限制, 三轴磁通门传感器三个敏感轴之间并非完全正交, 由此对空间磁场测量造成的误差称为非正交误差, 如图1 所示; 磁传感器三个敏感轴之间灵敏度和放大调理电路可能存在差别, 导致三个轴在测量相同的磁场时其输出值可能不同, 此项误差称为标度系数误差; 三轴磁通门传感器本身含有一些铁磁性物质, 其会产生剩磁, 此外, 信号放大电路也会产生零点漂移, 由此造成的误差称为零偏误差。 综合考虑上述各项误差, 可建立三轴磁通门传感器测量误差模型

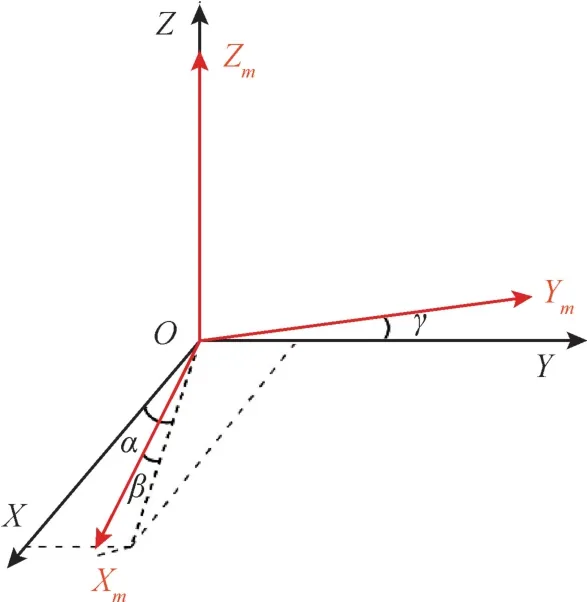
图1 磁传感器坐标轴非正交示意图Fig.1 Schematic diagram of the magnetic sensor non-orthogonal axis

由于非正交角α、β、γ均为小角度, 故有cosα≈1、 cosβ≈1、 cosγ≈1、 sinα≈α、 sinβ≈β、sinγ≈γ, 则矩阵A可简化为

矩阵K和A均为严格对角占优矩阵, 因此其为可逆矩阵。 对式（1）变换可得到三轴磁通门传感器误差校正模型

三轴磁通门传感器的误差参数bx、by、bz、kx、ky、kz、α、β、γ在短时间内可看作是定值, 若能求得上述9 个误差参数值, 便可根据式（2）实现三轴磁通门传感器误差校正, 三轴磁通门传感器误差校正问题转化为上述9 个误差参数的估算问题。

2 三轴磁通门传感器误差校正

2.1 基于传统椭球拟合算法的误差参数估算

在理想情况下, 三轴磁通门传感器在总场模值为‖B0‖的均匀磁场环境中转动时, 其磁场测量点Bm（i）（i=1, 2, …,n）应分布在以‖B0‖为半径、 球心位于坐标原点的球面上。

令三轴磁通门传感器在总场模值为‖B0‖的磁场环境中转动采集数据, 对式（2）两边分别取平方, 应有

式（3）可改写为如下形式

在数学中, 二次曲面的一般形式可表示为

式（5）中,为二次曲面的参数向量,η= ［x2y2z22xy2xz2yz2x2y2z1］T为曲面上某点坐标（x,y,z）构成的向量。 对于 空间某 点（x′,y′,z′） 而言,F（ξ,η′）的值表示该点到曲面F（ξ,η） =0 的代数距离。

若要求取一组磁场测量点Bm（i）（i=1, 2, …,n）所在的椭球曲面, 可以所有测量点到待求椭球曲面代数距离平方和最小的方式拟合计算出最佳的椭球曲面参数ξ, 即

式（6）中,ξ为待求的椭球参数向量,ηm（i）和D分别为磁场测量点构成的向量和矩阵, 有

为保证式（6）的拟合结果为椭球曲面, 需要加入椭球约束条件

式（7） 中, 应同时满足I=a1+a2+a3和J=。

联合式（6）、 式（7）, 可得到基于样本数据Bm（i）（i=1, 2, …,n） 的最佳椭球参数向量ξ。 结合式（4）和式（5）, 有

但上述误差参数求取过程是基于使样本数据整体误差最小化的思想进行的, 当样本数据含有噪声或畸变数据点时, 会导致传感器误差参数估算出现偏差。

2.2 基于RANSAC 算法的误差参数估算

RANSAC 是一种稳健的模型参数估计算法, 它由Fischler 和Bolles 于1981 年 最 先 提 出［14-15］。RANSAC 算法不同于椭球拟合等一般估计算法利用所有样本点进行模型参数估算, 它首先通过多次随机抽样计算的方式剔除噪声或畸变数据点,然后再利用剩余的正常样本数据估算模型参数［16］。

在椭球拟合算法的基础上, 利用RANSAC 算法对三轴磁通门传感器的误差参数进行估算, 步骤如下:

步骤1: 令磁传感器在总场模值为‖B0‖的均匀磁场环境中转动, 采集样本数据Bm（i） （i=1,2, …,n）, 其中样本数据个数n≥150。 设定迭代累加变量为k,k的初始值为1。

步骤2: 从样本数据集Bm中随机抽取样本数据子集B′m（kj）（j=1, 2, …,q）, 样本数据子集个数为q, 其满足9≤q≤n/10。

步骤3: 把B′m带入2.1 节中的椭球拟合算法进行误差参数估算, 得到误差校正矩阵D（k）和向量b（k）,通过式（2） 对样本数据Bm（i） 进行误差校正,校正后的磁总场模值为。

步骤4: 令

若有-ε≤η（ki）≤ε, 则认为Bm（i）为局内点,将其保存至数据集P（k）; 否则认为其是局外点,不保存; 令累加变量k=k+1。

步骤5: 重复执行步骤2 ～步骤4 共K次, 即k=1, 2, …,K, 统计每次迭代计算所保留局内点的个数s（k）=size（P（k））, 选取s（k）最大值所对应的局内点作为最终样本数据。

步骤6: 把最终样本数据带入2.1 节中的椭球拟合算法, 估算出三轴磁通门传感器的误差参数。

在RANSAC 算法抽样计算过程中, 当某次抽取的样本数据含噪声或畸变点较多时, 会使校正模型出现偏差, 导致大部分数据成为局外点;当抽取的样本数据都为正常数据点时, 会得到理想的校正模型, 此时可保证大部分正常数据点成为局内点, 而噪声和畸变数据则呈发散状, 只有极少数可以成为局内点。 通过多次随机抽样, 可保证最终的样本数据基本不含噪声或畸变数据点。

偏差阈值ε的取值至关重要, 取值过大会使噪声点成为局内点, 取值过小则可能使正常数据点成为局外点。 根据经验, 可令ε取值为为全部样本数据直接利用2.1 节中椭球拟合算法校正后磁总场的标准差

关于迭代次数K的取值, 假定样本数据中正常数据点的比例为ω, 每次抽取的样本子集个数为q, 那么进行K次抽样后至少有一次抽取的全为正常数据点的概率为

式（10）中,f为置信概率, 通常情况下f可取值为99.99%, 此时可计算出迭代次数K的最小取值

3 仿真分析与实验验证

3.1 仿真分析

为了验证RANSAC 算法的有效性, 本文进行了仿真分析。

设置环境磁总场强度为50000nT, 三轴磁通门传感器的误差参数如表1 所示。 令三轴磁通门传感器在磁场空间中转动采集一组样本数据, 样本数据包含200 个数据点, 其空间分布如图2 所示。 对样本数据中10% 的数据加入均值为0、 方差为500nT 的高斯白噪声作为噪声点或畸变数据点,图3 为磁总场曲线对比。

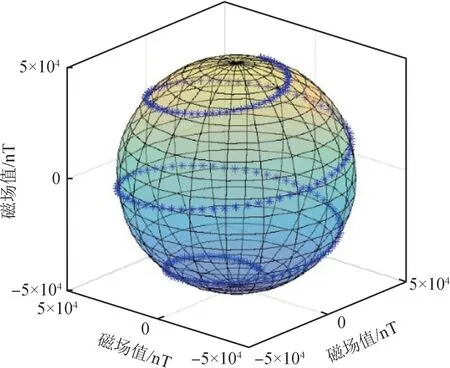
图2 磁场数据点的空间位置分布Fig.2 Spatial position distribution of magnetic field data points

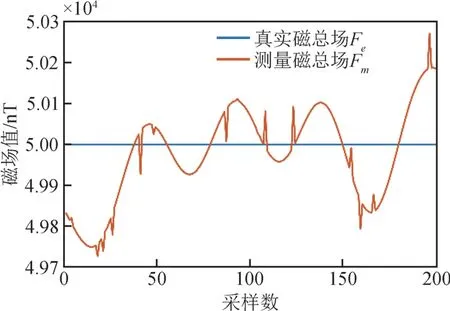
图3 磁总场曲线对比Fig.3 Comparison of total magnetic field curves

表1 仿真计算中RANSAC 算法参数设置Table 1 Parameter setting of RANSAC algorithm in simulation calculation

分别采用一般椭球拟合算法和RANSAC 算法对样本磁场数据进行误差参数估算, RANSAC 算法的参数设置如表1 所示。 其中,ω为样本数据中正常数据点的比例,q为每次迭代计算抽取的数据个数,ε为偏差阈值,K为迭代次数。 两种算法误差参数估算结果如表2 所示。 其中, EF 表示椭球拟合算法, RS 表示RANSAC 算法。

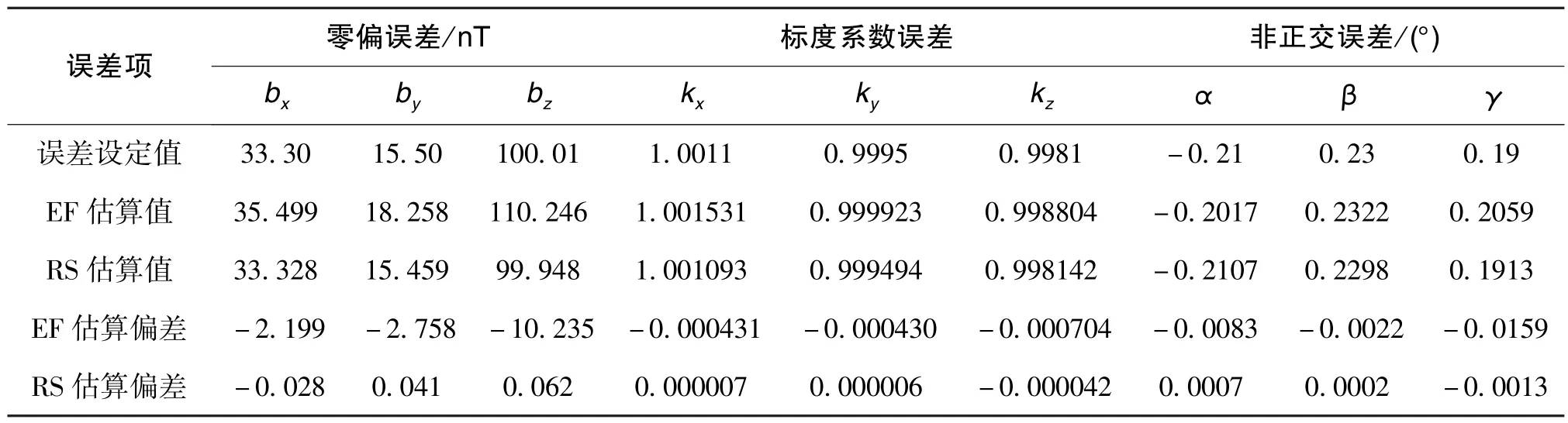
表2 两种算法对误差参数的估算结果Table 2 Estimation results of error parameters by two algorithms

通过对比, 相比于一般椭球拟合算法,RANSAC 算法对误差参数的估算精度显著提升, 对零偏误差、 标度系数误差的估算精度提升了2 个数量级, 对非正交误差的估算精度提升了1 个数量级。 以上仿真结果说明, RANSAC 算法具有更强的适用性, 对于含噪声或畸变数据的样本数据, 其仍然能够估算出更为准确的误差参数。

3.2 实验验证

为检验RANSAC 算法在实际中的应用效果,本文设计了外场实验, 实验设备主要有三轴磁通门传感器、 数采计算机、 上位机、 三轴无磁转台、质子磁力仪等。

（1）直接实验

利用结构件将三轴磁通门传感器安装在三轴无磁转台上, 如图4 所示。 对转台进行一系列旋转, 使三轴磁通门传感器尽可能多地遍历空间姿态。 采集一组样本数据, 样本数据共包含430 个数据点, 其磁总场曲线如图5 所示。 由于传感器的性能和环境干扰磁场的影响, 样本数据中包含部分噪声或畸变数据点。 经计算, 样本数据的峰峰值为575.7nT, 标准差为96.2nT。 另外, 利用质子磁力仪测量背景磁场强度作为误差校正的目标值。

图4 数据实测现场图Fig.4 Diagram of data field measurement

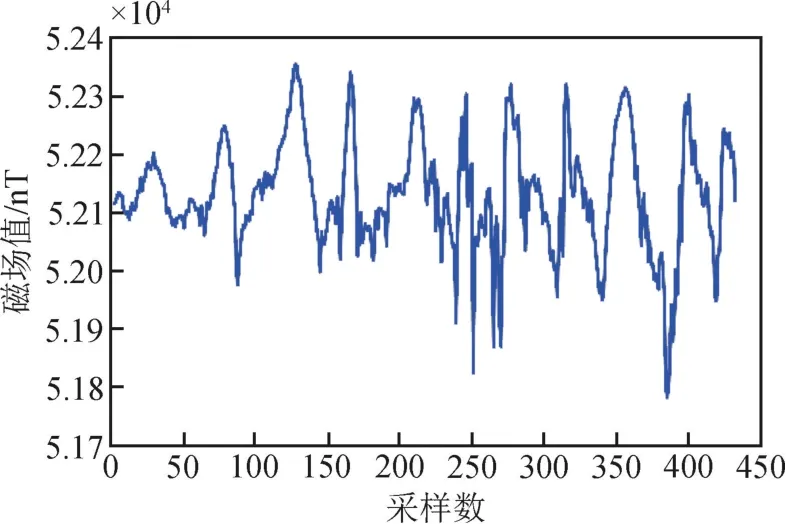
图5 实测磁总场曲线Fig.5 Curve of measured total magnetic field

分别利用椭球拟合算法和RANSAC 算法对上述样本磁数据进行误差参数估算和误差校正。RANSAC 算法的参数设置如表3 所示, 两种算法误差参数估算结果如表4 所示, 两种算法对样本数据误差校正前后的总场曲线对比如图6、 图7 所示,样本数据校正后总场的峰峰值和均方根误差（RMS）对比如表5 所示。

表3 实验中RANSAC 算法参数设置Table 3 Parameter setting of RANSAC algorithm in the experiment

表4 两种算法估算的误差参数对比Table 4 Comparison of error parameters estimated by two algorithms

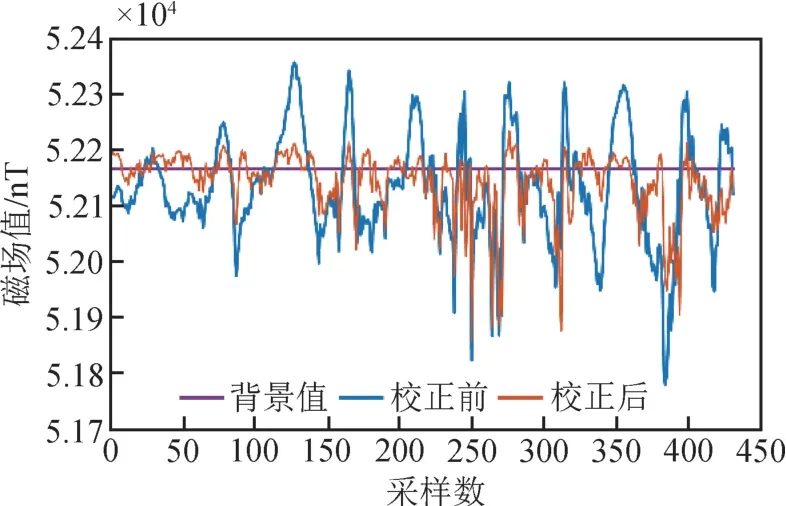
图6 椭球拟合算法磁总场校正前后对比Fig.6 Comparison of ellipsoid fitting algorithm before and after total magnetic field correction

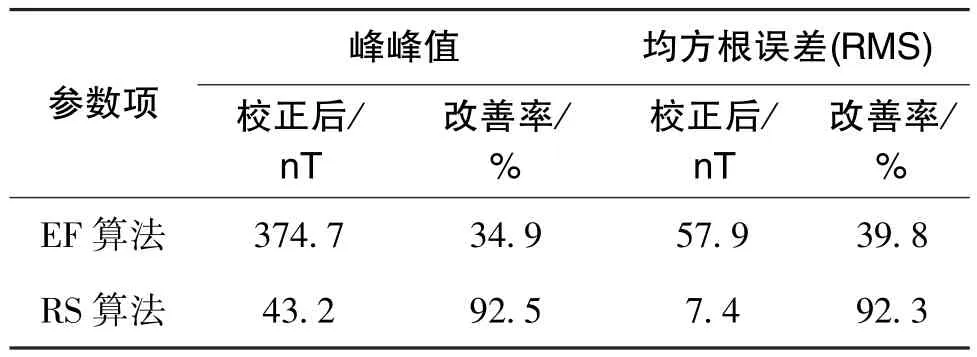
表5 磁总场校正前后参数对比Table 5 Comparison of parameters before and after total magnetic field correction

对比上述结果, 椭球拟合算法对样本数据进行校正后, 总场数据的峰峰值和均方根误差（RMS）获得了改善, 但由于样本数据中含有噪声或畸变数据点, 导致校正效果并不理想; RANSAC 算法通过多次随机抽样的方式剔除了可能含有噪声或畸变的205 个数据点, 利用剩余的225 个数据点估算出了误差参数, 最后对剩余的样本数据进行误差校正, 校正效果更加明显。 相比于椭球拟合算法,RANSAC 算法校正后, 样本数据总场的峰峰值和均方根误差（RMS） 的改善率分别提高了57.6%和52.5%。

（2）对比实验

为了进一步评估两种算法对误差参数估算的准确性, 利用同一个三轴磁通门传感器另外采集一组样本磁场数据（341 个数据点）, 该组数据的峰峰值和均方根误差（RMS） 分别为270.9nT 和92.1nT。 利用表4 中的两组误差参数分别对该组样本数据进行校正, 校正前后磁总场曲线对比如图8所示, 校正后磁总场的峰峰值和均方根误差（RMS）值及其改善率如表6 所示。

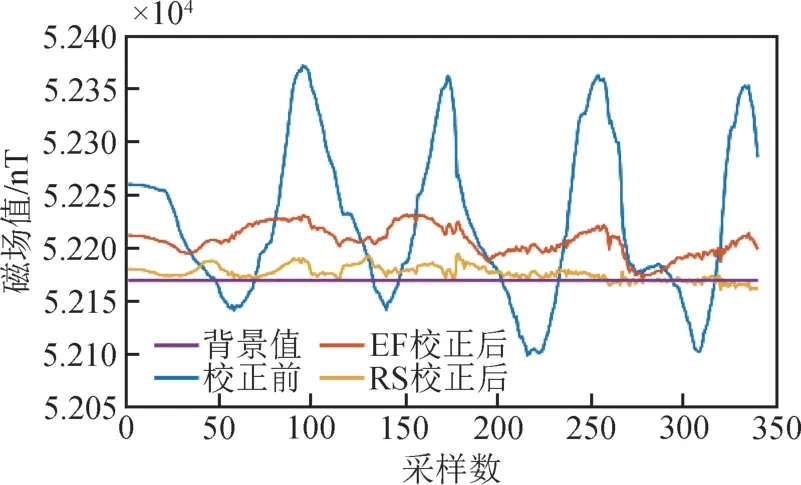
图8 对比实验磁总场曲线对比Fig.8 Comparison of total magnetic field curves in comparison experiment

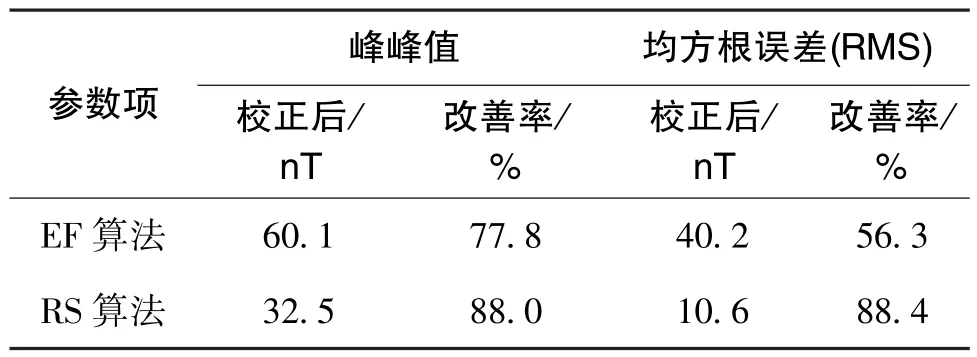
表6 对比实验磁总场校正前后参数对比Table 6 Comparison of parameters before and after total magnetic field correction in comparison experiment

对比上述结果, 利用两组误差参数分别对该组样本数据进行校正后, 磁总场数据的峰峰值和均方根误差（RMS）均获得明显改善, 但RANSAC 算法所得误差参数较椭球拟合算法所得误差参数对样本数据的校正效果更加明显, 磁总场的峰峰值和均方根误差（RMS）的改善率分别提高了10.2%和32.1%。 通过上述结果可以认为, 相比于椭球拟合算法, RANSAC 算法具有更强的适用性, 当样本数据含有噪声或畸变数据点时, 其仍然可以估算出更为准确的误差参数。

4 结论

本文在椭球拟合算法的基础上提出了基于RANSAC 算法的三轴磁通门传感器误差校正方法,该方法通过多次随机抽样的方式剔除样本数据中的噪声和畸变数据点, 最终估算出更加准确的误差参数。 仿真分析中, 在样本数据含有噪声时,所提出的方法可以剔除噪声点并估算出准确的误差参数, 相比于传统方法, 误差参数估算精度提升了1 ～2 个数量级; 外场实验中, 所提出的方法对实测数据误差校正效果更加优良, 磁总场的峰峰值和均方根误差（RMS）的改善率较传统算法分别提高了10.2%和32.1%。 综合分析认为, 所提出的方法更加适用于外场环境下执行三轴磁通门传感器转向差的快速校正工作, 具有一定的工程应用价值。