突破思维定式 感受多样“聚焦”——例析特殊边界的“磁聚焦”问题

张 振

(浙江省宁波市鄞州高级中学)

“磁聚焦”是高中物理习题中常见的一类模型,其中最常见的经典模型如图1,平行射入圆形有界磁场的相同带电粒子,如果圆形磁场的半径与轨迹圆的半径相等,则所有粒子都从磁场边界上的同一点射出,反之还有“磁发散”如图2。

图1

图2

然而在实际教学中发现,无论是教师讲授还是各类试题,“磁聚焦”模型几乎都是上述这种经典的圆形边界,这样很容易让学生误认为磁聚焦只有这种情况,从而使学生形成思维定式,在练习或考试中一旦遇到非此模型的聚焦问题,就会束手无策或者胡乱套用。为突破学生思维定式,笔者在教学中通过实例,进行归类分析,列举了几种特殊边界的“磁聚焦”模型,很好地拓展了学生思维,提升物理核心素养。

一、组合型边界实现聚焦

除了正圆形边界,通过不同形状边界的组合,也能实现类似的“磁聚焦”和“磁发散”效果,该类试题多次在宁波市高三模拟考试中出现,下面举例说明。

图3

(1)粒子在磁场中运动的半径r;(r=0.08 m)

(2)从最上端M点发射的粒子恰好进入有界磁场,求该粒子在磁场中的运动时间t(保留两位有效数字);(t=3.3×10-7s)

(3)有界磁场边界Ⅱ的轨迹方程。

图4

【点评】本题为宁波市一模统考题,作为模考压轴题,看似跟经典模型很像,实则大有区别,此时磁场大圆半径不等于轨迹圆半径,不能套用经典模型。学生由于思维定式又缺乏临场分析能力,因此得分普遍较低。该题也告诉我们,通过构造一个无磁场区域的圆形边界,与圆形磁场边界组合,依然能实现聚焦。同时该题要求学生掌握求轨迹方程的一般方法,即设轨迹上某点坐标(x,y),通过几何关系找到两者之间的关系。

本题也可以拓展为“磁发散”模型,从O点沿各个方向发射速度大小相同的带正电荷的粒子,粒子在该匀强磁场中的偏转半径均为0.08 m,如图5所示,由几何关系可知PO=FO1=0.08 m,FP=O1O=0.1 m,因此四边形FPOO1为平行四边形,故FO1∥PO,FO1为竖直,从而得到从第Ⅰ象限出射的粒子速度方向均沿x轴正方向。

图5

【例2】(2021年浙江宁波一模)如图6所示,半径为r的半圆abc内部没有磁场,半圆外部空间有垂直于半圆平面的匀强磁场(未画出),比荷为p的带电粒子(不计重力)从直径ac上任意一点以同样的速率垂直于ac射向圆弧边界,带电粒子进入磁场偏转一次后都能经过直径上的c点并被吸收,下列说法正确的是

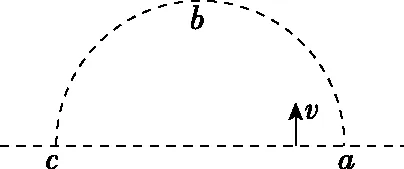
图6

( )

A.磁场方向一定垂直半圆平面向里

B.带电粒子在磁场中运动的轨迹半径为2r

图7

【答案】C

【点评】该题粒子垂直于ac射向圆弧边界,进入磁场偏转一次后都能经过直径上的c点,此时边界也不是经典圆形。本题边界特殊,但分析过程中构建菱形的思想来自于经典模型,很好的考查了学生的知识迁移能力。

【例3】(2020年浙江宁波二模)如图8所示,平行于直角坐标系y轴的PQ是用特殊材料制成的,只能让垂直打到PQ界面上的电子通过,且通过时并不影响电子的速度。其左侧有一直角三角形区域,分布着方向垂直纸面向里、磁感应强度为B的匀强磁场,其右侧有竖直向上且场强为E的匀强电场。现有速率不同的电子在纸面上从坐标原点O沿不同方向射到三角形区域,不考虑电子间的相互作用。已知电子的电荷量为e,质量为m,在△OAC中,OA=a,θ=60°,D为x轴上的一个点,且OD=4a。求:

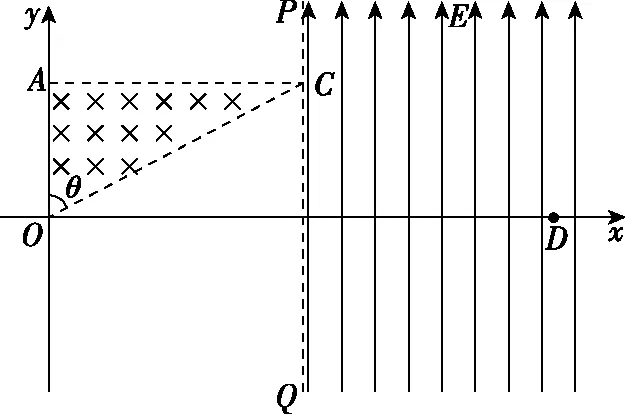
图8

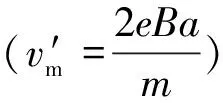
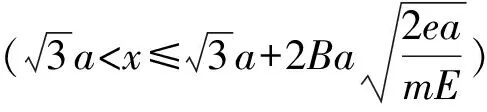
(4)现把PQ右侧电场撤去,增加一垂直纸面向里、磁感应强度为2B的矩形匀强磁场,使通过PQ界面的电子汇聚于D点,求该矩形磁场的最小面积。

图9

【点评】磁聚焦模型一般都要求粒子沿各个方向发射的速率相同,若粒子速率各不相同又如何实现磁聚焦和磁发散呢,本题很好地给出了一种方案。该题并未使用圆形边界或者圆形组合式边界模型,而是通过构建三角形和矩形磁场,同时实现磁发散和磁聚焦,可谓非常巧妙,本题作为宁波市二模的压轴题,很好地考查了学生的物理学科思维,具有较好的区分度。

二、对称型边界实现聚焦

带电粒子在磁场中运动往往存在对称美,同样利用合适的对称型边界也能实现带电粒子的聚焦,下面举例说明。

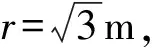
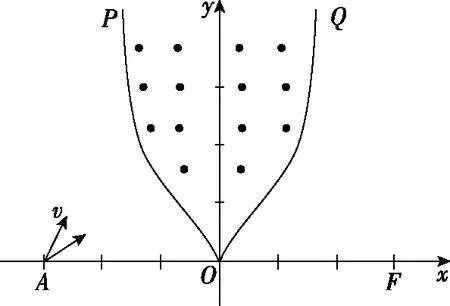
图10

图11

【点评】该题模型比较新颖,带电粒子从某点发散后再次实现聚焦,不一定需要两个圆形磁场的组合,而是通过特殊的对称型边界,就能满足聚焦效果,而且更具有普遍意义。本题通过寻找几何关系,找到x与y的联系点,求解边界方程,也是常用的数学方法之一,需要学生有较好的数学水平,也体现了学科核心素养中对数学能力的要求。

【例5】离子注入系统是一种对半导体进行掺杂的方法,可以改变半导体材料的成分和性质。如图12是它的简化示意图,由离子源、加速器、质量分析器、磁偏转室和注入靶组成。初速度近似为0的正离子从离子源飘入加速器,加速后的成为高能离子,离子沿质量分析器的中轴线运动并从F点射出,然后垂直磁偏转室的边界从P点进入,离子在磁偏转室中速度方向偏转90°后垂直边界从Q点射出,最后垂直打到注入靶上。已知质量分析器的C、D两极板长为L;磁偏转室内部为匀强磁场,圆心为O,O与P之间的距离为L;不考虑离子的重力及离子间的相互作用。假设质量分析器两极板间电势差发生极小的波动,则正离子在质量分析器中不再沿直线运动,但可近似看成是匀变速曲线运动。要使这些离子经磁偏转室后仍能全部会聚到一点,求P点与F点之间的距离h。

图12

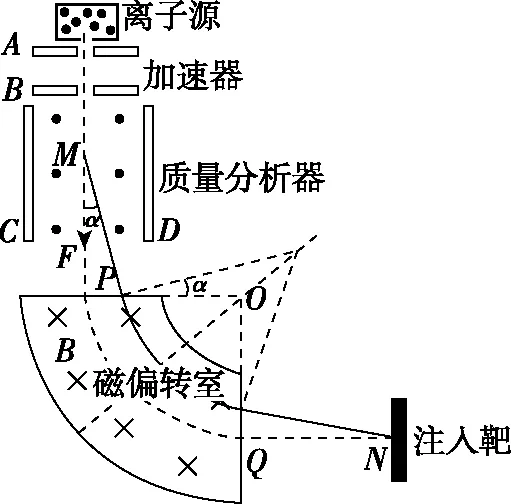
图13

【点评】该题基于实际情境,而实际问题中往往没有特别理想的状态,比如该题由于质量分析器两极板间电势差发生极小的波动,使正离子在质量分析器中不再沿直线运动,需要让学生通过分析,找到合理位置放置偏转磁场,从而实现聚焦,该题关键是运用平抛运动相关规律和粒子在磁场中运动的对称性,通过寻找各物理量之间的几何关系求得h,对数学能力有较高要求。

三、螺旋式轨迹实现周期性聚焦

带电粒子在磁场中运动的问题,在高中阶段大多以二维平面问题出现,若是在三维空间运动,就对学生的思维提出了更高的要求,近年来各地高考真题和模拟题中,都有立体空间运动模型的呈现,该类题型能更好地改善学生对物理学习的局限性,提升学生空间思维能力,下面举一例说明在三维空间下的磁聚焦模型。

【例6】利用带电粒子在匀强磁场中做螺旋线运动的回旋周期与粒子速率无关的特性,可以实现对带电粒子的聚焦,现将聚焦简化成如下的过程:大量电子从M板上的小孔飘入(认为初速度为零)M、N两板间的加速电场中,并从N板上的小孔飞出,由于电子之间的相互排斥作用会让电子在从电场中飞出时散开一个极小的角度θ,如图14所示。考虑同时从N板小孔中飞出的电子在离开电场区域后直接进入匀强磁场区域中,由于磁场的作用会在磁场内再次聚焦。已知加速电场的电压为U,板间距离为d,匀强磁场沿水平方向、磁感应强度大小为B,电子的电荷量为-e,质量为m。电子之间的相互作用很小可以忽略其对电子速度大小的影响,不考虑电子之间的碰撞,当角度极小时可以认为sinθ≈θ,cosθ≈1,欲使电子刚好在会聚点离开磁场,则磁场的左右两侧间的宽度l应满足什么条件。

图15

【点评】螺旋运动是物理中一种常见的运动,但日常练习所涉及的题并不多,在磁场中当带电粒子速度方向与匀强磁场方向不垂直时,往往就表现为螺旋运动。该题巧妙利用这个特点,设计了磁聚焦模型,实现周期性聚焦,难度不大但模型经典,既考查了运动的合成和分解问题的处理能力,又培养了学生的空间思维。

四、小结