例析相对圆周运动向心力的求解
2023-04-15林厦门
林厦门
(福建省漳州市教育科学研究院)
1 问题的提出
新高考内容改革强调在考试中创新考试形式、加强教考衔接,防止试题形式固化,保持试卷难度稳定。分步骤稳妥调整试题试卷形式,减少考试固化给机械训练和大量刷题带来的收益。创新命题方式,注重能力考查是新高考的必然趋势。因此,一线教师在教学中应注重学科知识的融会贯通、各种方法的灵活运用,引导学生掌握原理、内化方法。
相对运动在近几年的高考题中不时出现,例如2022年福建高考计算压轴题及2022年湖南高考第8题都涉及相对运动的有关知识。相对运动较为抽象,在非惯性系中相对圆周运动的向心力求解更是令人难以理解,该知识点在教学中又容易被忽视,所以一旦出现此类试题,学生常常束手无策。本文通过精选例题,由浅入深对相对圆周运动问题进行全面剖析,逐步厘清解题的思维障碍,引发思考。
2 惯性系中相对圆周运动向心力的求解
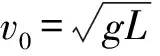
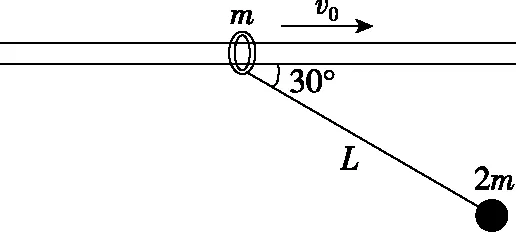
图1

【评析】思维定式在习惯上也被称作思维上的“惯性”,它能够影响后续活动的趋势。有些学生死记硬背,不加思考乱套公式,小球对地并非做圆周运动,细线拉力对小球做功不为零,小球机械能不守恒,最低点速度v的值求解有误。还有部分学生会将最低点速度v直接代入向心力公式,导致错误。小球相对滑环才是圆周运动,因此,应选滑环为参考系,用相对滑环的速度进行求解。根据题设条件无法求解最低点速度,最低点速度是确定的,更不能随意假设而导致科学性错误。
例1中滑环做匀速运动,是惯性系,要注意机械能是否守恒,且避开“相对速度”这一陷阱即可求解圆周运动的向心力。
3 非惯性系中相对圆周运动向心力的求解
【拓展1】在例1中,若释放小球的同时不对滑环施加外力,而是让它们同时无初速度释放,则当小球第一次运动到最低点时,细线拉力F多大?

【评析】有人认为小球运动过程中,滑环始终受到细线的拉力作用,滑环做变速运动,是非惯性系,应考虑惯性力,上述的解法应该有问题,其实是多虑了。小球运动到最低点时细线处于竖直状态,此瞬间细线对滑环的拉力方向竖直向下,滑环所受合力为零,加速度为零,惯性力也是零,对向心力求解无影响。因此以滑环为参考系,无需考虑惯性力。


图2
【原解析】P刚要脱离滑板时,在水平方向P与滑板共速,设速度为v1,P速度为vC,由水平方向动量守恒定律得
mv0=(2m+m)v1①
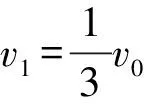
由能量守恒定律得
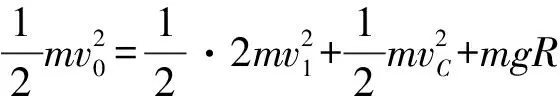
设P刚要脱离滑板时竖直方向的速度为v2,如图3所示,根据速度关系得

图3
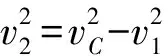
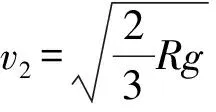
P水平方向受力如图4所示,由牛顿第二定律得

图4
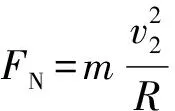

【评析】朱熹说过:“学贵有疑,小疑则小进,大疑则大进”。疑是思维的开始,是创新的基础,心理学研究表明,意识到问题的存在是思维的起点,正所谓“疑是思之初,学之端”。原解析解题思路似乎无懈可击,认为P相对滑板做圆周运动,只要利用P相对滑板的速度v2,得到的便是相对滑板的向心力FN。实际上P刚要脱离滑板时,与滑板在水平方向的速度一样,而在竖直方向的速度为v2。此时,P与滑板之间在水平方向相对速度为零,但滑板受到P水平向左的压力,滑板具有加速度,因此P与滑板相对加速度并不等于零,滑板为非惯性系,即P在圆轨道BC上运动的对地轨迹不是圆弧,⑤式有误。
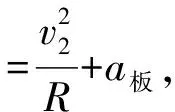
一题多解是物理教学中常用的教学手段,旨在通过对方法合理性的判断、对方法便捷性的对比、对方法适用性的反思来拓宽解题思路,进而提高学生的科学思维能力。例2在非惯性系中应如何求解呢?
【解法1】以滑板为参考系,要考虑惯性力。
方程①②③④式如原解析,接下来的解答如下:

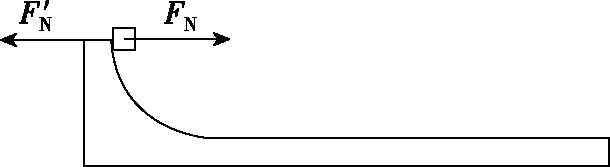
图5
【评析】显然,此解法比较便捷,有利于拓宽优生的解题思路,培养科学思维,落实学科核心素养。但惯性力对大部分学生还是比较抽象难懂,只有极小部分的竞赛生才会涉及。还可以以圆周运动为参考系,要考虑科氏力,但科氏力在竖直方向,对向心力的求解无影响,考虑到解题过程与解法1十分相似,这里不再赘述。
【解法2】以地面为参考系,要考虑相对加速度。
方程①②③④式如原解析,接下来的解答如下:
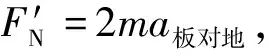
【评析】解法2从相对运动的角度巧妙地规避了惯性力,创新性地解决问题,有利于优生地选拔和培养。
类似的题型在2022年全国物理竞赛预赛中出现过,其第3题就是需要按这一思路求解。
【例3】(2022年全国物理竞赛预赛第3题)三个质量皆为m的小球a、b、c由三段长度皆为l的不可伸长的轻细线L1、L2、L3相继连接,竖直悬挂,并处于静止状态,如图6所示。在某一时刻,小球a、b受到水平方向的冲击,分别获得向右、向左的大小为v的速度。此时,中间那段细线L2的张力大小为

图6
( )
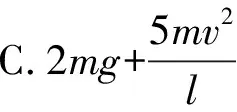
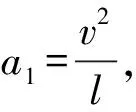
【评析】教学中,针对不同生源,我们应选择不同的教学素材,实行分层教学,进而达到精准培育的目标。此题与前面两道例题相比,由两个研究对象升级为三个研究对象,由一段轻绳增加到三段,难度陡增,达到了进一步提升学生关键能力的目的。
一题多变是习题教学中学生全方位掌握知识的有效途径之一,在实际教学中应尽量避免超纲现象,考虑到惯性力有超纲的嫌疑,不妨将例2稍加改造。
【拓展2】把例2所求问题改为物块P返回B处时受到的作用力FN多大?
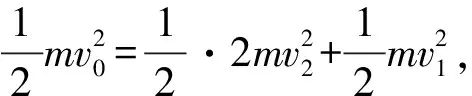
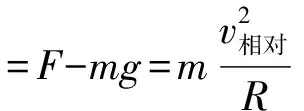
4 结束语
综上所述,惯性系中的相对圆周运动,求解向心力时无需考虑惯性力。非惯性系中的相对圆周运动,求解向心力时是否需要考虑惯性力,取决于惯性力对所求物理量是否有影响。只有对相对圆周运动的向心力求解做系统深入的研究,才能有效规避科学性错误。教学中应多维度地提升学生的物理思维品质,避免仅用靠“刷题”来提升解题能力,有效地减轻了学生课业负担,落实了新课标中的“转变教学方式、提倡教学方式多样化”的新理念。
