形似质异难辨析 物含妙理总堪寻——例谈电磁感应现象中的安培力做功问题

许冬保

(江西省九江第一中学)

在电磁感应现象中,存在着发电机中的电动机效应以及电动机中的发电机效应,这涉及对发电机模型及电动机模型的建构与认知。其中,安培力做功问题,在学生中有着多方面的困惑,发电机与电动机模型形似质异,如何辨析?值得堪寻。

1 发电机模型与电动机模型

在电磁感应现象中,安培力既可以做负功,也可以做正功,前者对应发电机模型,后者对应电动机模型。以下讨论直流发电机与直流电动机的简化模型,分析中不计电磁辐射及导轨自身电阻引起的能量损失。

1.1 直流发电机简化模型及其分析

如图1为简化的直流发电机模型,足够长的光滑导轨上放有一金属导体棒,导轨左侧连接电阻R,导体棒的电阻为r。闭合开关S,同时给导体棒施加水平向右的恒力作用,使导体棒开始运动,稳定后导体棒以速度v0做匀速运动。在该过程中,安培力做负功,使机械能减少,电能增加。

图1

1.1.1 微观分析

金属导体棒中的载流子为自由电子(以下简称电子),设电子的电荷量为e,闭合开关S,达到稳定状态时,导体棒中的电子随棒平动的速度为v0,其受到的洛伦兹力为f1=eBv0,方向如图2所示。在f1作用下,电子相对导体棒定向移动,设移动速率为vy,则以该速率运动的电子也受到洛伦兹力f2=eBvy作用,方向与v0方向相反。

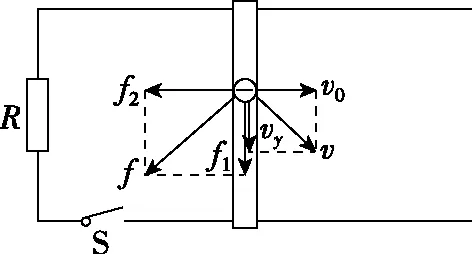
图2

图2表明:电子受到两个洛伦兹力作用。其中,f1做正功,在一段极短时间Δt内,有W1=f1vyΔt=eBvyv0Δt;f2做负功,在相同的一段极短时间Δt内,有W2=-f2v0Δt=-eBvyv0Δt。可见,W1+W2=0,即洛伦兹力的两个分力做功的代数和为零。因此,f1、f2的合力f的方向与v0、vy的合速度v的方向一定相互垂直。

由于导体棒两端有电荷积累,因此,导体棒就相当于一个电源。设ab两端电压为U,导体棒有效长度为l,若棒中正离子对电子的平均阻力为f0,则由平衡条件,有

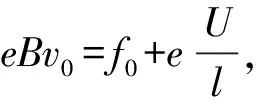
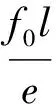
1.1.2 宏观分析

如上所述,f1使电子相对导体棒定向迁移,宏观上表现为“非静电力”作用,导体棒相当于电源,将电子由棒的a端移到b端,非静电力所做的功为W非=eBv0·l,由电动势的定义,有

该电动势即为动生电动势,所得结果与微观分析一致。

1.2 直流电动机简化模型及其分析

图3

1.2.1 微观分析

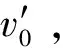
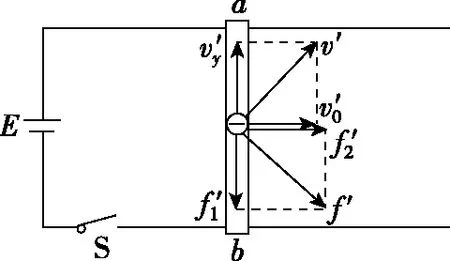
图4

设导体棒ab两端电压为U,导体棒有效长度为l,棒中正离子对电子的平均阻力为f0,则由平衡条件,有

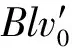
1.2.2 宏观分析

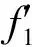
“反电动势”反映电动机中的发电机效应,所得结果与微观分析一致。

2 问题分析

关于发电机与电动机的教学要求,《普通高中物理课程标准》(简称“课标”)指出:“了解发电机和电动机工作过程中的能量转化。认识电磁学在人类生活和社会发展中的作用”。对于反电动势,“课标”未作要求,教材上的介绍比较简洁。有鉴于此,以下实例主要是对直流发电机模型进行分析。

2.1 直流发电机模型(单棒运动)

【例1】如图5,固定于水平面的U形导线框处于竖直向下的匀强磁场中,金属直导线MN在与其垂直的水平恒力F作用下,在导线框上以速度v做匀速运动,速度v与恒力F方向相同;导线MN始终与导线框形成闭合电路。已知导线MN电阻为R,其长度L恰好等于平行轨道间距,磁场的磁感应强度为B。忽略摩擦阻力和导线框的电阻。

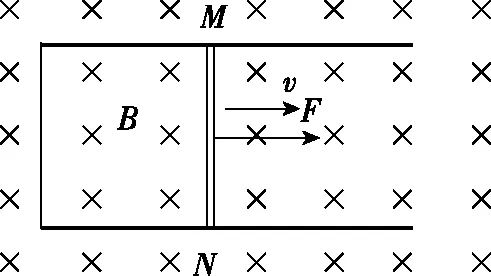
图5

(1)通过公式推导验证:在Δt时间内,F对导线MN所做的功W等于电路获得的电能W电,也等于导线MN中产生的焦耳热Q;

【解析】(1)金属直导线MN产生的动生电动势为E=BLv

导线匀速运动,由平衡条件,有F=F安=ILB

在Δt时间内,外力F对导线所做的功为

W=F·vΔt

即W=ILB·vΔt=BLv·IΔt=BLv·q

电路获得的电能

W电=qE=IEΔt=IBLv·Δt=BLv·q

可见,F对导线MN做的功等于电路获得的电能W电

导线MN中产生的热量

Q=I2RΔt=IΔt·IR=qE=W电

因此,电路获得的电能W电等于导线MN中产生的焦耳热Q。

(2)由于回路中的电流保持不变,因此,从微观上分析知,电子相对导线做匀速直线运动。

【评述】导体切割磁感线的运动可以从宏观和微观两个视角来认识。根据能量守恒定律可知,克服安培力所做的功等于电路获得的电能。对于纯电阻电路,电能全部转化为焦耳热。关于电子定向运动中受到的平均阻力还可以由能量、动量观点来处理。

2.2 直流发电机模型(双棒运动)

【例2】如图6,在两光滑水平金属导轨上静止放置a、b两根导体棒,整个装置处于竖直向下的匀强磁场中。用水平恒力F拉动a棒,在运动过程中,a、b棒始终与导轨接触良好,若不计导轨电阻。下列说法正确的是

图6

( )

A.拉力F做的功等于a、b棒增加的动能与a、b棒中产生的焦耳热之和

B.安培力对b做的功等于b棒增加的动能与b棒中产生的焦耳热之和

C.安培力对a、b棒做功的代数和的绝对值小于a、b棒中产生的焦耳热之和

D.a棒克服安培力做功等于b棒增加的动能与a、b棒中产生的焦耳热之和

【解析】在拉力F作用下,a棒产生动生电动势,闭合电路中形成逆时针方向的感应电流。a棒所受安培力FBa方向与F反向,水平向左;b棒所受安培力FBb方向水平向右。研究a、b棒组成的系统,某一时刻,由功能关系,有WF=Eka+Ekb+Qa+Qb。式中,Eka、Ekb分别为某一时刻a、b棒的动能;Qa、Qb分别为该过程a、b棒产生的焦耳热。设安培力在一段时间内,对a、b棒做的功分别为Wa、Wb。对b棒,安培力FBb做正功,由动能定理,有Wb=Ekb。对a棒,安培力FBa做负功,由动能定理,有WF+Wa=Eka。安培力对a、b棒做功的代数和Wa+Wb=-(Qa+Qb),即|Wa+Wb|=Qa+Qb。因此,a棒克服安培力做的功|Wa|=WF-Eka=Ekb+Qa+Qb。综上,正确选项为AD。

2.3 直流发电机模型(动生电动势与感生电动势并存)

【例3】如图7,两根平行金属导轨固定在水平桌面上,每根导轨单位长度的电阻为r0,导轨的端点P、Q用电阻可以忽略的导线相连,两导轨间的距离l。有随时间变化的匀强磁场垂直于桌面,已知磁感应强度B与时间t的关系为B=kt,比例系数k为常量(k>0)。一电阻不计的金属杆可在导轨上无摩擦地滑动,在滑动过程中保持与导轨垂直。在t=0时刻,金属杆紧靠在P、Q端,在外力作用下,杆以恒定的速度v从静止开始向导轨的另一端滑动,求经过时间t克服安培力所做的功及回路产生的焦耳热。

图7

【解析】分析可知,无论磁场方向是垂直纸面向里,还是向外,动生电动势与感生电动势的方向总是相同的。

设回路中的总电动势为E,经过时间t,金属杆与初始位置的距离L=vt,此时杆与导轨构成的回路的面积S=Ll,相应的总电阻R=2Lr0

由法拉第电磁感应定律,有

作用于杆的安培力F=BlI

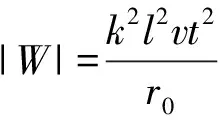
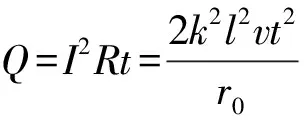
【评述】该题中克服安培力所做的功等于回路中产生的焦耳热的一半。其原因是,安培力做功与感生电动势的存在与否无关,只与动生电动势有关。

2.4 直流发电机模型(含有电容器元件)

【例4】足够长的光滑平行金属导轨固定在绝缘水平面上,导轨左端连接电容为C的电容器,导轨间距为l,磁感应强度大小为B、方向竖直向下的匀强磁场穿过导轨所在平面。一质量为m的导体棒垂直静置在导轨上,如图8所示。t=0时刻导体棒在水平拉力作用下从静止开始向右运动,电容器两极板间电势差U随时间t变化的图像如图9所示,不计导轨及导体棒电阻,则

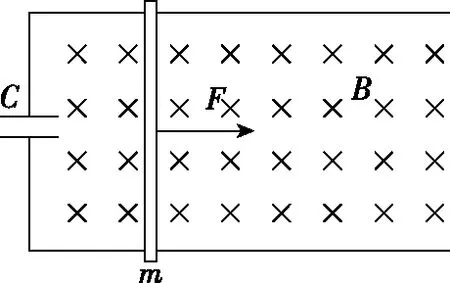
图8

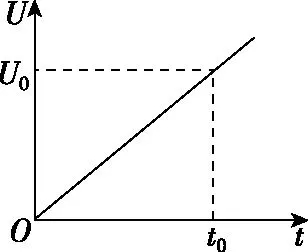
图9

( )

【评述】克服安培力做功,使其他形式的能量减少,电容器储存的电场能增加。若回路存在电阻,则还会产生焦耳热。关于电场能也可以按以下方法来处理。

2.5 直流电动机模型

【例5】如图10,电源的电动势为1.50 V,内电阻0.50 Ω;金属导轨间距0.50 m,导体AB杆电阻为0.10 Ω,导轨的电阻不计。磁感应强度为0.50 T,金属导轨对AB杆的滑动摩擦力大小为0.25 N。解答以下问题:

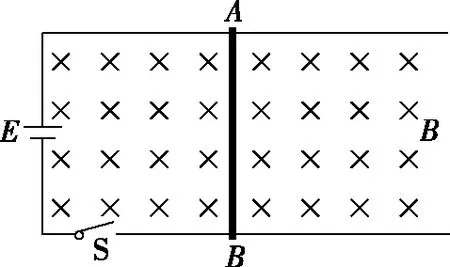
图10

(1)分析一下,当开关S闭合后,会发生哪些电磁现象;

(2)当AB杆的速度达到稳定时(即速度最大时),电路中的电流多大;

(3)AB杆的最大速度;

(4)稳定状态时电源消耗的电能转化为什么形式的能?通过计算验证一下:能的转化是否符合守恒定律。

【解析】(1)当开关S闭合后,会发生如下一些电磁现象:其一是闭合电路中的电流在周围空间激发磁场;其二是AB杆通电在磁场中受到安培力作用,其方向水平向右;其三是当AB杆开始运动后,因切割磁感线而在其上产生动生电动势,它的方向与AB杆中电流的方向相反。

因此,可得

(4)稳定状态时电源消耗的电能一部分转化为电路中的内能,使电阻发热;另一部分通过导体克服摩擦力作功转化为内能。注意这时AB杆速度达到稳定,导体AB杆的动能无变化。

电源消耗的功率

P=IE=1.00×1.50 W=1.50 W

AB杆克服摩擦力做功而消耗的功率

P′=Ff·v=0.25×3.60 W=0.90 W

电路中电阻上消耗的功率为

P热=I2(R+r)=1.002×(0.10+0.50)W=0.60 W

根据计算可知,P=P′+P热,符合能的转化与守恒定律。

【评述】该例源于早期人教社出版的甲种本物理教材第三册上的习题。从解析中可以发现,该题重视物理现象的分析,强化基础知识的理解,凸显思维方法的应用,渗透能量观念分析问题。今天看来仍具有重要的价值,与物理核心素养的理念是一脉相承的。安培力做功的功率即安培力做功的快慢,本例题在稳定状态时安培力做功的功率等于克服摩擦力做功的功率;若考查从初始状态至稳定状态的过程,则安培力所做的功等于AB杆增加的机械能及因摩擦产生的内能之和。